СП 52-102-2004 Предварительно напряженные железобетонные конструкции
Система нормативных документов в строительстве
СВОД ПРАВИЛ ПО ПРОЕКТИРОВАНИЮ И СТРОИТЕЛЬСТВУ
ПРЕДВАРИТЕЛЬНО НАПРЯЖЕННЫЕ ЖЕЛЕЗОБЕТОННЫЕ КОНСТРУКЦИИ
СП 52-102-2004
ПРЕДИСЛОВИЕ
1 РАЗРАБОТАН Научно-исследовательским, проектно-конструкторским и технологическим институтом бетона и железобетона (ГУН «НИИЖБ») Госстроя России
ВНЕСЕН Управлением технического нормирования, стандартизации и сертификации в строительстве и ЖКХ Госстроя России
2 ОДОБРЕН И РЕКОМЕНДОВАН для применения письмом Госстроя России от 24.05.2004 № ЛБ-473/9
3 ВВЕДЕН ВПЕРВЫЕ
Оглавление
|
Введение 1 Общие указания 1.1 Основные положения 1.2 Основные расчетные требования 2 Материалы для предварительно напряженных железобетонных конструкций 2.1 Бетон 2.1.1 Показатели качества бетона и их применение при проектировании 2.1.2 Нормативные и расчетные значения характеристик бетона 2.2 Арматура 2.2.1 Показатели качества арматуры 2.2.2 Нормативные и расчетные значения характеристик арматуры 2.2.3 Предварительные напряжения арматуры 3 Расчет элементов предварительно напряженных железобетонных конструкций по предельным состояниям первой группы 3.1 Расчет предварительно напряженных железобетонных элементов по прочности 3.1.1 Общие положения 3.1.2 Расчет предварительно напряженных элементов на действие изгибающих моментов в стадии эксплуатации но предельным усилиям 3.1.3 Расчет предварительно напряженных элементов в стадии предварительного обжатия 3.1.4 Расчет по прочности нормальных сечений на основе нелинейной деформационной модели 3.1.5 Расчет предварительно напряженных элементов при действии поперечных сил 4 Расчет предварительно напряженных элементов железобетонных конструкций по предельным состояниям второй группы 4.1 Общие положения 4.2 Расчет предварительно напряженных железобетонных элементов по раскрытию трещин 4.2.1 Общие положения 4.2.2 Определение момента образования трещин, нормальных к продольной оси элемента 4.2.3 Расчет ширины раскрытия трещин, нормальных к продольной оси элемента 4.3 Расчет предварительно напряженных железобетонных элементов по деформациям 4.3.1 Общие положения 4.3.2 Расчет предварительно напряженных элементов по прогибам 4.3.3 Определение кривизны изгибаемых предварительно напряженных элементов 4.3.4 Определение кривизны предварительно напряженных элементов на основе нелинейной деформационной модели 5 Конструктивные требования 5.1 Общие положения 5.2 Защитный слой бетона 5.3 Анкеровка арматуры Приложение А Основные буквенные обозначения Приложение Б Перечень нормативных документов, на которые даны ссылки в тексте
|
В ведение
Настоящий Свод правил разработан в развитие СНиП 52-01-2003 «Бетонные и железобетонные конструкции. Основные положения».
Свод правил содержит рекомендации по расчету и проектированию предварительно напряженных железобетонных конструкций промышленных и гражданских зданий и сооружений из тяжелого бетона, которые обеспечивают выполнение обязательных требований СНиП 52-01-2003.
Решение вопроса о применении Свода правил при проектировании предварительно напряженных железобетонных конструкций конкретных зданий и сооружений относится к компетенции заказчика или проектной организации. В случае если принято решение о применении настоящего Свода правил, должны быть выполнены все установленные в нем требования.
В Своде правил не приведены особенности расчета и проектирования предварительно напряженных конструкций, подвергаемых циклическим и динамическим воздействиям, воздействиям высоких температур и агрессивных сред. Эти особенности, а также более детальные положения по расчету линейных железобетонных систем и плоских и пространственных железобетонных конструкций освещены в соответствующих сводах правил.
Настоящий Свод правил следует применять совместно с СП 52-101-2003 «Бетонные и железобетонные конструкции без предварительного напряжения арматуры».
Единицы физических величин, приведенные в Своде правил: сила выражена в ньютонах (Н) или в килоньютонах (кН); линейные размеры - в мм (для сечений) или в м (для элементов или их участков); напряжения, сопротивления, модули упругости - в мегапаскалях (МПа); распределенные нагрузки и усилия - в кН/м или Н/мм.
Свод правил разработали доктора технических наук А.С. Залесов, А.И. Звездов, ТА. Мухамедиев, Е.АЛистяков (ГУП «НИИЖБ» Госстроя России).
СВОД ПРАВИЛ ПО ПРОЕКТИРОВАНИЮ И СТРОИТЕЛЬСТВУ
ПРЕДВАРИТЕЛЬНО НАПРЯЖЕННЫЕ ЖЕЛЕЗОБЕТОННЫЕКОНСТРУКЦИИPRESTRESSED CONCRETE STRUCTURES |
1 о бщие указания
1.1 Основные положения
1.1.1 Рекомендации настоящего Свода правил (СП) распространяются на проектирование предварительно напряженных железобетонных конструкций промышленных и гражданских зданий и сооружений, выполненных из тяжелого бетона классов по прочности на сжатие от В20 до В60 с натяжением арматуры до твердения бетона (на упоры) и эксплуатируемых в климатических условиях России, в среде с неагрессивной степенью воздействия, при статическом действии нагрузки.
Рекомендации СП не распространяются на проектирование предварительно напряженных железобетонных конструкций гидротехнических сооружений, мостов, покрытий автомобильных дорог и аэродромов и других специальных сооружений.
1.1.2 Предварительно напряженные железобетонные конструкции должны быть обеспечены с требуемой надежностью от возникновения всех видов предельных состояний расчетом, выбором показателей качества материалов, назначением размеров и конструированием согласно указаниям настоящего СП. При этом должны быть выполнены технологические требования при изготовлении конструкций и соблюдены требования по эксплуатации зданий и сооружений, а также требования по экологии, устанавливаемые соответствующими нормативными документами.
1.2 Основные расчетные требования
1.2.1 Расчеты предварительно напряженных железобетонных конструкций следует производить по предельным состояниям, включающим:
- предельные состояния первой группы (по полной непригодности к эксплуатации вследствие потери несущей способности);
- предельные состояния второй группы (по непригодности к нормальной эксплуатации вследствие образования или чрезмерного раскрытия трещин, появления недопустимых деформаций и др.).
Расчеты по предельным состояниям первой группы, содержащиеся в настоящем СП, включают расчет по прочности.
Расчеты по предельным состояниям второй группы, содержащиеся в настоящем СП, включают расчеты по раскрытию трещин и по деформациям.
1.2.2 Расчет по предельным состояниям конструкции в целом, а также отдельных ее элементов следует, как правило, производить для всех стадий - изготовления, транспортирования, возведения и эксплуатации; при этом расчетные схемы должны отвечать принятым конструктивным решениям.
1.2.3 Расчеты предварительно напряженных железобетонных конструкций необходимо, как правило, производить с учетом возможного образования трещин и неупругих деформаций в бетоне и арматуре.
Определение усилий и деформаций от различных воздействий в конструкциях и в образуемых ими системах зданий и сооружений следует производить по методам строительной механики, как правило, с учетом физической и геометрической нелинейности работы конструкций.
1.2.4 При проектировании предварительно напряженных железобетонных конструкций надежность конструкций устанавливают расчетом путем использования расчетных значений нагрузок и воздействий, расчетных значений характеристик материалов, определяемых с помощью соответствующих частных коэффициентов надежности по нормативным значениям этих характеристик с учетом степени ответственности зданий и сооружений.
Нормативные значения нагрузок и воздействий, коэффициентов сочетаний, коэффициентов надежности по нагрузке, коэффициентов надежности по назначению конструкций, а также подразделение нагрузок на постоянные и временные (длительные и кратковременные) принимают согласно СНиП 2.01.07.
1.2.5 При расчете элементов сборных конструкций на воздействие усилий, возникающих при их подъеме, транспортировании и монтаже, нагрузку от всех элементов следует принимать с коэффициентом динамичности, равным: 1,60 - при транспортировании; 1,40 - при подъеме и монтаже. Допускается принимать более низкие, обоснованные в установленном порядке, значения коэффициентов динамичности, но не ниже 1,25.
2 м атериалы для предварительно напряженных железобетонных конструкций
2.1 Бетон
2.1.1 Показатели качества бетона и их применение при проектировании
2.1.1.1 Для предварительно напряженных железобетонных конструкций, проектируемых в соответствии с требованиями настоящего СП, следует предусматривать конструкционный тяжелый бетон средней плотности от 2200 кг/м3 до 2500 кг/м3 включительно.
2.1.1.2 Основными показателями качества бетона, устанавливаемыми при проектировании, являются:
а) класс по прочности на сжатие В;
б) класс по прочности на осевое растяжение Bt (назначают в случаях, когда эта характеристика имеет главенствующее значение и ее контролируют на производстве);
в) марка по морозостойкости F (назначают для конструкций, подвергаемых действию попеременного замораживания и оттаивания);
г) марка по водонепроницаемости W (назначают для конструкций, к которым предъявляют требования ограничения водопроницаемости).
Классы бетона по прочности на сжатие В и осевое растяжение Bt отвечают значению гарантированной прочности бетона (МПа) с обеспеченностью 0,95.
2.1.1.3 Для предварительно напряженных железобетонных конструкций следует предусматривать бетоны следующих классов и марок:
а) классов по прочности на сжатие:
В20; В25; В30; В35; В40; В45; В50; В55; В60;
б) классов по прочности на осевое растяжение:
Bt0,8; Btl,2; Bt1,6; Bt2,0; Bt2,4; Bt2,8; Bt3,2;
в) марок по морозостойкости:
F50; F75; F100; F150; F200; F300; F400; F500;
г) марок по водонепроницаемости: W 2; W 4; W 6; W 8; W 10; W 12.
2.1.1.4 Возраст бетона, отвечающий его классу по прочности на сжатие и осевое растяжение (проектный возраст), назначают при проектировании исходя из возможных реальных сроков загружения конструкций проектными нагрузками. При отсутствии этих данных класс бетона устанавливают в возрасте 28 суток.
2.1.1.5 Для предварительно напряженных конструкций рекомендуется применять класс бетона по прочности на сжатие в зависимости от класса напрягаемой арматуры, но не ниже В20.
Передаточную прочность бетона Rbp (прочность бетона к моменту его обжатия, контролируемая аналогично классу бетона по прочности на сжатие) следует назначать не менее 15 МПа и не менее 50 % принятого класса бетона по прочности на сжатие.
2.1.1.6 Марку бетона по морозостойкости назначают в зависимости от требований, предъявляемых к конструкциям, режима их эксплуатации и условий окружающей среды.
Для надземных конструкций, подвергаемых атмосферным воздействиям окружающей среды при расчетной отрицательной температуре наружного воздуха в холодный период от минус 5 °С до минус 40 °С, принимают марку бетона по морозостойкости не ниже F 75, а при расчетной температуре наружного воздуха выше минус 5 °С в указанных выше конструкциях марку бетона по морозостойкости не нормируют.
В остальных случаях требуемые марки бетона по морозостойкости устанавливают в зависимости от назначения конструкций и условий окружающей среды по специальным указаниям.
2.1.1.7 Марку бетона по водонепроницаемости назначают в зависимости от требований, предъявляемых к конструкциям, режима их эксплуатации и условий окружающей среды.
Для надземных конструкций, подвергаемых атмосферным воздействиям при расчетной отрицательной температуре наружного воздуха выше минус 40 °С, а также для наружных стен отапливаемых зданий марку бетона по водонепроницаемости не нормируют.
В остальных случаях требуемые марки бетона по водонепроницаемости устанавливают по специальным указаниям.
2.1.2 Нормативные и расчетные значения характеристик бетона
Нормативные значения прочностных характеристик, бетона
2.1.2.1 Основными прочностными характеристиками бетона являются нормативные значения:
- сопротивления бетона осевому сжатию Rb , n ;
- сопротивления бетона осевому растяжению Rbt , n .
Нормативные значения сопротивления бетона осевому сжатию (призменная прочность) и осевому растяжению (при назначении класса бетона по прочности на сжатие) принимают в зависимости от класса бетона по прочности на сжатие В согласно таблице 1.
При назначении класса бетона по прочности на осевое растяжение Bt нормативные значения сопротивления бетона осевому растяжению Rbt , n принимают равными числовой характеристике класса бетона на осевое растяжение.
Расчетные значения прочностных характеристик бетона
2.1.2.2 Расчетные значения сопротивления бетона осевому сжатию Rb и осевому растяже нию Rbt определяют по формулам:
![]() ; (1)
; (1)
![]() . (2)
. (2)
Значения коэффициента надежности по бетону при сжатии γ b принимают равными:
1,3 - для предельных состояний по несу щей способности (первая группа);
1,0 - для предельных состояний по эксп луатационной пригодности (вторая группа).
Значения коэффициента надежности по бе тону при растяжении γ bt принимают равными:
1,5 - для предельных состояний по несущей способности при назначении класса бето на по прочности на сжатие;
1,3 - для предельных состояний по несу щей способности при назначении класса бето на по прочности на осевое растяжение;
1,0 - для предельных состояний по эксп луатационной пригодности.
Расчетные значения сопротивления бетона Rb , Rbt , Rb , ser , Rbt , ser ( c округлением) в зависимос ти от класса бетона по прочности на сжатие и осевое растяжение приведены: для предельных состояний первой группы в таблицах 2 и 3, вто рой группы - в таблице 1.
Таблица 1
|
Вид сопротивления |
Нормативные значения сопротивления бетона Rb , n и Rbt , n и расчетные значения сопротивления бетона для предельных состояний второй группы Rb , ser и Rbt , ser , МПа, при классе бетона по прочности на сжатие |
|||||||||
|
В15 |
В20 |
В25 |
В30 |
В35 |
В40 |
B 45 |
В50 |
В55 |
В60 |
|
|
Сжатие осевое (призменная прочность) Rb,n , Rb,ser |
11,0 |
15,0 |
18,5 |
22,0 |
25,5 |
29,0 |
32,0 |
36,0 |
39,5 |
43,0 |
|
Растяжение осевое Rbt , n , Rbt , ser |
1,1 |
1,35 |
1,55 |
1,75 |
1,95 |
2,1 |
2,25 |
2,45 |
2,6 |
2,75 |
Таблица 2
|
Вид сопротивления |
Расчетные значения сопротивления бетона для предельных состояний первой группы Rb и Rbt , МПа, при классе бетона по прочности на сжатие |
|||||||||
|
В15 |
В20 |
В25 |
В30 |
В35 |
В40 |
В45 |
В50 |
В55 |
В60 |
|
|
Сжатие осевое (призменная прочность) Rb |
8,5 |
11,5 |
14,5 |
17,0 |
19,5 |
22,0 |
25,0 |
27,5 |
30,0 |
33,0 |
|
Растяжение осевое Rbt |
0,75 |
0,9 |
1,05 |
1,15 |
1,3 |
1,4 |
1,5 |
1,6 |
1,7 |
1,8 |
Таблица 3
|
Вид сопротивления |
Расчетные значения сопротивления бетона для предельных состояний первой группы Rbt МПа, при классе бетона по прочности на осевое растяжение |
||||||
|
В t 0,8 |
Bt1,2 |
В t 1,6 |
В t 2,0 |
В t 2,4 |
В t 2,8 |
В t 3,2 |
|
|
Растяжение осевое Rbl |
0,62 |
0,93 |
1,25 |
1,55 |
1,85 |
2,15 |
2,45 |
2.1.2.3 В необходимых случаях расчетные зна чения прочностных характеристик бетона ум ножают на коэффициенты условий работы γ bi учитывающие особенности работы бетона в кон струкции (характер нагрузки, условия окружа ющей среды и т.д.).
Влияние длительности действия статическ ой нагрузки учитывается коэффициентом ус ловий работы бетона γ b 1 , вводимым к расчет ным значениям сопротивлений Rb и Rbt и при нимаемым равным:
γ b 1 = 1,0 - при непродолжительном (крат ковременном) действии нагрузки;
γ b 1 = 0,9 - при продолжительном (длитель ном) действии нагрузки.
Влияние попеременного замораживания и оттаивания, а также отрицательных темпера тур учитывают коэффициентом условий рабо ты бетона γ b 4 ≤ 1,0. Для надземных конструк ций, подвергаемых атмосферным воздействи ям окружающей среды при расчетной темпера туре наружного воздуха в холодный период минус 40 °С и выше, принимают коэффициент γ b 4 = 1,0. В остальных случаях значения коэффи циента γ b 4 принимают в зависимости от назна чения конструкции и условий окружающей сре ды согласно специальным указаниям.
Деформационные характеристики бетона
2.1.2.4 Основными деформационными характеристиками бетона являются значения:
- предельных относительных деформаций бетона при осевом сжатии и растяжении (при однородном напряженном состоянии бетона) ε b 0 и ε bt 0 ;
- начального модуля упругости Е b ;
- коэффициента (характеристики) ползучести φ b , cr ;
- коэффициента поперечной деформации бетона (коэффициента Пуассона) νb , P ;
- коэффициента линейной температурной деформации бетона α bt .
2.1.2.5 Значения предельных относительных деформаций бетона принимают равными:
при непродолжительном действии нагрузки
ε b 0 = 0,002 - при осевом сжатии;
ε bt 0 = 0,0001 - при осевом растяжении;
при продолжительном действии нагрузки - по таблице 6 в зависимости от относительной влажности окружающей среды.
2.1.2.6 Значения начального модуля упругости бетона при сжатии и растяжении принимают в зависимости от класса бетона по прочности на сжатие В согласно таблице 4.
Таблица 4
|
Значения начального модуля упругости бетона при сжатии и растяжении Е b , МПа·10-3, при классе бетона по прочности на сжатие |
|||||||||
|
В15 |
В20 |
В25 |
В30 |
В35 |
В40 |
В45 |
В50 |
В55 |
В60 |
|
24,0 |
27,5 |
30,0 |
32,5 |
34,5 |
36,0 |
37,0 |
38,0 |
39,0 |
39,5 |
При продолжительном действии нагрузки значения начального модуля деформаций бетона определяют по формуле
![]() , (3)
, (3)
где φ b , cr - коэффициент ползучести, принимаемый согласно п. 2.1.2.7.
2.1.2.7 Значения коэффициента ползучести бетона φ b , cr принимают в зависимости от условий окружающей среды (относительной влажности воздуха) и класса бетона. Значения коэффициента ползучести бетона приведены в таблице 5.
Таблица 5
|
Относительная влажность воздуха окружающей среды, % |
Значения коэффициента ползучести φ b , cr при классе бетона на сжатие |
|||||||||
|
В15 |
В20 |
В25 |
В30 |
В35 |
В40 |
В45 |
В50 |
В55 |
В60 |
|
|
Выше 75 |
2,4 |
2,0 |
1,8 |
1,6 |
1,5 |
1,4 |
1,3 |
1,2 |
1,1 |
1,0 |
|
40 - 75 |
3,4 |
2,8 |
2,5 |
2,3 |
2,1 |
1,9 |
1,8 |
1,6 |
1,5 |
1,4 |
|
Ниже 40 |
4,8 |
4,0 |
3,6 |
3,2 |
3,0 |
2,8 |
2,6 |
2,4 |
2,2 |
2,0 |
|
Примечание - Относительную влажность воздуха окружающей среды принимают по СНиП 23-01 как среднюю месячную относительную влажность наиболее теплого месяца для района строительства. |
||||||||||
2.1.2.8 Значение коэффициента поперечной деформации бетона допускается принимать νb ,Р = 0,2.
2.1.2.9 Значение коэффициента линейной температурной деформации бетона при изменении температуры от минус 40 °С до плюс 50 °С принимают αbt = 1·10-5 °С-1.
Диаграммы состояния бетона
2.1.2.10 В качестве расчетных диаграмм со стояния бетона, определяющих связь между напряжениями и относительными деформаци ями, принимают трех- и двухлинейную диаг раммы (рисунок 1).
Диаграммы состояния бетона используют при расчете железобетонных элементов по не линейной деформационной модели.
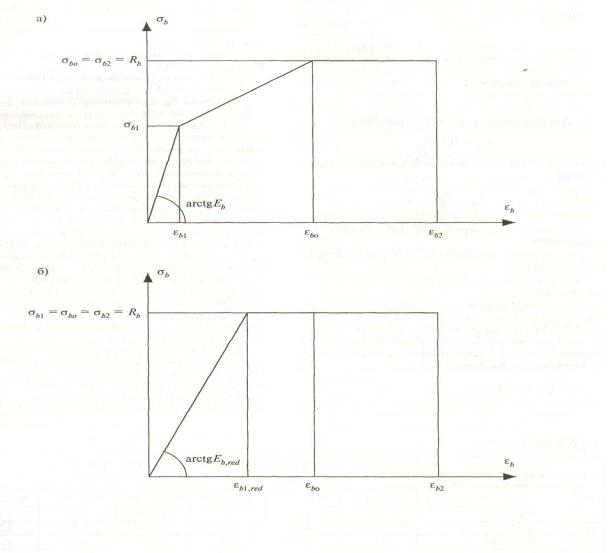
а – трехлинейная; б – двухлинейная
Рисунок 1 – Диаграммы состояния сжатого бетона
2.1.2.11 При трехлинейной диаграмме (рисунок 1, а) сжимающие напряжения бетона σ b в зависимости от относительных деформаций укорочения бетона ε b определяют по формулам:
при 0 ≤ ε b ≤ ε b 1
σb =Е b εb , (4)
при ε b 1 < ε b < ε b 0
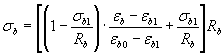 ; (5)
; (5)
при ε b 0 ≤ ε b ≤ ε b 2
σb = Rb (6)
Значения напряжений σb 1 принимают:
σb 1 = 0,6 Rb ,
а значения относительных деформаций ε b 1 принимают:
![]() .
.
Значения относительных деформаций ε b 2 принимают:
при непродолжительном действии нагрузки ε b 2 = 0,0035;
при продолжительном действии нагрузки - по таблице 6.
Значения Rb , Eb и ε b 0 принимают согласно пп. 2.1.2.2, 2.1.2.3, 2.1.2.5, 2.1.2.6.
Таблица 6
|
Относительная влажность воздуха окружающей среды, % |
Относительные деформации бетона при продолжительном действии нагрузки |
|||||
|
при сжатии |
при растяжении |
|||||
|
ε b0 ·103 |
ε b2 ·103 |
ε b1,red ·103 |
ε bt0 ·103 |
ε bt2 ·103 |
ε bt1,red ·103 |
|
|
Выше 75 |
3,0 |
4,2 |
2,4 |
0,21 |
0,27 |
0,19 |
|
40-75 |
3,4 |
4,8 |
2,8 |
0,24 |
0,31 |
0,22 |
|
Ниже 40 |
4,0 |
5,6 |
3,4 |
0,28 |
0,36 |
0,26 |
|
Примечание — Относительную влажность воздуха окружающей среды принимают по СНиП 23-01 как среднюю месячную относительную влажность наиболее теплого месяца для района строительства. |
||||||
2.1.2.12 При двухлинейной диаграмме ( рисунок 1,б) сжимающие напряжения бетона σb в зависимости от относительных деформаций ε b 1 определяют по формулам:
при 0 ≤ ε b ≤ ε b 1, red
σb= Е b,red εb ; (7)
при ε b1,red ≤ ε b ≤ ε b2
σb = Rb . (8)
Значения приведенного модуля деформации бетона Е b , red принимают:
![]() . (9)
. (9)
Значения относительных деформаций ε b 1, red равны:
- при непродолжительном действии нагрузки ε b 1, red = 0,0015;
- при продолжительном действии нагрузки - по таблице 6.
Значения Rb , ε b 2 принимают как в п. 2.1.2.11, a Rb ,п - по таблице 1.
2.1.2.13 Растягивающие напряжения бетона σbt в зависимости от относительных деформаций ε bt определяют по диаграммам, приведенным на рисунке 1. При этом расчетные значения сопротивления бетона сжатию Rb заменяют на расчетные значения сопротивления бетона растяжению Rbt согласно пп. 2.1.2.2, 2.1.2.3; значения начального модуля упругости Е bt определяют согласно п. 2.1.2.6; значения относительной деформации ε bt 0 принимают согласно п. 2.1.2.5; значения относительной деформации ε bt 2 принимают при непродолжительном действии нагрузки ε bt 2 = 0,00015, при продолжительном действии нагрузки - по таблице 6. Для двухлинейной диаграммы принимают ε bt 1, red = 0,00008 - при непродолжительном действии нагрузки, а при продолжительном - по таблице 6; значения Ebt , red определяют по формуле (9), подставляя в нее Rbt , n и ε bt 1, red .
2.1.2.14 При расчете прочности железобетонных элементов по нелинейной деформационной модели для определения напряженно-деформированного состояния сжатой зоны бетона используют диаграммы состояния сжатого бетона, приведенные в пп. 2.1.2.11 и 2.1.2.12, с деформационными характеристиками, отвечающими непродолжительному действию нагрузки. При этом в качестве наиболее простой используют двухлинейную диаграмму состояния бетона.
2.1.2.15 При расчете образования трещин в железобетонных конструкциях по нелинейной деформационной модели для определения напряженно-деформированного состояния сжатого и растянутого бетона используют трехлинейную диаграмму состояния бетона, приведенную в пп. 2.1.2.11 и 2.1.2.13, с деформационными характеристиками, отвечающими непродолжительному действию нагрузки. Двухлинейную диаграмму ( пп. 2.1.2.12, 2.1.2.13) как наиболее простую используют для определения напряженно-деформированного состояния растянутого бетона при упругой работе сжатого бетона.
2.1.2.16 При расчете деформаций железобетонных элементов по нелинейной деформационной модели при отсутствии трещин для определения напряженно-деформированного состояния в сжатом и растянутом бетоне используют трехлинейную диаграмму состояния бетона с учетом непродолжительного и продолжительного действия нагрузки. При наличии трещин для определения напряженно-деформированного состояния сжатого бетона помимо указанной выше диаграммы используют, как наиболее простую, двухлинейную диаграмму состояния бетона с учетом непродолжительного и продолжительного действия нагрузки.
2.1.2.17 При расчете раскрытия нормальных трещин по нелинейной деформационной модели для определения напряженно-деформированного состояния в сжатом бетоне используют диаграммы состояния, приведенные в пп. 2.1.2.11 и 2.1.2.12, с учетом непродолжительного действия нагрузки. При этом в качестве наиболее простой используют двухлинейную диаграмму состояния бетона.
2.1.2.18 Влияние попеременного замораживания и оттаивания, а также отрицательных температур на деформационные характеристики бетона учитывают коэффициентом условий работы γ bt ≤ 1,0. Для надземных конструкций, подвергаемых атмосферным воздействиям окружающей среды при расчетной температуре наружного воздуха в холодный период минус 40 °С и выше, принимают коэффициент γ bt = 1,0. В остальных случаях значения коэффициента γ bt принимают в зависимости от назначения конструкций и условий окружающей среды.
2.2 Арматура
2.2.1 Показатели качества арматуры
2.2.1.1 Для армирования предварительно напряженных железобетонных конструкций следует применять отвечающую требованиям соответствующих государственных стандартов или утвержденных в установленном порядке технических условий арматуру следующих видов:
- горячекатаную гладкую и периодического профиля с постоянной и переменной высотой выступов (соответственно кольцевой и серповидный профили) диаметром 6 - 40 мм;
- термомеханически упрочненную периодического профиля с постоянной и переменной высотой выступов (соответственно кольцевой и серповидный профили) диаметром 6 - 40 мм;
- холоднодеформированную периодического профиля диаметром 3 - 12 мм;
- арматурные канаты диаметром 6 - 15 мм.
2.2.1.2 Основным показателем качества арматуры, устанавливаемым при проектировании, является класс арматуры по прочности на растяжение, обозначаемый:
А - для горячекатаной и термомеханически упрочненной арматуры;
Вр - для высокопрочной холоднодсформированной арматуры периодического профиля;
К - для арматурных канатов.
Классы арматуры по прочности на растяжение отвечают гарантированному значению предела текучести, физического или условного (равного значению напряжений, соответствующих остаточному относительному удлинению 0,2 %), с обеспеченностью не менее 0,95, определяемому по соответствующим стандартам.
Кроме того, в необходимых случаях к арматуре предъявляют требования по дополнительным показателям качества: свариваемость, пластичность, хладостойкость и др.
2.2.1.3 Для железобетонных конструкций, проектируемых в соответствии с требованиями настоящего СП, следует предусматривать:
в качестве напрягаемой арматуры:
горячекатаную и термомеханически упрочненную периодического профиля классов А600 (А- IV ), А800 ( A - V ) и А1000 (А- VI );
холоднодеформированную периодического профиля классов от Вр1200 до Вр1500 (Вр- II );
канатную 7- и 19-проволочную классов К1400, К1500 (К-7, К-19);
в качестве ненапрягаемой арматуры:
горячекатаную гладкую класса А 240 (А-1);
- горячекатаную, термомеханически упрочненную и холоднодеформированную периодического профиля классов А300 (А- II ), А400 (А- III ), А500 (А500С), В500 ( Bp - I , B 500 C ).
2.2.1.4 При выборе вида и марок стали для арматуры, устанавливаемой по расчету, а также прокатных сталей для закладных деталей следует учитывать температурные условия эксплуатации конструкций и характер их нагружения.
В конструкциях, эксплуатируемых при статической нагрузке в отапливаемых зданиях, а также на открытом воздухе и в неотапливаемых зданиях при расчетной температуре минус 40 °С и выше, может быть применена арматура всех вышеуказанных классов, за исключением арматуры класса А600 марки стали 80С (диаметром 10 - 18 мм), класса А300 марки стали Ст5пс (диаметром 18 - 40 мм) и класса А240 марки стали Ст3кп, которые применяют при расчетной температуре минус 30 °С и выше.
При других условиях эксплуатации класс арматуры и марку стали принимают по специальным указаниям.
При проектировании зоны передачи предварительного напряжения, анкеровки арматуры в бетоне и соединений арматуры внахлестку (без сварки) следует учитывать характер поверхности арматуры.
При проектировании сварных соединений арматуры следует учитывать способ изготовления арматуры ( ГОСТ 14098 ; РТМ 393 ).
2.2.1.5 Для монтажных (подъемных) петель элементов сборных железобетонных и бетонных конструкций следует применять горячекатаную арматурную сталь класса А240 марок Ст3сп и Ст3пс.
В случае если возможен монтаж конструкций при расчетной зимней температуре ниже минус 40 °С, для монтажных петель не допускается применять сталь марки Ст3пс.
2.2.2 Нормативные и расчетные значения характеристик арматуры
Нормативные значения прочностных характеристик арматуры
2.2.2.1 Основной прочностной характеристикой арматуры является нормативное значение сопротивления растяжению Rs , n , принимаемое в зависимости от класса арматуры по таблице 7.
Таблица 7
|
Класс арматуры |
Номинальный диаметр арматуры, мм |
Нормативные значения сопротивления растяжению Rs , n и расчетные значения сопротивления растяжению для предельных состояний второй группы Rs , ser , МПа |
|
А240 |
6-40 |
240 |
|
А300 |
6-40 |
300 |
|
А400 |
6-40 |
400 |
|
А500 |
10-40 |
500 |
|
А600 |
10-40 |
600 |
|
А800 |
10-32 |
800 |
|
А1000 |
10-32 |
1000 |
|
В500 |
3-12 |
500 |
|
Вр1200 |
8 |
1200 |
|
Вр1300 |
7 |
1300 |
|
Вр1400 |
4; 5; 6 |
1400 |
|
Вр1500 |
3 |
1500 |
|
К1400(К-7) |
15 |
1400 |
|
К1500(К-7) |
6; 9; 12 |
1500 |
|
К1500(К-19) |
14 |
1500 |
Расчетные значения прочностных характеристик арматуры
2.2.2.2 Расчетные значения сопротивления арматуры растяжению Rs определяют по формуле
![]() , (10)
, (10)
где γ s - коэффициент надежности по арматуре, принимаемый равным:
для предельных состояний первой группы:
1,1 - для арматуры классов А240, А300 и А400;
1,15 - для арматуры классов А300, А600 и А800;
1,2 - для арматуры классов А1000, В500, Bp 1200 – Bp 1500, K 1400, К1500;
для предельных состояний второй группы - 1,0.
Расчетные значения сопротивления арматуры растяжению Rs приведены (с округлением) для предельных состояний первой группы в таблице 8, второй группы - в таблице 7. При этом значения Rs , n - для предельных состояний первой группы приняты равными наименьшим контролируемым значениям по соответствующим ГОСТ.
Расчетные значения сопротивления арматуры сжатию Rsc принимают равными расчетным значениям сопротивления арматуры растяжению Rs , но не более значений, отвечающих деформациям укорочения бетона, окружающего сжатую арматуру: при кратковременном действии нагрузки - не более 400 МПа, при длительном действии нагрузки - не более 500 МПа. Для арматуры классов В500 и А600 граничные значения сопротивления сжатию принимаются с коэффициентом условий работы равным 0,9 (таблица 8).
Таблица 8
|
Класс арматуры |
Расчетные значения сопротивления арматуры для предельных состояний первой группы, МПа |
|
|
растяжению Rs |
сжатию Rsc |
|
|
А240 |
215 |
215 |
|
А300 |
270 |
270 |
|
А400 |
355 |
355 |
|
А500 |
435 |
435(400) |
|
А600 |
520 |
470(400) |
|
А800 |
695 |
500(400) |
|
А1000 |
830 |
500(400) |
|
В500 |
415 |
415(360) |
|
Вр1200 |
1000 |
500(400) |
|
Вр1300 |
1070 |
500(400) |
|
Вр1400 |
1170 |
500(400) |
|
Вр1500 |
1250 |
500(400) |
|
К1400 |
1170 |
500(400) |
|
К1500 |
1250 |
500(400) |
|
Примечание - Значения Rsc в скобках используют только при расчете на кратковременное действие нагрузки. |
||
2.2.2.3 В необходимых случаях расчетные значения прочностных характеристик арматуры умножают на коэффициенты условий работы γsi , учитывающие особенности работы арматуры в конструкции.
Расчетные значения сопротивления хомутов и отогнутой поперечной арматуры классов А600 - А1000, Вр1200 - Вр1500 и канатной Rsw принимают не более 0,8σ sp (с учетом всех потерь) и не более 300 МПа. В расчетах принимают большее из указанных значений. Расчетные значения Rsw для арматуры классов А240 - А500, В500 приведены в СП 52-101 .
Деформационные характеристики арматуры
2.2.2.4 Основными деформационными характеристиками арматуры являются значения:
относительных деформаций удлинения арматуры εs 0 при достижении напряжениями расчетного сопротивления Rs ;
модуля упругости арматуры Es .
2.2.2.5 Значения относительных деформаций арматуры εs 0 принимают равными:
для арматуры с физическим пределом текучести
![]() ; (11)
; (11)
для арматуры с условным пределом текучести
![]() . (12)
. (12)
2.2.2.6 Значения модуля упругости арматуры Es принимают одинаковыми при растяжении и сжатии и равными:
Es = 1,8-105 МПа - для арматурных канатов (К);
Es = 2,0-105 МПа - для остальной арматуры (А и В).
Диаграммы состояния арматуры
2.2.2.7 При расчете железобетонных элементов по нелинейной деформационной модели в качестве расчетной диаграммы состояния (деформирования) арматуры, устанавливающей связь между напряжениями σs и относительными деформациями εs арматуры, принимают для арматуры с физическим пределом текучести классов А240 - А500, В500 двухлинейную диаграмму (рисунок 2, а), а для арматуры с условным пределом текучести классов А600 - А1000, Вр1200 – Вр1500, К1400, К1500 - трехлинейную (рисунок 2, б).
Диаграммы состояния арматуры при растяжении и сжатии принимают одинаковыми.
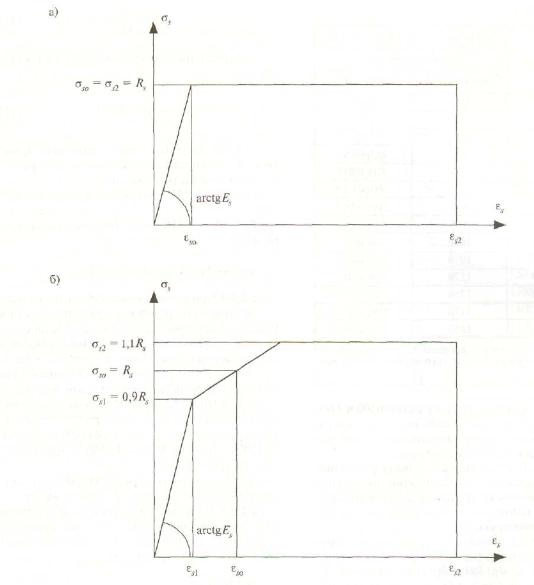
а – двухлинейная; б – трехлинейная
Рисунок 2 – Диаграммы состояния растянутой арматуры
2.2.2.8 Напряжения в арматуре σs согласно двухлинейной диаграмме состояния арматуры определяют в зависимости от относительных деформаций εs по формулам:
при 0 < ε s < ε s 0
σs = εs Es ; (13)
при ε s 0 ≤ ε s ≤ ε s 2
σs = Rs (14)
Значения ε s 0 , Es и Rs принимают согласно пп. 2.2.2.5, 2.2.2.6 и 2.2.2.2. Значения относительной деформации ε s 2 принимают равными 0,025.
2.2.2.9 Напряжения в арматуре σs согласно трехлинейной диаграмме состояния арматуры определяют в зависимости от относительных деформаций εs по формулам:
при 0 < ε s < ε s 1
σs = εs Es ; (15)
при ε s 1 ≤ ε s ≤ ε s 2
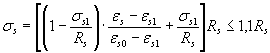 . (16)
. (16)
Значения ε s 0 , Es и Rs принимают согласно пп. 2.2.2.5, 2.2.2.6 и 2.2.2.2.
Значения напряжений σs 1 принимают равными 0,9 Rs , а напряжений σs 2 - равными 1,1 Rs .
Значения
относительных деформаций ε s 1 принимают равными ![]() , а деформации ε s 2 - равными 0,015.
, а деформации ε s 2 - равными 0,015.
2.2.3 Предварительные напряжения арматуры
2.2.3.1 Предварительные напряжения арма туры σsp принимают не более 0,9 Rs , n для горячекатаной и термомеханически упрочненной арматуры и не более 0,8 Rs , n для холоднодеформированной арматуры и арматурных канатов.
2.2.3.2 При расчете предварительно напряженных конструкций следует учитывать снижение предварительных напряжений вследствие потерь предварительного напряжения до передачи усилий натяжения на бетон (первые потери) и после передачи усилия натяжения на бетон (вторые потери).
Первые потери предварительного напряжения включают потери от релаксации предварительных напряжений в арматуре, потери от температурного перепада при термической обработке конструкций, потери от деформации анкеров и деформации формы (упоров).
Вторые потери предварительного напряжения включают потери от усадки и ползучести бетона.
2.2.3.3 Потери от релаксации напряжений арматуры Δσ sp 1 , определяют по формулам:
для арматуры классов А600 - А1000 при способе натяжения:
механическом - Δσ sp 1 = 0, l σ sp - 2,0; (17)
электротермическом - Δσ sp 1 = 0,03σ sp ; (18)
для арматуры классов Вр1200 - Вр1500, К1400, К1500 при способе натяжения:
механическом - 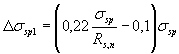 ; (19)
; (19)
электротермическом - Δσ sp 1 = 0,5σ sp . (20)
Здесь σ sp принимается без потерь в МПа.
При отрицательных значениях Δσ sp 1 принимают Δσ sp 1 = 0.
При наличии более точных данных о релаксации арматуры допускается принимать иные значения потерь от релаксации.
2.2.3.4 Потери Δσ sp 2 (МПа) от температурного перепада Δ t (° C ), определяемого как разность температур натянутой арматуры в зоне нагрева и устройства, воспринимающего усилия натяжения при нагреве бетона, принимают равными:
Δσ sp 2 = 1,25 Δ t . (21)
При отсутствии точных данных по температурному перепаду допускается принимать Δ t = 65 °С.
При наличии более точных данных о температурной обработке конструкции допускается принимать иные значения потерь от температурного перепада.
2.2.3.5 Потери от деформации стальной формы (упоров) Δσ sp 3 при неодновременном натяжении арматуры на форму определяют по формуле
![]() , (22)
, (22)
где п - число стержней (групп стержней), натягиваемых неодновременно;
Δ l - сближение упоров по линии действия усилия натяжения арматуры, определяемое из расчета деформации формы;
l - расстояние между наружными гранями упоров.
При отсутствии данных о конструкции формы и технологии изготовления допускается принимать Δσ sp 3 = 30 МПа.
При электротермическом способе натяжения арматуры потери от деформации формы не учитываются.
2.2.3.6 Потери от деформации анкеров натяжных устройств Δσ sp 4 определяют по формуле
![]() , (23)
, (23)
где Δ l - обжатие анкеров или смещение стержня в зажимах анкеров;
l - расстояние между наружными гранями упоров.
При отсутствии данных допускается принимать Δ l = 2 мм.
При электротермическом способе натяжения арматуры потери от деформации анкеров не учитывают.
2.2.3.7 Потери от усадки бетона Δσ sp 5 определяют по формуле
Δσ sp5 = εb,sh Es, (24)
где εb , sh - деформации усадки бетона, значения которых можно приближенно принимать в зависимости от класса бетона равными:
0,0002 - для бетона классов В35 и ниже;
0,00025 - для бетона класса В40;
0,0003 - для бетона классов В45 и выше.
Допускается потери от усадки бетона определять более точными методами.
2.2.3.8 Потери от ползучести бетона Δσ sp 6 определяют по формуле
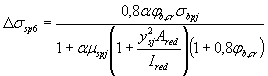 , (25)
, (25)
где φ b , cr - коэффициент ползучести бетона, определяемый согласно п. 2.1.2.7;
σbpj - напряжения в бетоне на уровне центра тяжести рассматриваемой j -й группы стержней напрягаемой арматуры;
ysj - расстояние между центрами тяжести сечения рассматриваемой группы стержней напрягаемой арматуры и приведенного поперечного сечения элемента;
Ared , Ired - площадь приведенного сечения элемента и ее момент инерции относительно центра тяжести приведенного сечения;
μ spj - коэффициент армирования, равный Aspj / А, где А и Aspj - площади поперечного сечения соответственно элемента и рассматриваемой группы стержней напрягаемой арматуры.
Допускается потери от ползучести бетона определять более точными методами.
Напряжения
σbpj определяют по
правилам расчета упругих материалов, принимая приведенное сечение элемента,
включающее площадь сечения бетона и площадь сечения всей продольной арматуры
(напрягаемой и ненапрягаемой) с коэффициентом приведения арматуры к бетону ![]() согласно п. 2.2.3.10.
согласно п. 2.2.3.10.
2.2.3.9 Полные значения первых потерь предварительного напряжения арматуры (по пп. 2.2.3.3- 2.2.3.6) определяют по формуле
![]() , (26)
, (26)
где i - номер потерь предварительного напряжения.
Усилие предварительного обжатия бетона с учетом первых потерь равно:
![]() , (27)
, (27)
где Aspj и σsp (1) j - площадь сечения j - й группы стержней напрягаемой арматуры в сечении элемента и предварительное напряжение в группе с учетом первых потерь
σsp (1) j = σspj - Δ σsp (1) j .
Здесь σspj - начальное предварительное напряжение рассматриваемой группы стержней арматуры.
Полные значения первых и вторых потерь предварительного напряжения арматуры (по пп. 2.2.3.3- 2.2.3.8) определяют по формуле
![]() . (28)
. (28)
Усилие в напрягаемой арматуре с учетом полных потерь равно:
![]() , (29)
, (29)
где σsp (2) j = σspj - Δ σsp (2) j .
При проектировании конструкций полные суммарные потери Δ σsp (2) j для арматуры, расположенной в растянутой при эксплуатации зоне сечения элемента, следует принимать не менее 100 МПа.
При определении усилия предварительного обжатия бетона Р с учетом полных потерь напряжений следует учитывать сжимающие напряжения в ненапрягаемой арматуре, численно равные сумме потерь от усадки и ползучести бетона на уровне этой арматуры.
2.2.3.10 Предварительные напряжения в бетоне σ bp при передаче усилия предварительного обжатия Р(1), определяемого с учетом первых потерь, не должны превышать: если напряжения уменьшаются или не изменяются при действии внешних нагрузок - 0,9 Rbp ; если напряжения увеличиваются при действии внешних нагрузок - 0,7 Rbp .
Напряжения в бетоне σ bp определяют по формуле
![]() , (30)
, (30)
где Р(1) - усилие предварительного обжатия с учетом первых потерь;
М - изгибающий момент от внешней нагрузки, действующей в стадии обжатия (собственный вес элемента);
e 0 p - эксцентриситет усилия Р(1) относительно центра тяжести приведенного поперечного сечения элемента;
у - расстояние от центра тяжести приведенного сечения до рассматриваемого волокна.
2.2.3.11 Длину зоны передачи предварительного напряжения на бетон для арматуры без дополнительных анкерующих устройств определяют по формуле
![]() , (31)
, (31)
но не менее 10 ds и 200 мм, а для арматурных канатов - также не менее 300 мм.
В формуле (31):
σ sp - предварительное напряжение в напрягаемой арматуре с учетом первых потерь;
Rbond - сопротивление сцепления напрягаемой арматуры с бетоном, отвечающее передаточной прочности бетона и определяемое согласно п. 5.3;
As , us - площадь и периметр стержня арматуры.
Передачу предварительного напряжения с арматуры на бетон рекомендуется осуществлять плавно.
3 р асчет элементов предварительно напряженных железобетонных конструкций по предельным состояниям первой группы
3.1 Расчет предварительно напряженных железобетонных элементов по прочности
3.1.1 Общие положения
3.1.1.1 В настоящем СП приведены указания по расчету изгибаемых предварительно напряженных элементов.
Расчет предварительно напряженных элементов производят для стадии эксплуатации на действие изгибающих моментов и поперечных сил от внешних нагрузок и для стадии предварительного обжатия на действие усилий от предварительного натяжения арматуры и усилий от внешних нагрузок, действующих в стадии обжатия.
3.1.1.2 Расчет по прочности пред напряженных элементов при действии изгибающих моментов следует производить для сечений, нормальных к их продольной оси.
Расчет по прочности в общем случае производят на основе нелинейной деформационной модели согласно п. 3.1.4.
Допускается расчет железобетонных элементов прямоугольного, таврового и двутаврового сечений с арматурой, расположенной у перпендикулярной плоскости изгиба граней элемента, при действии усилий в плоскости симметрии нормальных сечений производить на основе предельных усилий согласно пп. 3.1.2 и 3.1.3.
3.1.1.3 Для железобетонных элементов, у которых предельное усилие по прочности оказывается меньше предельного усилия по образованию трещин ( п. 4.2.2), площадь сечения продольной растянутой арматуры должна быть увеличена по сравнению с требуемой из расчета по прочности не менее чем на 15% или должна удовлетворять расчету по прочности на действие момента образования трещин.
3.1.1.4 Расчет преднапряженных элементов в стадии обжатия производят как при внецентренном сжатии усилием предварительного обжатия в предельном состоянии согласно п. 3.1.3.1.
3.1.1.5 Расчет по прочности предварительно напряженных элементов при действии поперечных сил следует производить для сечений, наклонных к их продольной оси ( п. 3.1.5).
3.1.1.6 При расчете предварительно напряженных элементов по прочности следует учитывать возможные отклонения предварительного напряжения, определяемого согласно п. 2.2.3.9 путем умножения значений σ spj (или усилия обжатия Р j ) для рассматриваемого j - г o стержня или группы стержней напрягаемой арматуры на коэффициент γ sp .
Значения коэффициента γ sp принимают равными:
0,9 - при благоприятном влиянии предварительного напряжения;
1,1 - при неблагоприятном влиянии предварительного напряжения.
3.1.2 Расчет предварительно напряженных элементов на действие изгибающих моментов в стадии эксплуатации но предельным усилиям
3.1.2.1 Предельные усилия в сечении, нормальном к продольной оси элемента, следует определять исходя из следующих предпосылок:
сопротивление бетона растяжению принимают равным нулю;
сопротивление бетона сжатию представляется напряжениями, равными Rb и равномерно распределенными по сжатой зоне бетона;
растягивающие напряжения в арматуре принимают не более расчетного сопротивления растяжению Rs ;
сжимающие напряжения в арматуре принимают не более расчетного сопротивления сжа тию Rsc .
Допускается принимать для растянутой арматуры с условным пределом текучести напряжения выше Rs , но не более 1,1 Rs в зависимости от соотношения ζ и ζ R (п. 3.1.2.2).
3.1.2.2 Расчет по прочности нормальных сечений следует производить
в зависимости от соотношения между значением относительной высоты сжатой зоны
бетона ![]() , определяемой из соответствующих условий равновесия, и
значением граничной относительной высоты сжатой зоны ζ R , при которой предельное состояние
элемента наступает одновременно с достижением в растянутой арматуре напряжения,
равного расчетному сопротивлению Rs .
, определяемой из соответствующих условий равновесия, и
значением граничной относительной высоты сжатой зоны ζ R , при которой предельное состояние
элемента наступает одновременно с достижением в растянутой арматуре напряжения,
равного расчетному сопротивлению Rs .
3.1.2.3 Значение ζ R определяют по формуле
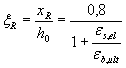 , (32)
, (32)
где ε s , el - относительная деформация арматуры растянутой зоны, вызванная внешней нагрузкой при достижении в этой арматуре напряжения, равного Rs ;
ε b , ult - относительная деформация сжатого бетона при напряжениях, равных Rb , принимаемая равной 0,0035.
Для арматуры с условным пределом текучести значение ε s , el определяют по формуле
![]() , (33)
, (33)
где σ sp - предварительное напряжение в арматуре с учетом всех потерь и γ sp = 0,9; 400 - в МПа.
Для
ненапрягаемой арматуры с физическим пределом текучести ![]() .
.
3.1.2.4 Для напрягаемой арматуры, расположенной в сжатой зоне, расчетное сопротивление сжатию Rsc ( пп. 3.1.2.6, 3.1.2.7) должно быть заменено напряжением σ sc , равным (МПа):
(500 - σ΄ sp ) - при учете коэффициента условий работы бетона γb 1 = 0,9 ( п. 2.1.2.3);
(400 - σ΄ sp ) - при γb 1 = 1,0.
Значения σ΄ sp определяют с коэффициентом γsp = 1,1.
Во всех случаях напряжение σ sc принимают не более Rsc .
3.1.2.5 Расчет по прочности сечений изгибаемых элементов производят из условия
М ≤ Ми lt (34)
где М - изгибающий момент от внешней нагрузки;
Mult - предельный изгибающий момент, который может быть воспринят сечением элемента.
3.1.2.6 Значение Mult для изгибаемых элементов прямоугольного
сечения (рисунок 3) при ![]() определяют по
формуле
определяют по
формуле
Mult = Rb b x (h0- 0,5 х ) + Rsc A's (h0 - а '); (35)
при этом высоту сжатой зоны х определяют по формуле
![]() . (36)
. (36)
В формулах этого пункта и п. 3.1.2.7 обозначения площадей сечения As и A ' s относятся как к напрягаемой, так и к ненапрягаемой арматуре.
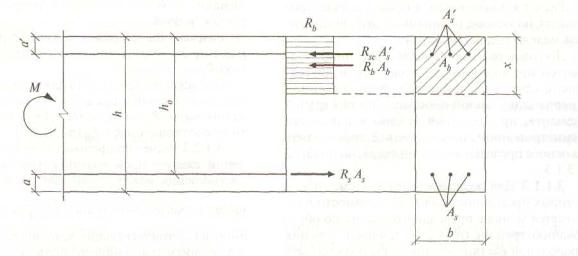
Рисунок 3 - Схема усилий и эпюра напряжений в сечении, нормальном к продольной оси изгибаемого предварительно напряженного элемента при его расчете по прочности
3.1.2.7 Значение
Mult для изгибаемых элементов,
имеющих полку в сжатой зоне (тавровые и двутавровые сечения), при ![]() определяют в
зависимости от положения границы сжатой зоны:
определяют в
зависимости от положения границы сжатой зоны:
а) если граница проходит в полке (рисунок 4,а), т.е. соблюдается условие
Rs As ≤ Rb b 'f h'f + Rsc A's , (37)
значение Mult определяют по п. 3.1.2.6 как для прямоугольного сечения шириной b ' f ;
б) если граница проходит в ребре (рисунок 4,б), т.е. условие (37) не соблюдается, значение Mult определяют по формуле
Mult = Rb b x ( h 0 - 0,5х) + Rb ( b ' f - b )× h ' f ( h 0 - 0,5 h ' f ) + Rsc A ' s ( h 0 - a '); (38)
при этом высоту сжатой зоны бетона х определяют по формуле
![]() . (39)
. (39)
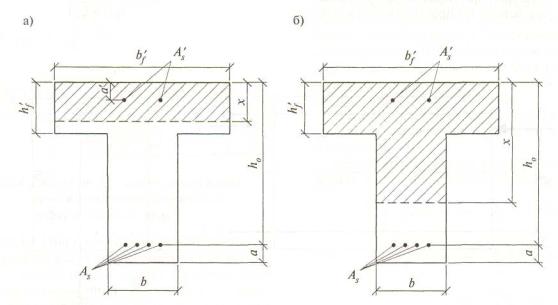
а – в полке; б – в ребре
Рисунок 4 - Положение границы сжатой зоны в сечении изгибаемого предварительно
3.1.2.8 Значение b ' f , вводимое в расчет, принимают из условия, что ширина свеса полки в каждую сторону от ребра должна быть не более 1/6 пролета элемента и не более:
а) при наличии поперечных ребер или при h ' f ≥ 0,1 h - 1/2 расстояния в свету между продольными ребрами;
б) при отсутствии поперечных ребер (или при расстояниях между ними больших, чем расстояния между продольными ребрами) и h ' f < 0,1 h - 6 h ' f ;
в) при консольных свесах полки:
при h ' f ≥ 0,1 h ..................... 6 h ' f ;
при 0,05 h ≤ h ' f < 0,1 h ........ 3 h ' f ;
при h ' f < 0,05 h - свесы не учитывают.
3.1.2.9 При расчете по прочности изгибаемых элементов рекомендуется соблюдать условие x ≤ ξ R h 0 .
В случае когда по конструктивным соображениям или из расчета по предельным состояниям второй группы площадь растянутой арматуры принята большей, чем это требуется для соблюдения условия х ≤ ξR h 0 , допускается предельный изгибающий момент Mult определять по формуле (35) или (38), подставляя в нее значения высоты сжатой зоны х = ξR h 0 .
3.1.3 Расчет предварительно напряженных элементов в стадии предварительного обжатия
3.1.3.1 При расчете элемента в стадии предварительного обжатия усилие в напрягаемой арматуре вводится в расчет как внешняя продольная сила, равная:
Np = (σ'sp - 330) A'sp + σsp Asp, (40)
где A ' sp и Asp - площадь сечения напрягаемой арматуры, расположенной соответственно в наиболее обжатой и в растянутой (менее обжатой) зонах сечения;
σ ' sp и σsp - предварительные напряжения с учетом первых потерь и коэффициента γ sp = 1,1 в арматуре с площадью сечения A ' sp и А sp .
3.1.3.2 Расчет по прочности элементов прямоугольного сечения в стадии предварительного обжатия производят из условия
Np ep < Rb b x (h0 - 0,5x) + Rsc A's (h0 - a'), (41)
где е p - расстояние от точки приложения продольной силы N p с учетом влияния изгибающего момента М от внешней нагрузки, действующей в стадии изготовления (собственный вес элемента), до центра тяжести сечения ненапрягаемой арматуры, растянутой или наименее сжатой (при полностью сжатом сечении элемента) от этих усилий ( рисунок 5), определяемое по формуле
![]() , (42)
, (42)
е0 p - расстояние от точки приложения силы Np до центра тяжести сечения элемента;
Rb - расчетное сопротивление бетона сжатию, принимаемое как для класса бетона по прочности на сжатие, численно равного передаточной прочности бетона Rbp , по линейной интерполяции ( таблица 2);
Rsc - расчетное сопротивление ненапрягаемой арматуры сжатию, принимаемое в стадии предварительного обжатия не более 330 МПа;
A ' s - площадь сечения ненапрягаемой арматуры, расположенной в наиболее сжатой зоне сечения элемента.
Высоту
сжатой зоны бетона х определяют в зависимости от величины ξ R , определяемой по формуле (32) с подстановкой в нее значения ![]() , где Rs - расчетное
сопротивление растянутой ненапрягаемой арматуры As , и ε b , ult = 0,003:
, где Rs - расчетное
сопротивление растянутой ненапрягаемой арматуры As , и ε b , ult = 0,003:
а) при ![]() (см. рисунок 5) по фор муле
(см. рисунок 5) по фор муле
![]() ; (43)
; (43)
б) при ![]() (где х - см.
поз. а) по формуле
(где х - см.
поз. а) по формуле
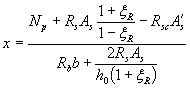 . (44)
. (44)
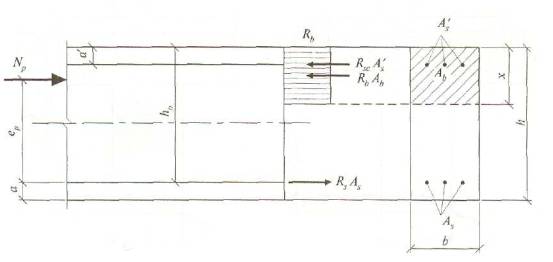
Рисунок 5 - Схема усилий и эпюра напряжений в сечении, нормальном к продольной оси изгибаемого предварительно напряженного элемента при его расчете по прочности в стадии обжатия
3.1.3.3 Расчет по прочности элементов таврового и двутаврового сечений в стадии предварительного обжатия производят в зависимости от положения границы сжатой зоны:
а) если граница сжатой зоны проходит в полке (см. рисунок 4,а), т.е. соблюдается условие
Np ≤ Rb b 'f h'f – Rs As + Rsc A's , (45)
расчет производят как для прямоугольного сечения шириной b ' f согласно п. 3.1.3.2;
б) если граница сжатой зоны проходит в ребре (см. рисунок 4,б), т.е. условие (45) не соблюдается, расчет производят из условия
Np ep ≤ Rb b x ( h 0 - 0,5х) + Rb ( b ' f - b )× h ' f ( h 0 - 0,5 h ' f ) + Rsc A ' s ( h 0 - a '); (46)
где
![]() ; e 0 p - см. п. 3.1.3.2;
; e 0 p - см. п. 3.1.3.2;
zs - расстояние от центра тяжести сечения элемента до растянутой (наименее сжатой) ненапрягаемой арматуры.
Высоту сжатой зоны определяют по формулам:
а) при ![]() (ξ R - см. п. 3.1.3.2 )
(ξ R - см. п. 3.1.3.2 )
![]() ; (47)
; (47)
б) при ![]()
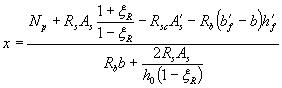 . (48)
. (48)
3.1.4 Расчет по прочности нормальных сечений на основе нелинейной деформационной модели
3.1.4.1 При расчете по прочности усилия и деформации в сечении, нормальном к продольной оси элемента, определяют на основе нелинейной деформационной модели, использующей уравнения равновесия внешних сил и внутренних усилий в сечении элемента, а также следующие положения:
распределение относительных деформаций бетона и арматуры по высоте сечения элемента от внешней нагрузки принимают по линейному закону (гипотеза плоских сечений);
связь между осевыми напряжениями и относительными деформациями бетона и арматуры принимают в виде диаграмм состояния (деформирования) бетона и арматуры ( пп. 2.1.2.10, 2.2.2.7);
сопротивление бетона растянутой зоны допускается не учитывать, принимая при ε bi ≥ 0 напряжения σ bi = 0.
3.1.4.2 Переход от эпюры напряжений в бетоне к обобщенным внутренним усилиям определяют с помощью процедуры численного интегрирования напряжений по нормальному сечению. Для этого нормальное сечение условно разделяют на малые участки: при косом изгибе - по высоте и ширине сечения; при изгибе в плоскости оси симметрии поперечного сечения элемента - только по высоте сечения. Напряжения в пределах малых участков принимают равномерно распределенными (усредненными).
3.1.4.3 При расчете элементов с использованием нелинейной деформационной модели принимают:
значения сжимающей продольной силы, а также сжимающих напряжений и деформаций укорочения бетона и арматуры со знаком « - »;
значения растягивающей продольной силы, а также растягивающих напряжений и деформаций удлинения бетона и арматуры со знаком « + ».
Знаки координат центров тяжести арматурных стержней и выделенных участков бетона, а также точки приложения продольной силы принимают в соответствии с назначенной системой координат Х0 Y . В общем случае начало координат этой системы (точка 0 на рисунке 6) располагают в произвольном месте в пределах поперечного сечения элемента.
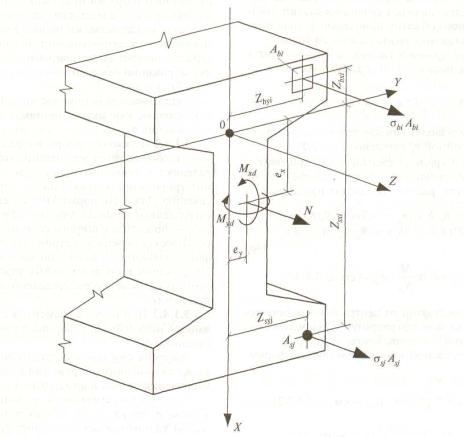
Рисунок 6 – Расчетная схема нормального сечения железобетонного элемента
3.1.4.4 При расчете нормальных сечений по прочности (см. рисунок 6) в общем случае используют:
уравнения равновесия внешних сил и внутренних усилий в нормальном сечении элемента
![]() ; (49)
; (49)
![]() ; (50)
; (50)
![]() ; (51)
; (51)
уравнения, определяющие распределение деформаций от действия внешней нагрузки по сечению элемента
![]() ; (52)
; (52)
![]() ; (53)
; (53)
зависимости, связывающие напряжения и относительные деформации бетона и арматуры:
бетона
σ bi = Eb νbi εbi ; (54)
ненапрягаемой арматуры
σ sj = Esj νsj εsj ; (55)
напрягаемой арматуры
σ sj = Esj νsj ( εsj + ε spj ). (56)
В уравнениях (49)-(56):
Мх, Му - изгибающие моменты от внешней нагрузки относительно выбранных и располагаемых в пределах поперечного сечения элемента координатных осей (соответственно действующих в плоскостях X 0 Z и У0Z или параллельно им), определяемые по формулам:
Mx = Mxd + N ex; (57)
My = Myd + N ey, (58)
|
где |
Mxd , Myd |
- изгибающие моменты в соответствующих плоскостях от внешней нагрузки, определяемые из статического расчета конструкции; |
|
|
N |
- продольная сила от внешней нагрузки; для изгибаемых предварительно напряженных элементов N = 0; |
|
|
ех, ey |
- расстояния от точки приложения силы N до соответствующих выбранных осей; |
|
|
А bi , Zbxi , Zbyi , σbi |
- площадь, координаты центра тяжести i -го участка бетона и напряжение на уровне его центра тяжести; |
|
|
||
|
|
Asj , Zsxj , Zsyj , σsj |
- площадь, координаты центра тяжести j - го стержня арматуры и напряжение в нем; |
|
|
||
|
|
ε 0 |
- относительная деформация волокна, расположенного на пересечении выбранных осей (в точке 0); |
|
|
εbi |
- относительная деформация бетона от действия внешней нагрузки; |
|
|
εsj |
- относительная деформация арматуры от действия внешней нагрузки; |
|
|
εspj |
- относительная деформация предварительного напряжения арматуры с учетом относительных деформаций потерь предварительного напряжения, отвечающих рассматриваемой расчетной стадии; |
|
|
|
- кривизна продольной оси в рассматриваемом поперечном сечении элемента в плоскостях действия изгибающих моментов М x и My ; |
|
|
Eb |
- начальный модуль упругости бетона; |
|
|
Esj |
- модуль упругости j - го стержня арматуры; |
|
|
ν bi |
- коэффициент упругости бетона i-го участка; |
|
|
ν sj |
- коэффициент упругости j -го стержня арматуры |
Коэффициенты vbi и ν sj принимают по соответствующим диаграммам состояния бетона и арматуры, указанным в пп. 2.1.2.10, 2.2.2.7.
Значения коэффициентов vbl и ν sj определяют как соотношение значений напряжений и деформаций для рассматриваемых точек соответствующих диаграмм состояния бетона и арматуры, принятых в расчете, деленное на модуль упругости бетона Е b (при двухлинейной диаграмме состояния бетона - на приведенный модуль деформации Е b , red ) и арматуры Es . При этом используют зависимости «напряжение - деформация» (4) - (8), (13) и (16) на рассматриваемых участках диаграмм.
![]() ; (58)
; (58)
![]() . (59)
. (59)
3.1.4.5 Расчет нормальных сечений железобетонных элементов по прочности производят из условий
![]() ; (60)
; (60)
![]() , (61)
, (61)
где εb , max - относительная деформация наиболее сжатого волокна бетона в нормальном сечении;
εs , max - относительная деформация наиболее растянутого стержня арматуры в нормальном сечении;
ε b , ult - предельное значение относительной деформации бетона при сжатии, принимаемое согласно указаниям п. 3.1.4.6;
ε s , ult - предельное значение относительной деформации удлинения арматуры, принимаемое согласно указаниям п. 3.1.4.6.
3.1.4.6 Предельные значения относительных деформаций бетона ε b , ult (ε bt , ult ) принимают при двузначной эпюре деформаций (сжатие и растяжение) в поперечном сечении бетона элемента (изгиб, внецентренное сжатие или растяжение с большими эксцентриситетами), равными ε b 2 (ε bt 2 ).
При внецентренном сжатии или растяжении элементов и распределении в поперечном сечении бетона элемента деформаций только одного знака предельные значения относительных деформаций бетона ε b , ult (ε bt , ult ) определяют в зависимости от соотношения деформаций бетона на противоположных гранях сечения элемента ε1 и ε2 (|ε2| ≥ |ε1|) по формулам:
![]() ; (62)
; (62)
![]() , (63)
, (63)
где ε b 0 , ε bt 0 , ε b 2 , ε bt 2 - деформационные параметры расчетных диаграмм состояния бетона (п п. 2.1.2.5, 2.1.2.11, 2.1.2.13, 2.1.2.14).
Предельное значение относительной деформации арматуры εs , ult принимают равным:
0,025 - для арматуры с физическим пределом текучести;
0,015 - для арматуры с условным пределом текучести.
3.1.5 Расчет предварительно напряженных элементов при действии поперечных сил
Общие положения
3.1.5.1 Расчет по прочности железобетонных элементов при действии поперечных сил производят на основе модели наклонных сечений.
При расчете по модели наклонных сечений должны быть обеспечены прочность элемента по полосе между наклонными сечениями и наклонному сечению на действие поперечных сил, а также прочность по наклонному сечению на действие момента.
Прочность по наклонной полосе характеризуется максимальным значением поперечной силы, которое может быть воспринято наклонной полосой, находящейся под воздействием сжимающих усилий вдоль полосы и растягивающих усилий от поперечной арматуры, пересекающей наклонную полосу. При этом прочность бетона определяют по сопротивлению бетона осевому сжатию с учетом влияния сложного напряженного состояния в наклонной полосе.
Расчет по наклонному сечению на действие поперечных сил производят на основе уравнения равновесия внешних и внутренних поперечных сил, действующих в наклонном сечении с длиной проекции с на продольную ось элемента. Внутренние поперечные силы включают поперечную силу, воспринимаемую бетоном в наклонном сечении, и поперечную силу, воспринимаемую пересекающей наклонное сечение поперечной арматурой. При этом поперечные силы, воспринимаемые бетоном и поперечной арматурой, определяют по сопротивлениям бетона и поперечной арматуры растяжению с учетом длины проекции с наклонного сечения.
Расчет по наклонному сечению на действие момента производят на основе уравнения равновесия моментов от внешних и внутренних сил, действующих в наклонном сечении с длиной проекции с на продольную ось элемента. Моменты от внутренних сил включают момент, воспринимаемый пересекающей наклонное сечение продольной растянутой арматурой, и момент, воспринимаемый пересекающей наклонное сечение поперечной арматурой. При этом моменты, воспринимаемые продольной и поперечной арматурой, определяют по сопротивлениям продольной и поперечной арматуры растяжению с учетом длины проекции с наклонного сечения.
Расчет железобетонных элементов по полосе между наклонными сечениями
3.1.5.2 Расчет предварительно напряженных элементов по бетонной полосе между наклонными сечениями производят из условия
Q ≤ φ b1 Rb b h0, (64)
где Q - поперечная сила в нормальном сечении элемента;
φ b 1 - коэффициент, принимаемый равным 0,3.
Расчет железобетонных элементов по наклонным сечениям на действие поперечных сил
3.1.5.3 Расчет предварительно напряженных изгибаемых элементов по наклонному сечению ( рисунок 7) производят из условия
Q ≤ Qb + Qsw (65)
где Q - поперечная сила в наклонном сечении с длиной проекции с на продольную ось элемента, определяемая от всех внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения; при этом учитывают наиболее опасное загружение в пределах наклонного сечения;
Qb - поперечная сила, воспринимаемая бетоном в наклонном сечении;
Qsw - поперечная сила, воспринимаемая поперечной арматурой в наклонном сечении.
Поперечную силу Qb определяют по формуле
![]()
![]() , (66)
, (66)
но принимают не более 2,5 Rbtbh 0 и не менее 0,5 Rbtbh 0 ;
φ b 2 - коэффициент, принимаемый равным 1,5.
Допускается значение Qb определять с учетом влияния усилия предварительного обжатия Р напрягаемой арматурой.
Усилие Qsw для поперечной арматуры, нормальной к продольной оси элемента, определяют по формуле
Qsw = φ sw qsw c , (67)
где φ sw - коэффициент, принимаемый равным 0,75;
qsw - усилие в поперечной арматуре на единицу длины элемента
![]() . (68)
. (68)
Расчет производят для ряда расположенных по длине элемента наклонных сечений при наиболее опасной длине проекции наклонного сечения с. При этом длину с в формуле (67) принимают не более 2,0 h 0 .
Допускается производить расчет наклонных сечений, не рассматривая наклонные сечения при определении поперечной силы от внешней нагрузки, из условия
Q1 ≤ Qb1 + Qsw,1 (69)
где Q 1 - поперечная сила в нормальном сечении от внешней нагрузки;
Qb1 = 0,5Rbt b h0; (70)
Qsw,1 = qsw h0. (71)
При
расположении нормального сечения, в котором учитывают поперечную силу Q 1 вблизи опоры на
расстоянии а менее 2,5 h 0 расчет из
условия (69) производят, умножая значения Qbl , определяемые по формуле (70), на коэффициент, равный ![]() , но принимают значение Qbl не более 2,5 Rbl b h 0 .
, но принимают значение Qbl не более 2,5 Rbl b h 0 .
При расположении нормального сечения, в котором учитывают поперечную силу Q 1 на расстоянии а менее h 0 расчет из условия (69) производят, умножая значение Qsw ,1 , определяемое по формуле (71), на коэффициент, равный a / h 0 .
Поперечную арматуру учитывают в расчете, если соблюдается условие
qsw ≥ 0,25Rbt b.
Можно учитывать поперечную арматуру и при невыполнении этого условия, если в условии (65) принимать
Qb = 4φb2 h02 qsw/c .
Шаг
поперечной арматуры, учитываемой в расчете, ![]() должен быть не больше
значения
должен быть не больше
значения ![]() .
.
При отсутствии поперечной арматуры или нарушении указанных выше требований расчет производят из условия (65) или (69), принимая усилие Qsw или Qsw ,1 равным нулю.
Поперечная арматура должна отвечать конструктивным требованиям, приведенным в СП 52-101 .
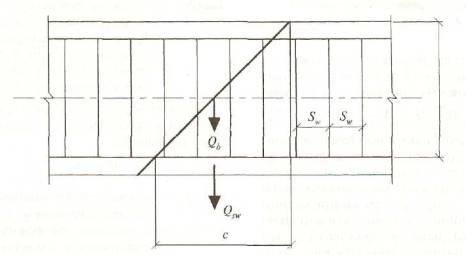
Рисунок 7 - Схема усилий при расчете изгибаемых предварительно напряженных элементов по наклонному сечению на действие поперечных сил
Расчет железобетонных элементов по наклонным сечениям на действие моментов
3.1.5.4 Расчет предварительно напряженных элементов по наклонным сечениям на действие моментов (рисунок 8) производят из условия
М < Ms + Msw, (72)
где М - момент в наклонном сечении с длиной проекции с на продольную ось элемента, определяемый от всех внешних сил, расположенных по одну сторону от рассматриваемого наклонного сечения, относительно конца наклонного сечения (точка 0), противоположного концу, у которого располагается проверяемая продольная арматура, испытывающая растяжение от момента в наклонном сечении; при этом учитывают наиболее опасное загружение в пределах наклонного сечения;
Ms - момент, воспринимаемый продольной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения (точка 0);
Msw - момент, воспринимаемый поперечной арматурой, пересекающей наклонное сечение, относительно противоположного конца наклонного сечения (точка 0).
Момент Ms определяют по формуле
Ms = Ns zs, (73)
где Ns - усилие в продольной растянутой арматуре, принимаемое равным Rs As , а в зоне анкеровки - определяемое согласно п. 5.3.4;
zs - плечо внутренней пары сил; допускается принимать zs = 0,9 h 0 .
Момент Msw для поперечной арматуры, нормальной к продольной оси элемента, определяют по формуле
Msw = 0,5 Qsw c, (74)
где Qsw - усилие в поперечной арматуре, принимаемое равным qsw c ;
qsw - определяют по формуле (68), а с принимают в пределах от 1,0 h 0 до 2,0 h 0 ,
Расчет производят для наклонных сечений, расположенных по длине элемента на его концевых участках и в местах обрыва продольной арматуры, при наиболее опасной длине проекции наклонного сечения с, принимаемой в указанных выше пределах.
Допускается производить расчет наклонных сечений, принимая в условии (72) момент М в наклонном сечении при длине проекции с на продольную ось элемента, равной 2,0 h 0 , а мо мент Msw - равным 0,5 qsw h 0 2 .
При отсутствии поперечной арматуры расчет наклонных сечений производят из условия (72), принимая момент М в наклонном сечении при длине проекции с на продольную ось элемента, равной 2,0 h 0 , а момент М sw - равным нулю.
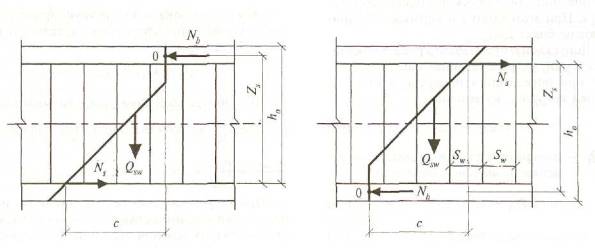
Рисунок 8 - Схема усилий при расчете изгибаемых предварительно напряженных элементов по наклонному сечению на действие моментов
4 р асчет предварительно напряженных элементов железобетонных конструкций по предельным состояниям второй группы
4.1 Общие положения
4.1.1 Расчеты по предельным состояниям второй группы включают:
- расчет по раскрытию трещин;
- расчет по деформациям.
4.1.2 Расчет по образованию трещин производят для проверки необходимости расчета по раскрытию трещин, а также для проверки необходимости учета трещин при расчете по деформациям.
Требования по отсутствию трещин предъявляют к предварительно напряженным конструкциям, у которых при полностью растянутом сечении должна быть обеспечена непроницаемость (находящихся под давлением жидкости или газов, испытывающих воздействие радиации и т.п.), к уникальным конструкциям, а также к конструкциям при воздействии сильно агрессивной среды.
4.1.3 При расчете по предельным состояниям второй группы нагрузки принимают с коэффициентом надежности по нагрузке γ f = 1,0.
4.1.4 Расчет изгибаемых предварительно напряженных элементов по предельным состояниям второй группы производят как при внецентренном сжатии на совместное действие усилий от внешней нагрузки М и продольной силы N p равной усилию предварительного обжатия Р.
4.2 Расчет предварительно напряженных железобетонных элементов по раскрытию трещин
4.2.1 Общие положения
4.2.1.1 Расчет предварительно напряженных изгибаемых элементов по раскрытию трещин производят в тех случаях, когда соблюдается условие
М > М crc , (75)
где М - изгибающий момент от внешней нагрузки;
М crc - изгибающий момент, воспринимаемый нормальным сечением элемента при образовании трещин, определяемый согласно п. 4.2.2.
Для центрально растянутых элементов ширину раскрытия трещин определяют при соблюдении условия
N > Ncrc, (76)
где N - продольное растягивающее усилие от внешней нагрузки;
N crc - продольное растягивающее усилие, воспринимаемое элементом при образовании трещин.
4.2.1.2 Расчет железобетонных элементов производят по непродолжительному и продолжительному раскрытию трещин.
Непродолжительное раскрытие трещин определяют от совместного действия постоянных и временных (длительных и кратковременных) нагрузок, продолжительное - только от постоянных и временных длительных нагрузок ( п. 1.2.4).
4.2.1.3 Расчет по раскрытию трещин производят из условия
acrc ≤ acrc,ult , (77)
где acrc - ширина раскрытия трещин от действия внешней нагрузки, определяемая согласно пп. 4.2.1.4 и 4.2.3;
acrc , ult - предельно допустимая ширина раскрытия трещин.
Значения acrc , ult принимают равными:
а) из условия обеспечения сохранности арматуры:
- классов А240 - А600, В500:
0,3 мм - при продолжительном раскрытии трещин;
0,4 мм - при непродолжительном раскрытии трещин;
- классов А800, А1000, а также Вр1200 - Вр1400, К1400, К1500 (К-19) и К1500 (К-7) диаметром 12 мм:
0,2 мм - при продолжительном раскрытии трещин;
0,3 мм - при непродолжительном раскрытии трещин;
- классов Вр1500, К1500 (К-7) диаметром 6 и 9 мм:
0,1 мм - при продолжительном раскрытии трещин;
0,2 мм - при непродолжительном раскрытии трещин;
б) из условия ограничения проницаемости конструкций:
0,2 мм - при продолжительном раскрытии трещин;
0,3 мм - при непродолжительном раскрытии трещин.
4.2.1.4 ширину раскрытия трещин acrc определяют исходя из взаимных смещений растянутой арматуры и бетона по обе стороны трещины на уровне оси арматуры и принимают:
- при продолжительном раскрытии
acrc = acrc ,1 ; (78)
- при непродолжительном раскрытии
acrc = acrc ,1 + acrc ,2 - acrc ,3 , (79)
где acrc ,1 - ширина раскрытия трещин от продолжительного действия постоянных и временных длительных нагрузок;
acrc ,2 - ширина раскрытия трещин от непродолжительного действия постоянных и временных (длительных и кратковременных) нагрузок;
acrc ,3 - ширина раскрытия трещин от непродолжительного действия постоянных и временных длительных нагрузок.
4.2.2 Определение момента образования трещин, нормальных к продольной оси элемента
4.2.2.1 Изгибающий момент Мс r с при об разовании трещин можно определять соглас но п. 4.2.2.2 или по деформационной модели согласно п. 4.2.2.7.
4.2.2.2 Определение момента образования трещин производят с учетом неупругих деформаций растянутого бетона согласно п. 4.2.2.3.
Допускается момент образования трещин определять без учета неупругих деформаций растянутого бетона по п. 4.2.2.4. Если при этом условия (77) и (97) не удовлетворяются, то момент образования трещин следует определять с учетом неупругих деформаций растянутого бетона.
4.2.2.3 Момент образования трещин с учетом неупругих деформаций растянутого бетона определяют с учетом следующих положений:
- сечения после деформирования остаются плоскими;
- эпюру напряжений в сжатой зоне бетона принимают треугольной формы как для упругого тела;
- эпюру напряжений в растянутой зоне бетона принимают трапециевидной формы с напряжениями, не превышающими расчетных значений сопротивления бетона растяжению Rbt , ser ;
- относительную деформацию крайнего растянутого волокна бетона принимают равной ее предельному значению εbt , ult при кратковременном действии нагрузки ( п. 3.1.4.6); при двухзначной эпюре деформаций в сечении элемента εbt , ult = 0,00015;
- напряжения в арматуре принимают в зависимости от относительных деформаций как для упругого тела.
4.2.2.4 Момент образования трещин предварительно напряженных изгибаемых элементов без учета неупругих деформаций растянутого бетона определяют как для сплошного упругого тела по формуле
Mcrc = Rbt,ser W + P e яр , (80)
где W - момент сопротивления приведенного сечения для крайнего растянутого волокна;
e яр = е0р + r - расстояние от точки приложения усилия предварительного обжатия Р до ядровой точки, наиболее удаленной от растянутой зоны, трещинообразование которой проверяется;
е0р - то же, до центра тяжести приведенного сечения;
r - расстояние от центра тяжести приведенного сечения до ядровой точки.
В формуле (80) знак « + » принимают, когда направления вращения моментов Р еяр и внешнего изгибающего момента М противоположны; « - » - когда направления совпадают.
Значения W и r определяют согласно п. 4.2.2.5.
4.2.2.5 Момент сопротивления W и расстояние от центра тяжести приведенного поперечного сечения до ядровой точки r определяют по формулам:
![]() ; (81)
; (81)
![]() , (82)
, (82)
где Ired - момент инерции приведенно го поперечного сечения отно сительно его центра тяжести
Ired = I + Is α + I 's α ; (83)
Ared - площадь приведенного попе речного сечения элемента
Ared = A + As α + A 's α; (84)
α - коэффициент приведения арматуры к бетону
![]() ;
;
A , As , A ' s - площадь поперечного сечения соответственно бетона, растянутой и сжатой арматуры;
yt - расстояние от наиболее растянутого волокна бетона до центра тяжести приведенного поперечного сечения элемента
![]() , (85)
, (85)
здесь St , red - статический момент площади приведенного поперечного сечения элемента относительно наиболее растянутого волокна бетона.
Допускается момент сопротивления W определять без учета арматуры.
В этом случае значения Is , I ' s , As , A ' s в формулах (83) и (84) принимают равными нулю.
Для изгибаемых элементов прямоугольного сечения момент сопротивления W без учета арматуры определяют по формуле
![]() . (86)
. (86)
4.2.2.6 Усилие Ncrc при образовании трещин в центрально растянутых элементах определяют по формуле
Ncrc = Ared Rbt,ser. (87)
4.2.2.7 Определение момента образования трещин на основе нелинейной деформационной модели производят исходя из общих положений, приведенных в пп. 2.1.2.15 и 3.1.4, но с учетом работы бетона в растянутой зоне нормального сечения, определяемой диаграммой состояния растянутого бетона согласно п. 2.1.2.13. Расчетные характеристики материалов принимают для предельных состояний второй группы.
Значение Мс r с определяют из решения сисемы уравнений, представленных в п. 3.1.4, принимая относительную деформацию бетона ε bt , max у растянутой грани элемента от действия внешней нагрузки равной предельному значению относительной деформации бетона при растяжении ε bt , ult определяемому согласно указаниям п. 3.1. 4.6 .
4.2.3 Расчет ширины раскрытия трещин, нормальных к продольной оси элемента
4.2.3.1 Ширину раскрытия нормальных трещин определяют по формуле
![]() , (88)
, (88)
где σ s - напряжение в продольной растянутой арматуре в нормальном сечении с трещиной от соответствующей внешней нагрузки, определяемое согласно п. 4.2.3.2;
l s - базовое (без учета влияния вида поверхности арматуры) расстояние между смежными нормальными трещинами;
ψs - коэффициент, учитывающий неравномерное распределение относительных деформаций растянутой арматуры между трещинами; допускается принимать коэффициент ψs = 1; если при этом условие (77) не удовлетворяется, значение ψs следует определять по формуле (96);
φ1 - коэффициент, учитывающий продолжительность действия нагрузки, принимаемый равным:
1,0 - при непродолжительном действии нагрузки;
1,4 - при продолжительном действии нагрузки;
φ2 - коэффициент, учитывающий профиль продольной арматуры, принимаемый равным:
0,5 - для арматуры периодического профиля и канатной;
0,8 - для гладкой арматуры (класса А240);
φ3 - коэффициент, учитывающий характер нагружения, принимаемый равным:
1,0 - для элементов изгибаемых и внецентренно сжатых;
1,2 - для растянутых элементов.
4.2.3.2 Значения напряжений σs в растянутой арматуре изгибаемых предварительно напряженных элементов от внешней нагрузки определяют по формуле
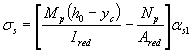 , (89)
, (89)
где Ired , Ared , yc - момент инерции, площадь приведенного поперечного сечения элемента и расстояние от наиболее сжатого волокна до центра тяжести приведенного сечения, определяемые с учетом площади сечения только сжатой зоны бетона, площадей сечения растянутой и сжатой арматуры согласно п. 4.3.3.5, принимая в соответствующих формулах значения коэффициента приведения арматуры к бетону α s 2 = α s 1 ;
N p - усилие предварительного обжатия ( п. 4.1.4);
М p - изгибающий момент от внешней нагрузки и усилия предварительного обжатия, определяемый по формуле
Mp = M ± Npe0p, (90)
где е0 p - расстояние от точки приложения усилия предварительного обжатия N p до центра тяжести приведенного сечения.
Знак « - » в формуле (90) принимают, когда направления вращений моментов М и N p е0 p не совпадают, и « + » - когда совпадают.
Значение коэффициента приведения арматуры к бетону αsl определяют по формуле
![]() , (91)
, (91)
где Eb , red - приведенный модуль деформации сжатого бетона, учитывающий неупругие деформации сжатого бетона и определяемый по формуле
![]() . (92)
. (92)
Относительную деформацию бетона ε b 1, red принимают равной 0,0015.
Допускается напряжение σs определять по формуле
![]() , (93)
, (93)
где z - расстояние от центра тяжести арматуры, расположенной в растянутой зоне сечения, до точки приложения равнодействующей усилий в сжатой зоне элемента;
е sp - расстояние от центра тяжести той же арматуры до точки приложения усилия N p .
Для элементов прямоугольного поперечного сечения при отсутствии (или без учета) сжатой арматуры значение z определяют по формуле
![]() , (94)
, (94)
где xN - высота сжатой зоны, определяемая согласно п. 4.3.3.6 с учетом влияния усилия предварительного обжатия N p .
Для элементов прямоугольного, таврового (с полкой в сжатой зоне) и двутаврового поперечного сечения допускается значение z принимать равным 0,7 h 0 .
Напряжения σs , определяемые по формулам (89) и (93), не должны превышать ( Rs , ser - σsp ).
4.2.3.3 Значения базового расстояния между трещинами ls определяют по формуле
![]() (95)
(95)
и принимают не менее 10 ds и 10 см и не более 40 ds и 40 см (для элементов с рабочей высотой поперечного сечения не более 1 м).
Здесь А bt - площадь сечения растянутого бетона;
As - площадь сечения растянутой арматуры;
ds - номинальный диаметр арматуры.
Значения А bt вычисляют согласно указаниям п. 4.2.2 из расчета по образованию трещин.
В любом случае значение А bt принимают равным площади сечения при ее высоте в пределах не менее 2а и не более 0,5 h .
4.2.3.4 Значения коэффициента ψ s определяют по формуле
![]() , (96)
, (96)
где σs , crc - напряжение в продольной растянутой арматуре в сечении с трещиной сразу после образования нормальных трещин, определяемое по указаниям п. 4.2.3.2, принимая в соответствующих формулах значения М = Мс r с ;
σs - то же, при действии рассматриваемой нагрузки.
4.3 Расчет предварительно напряженных железобетонных элементов по деформациям
4.3.1 Общие положения
4.3.1.1 Расчет предварительно напряженных элементов по деформациям производят с учетом эксплуатационных требований, предъявляемых к конструкциям.
Расчет по деформациям следует производить на действие:
постоянных, временных длительных и кратковременных нагрузок при ограничении деформаций технологическими или конструктивными требованиями;
постоянных и временных длительных нагрузок при ограничении деформаций эстетическими требованиями.
4.3.1.2 Значения предельно допустимых деформаций элементов принимают согласно СНиП 2.01.07 и нормативным документам на отдельные виды конструкций.
4.3.2 Расчет предварительно напряженных элементов по прогибам
4.3.2.1 Расчет изгибаемых элементов по прогибам производят из условия
f ≤ fult , (97)
где f - прогиб элемента от действия внешней нагрузки;
fult - значение предельно допустимого прогиба.
Прогибы изгибаемых предварительно напряженных элементов определяют по общим правилам строительной механики в зависимости от изгибных и сдвиговых деформационных характеристик железобетонного элемента в сечениях по его длине (кривизны, углов сдвига и т.д.).
В тех случаях когда прогибы элементов в основном зависят от изгибных деформаций, значения прогибов определяют по кривизнам элементов согласно пп. 4.3.2.2 - 4.3.2.4.
При действии
постоянных, длительных и кратковременных нагрузок прогиб балок или плит во всех
случаях не должен превышать ![]() пролета и
пролета и ![]() вылета консоли.
вылета консоли.
4.3.2.2 Прогиб предварительно напряженных элементов, обусловленный деформацией изгиба, определяют по формуле
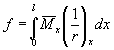 , (98)
, (98)
где ![]() - изгибающий
момент в сечении х от действия единичной силы, приложенной по
направлению искомого перемещения элемента в сечении по длине пролета l ,
для которого определяют прогиб;
- изгибающий
момент в сечении х от действия единичной силы, приложенной по
направлению искомого перемещения элемента в сечении по длине пролета l ,
для которого определяют прогиб;
![]() - полная кривизна элемента в сечении х от
внешней нагрузки, при которой определяют прогиб.
- полная кривизна элемента в сечении х от
внешней нагрузки, при которой определяют прогиб.
В общем случае
для железобетонных изгибаемых предварительно напряженных элементов вычисление
прогиба производят путем разбиения элемента на ряд участков, определения
кривизны на границах этих участков (с учетом отсутствия или наличия трещин и
знака кривизны) и перемножения эпюр моментов ![]() и кривизны
и кривизны ![]() по длине элемента при
линейном распределении кривизны в пределах каждого участка. В этом случае
прогиб в середине пролета элемента определяют по формуле
по длине элемента при
линейном распределении кривизны в пределах каждого участка. В этом случае
прогиб в середине пролета элемента определяют по формуле
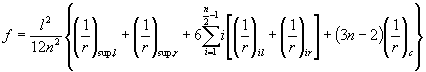 , (99)
, (99)
где ![]() - кривизна
элемента соответственно на левой и правой опорах;
- кривизна
элемента соответственно на левой и правой опорах;
![]() - кривизна элемента в симметрично
расположенных сечениях i и i ' ( i = i ')
соответственно слева и справа от оси симметрии (середины пролета);
- кривизна элемента в симметрично
расположенных сечениях i и i ' ( i = i ')
соответственно слева и справа от оси симметрии (середины пролета);
![]() - кривизна элемента в середине пролета;
- кривизна элемента в середине пролета;
п - четное число равных участков, на которые разделяют пролет, принимаемое не менее 6;
l - пролет элемента.
В формулах (98)
и (99) кривизну ![]() определяют по
указаниям п. 4.3.3 соответственно для
участков без трещин и с трещинами. Знак величины
определяют по
указаниям п. 4.3.3 соответственно для
участков без трещин и с трещинами. Знак величины ![]() принимают в
соответствии с эпюрой кривизны.
принимают в
соответствии с эпюрой кривизны.
4.3.2.3 Для изгибаемых предварительно напряженных элементов постоянного по длине элемента сечения, не имеющих трещин, прогибы определяют по общим правилам строительной механики с использованием жесткости поперечных сечений, определяемой по формуле (104).
4.3.2.4 Для изгибаемых предварительно напряженных элементов постоянного по длине элемента сечения, имеющих трещины, на каждом участке, в пределах которого изгибающий момент не меняет знак, кривизну допускается вычислять для наиболее напряженного сечения, принимая ее для остальных сечений такого участка изменяющейся пропорционально значениям изгибающего момента.
Для свободно опертых или консольных элементов максимальный прогиб определяют по формуле
![]() , (100)
, (100)
где S -
коэффициент, зависящий от расчетной схемы элемента и вида нагрузки,
определяемый по правилам строительной механики; при действии равномерно
распределенной нагрузки значение S принимают равным: ![]() - для свободно
опертой балки и
- для свободно
опертой балки и ![]() - для консольной
балки;
- для консольной
балки;
![]() - полная кривизна в сечении с наибольшим
изгибающим моментом от нагрузки, при которой определяют прогиб, вычисляемая
согласно п. 4.3.3.
- полная кривизна в сечении с наибольшим
изгибающим моментом от нагрузки, при которой определяют прогиб, вычисляемая
согласно п. 4.3.3.
4.3.3 Определение кривизны изгибаемых предварительно напряженных элементов
Общие положения
4.3.3.1 Кривизну изгибаемых предварительно напряженных элементов для вычисления их прогибов определяют:
а) для элементов или участков элемента, где в растянутой зоне не образуются нормальные к продольной оси трещины, - согласно пп. 4.3.3.2, 4.3.3.4;
б) для элементов или участков элемента, где в растянутой зоне имеются трещины, - согласно пп. 4.3.3.2, 4.3.3.3 и 4.3.3.5.
Элементы или участки элементов рассматривают без трещин, если трещины не образуются [т.е. условие (75) не выполняется] при действии полной нагрузки, включающей постоянную, временную длительную и кратковременную нагрузки, и усилия предварительного обжатия.
Кривизну железобетонных элементов с трещинами и без трещин можно также определять на основе деформационной модели согласно п. 4.3.4.
4.3.3.2 Полную кривизну изгибаемых предварительно напряженных элементов определяют по формулам:
- для участков без трещин в растянутой зоне
![]() ; (101)
; (101)
- для участков с трещинами в растянутой зоне
![]() . (102)
. (102)
В формуле (101):
![]() - кривизна соответственно от
непродолжительного действия кратковременных нагрузок и от продолжительного
действия постоянных и временных длительных нагрузок.
- кривизна соответственно от
непродолжительного действия кратковременных нагрузок и от продолжительного
действия постоянных и временных длительных нагрузок.
В формуле (102):
![]() - кривизна от непродолжительного действия
всей нагрузки, на которую производят расчет по деформациям;
- кривизна от непродолжительного действия
всей нагрузки, на которую производят расчет по деформациям;
![]() - кривизна от непродолжительного действия
постоянных и временных длительных нагрузок;
- кривизна от непродолжительного действия
постоянных и временных длительных нагрузок;
![]() - кривизна от продолжительного действия
постоянных и временных длительных нагрузок.
- кривизна от продолжительного действия
постоянных и временных длительных нагрузок.
Кривизну ![]() и
и ![]() в формулах (101),
(102) определяют согласно указаниям п. 4.3.3.3 с учетом усилия предварительного
обжатия в качестве длительной нагрузки.
в формулах (101),
(102) определяют согласно указаниям п. 4.3.3.3 с учетом усилия предварительного
обжатия в качестве длительной нагрузки.
Допускается при определении кривизны учитывать влияние деформаций усадки и ползучести бетона в стадии предварительного обжатия.
4.3.3.3 Кривизну изгибаемых
предварительно напряженных элементов ![]() от действия соответствующих
нагрузок ( п. 4.3.3.2) определяют по
формуле
от действия соответствующих
нагрузок ( п. 4.3.3.2) определяют по
формуле
![]() , (103)
, (103)
где М - изгибающий момент от внешней нагрузки;
N p и е0 p - усилие предварительного обжатия и его эксцентриситет относительно центра тяжести приведенного поперечного сечения элемента;
D - изгибная жесткость приведенного поперечного сечения элемента, определяемая по формуле
D = Eb1 Ired, (104)
где Е b 1 - модуль деформации сжатого бетона, определяемый в зависимости от продолжительности действия нагрузки;
Ired - момент инерции приведенного поперечного сечения относительно его центра тяжести, определяемый с учетом наличия или отсутствия трещин.
Значения модуля деформации бетона Е b 1 и момента инерции приведенного сечения Ired для элементов без трещин в растянутой зоне и с трещинами определяют соответственно по указаниям пп. 4.3.3.4 и 4.3.3.5.
Жесткость изгибаемого предварительно напряженного элемента на участке без трещин в растянутой зоне
4.3.3.4 Жесткость изгибаемого предварительно напряженного элемента D на участке без трещин определяют по формуле (104).
Момент инерции Ired приведенного поперечного сечения элемента относительно его центра тяжести определяют как для сплошного тела по общим правилам сопротивления упругих элементов с учетом всей площади сечения бетона и площадей сечения арматуры с коэффициентом приведения арматуры к бетону α.
Ired = I + Is α +I 's α , (105)
где I - момент инерции бетонного сечения относительно центра тяжести приведенного поперечного сечения элемента;
Is , Is ' - момент инерции площади сечения соответственно растянутой и сжатой арматуры относительно центра тяжести приведенного поперечного сечения элемента,
![]() ; (106)
; (106)
![]() ; (107)
; (107)
α - коэффициент приведения арматуры к бетону,
![]() , (108)
, (108)
ус - расстояние от наиболее сжатого волокна бетона до центра тяжести приведенного поперечного сечения элемента.
Значения I и ус определяют по общим правилам расчета геометрических характеристик сечений упругих элементов.
Допускается определять момент инерции Ired без учета арматуры.
В этом случае для прямоугольного сечения
![]() . (109)
. (109)
Значения модуля деформации бетона в формулах (104) и (108) принимают равными:
при непродолжительном действии нагрузки
![]() ; (110)
; (110)
при продолжительном действии нагрузки
![]() , (111)
, (111)
где φ b , cr - принимают по таблице 5.
Жесткость изгибаемого предварительно напряженного элемента на участке с трещинами в растянутой зоне
4.3.3.5 Жесткость изгибаемого предварительно напряженного элемента на участках с трещинами в растянутой зоне определяют с учетом следующих положений:
- сечения после деформирования остаются плоскими;
- напряжения в бетоне сжатой зоны определяют как для условно упругого тела;
- работу растянутого бетона в сечении с нормальной трещиной не учитывают;
- работу растянутого бетона на участке между смежными нормальными трещинами учитывают посредством коэффициента ψs .
Жесткость элемента D на участках с трещинами определяют по формуле (104).
Значения модуля деформации сжатого бетона Eb 1 принимают равными значениям приведенного модуля деформации Eb , red , определяемым по формуле (9) для соответствующих нагрузок (непродолжительного и продолжительного действия), заменяя Rb на Rb , ser .
Момент инерции приведенного поперечного сечения элемента Ired относительно его центра тяжести определяют по общим правилам сопротивления упругих элементов с учетом площади сечения бетона только сжатой зоны, площадей сечения арматуры, расположенной в сжатой зоне сечения, с коэффициентом приведения арматуры к бетону αs 1 и арматуры, расположенной в растянутой зоне сечения, с коэффициентом приведения арматуры к бетону αs 2
![]() , (112)
, (112)
где Ib , Is , I ' s - момент инерции площади сечения соответственно сжатой зоны бетона, арматуры, расположенной в растянутой и сжатой зоне, относительно центра тяжести приведенного без учета бетона растянутой зоны поперечного сечения.
Значения Is и I ' s определяют по формулам (106) и (107), принимая значение ус, равное расстоянию от наиболее сжатого волокна бетона до центра тяжести приведенного (с коэффициентами приведения αs 1 и αs 2 ) поперечного сечения без учета бетона растянутой зоны (рисунок 9).
Значения Ib и ус определяют по общим правилам расчета геометрических характеристик сечений упругих элементов.
Значения коэффициентов приведения арматуры к бетону αsl и αs 2 определяют по п. 4.3.3.8.
4.3.3.6 Для изгибаемых предварительно напряженных элементов положение нейтральной оси определяют из уравнения
![]() , (113)
, (113)
где yN - расстояние от нейтральной оси до точки приложения усилия предварительного обжатия N p ; точку приложения усилия N p определяют как для внецентренного сжатия с учетом изгибающего момента М от внешней нагрузки (рисунок 9);
Ib 0 , Is 0 , I ' s 0 , Sb 0, Ss 0 , S ' s 0 - моменты инерции и статические моменты соответственно сжатой зоны бетона, растянутой и сжатой арматуры относительно нейтральной оси.
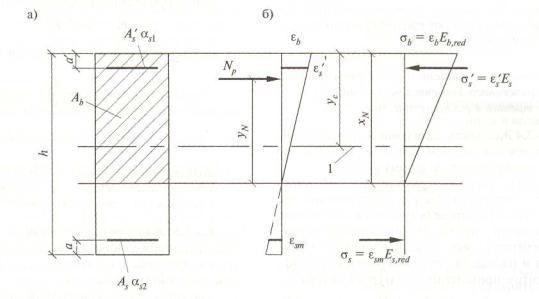
1 - уровень центра тяжести приведенного без учета растянутой зоны бетона поперечного сечения
Рисунок 9 - Приведенное поперечное сечение (а) и схема напряженно-деформированного состояния изгибаемого предварительно напряженного элемента с трещинами (б) при расчете его по деформациям
Допускается для элементов прямоугольного сечения высоту сжатой зоны определять по формуле
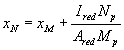 , (114)
, (114)
где х M - высота сжатой зоны изгибаемого элемента без учета предварительного напряжения арматуры, определяемая согласно СП 52-101;
Ired , Ared - момент инерции и площадь приведенного поперечного сечения, определяемые для полного сечения (без учета трещин);
Mp - момент относительно центра тяжести полного приведенного сечения элемента от внешней нагрузки M и усилия предварительного обжатия N p е0 p
Mp = M - Np e0p ;
e 0 p - эксцентриситет усилия обжатия N p относительно центра тяжести полного приведенного сечения элемента (без учета момента М).
Значения геометрических характеристик сечения элемента определяют по общим правилам расчета сечения упругих элементов.
4.3.3.7 Кривизну изгибаемых предварительно напряженных элементов допускается определять по формуле
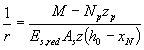 , (115)
, (115)
где zp - расстояние от точки приложения усилия предварительного обжатия до точки приложения равнодействующей усилий в сжатой зоне;
z - расстояние от центра тяжести растянутой арматуры до точки приложения равнодействующей усилий в сжатой зоне;
xN - высота сжатой зоны с учетом влияния предварительного обжатия.
Высоту сжатой
зоны определяют как для изгибаемых элементов без преднапряжения согласно СП
52-101 с умножением значения μ s на ![]() .
.
Значения zp и z допускается определять, принимая расстояние от точки приложения равнодействующей усилий в сжатой зоне до наиболее сжатого волокна сечения равным 0,3 h 0 .
4.3.3.8 Значения коэффициентов приведения арматуры к бетону принимают равными:
- для сжатой арматуры
![]() ; (116)
; (116)
- для растянутой арматуры
![]() , (117)
, (117)
где Е b , red - приведенный модуль деформации сжатого бетона, определяемый по формуле (9) при непродолжительном и продолжительном действии нагрузки с заменой Rb на Rb , ser ;
Es , red - приведенный модуль деформации растянутой арматуры, определяемый с учетом влияния работы растянутого бетона между трещинами по формуле
![]() . (118)
. (118)
Значения коэффициента ψ s определяют по формуле (96).
Допускается принимать ψ s = 1 и, следовательно, αs 2 = αs 1 . При этом, если условие (97) не удовлетворяется, расчет производят с учетом коэффициента ψ s по формуле (96).
4.3.4 Определение кривизны предварительно напряженных элементов на основе нелинейной деформационной модели
4.3.4.1 Полную кривизну изгибаемых предварительно напряженных элементов на участках без трещин в растянутой зоне сечения определяют по формуле (101), а на участках с трещинами в растянутой зоне сечения - по формуле (102).
Значения кривизны, входящие в формулы (101) и (102), определяют из решения системы уравнений (49) - (56) ( п. 3.1.4.4). При этом для элементов с нормальными трещинами в растянутой зоне напряжение в напрягаемой арматуре, пересекающей трещины, определяют по формуле
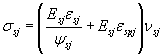 , (119)
, (119)
а в ненапрягаемой арматуре
![]() , (120)
, (120)
гд e 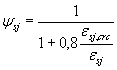 . (121)
. (121)
Здесь ε sj , crc - относительная деформация растянутой арматуры в сечении с трещиной от действия внешней нагрузки сразу после образования трещин;
esj - усредненная относительная деформация растянутой арматуры, пересекающей трещины, в рассматриваемой стадии;
е spj - относительная деформация предварительного напряжения арматуры.
При определении кривизны от непродолжительного действия нагрузки в расчете используют диаграммы кратковременного деформирования сжатого и растянутого бетона, а при определении кривизны от продолжительного действия нагрузки - диаграммы длительного деформирования бетона с расчетными характеристиками для предельных состояний второй группы.
5 к онструктивные требования
5.1 Общие положения
5.1.1 При проектировании предварительно напряженных железобетонных конструкций следует учитывать конструктивные требования СП 52-101, а также дополнительные конструктивные требования, приведенные ниже.
5.2 Защитный слой бетона
5.2.1 Толщину защитного слоя бетона арматуры предварительно напряженных элементов принимают не менее указанной в таблице 8.1 СП 52-101.
При этом у концов предварительно напряженных элементов на длине не менее 0,6 длины зоны передачи предварительного напряжения lp ( п. 2.2.3.11) следует предусматривать установку дополнительной поперечной или косвенной арматуры, охватывающей напрягаемую арматуру.
5.3 Анкеровка арматуры
5.3.1 Анкеровку напрягаемой арматуры осуществляют одним из следующих способов:
в виде прямого окончания стержня (прямая анкеровка);
с применением специальных анкерных устройств на конце стержня.
5.3.2 Базовую (основную) длину анкеровки напрягаемой арматуры, необходимую для передачи усилия в арматуре с полным расчетным значением сопротивления Rs на бетон, определяют по формуле
![]() , (122)
, (122)
где As и и s - соответственно площадь поперечного сечения анкеруемого стержня арматуры и периметр его сечения, определяемые по номинальному диаметру стержня;
Rbond - расчетное сопротивление сцепления арматуры с бетоном, принимаемое равномерно распределенным по длине анкеровки и определяемое по формуле
Rbond = η Rbt, (123)
здесь Rbt - расчетное сопротивление бетона осевому растяжению;
η - коэффициент, учитывающий влияние вида поверхности арматуры, принимаемый равным:
1.7 - для холоднодеформированной арматуры периодического профиля класса Вр1500 диаметром 3 мм и арматурных канатов класса К1500 диаметром 6 мм;
1.8 - для холоднодеформированной арматуры класса Вр диаметром 4 мм и более;
2,2 - для арматурных канатов класса К диаметром 9 мм и более;
2,5 - для горячекатаной и термомеханически обработанной арматуры класса А.
5.3.3 Требуемую расчетную длину прямой анкеровки напрягаемой арматуры с учетом конструктивного решения элемента в зоне анкеровки определяют по формуле
![]() , (124)
, (124)
но принимают не менее 15 ds и 200 мм.
В формуле (124):
l 0, an - базовая длина анкеровки, определяемая по формуле (122);
As , cal , As , ef - площадь поперечного сечения арматуры соответственно требуемая по расчету и фактически установленная.
Приложение А
Основные буквенные обозначения
|
Условия от внешних нагрузок и воздействий в поперечном сечении элемента |
||
|
М |
- изгибающий момент; |
|
|
М p |
- изгибающий момент с учетом момента усилия предварительного обжатия относительно центра тяжести приведенного сечения; |
|
|
Q |
- поперечная сила. |
|
|
Характеристики предварительно напряженного элемента |
||
|
P , Np |
- усилие предварительного обжатия с учетом потерь предварительного напряжения в арматуре, соответствующих рассматриваемой стадии работы элемента; |
|
|
P (1) , P (2) |
- усилие в напрягаемой арматуре с учетом соответственно первых и всех потерь предварительного напряжения; |
|
|
σ sp |
- предварительное напряжение в напрягаемой арматуре с учетом потерь предварительного напряжения в арматуре, соответствующих рассматриваемой стадии работы элемента; |
|
|
Δσ sp |
- потери предварительного напряжения в арматуре; |
|
|
σ bp |
- сжимающие напряжения в бетоне в стадии предварительного обжатия с учетом потерь предварительного напряжения в арматуре. |
|
|
Характеристики материалов |
||
|
Rb , n |
- нормативное сопротивление бетона осевому сжатию; |
|
|
Rb, Rb,ser |
- расчетное сопротивление бетона осевому сжатию для предельных состояний соответственно первой и второй групп; |
|
|
Rbt , n |
- нормативное сопротивление бетона осевому растяжению; |
|
|
Rbt, Rbt,ser |
- расчетное сопротивление бетона осевому растяжению для предельных состояний соответственно первой и второй групп; |
|
|
Rbp |
- передаточная прочность бетона; |
|
|
Rbond |
- расчетное сопротивление сцепления арматуры с бетоном; |
|
|
Rs, Rs,ser |
- расчетное сопротивление арматуры растяжению для предельных состояний соответственно первой и второй групп; |
|
|
Rsw |
- расчетное сопротивление поперечной арматуры растяжению; |
|
|
Rsc |
- расчетное сопротивление арматуры сжатию для предельных состояний первой группы; |
|
|
Eb |
- начальный модуль упругости бетона при сжатии и растяжении; |
|
|
Eb , red |
- приведенный модуль деформации сжатого бетона; |
|
|
Es |
- модуль упругости арматуры; |
|
|
Es , red |
- приведенный модуль деформации арматуры, расположенной в растянутой зоне элемента с трещинами; |
|
|
ε b 0 , εbt 0 |
- предельная относительная деформация бетона соответственно при равномерном осевом сжатии и осевом растяжении; |
|
|
ε s 0 |
- относительные деформации арматуры при напряжении, равном Rs ; |
|
|
ε b , sh |
- относительные деформации усадки бетона; |
|
|
φ b , cr |
- коэффициент ползучести бетона; |
|
|
α |
- отношение соответствующих модулей упругости арматуры Es и бетона Еь. |
|
|
Геометрические характеристики |
||
|
b |
- ширина прямоугольного сечения; ширина ребра таврового и двутаврового сечений; |
|
|
b ' f |
- ширина полки таврового и двутаврового сечений в сжатой зоне; |
|
|
h |
- высота прямоугольного, таврового и двутаврового сечений; |
|
|
h ' f |
- высота полки таврового и двутаврового сечений в сжатой зоне; |
|
|
a , a ' |
- расстояние от ближайшей грани сечения до равнодействующей усилий соответственно в растянутой и сжатой арматуре; |
|
|
h 0 |
- рабочая высота сечения, равная h - а; |
|
|
х |
- высота сжатой зоны бетона в предельном состоянии по прочности; |
|
|
xN |
- высота сжатой зоны при расчете по деформациям; |
|
|
ξ |
-
относительная высота сжатия зоны, равная |
|
|
sw |
- расстояние между хомутами, измеренное по длине элемента; |
|
|
е0 p |
- эксцентриситет усилия предварительного обжатия относительно центра тяжести приведенного сечения; |
|
|
yN |
- расстояние от нейтральной оси до точки приложения усилия предварительного обжатия с учетом изгибающего момента от внешней нагрузки; |
|
|
ер |
- расстояние от точки приложения усилия предварительного обжатия N p с учетом изгибающего момента от внешней нагрузки до центра тяжести растянутой или наименее сжатой арматуры; |
|
|
La п |
- длина зоны анкеровки; |
|
|
lp |
- длина зоны передачи предварительного напряжения в арматуре на бетон; |
|
|
ds , dsw |
- номинальный диаметр стержней соответственно продольной и поперечной арматуры; |
|
|
As , A ' s |
- площадь сечения арматуры, расположенной соответственно в растянутой и сжатой зонах сечения элемента; |
|
|
Asw |
- площадь сечения хомутов, расположенных в одной нормальной к продольной оси элемента плоскости, пересекающей наклонное сечение; |
|
|
А |
- площадь всего бетона в поперечном сечении; |
|
|
А bt |
- площадь сечения бетона растянутой зоны; |
|
|
Ared |
- площадь приведенного сечения элемента; |
|
|
I |
- момент инерции сечения всего бетона относительно центра тяжести сечения элемента; |
|
|
Ired |
момент инерции приведенного сечения элемента относительно его центра тяжести; |
|
|
W |
- момент сопротивления сечения элемента для крайнего растянутого волокна. |
|
Приложение Б
Перечень нормативных документов, на которые даны ссылки в тексте
СНиП 2.01.07-85* Нагрузки и воздействия
СНиП 23-01-99* Строительная климатология
СНиП 52-01-2003 Бетонные и железобетонные конструкции. Основные положения
СП 52-101-2003 Бетонные и железобетонные конструкции без предварительного напряжения арматуры
ГОСТ 14098-91 Соединения сварные арматуры и закладных изделий железобетонных конструкций. Типы, конструкции и размеры
РТМ 393-94 Руководящие технологические материалы по сварке и контролю качества соединений арматуры и закладных изделий железобетонных конструкций
|
Ключевые слова: материалы для предварительно напряженных железобетонных конструкций, расчет элементов по предельным состояниям первой и второй групп, конструктивные требования |