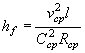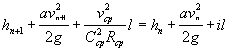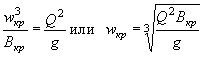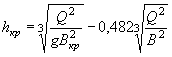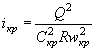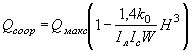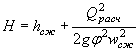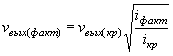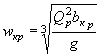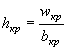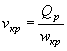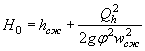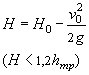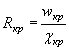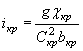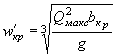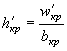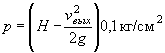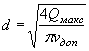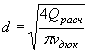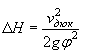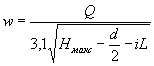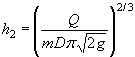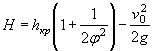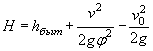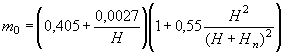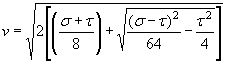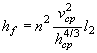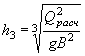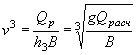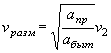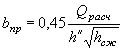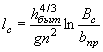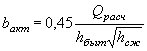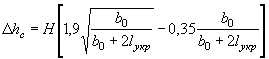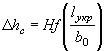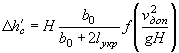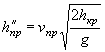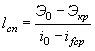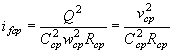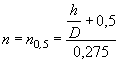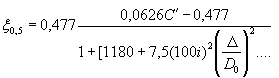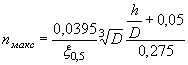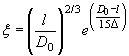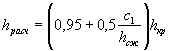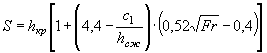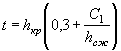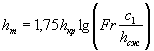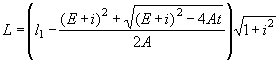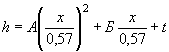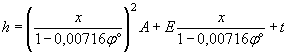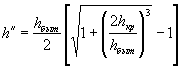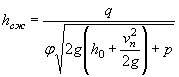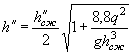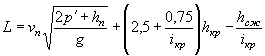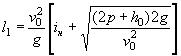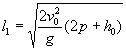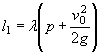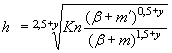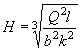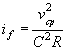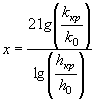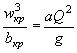Руководство Руководство по гидравлическим расчетам малых искусственных сооружений и русел
ГОСУДАРСТВЕННЫЙ ИНСТИТУТ ТЕХНИКО-ЭКОНОМИЧЕСКИХ ИЗЫСКАНИЙ И ПРОЕКТИРОВАНИЯ ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА
«ГИПРОТРАНСТЭИ» МПС
РУКОВОДСТВО ПО ГИДРАВЛИЧЕСКИМ РАСЧЕТАМ МАЛЫХ ИСКУССТВЕННЫХ СООРУЖЕНИЙ И РУСЕЛ
3-е ИЗДАНИЕ
(исправленное и переработанное)
Рекомендовано
Главтранспроектом Министерства транспортного строительства
в качестве пособия при проектировании
ИЗДАТЕЛЬСТВО «ТРАНСПОРТ»
Москва 1967
В книге приведены нормативы, принимаемые при гидравлических расчетах искусственных сооружений и русел, освещены методы расчета: труб при безнапорном, полунапорном и напорном режимах, отверстий мостов в различных условиях, нижнего бьефа при свободном, полусвободном и несвободном истечении в неразмываемое русло; размывов за укреплениями и при сливе с уступа. Кроме того, освещаются гидравлические расчеты косогорных сооружений - труб, водобойных колодцев и подпорных стен, а также расчеты канав и фильтрующих насыпей.
Книга является пособием для проектировщиков - путейцев и строителей.
Таблиц 32, иллюстраций 141, библиографий 17, приложений 35.
СОДЕРЖАНИЕ
|
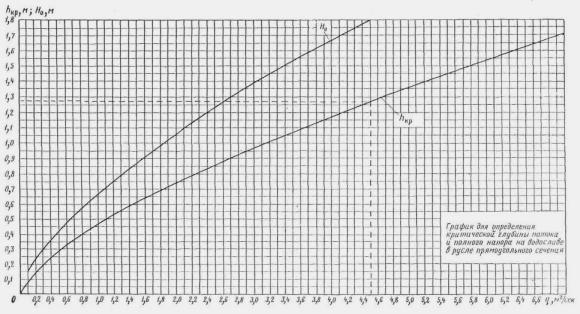
ПРЕДИСЛОВИЕ ГЛАВА I ОСНОВНЫЕ ПОЛОЖЕНИЯ ОБЩИЕ ПОЛОЖЕНИЯ ОСНОВНЫЕ РАСЧЕТНЫЕ ЗАВИСИМОСТИ РАВНОМЕРНОЕ ДВИЖЕНИЕ ПОТОКА НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ ПОТОКА ГЛАВА II РАСЧЕТЫ ТРУБ. БЕЗНАПОРНЫЕ И ПОЛУНАПОРНЫЕ ТРУБЫ ОБЩИЕ ПОЛОЖЕНИЯ УПРОЩЕННЫЙ РАСЧЕТ ОТВЕРСТИЙ ТРУБ С УЧЕТОМ АККУМУЛЯЦИИ ПРИМЕР РАСЧЕТА ОТВЕРСТИЙ ТРУБ С УЧЕТОМ АККУМУЛЯЦИИ ПРОЧИЕ СЛУЧАИ РАСЧЕТА ТРУБ РАСЧЕТ БЕЗНАПОРНЫХ ТРУБ ПРИ ЗАТОПЛЕННОМ СЖАТОМ СЕЧЕНИИ РАСЧЕТ БЕЗНАПОРНЫХ ТРУБ ПРИ УКЛОНЕ, МЕНЬШЕМ КРИТИЧЕСКОГО РАСЧЕТ БЕЗНАПОРНЫХ ТРУБ ПРИ УКЛОНЕ, БОЛЬШЕМ КРИТИЧЕСКОГО РАСЧЕТ ТРУБ С ЗАТОПЛЕННЫМ ВХОДНЫМ ОТВЕРСТИЕМ (ПОЛУНАПОРНЫХ) НАПОРНЫЕ ТРУБЫ Общие положения Общий метод расчета Расчет напорных труб при затопленном нижнем бьефе ОСОБЫЕ СЛУЧАИ РАСЧЕТА ТРУБ Поверочные расчеты по наибольшему расходу Qм aк c Расчет дюкеров Расчет приемного шахтного водосброса ГЛАВА III РАСЧЕТЫ МОСТОВ ОБЩИЕ ПОЛОЖЕНИЯ РАСЧЕТЫ ОТВЕРСТИЙ МОСТОВ В ОБЫЧНЫХ УСЛОВИЯХ ПОВЕРОЧНЫЕ РАСЧЕТЫ ОТВЕРСТИЙ СУЩЕСТВУЮЩИХ МОСТОВ НОМОГРАММЫ ДЛЯ РАСЧЕТА ОТВЕРСТИЙ МОСТОВ ТРАПЕЦЕИДАЛЬНОГО СЕЧЕНИЯ ЧАСТНЫЕ СЛУЧАИ РАСЧЕТА МОСТОВ. МНОГОПРОЛЕТНЫЕ МОСТЫ ОПРЕДЕЛЕНИЕ ОТВЕРСТИЙ МОСТОВ НА ЗАЛИВАХ ВОДОХРАНИЛИЩ Многопутные мосты АРОЧНЫЕ МОСТЫ МОСТЫ-ВОДОСПУСКИ ОПРЕДЕЛЕНИЕ ОТВЕРСТИЙ ИСКУССТВЕННЫХ СООРУЖЕНИЙ НА СОРОВЫХ УЧАСТКАХ ТРАССЫ ГЛАВА IV РАСЧЕТЫ ОТВЕРСТИЙ МАЛЫХ МОСТОВ И ТРУБ С УЧЕТОМ АККУМУЛЯЦИИ ОБЩИЕ ПОЛОЖЕНИЯ УПРОЩЕННАЯ ФОРМУЛА (ПРИ РАСЧЕТАХ ПО СНЕГОВОМУ СТОКУ) ГРАФО-АНАЛИТИЧЕСКИЙ РАСЧЕТ АККУМУЛЯЦИИ ВЕСЕННЕГО СТОКА ГРАФО-АНАЛИТИЧЕСКИЙ МЕТОД РАСЧЕТА ГЛАВА V РАСЧЕТЫ НИЖНЕГО БЬЕФА ОБЩИЕ ПОЛОЖЕНИЯ РАСЧЕТЫ ПРИ СВОБОДНОМ ИСТЕЧЕНИИ В НЕРАЗМЫВАЕМОЕ РУСЛО РАСЧЕТЫ ПРИ ПОЛУСВОБОДНОМ И НЕСВОБОДНОМ ИСТЕЧЕНИИ В НЕРАЗМЫВАЕМОЕ РУСЛО РАСЧЕТЫ РАЗМЫВОВ ЗА УКРЕПЛЕНИЯМИ РАСЧЕТЫ РАЗМЫВА ПРИ СЛИВЕ С УСТУПА Конструктивные расчеты ГЛАВА VI РАСЧЕТЫ КОСОГОРНЫХ СООРУЖЕНИЙ ОБЩИЕ ПОЛОЖЕНИЯ БЫСТРОТОКИ РАСЧЕТ БЫСТРОТОКОВ ИСКУССТВЕННАЯ ШЕРОХОВАТОСТЬ КОСОГОРНАЯ ТРУБА ВЫХОДНЫЕ УСТРОЙСТВА ГАСИТЕЛЬ КОНСТРУКЦИИ ЦНИИСа РАСШИРЯЮЩИЙСЯ КОЛОДЕЦ РАСЧЕТ ВОДОБОЙНЫХ КОЛОДЦЕВ РАСЧЕТ ВОДОБОЙНОЙ СТЕНКИ РАСЧЕТ КОМБИНИРОВАННОГО ВОДОБОЙНОГО КОЛОДЦА РАСЧЕТЫ ПРЯМОУГОЛЬНЫХ ВОДОБОЙНЫХ КОЛОДЦЕВ И ВОДОБОЙНЫХ СТЕНОК ПО УПРОЩЕННОМУ СПОСОБУ акад. Е.А. ЗАМАРИНА ПЕРЕПАДЫ ОДНОСТУПЕНЧАТЫЙ ПЕРЕПАД МНОГОСТУПЕНЧАТЫЙ ПЕРЕПАД МНОГОСТУПЕНЧАТЫЙ ПЕРЕПАД КОЛОДЕЗНОГО ТИПА КОНСОЛЬНЫЙ ВОДОСБРОС РАСЧЕТ ОТВОДНОГО РУСЛА ГЛАВА VII РАСЧЕТЫ КАНАВ ОБЩИЕ ПОЛОЖЕНИЯ ОБЩИЙ МЕТОД РАСЧЕТА КАНАВ ПРИБЛИЖЕННЫЙ МЕТОД РАСЧЕТА КАНАВ ГРАФО-АНАЛИТИЧЕСКИЕ МЕТОДЫ РАСЧЕТА КАНАВ 1. По номограммам Павловского 2. По номограмме Спивакова-Иоффе 3. По графикам Промтранспроекта ТАБЛИЦЫ ДЛЯ РАСЧЕТА КАНАВ (ТАБЛ. VII.4- VII.7) ГЛАВА VIII ФИЛЬТРУЮЩИЕ НАСЫПИ И БРОДЫ РАСЧЕТ НАПОРНЫХ ФИЛЬТРУЮЩИХ НАСЫПЕЙ РАСЧЕТ БЕЗНАПОРНЫХ ФИЛЬТРУЮЩИХ НАСЫПЕЙ ГИДРАВЛИЧЕСКИЙ РАСЧЕТ БРОДОВ ПРИЛОЖЕНИЯ ОСНОВНЫЕ ГИДРАВЛИЧЕСКИЕ ПОНЯТИЯ ЗНАЧЕНИЕ БУКВ И РАЗМЕРНОСТЬ ВЕЛИЧИН, ВСТРЕЧАЮЩИХСЯ В РУКОВОДСТВЕ ОСНОВНЫЕ ГИДРАВЛИЧЕСКИЕ ФОРМУЛЫ ВРЕМЕННЫЕ НОРМЫ ДОПУСКАЕМЫХ СКОРОСТЕЙ ТЕЧЕНИЯ ВОДЫ В ПОСТОЯННЫХ ЕЛЕЗНОДОРОЖНЫХ ГИДРОТЕХНИЧЕСКИХ СООРУЖЕНИЯХ, КОЭФФИЦИЕНТЫ ГИДРАВЛИЧЕСКОЙ ШЕРОХОВАТОСТИ n К ФОРМУЛАМ ПАВЛОВСКОГО ЗНАЧЕНИЯ КОЭФФИЦИЕНТА С ПО ФОРМУЛЕ ПАВЛОВСКОГО График коэффициента С по формуле Павловского График для определения глубины воды при равномерном движении в прямоугольном русле (п = 0,016) График для определения критической глубины потока и полного напора на водосливе в русле прямоугольного сечения График для определения расчетной длины кривой спада в призматическом русле прямоугольного сечения График для построения кривой свободной поверхности в призматическом русле.( n = 0,016) ГИДРАВЛИЧЕСКИЕ КОЭФФИЦИЕНТЫ ПЛОЩАДЬ ЖИВОГО СЕЧЕНИЯ Kw И ГИДРАВЛИЧЕСКИЙ РАДИУС KR ЧАСТИЧНО НАПОЛНЕННЫХ КРУГЛЫХ ТРУБ (ПРИ D = 1) ПРОПУСКНАЯ СПОСОБНОСТЬ КРУГЛЫХ ТРУБ ГИДРАВЛИЧЕСКИЕ ХАРАКТЕРИСТИКИ ТИПОВЫХ КРУГЛЫХ ЖЕЛЕЗОБЕТОННЫХ ТРУБ ГИДРАВЛИЧЕСКИЕ ХАРАКТЕРИСТИКИ ТИПОВЫХ ПРЯМОУГОЛЬНЫХ ЖЕЛЕЗОБЕТОННЫХ ТРУБ ЗНАЧЕНИЕ КОЭФФИЦИЕНТА m0 ДЛЯ ВОДОСЛИВА С ТОНКОЙ СТЕНКОЙ ГРАФИКИ ПРОПУСКНОЙ СПОСОБНОСТИ ТРУБ ДЛЯ РАСЧЕТА ОТВЕРСТИЙ С УЧЕТОМ АККУМУЛЯЦИИ Круглые одноочковые трубы диаметром 1,0-2,0 м с коническими входными и выходными звеньями под железную и автомобильную дороги Круглые ДВУХочковые трубы диаметром 1,0-2,0 м с коническими входными и выходными звеньями под железную и автомобильную дороги Круглые ТРЕХочковые трубы диаметром 1,0-2,0 м с коническими входными и выходными звеньями под железную и автомобильную дороги Прямоугольные трубы с повышенными входными звеньями отверстиями 1,0 м, 1,25 м и 1,5 м под железную дорогу Прямоугольные трубы отверстиями 2,0 м, 2,5, 3 и 4 м под железную и автомобильную дороги Прямоугольные двухочковые трубы отверстиями 2×2, и 2×2,5 м, 2×3 и 2×4 м под железную и автомобильную дороги Прямоугольные двухочковые трубы с повышенными входными звеньями отверстиями 1,25 м и 1,5 м под железную дорогу График для определения площади живого сечения в круглой трубе График для определения гидравлического радиуса в круглой трубе График для определения смоченного периметра в круглой трубе ГРАФИК ДЛЯ ОПРЕДЕЛЕНИЯ КРИТИЧЕСКОЙ ГЛУБИНЫ В КРУГЛОЙ ТРУБЕ ТИПЫ КОНСТРУКЦИЙ ПОВЫШЕННОЙ ШЕРОХОВАТОСТИ ГРАФИК ДЛЯ ОПРЕДЕЛЕНИЯ СЖАТОЙ ГЛУБИНЫ И СОПРЯЖЕННОЙ С НЕЙ В РУСЛАХ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ ГИДРАВЛИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПРЯМОУГОЛЬНЫХ, ТАВРОВЫХ И ДВУХСТРУйНЫХ ОЛОДЦЕВ НА ВХОДЕ (СО СТЕНКОЙ ПАДЕНИЯ) Гидравлические данные для лотков на организованных руслах Гидравлические данные для лотков на организованных руслах (инв.№ 160) Гидравлические данные для лотков на неорганизованных руслах Гидравлические данные для лотков на неорганизованных руслах (инв.№ 160) ЛИТЕРАТУРА
|
ПРЕДИСЛОВИЕ
За пять лет после выхода в свет 2-го издания Руководства по гидравлическим расчетам малых искусственных сооружений и русел разработан ряд нормативных документов по расчету отверстий малых мостов и труб и проведены значительные научно-исследовательские работы в области гидравлики искусственных сооружений.
Так, при разработке типового проекта унифицированных водопропускных труб кафедрой гидравлики Ленинградского политехнического института выполнены специальные научные исследования по заказу Ленгипротрансмоста; для типового проекта косогорных сооружений ЦНИИСом Минтрансстроя также проведены значительные исследования; проектными организациями (Харгипротрансом, Киевгипротрансом, Мосгипротрансом и другими) составлен ряд графиков и номограмм.
Эти обстоятельства вызвали необходимость подготовки 3-го издания Руководства, при которой были учтены замечания по 2-му изданию, полученные от Ленгипротранса, Сибгипротранса, Мосгипротранса (инж. Л.Л. Лиштвана), Дальгипротранса, Киевгипротранса (канд. техн. наук О.А. Рассказова), Ленгипротрансмоста, ЦНИИСа, Союздорпроекта, НИИЖТа, БИИЖТа, а также кандидатов технических наук Л.Г. Рабухина, Э.А. Гарбовского и П.С. Крутенкова.
В соответствии с указанными выше разработками и исследованиями, а также с учетом присланных замечаний Руководство подверглось существенной переработке; особенно значительные изменения внесены в главы II «Расчеты труб» и VI «Косогорные сооружения».
Глава II дополнена материалами, необходимыми для проверки отверстий существующих труб, для расчетов труб с учетом аккумуляции и определения увеличения водопропускной способности труб за счет устройства обтекаемых открылков.
Глава IV полностью переработана старшим научным сотрудником ЦНИИСа Н. Н. Чегодаевым.
В основу главы VI положена работа ЦНИИСа «Методические указания по гидравлическим расчетам косогорных труб» и составленное Ленгипротрансмостом проектное задание на унифицированные косогорные водопропускные трубы.
Третье издание Руководства подготовлено в Отделе дорпроектов Гипротранстэи в составе работ по методической помощи дорпроектам железных дорог главным специалистом Л. В. Бутковым и руководителем бригады Б.О. Зак.
В окончательном редактировании приняли участие на общественных началах кандидаты технических наук О.В. Андреев и М.И. Виноградов.
Начальник Гипротранстэи МПС А.Ф. СЕМЕНЯКО
ГЛАВА I
ОСНОВНЫЕ ПОЛОЖЕНИЯ
ОБЩИЕ ПОЛОЖЕНИЯ
В руководстве излагаются принципы гидравлических расчетов малых искусственных сооружений - мостов и труб, а также канав и косогорных сооружений (малыми мостами условно называются мосты длиной не более 25 м).
Предполагается, что в результате произведенных ранее гидрологических расчетов (см. «Инструкцию по расчету стока с малых бассейнов») определены соответствующие расчетные расходы воды Q pacx, а также наибольшие расходы Qмакс.
Для железных дорог общей сети и подъездных путей, не связанных с технологическими перевозками, расчеты мостов, труб и пойменных насыпей на воздействие водного потока должны производиться по двум расходам воды и соответствующим им уровням - по расчетному и наибольшему.
Искусственные сооружения на остальных подъездных путях промышленных предприятий, на автомобильных дорогах, а также все водоотводные канавы нужно рассчитывать только по расчетным расходам и соответствующим им уровням (табл. 1.1).
Таблица 1.1
Нормы вероятностей превышения расчетных и наибольших расходов
для железных дорог колеи 1524 мм
|
Род сооружения |
Категория дороги |
Вероятность превышения расходов в % |
|
|
расчетного |
наибольшего |
||
|
Мосты и трубы |
I и II общей сети, а также подъездные пути, не связанные с технологическими перевозками |
1 |
0,3 |
|
То же |
Ниже II общей сети и все категории промышленных предприятий |
2 |
0,3 |
|
Железные дороги колеи 750 мм |
|||
|
Мосты и трубы |
I и II |
2 |
1 |
|
То же |
III |
3 |
2 |
|
Мосты и трубы с ограниченным сроком службы |
- |
5 |
- |
|
Автомобильные и городские дороги |
|||
|
Мосты |
I , II и III общей сети и городские |
1 |
- |
|
» |
Ниже III общей сети и все категории промышленных предприятий |
2 |
- |
|
Трубы |
I |
1 |
- |
|
» |
II и III общей сети, все городские и промышленные предприятия |
2 |
- |
|
Малые деревянные мосты и трубы |
Ниже III общей сети |
3 |
- |
Расчет отверстий мостов на малых водотоках и труб следует производить по расходам, имеющим вероятности превышения, указанные в табл. 1.1, и средним допускаемым скоростям течения воды (обеспечивающим нормальные условия эксплуатации) в зависимости от характера грунта и типа укрепления русла и конусов, а также по допускаемым возвышениям, низа конструкции сооружения и бровки насыпей подходов.
На железных дорогах для мостов на малых водотоках и для труб при расчете на пропуск наибольшего расхода допускаемые скорости повышаются для мостов на 20 и для труб на 35 %.
В результате гидравлических расчетов должны быть получены основные гидравлические параметры сооружения, определяющие его конструктивные характеристики, а именно:
а) подпор перед сооружением Н, по величине которого можно судить о том, затоплено или нет входное отверстие сооружения и достаточна ли высота насыпи;
б) глубина воды в сооружении h, которая показывает, соблюдены ли нормы технических условий в отношении предельно допускаемого затопления отверстия;
в) скорость течения на выходе из сооружения vвых и глубина hвых для выбора мероприятий по защите русла от размывов. (Допускаемые скорости воды даны в приложении 4).
Бровка земляного полотна на подходах к малым мостам и трубам должна возвышаться не менее чем на 0,5 м над отметкой подпертого уровня (соответствующего наибольшему расходу для железных дорог общего пользования и расчетному расходу для всех прочих дорог) при безнапорном режиме и не менее чем на 1 м для труб отверстием 2 м и более при напорном и полунапорном режимах.
На каждом пересечении водотока железной или автомобильной дорогой, как правило, должно быть предусмотрено одно водопропускное сооружение.
Пропуск воды нескольких соседних водотоков через одно сооружение можно проектировать при технико-экономическом обосновании с учетом условий эксплуатации, а при легкоразмываемых грунтах и на косогорах - только в отдельных случаях при условии надежной защиты полотна и русла от размыва.
При необходимости устройства временных мостов и труб, предназначенных для пропуска воды во время строительства или для других целей, отверстия их рассчитываются по расчетным расходам десятилетней вероятности превышения.
Мосты и трубы промышленных предприятий со сроком службы менее 20 лет рассчитываются по расчетным расходам с повторяемостью один раз в 33 г.
Устраивать срезку под временными мостами нужно только в тех случаях, когда она согласуется со срезкой, предусмотренной проектом основного сооружения.
Отверстия временных труб могут назначаться от 0,5 до 1,5 м. При необходимости устройства труб большего отверстия целесообразнее предусматривать временные мосты.
При необходимости временного пропуска малых расходов (примерно до 3 м3/сек) вместо временных мостов и труб можно устраивать фильтрующие сооружения, причем разрешается не производить проверку их на заиливание.
Постоянные фильтрующие насыпи и комбинированные фильтрующие сооружения допускается применять только на железных дорогах III и IV категорий и автомобильных дорогах III, IV и V категорий при малых расходах воды и незначительном количестве взвешенных частиц в потоке.
Селепропускные сооружения предпочтительнее назначать в виде однопролетных мостов отверстием не менее 4 м или селеспусков при минимальном стеснении потока. Применение в этих условиях труб отверстием менее 4 м не допускается.
При трассировании железнодорожной линии или автодороги по равнине вблизи возвышенностей или горных цепей русла малых периодических водотоков по выходе с гор или полностью бесприточны, или приток к ним с равнинных частей не совпадает во времени с основным стоком горной части бассейна. И в том, и в другом случае русла горных водотоков по выходе их на равнину являются транзитными (рис. 1.1).
Рис. 1.1 Транзитные русла водотоков
В этих случаях отверстия малых искусственных сооружений следует рассчитывать по уменьшенному вследствие распластывания паводочной волны расходу Qi, определяемому по формуле
Qi = Q χP,
где коэффициент χP определяется по методу и графикам Л.Л. Лиштвана (рис. 1.2) в зависимости от уклона транзитного русла i и длины его l, а также времени подъема паводка
![]() ,
,
где W - объем паводка в м3. Канавы нужно рассчитывать по расходам воды с вероятностью превышения: для железных дорог I категории - 2 %, II категории - 4 %, III и IV категорий и узкоколейных - 5 %.
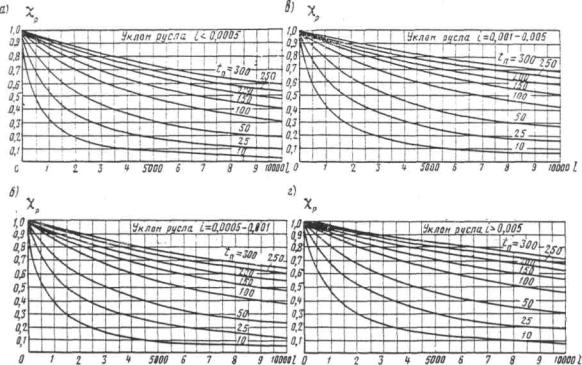
Рис. 1.2. Графики Л.Л. Лиштвана
При объединении водотоков общий расчетный расход определяется следующим образом:
а) если расчетный расход всех объединяемых водотоков определяется снеговым стоком, за расчетный расход для сооружения принимается суммарный расход водотоков;
б) если расчетный расход этих водотоков определяется ливневым стоком, то за расчетный расход для сооружения принимается расход, определяемый по формуле
![]() ,
,
где ![]() - расход того
бассейна, на котором располагается данное сооружение;
- расход того
бассейна, на котором располагается данное сооружение;
![]() - суммарный
расход смежных бассейнов, отводимый в данное сооружение;
- суммарный
расход смежных бассейнов, отводимый в данное сооружение;
К - коэффициент, учитывающий неравномерность выпадения осадков на объединяемых бассейнах, разность во времени добегания паводка к сооружению с объединяемых бассейнов, а также впитывание и распластывание паводочной волны на протяжении транзитных русел. Ориентировочно можно принимать К = 0,75. В особо сложных ответственных случаях суммирование отводных ливневых расходов производится с учетом разности во времени добегания и распластывания паводков объединяемых бассейнов путем построения гидрографов. При переливах из одного бассейна в другой расчетные расходы для расчета отверстий сооружений принимаются:
для сооружения на том бассейне, из которого переливается
вода, - равными расходу данного бассейна ![]() или
или ![]() без учета
сброса части расхода ΔQ11
без учета
сброса части расхода ΔQ11
для сооружения на том бассейне, в который поступает дополнительная вода, - равными сумме расхода данного бассейна Q1 и части расхода смежного бассейна ΔQ11
Для определения ΔQ11 необходимо произвести дополнительные гидрологические обследования и гидравлические расчеты; определить бытовую глубину и скорость течения водотока у места перелива, живое сечение в пределах перелива и на их основе - долю расхода, сбрасываемого в данный бассейн.
Путем сброса части стока от искусственных сооружений, у которых нельзя создать значительную аккумуляцию воды, к сооружениям, где аккумуляция возможна, удается снижать величины отверстий первых искусственных сооружений без увеличения (или с незначительным увеличением) отверстий вторых сооружений.
ОСНОВНЫЕ РАСЧЕТНЫЕ ЗАВИСИМОСТИ
Для установившегося медленно изменяющегося движения потока основными формулами являются: формула неразрывности потока (1.1), формула Шези для определения средней скорости (1.2) и уравнение Бернулли (1.7):
|
Q = wv = const (вдоль потока), |
(1.1) |
где Q - расход потока;
![]() - площадь
живого сечения потока;
- площадь
живого сечения потока;
![]() - средняя
скорость потока в данном живом сечении.
- средняя
скорость потока в данном живом сечении.
Формула Шези для определения средней скорости по сечению
|
|
(1.2) |
где i - гидравлический уклон (уклон поверхности водотока),
|
|
(1.3) |
С - коэффициент Шези, имеющий размерность ![]()
![]()
Коэффициент Шези С рекомендуется вычислять по формуле Н.Н. Павловского
|
|
(1.4) |
где п - коэффициент шероховатости, значения которого приведены в приложении 5;
|
|
(1.5) |
![]() -
смоченный периметр.
-
смоченный периметр.
Для русел при B = 10 hср можно принимать R ≈ hср.
Показатель степени у в формуле Павловского определяется по формуле
|
|
(1.6) |
Эта зависимость действительна при значениях 0,1 £ R £ 3 м и п = 0,011 ¸0,040. Приближенно формулу (1.5) можно заменить более простыми выражениями:
а) при R < 1 м y » 1,5 ![]() ;
;
б) при R > 1 м y » 1,3 ![]() .
.
Значения коэффициента С по формуле Павловского даны в приложениях 6 и 7.
Для приближенных практических расчетов в соответствии с рекомендациями проф. М.Д. Чертоусова у принимается постоянным:
у = 1/6 при 0,010 £ n £ 0,015;
у = 1/5 при 0,015 £ n £ 0,025;
у = 1/4 при п ³ 0,025.
Уравнение Бернулли для потока при медленно изменяющемся движении в нем:
|
|
(1.7) |
где Z1, Z2 - отметки какой-либо характерной точки живого сечения (например, дна);
р - давление в характерной точке живого сечения;
![]() - удельная
энергия давления или пьезометрическая высота;
- удельная
энергия давления или пьезометрическая высота;
γ - вес единицы объема жидкости;
![]() - удельная
кинетическая энергия, или скоростной напор;
- удельная
кинетическая энергия, или скоростной напор;
а - коэффициент, учитывающий неравномерность распределения скоростей по сечению.
Н.Н. Павловский рекомендует в обыкновенных условиях при равномерном движении в каналах принимать а = 1,1;
hw - общие потери напора потока между первым и вторым сечениями
|
|
(1.8) |
hr - местные потери напора (крутые повороты, резкие изменения сечения и т. д.);
|
|
(1.9) |
z - коэффициент местного сопротивления, определяется по любому курсу или справочнику Гидравлики;
ht - потери напора по длине потока (потери напора на трение)
|
|
(1.10) |
где l - расстояние между сечениями;
vcp; Сср; Rcp-среднеарифметические значения этих величин между сечениями 1 и 2.
Таблица 1.2
Таблица значений функций П (Пн) в зависимости от модулей расходов (для прямоугольных русел) при i0>0
|
|
П(Пн ) |
|
П(Пн) |
|
П(Пн) |
|
П(Пн) |
|
П(Пн) |
|
0 |
0 |
0,77 |
1,020 |
0,980 |
2,297 |
1,20 |
1,199 |
1,49 |
0,813 |
|
0,05 |
0,05 |
0,78 |
1,045 |
0,985 |
2,442 |
1,21 |
1,177 |
1,50 |
0,805 |
|
0,10 |
0,10 |
0,79 |
1,071 |
0,990 |
2,646 |
1,22 |
1,156 |
1,55 |
0,767 |
|
0,15 |
0,151 |
0,80 |
1,098 |
0,995 |
3,000 |
1,23 |
1,136 |
1,60 |
0,733 |
|
0,20 |
0,202 |
0,81 |
1,127 |
1,000 |
- |
1,24 |
1,117 |
1,65 |
0,703 |
|
0,25 |
0,255 |
0,82 |
1,156 |
1,005 |
2,997 |
1,25 |
1,098 |
1,70 |
0,675 |
|
0,30 |
0,309 |
0,83 |
1,188 |
1,010 |
2,652 |
1,26 |
1,081 |
1,75 |
0,650 |
|
0,35 |
0,365 |
0,84 |
1,221 |
1,015 |
2,450 |
1,27 |
1,065 |
1,80 |
0,626 |
|
0,40 |
0,423 |
0,85 |
1,256 |
1,020 |
2,307 |
1,28 |
1,049 |
1,85 |
0,605 |
|
0,45 |
0,484 |
0,86 |
1,293 |
1,025 |
2,197 |
1,29 |
1,033 |
1,90 |
0,585 |
|
0,50 |
0,549 |
0,87 |
1,333 |
1,030 |
2,107 |
1,30 |
1,018 |
1,95 |
0,507 |
|
0,55 |
0,619 |
0,88 |
1,375 |
1,035 |
2,031 |
1,31 |
1,004 |
2,00 |
0,550 |
|
0,60 |
0,693 |
0,89 |
1,421 |
1,040 |
1,966 |
1,32 |
0,990 |
2,10 |
0,518 |
|
0,61 |
0,709 |
0,90 |
1,472 |
1,045 |
1,908 |
1,33 |
0,977 |
2,20 |
0,490 |
|
0,62 |
0,725 |
0,905 |
1,499 |
1,050 |
1,857 |
1,34 |
0,964 |
2,30 |
0,466 |
|
0,63 |
0,741 |
0,910 |
1,527 |
1,06 |
1,768 |
1,35 |
0,952 |
2,40 |
0,444 |
|
0,64 |
0,758 |
0,915 |
1,557 |
1,07 |
1,693 |
1,36 |
0,940 |
2,50 |
0,424 |
|
0,65 |
0,775 |
0,920 |
1,589 |
1,08 |
1,629 |
1,37 |
0,928 |
2,60 |
0,405 |
|
0,66 |
0,792 |
0,925 |
1,622 |
1,09 |
1,573 |
1,38 |
0,917 |
2,70 |
0,389 |
|
0,67 |
0,810 |
0,930 |
1,658 |
1,10 |
1,522 |
1,39 |
0,906 |
2,80 |
0,374 |
|
0,68 |
0,829 |
0,935 |
1,696 |
1,11 |
1,477 |
1,40 |
0,896 |
2,90 |
0,360 |
|
0,69 |
0,848 |
0,940 |
1,738 |
1,12 |
1,436 |
1,41 |
0,886 |
3,00 |
0,346 |
|
0,70 |
0,867 |
0,945 |
1,782 |
1,13 |
1,398 |
1,42 |
0,876 |
3,50 |
0,294 |
|
0,71 |
0,887 |
0,950 |
1,831 |
1,14 |
1,368 |
1,43 |
0,866 |
4,00 |
0,255 |
|
0,72 |
0,907 |
0,955 |
1,885 |
1,15 |
1,331 |
1,44 |
0,856 |
4,50 |
0,226 |
|
0,73 |
0,928 |
0,960 |
1,945 |
1,16 |
1,301 |
1,45 |
0,847 |
5,00 |
0,203 |
|
0,74 |
0,950 |
0,965 |
2,013 |
1,17 |
1,273 |
1,46 |
0,838 |
6,00 |
0,168 |
|
0,75 |
0,972 |
0,970 |
2,092 |
1,18 |
1,247 |
1,47 |
0,829 |
8,00 |
0,126 |
|
0,76 |
0,996 |
0,975 |
2,184 |
1,19 |
1,222 |
1,48 |
0,821 |
10,00 |
0,100 |
Для упрощения операций по построению кривых свободной поверхности различными авторами разработаны практические приемы построения кривой свободной поверхности потока в призматическом русле и составлены таблицы и графики для ускорения расчетов. Один из таких приемов по способу Н.Н. Павловского излагается ниже.
Сущность этого приема заключается в следующем: расстояние между сечениями с глубиной hн и hi определяется по формуле
|
|
(1.11) |
где, ![]() и
и ![]()
![]() ;
;
![]() ;
;
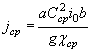 ;
;
![]()
Пн и П(Пн) следует
определять в зависимости от отношения модулей расходов ![]() по табл. 1.2 (по этой
же таблице, подставляя вместо КнК1;
определяются П1 и П(П1). При необходимости
построения кривой свободной поверхности потока в русле переменной ширины может
быть использован прием проф. В.И. Чарномского.
по табл. 1.2 (по этой
же таблице, подставляя вместо КнК1;
определяются П1 и П(П1). При необходимости
построения кривой свободной поверхности потока в русле переменной ширины может
быть использован прием проф. В.И. Чарномского.
При этом уравнение Бернулли в приеме Чарномского имеет следующий вид:
|
|
(1.12) |
где hn и vn - глубина и скорость потока во входном сечении, как правило, равны h0 и v0 - нормальной глубине и соответствующей ей скорости при равномерном движении потока;
l - расстояние между двумя сечениями;
![]() и
и ![]() - искомые глубина и
скорость в выходном сечении;
- искомые глубина и
скорость в выходном сечении;
vср, Сср и Rср - средние значения v, С и R между сечениями.
Уравнение Бернулли - Чарномского не применимо для участков перехода потока из бурного состояния в спокойное с образованием прыжка воды.
Кривая свободной поверхности в призматическом русле, кроме таблиц Н.Н. Павловского, может быть построена по графикам приложения 8-11, составленным Ленгипротрансмостом.
РАВНОМЕРНОЕ ДВИЖЕНИЕ ПОТОКА
При равномерном движении потока скорость течения вдоль потока,
расход Q, площадь живого сечения w и его форма остаются
неизменными, а гидравлический уклон ![]()
![]() постоянен и равен геометрическому уклону дна водотока ( i0):
постоянен и равен геометрическому уклону дна водотока ( i0):
iс = i = const.
Равномерное движение имеет место в искусственных водотоках и наиболее часто рассматривается в различных гидравлических расчетах. Элементы равномерного движения участвуют в решениях как общих, так и специальных гидравлических задач.
НЕРАВНОМЕРНОЕ ДВИЖЕНИЕ ПОТОКА
При неравномерном движении потока происходит изменение скорости по его длине. При гидравлических расчетах малых искусственных сооружений, как правило, расход Q по длине сооружения принимается неизменным, т.е. рассматривается установившееся движение. Однако в некоторых случаях при расчетах канав имеет место переменный расход.
Основной характеристикой неравномерного движения является величина удельной энергии Э:
|
|
(1.13) |
Удельная энергия (от гидродинамического напора) измеряется от наинизшей точки дна поперечного сечения.
Глубина потока, при которой удельная энергия сечения для заданного расхода имеет минимальное значение, называется критической глубиной hкр, а состояние потока, в котором h = hкр, называется критическим.
Общее уравнение критического состояния потока для сечения любой формы имеет вид
|
|
(1.14) |
Отсюда критическая глубина для прямоугольного сечения определяется по формуле
|
|
(1.15) |
Для трапецеидального русла
|
|
(1.16) |
Где h kп - критическая глубина для прямоугольного сечения при одинаковой с трапецией ширине дна b;
т - коэффициент заложения откоса, ![]() .
.
Для предварительных расчетов членами ![]() можно пренебречь.
можно пренебречь.
Тогда ![]()
Для треугольного русла
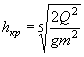
Для круглого сечения h кр находится по графику приложения 28.
В зависимости от соотношения глубин потоков различаются три их состояния (рис. 1.3):
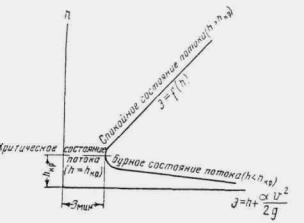
Рис. 1.3. Состояние потока при неравномерном движении
1) бурное состояние потока, при котором глубина меньше критической ( h < hкр );
2) спокойное состояние потока, при котором глубина больше критической ( h > hкр );
3) критическое состояние потока, при котором глубина равна критической ( h = hкр ).
Уклон дна, при котором нормальная глубина потока равна критической, называется критическим уклоном и определяется по формуле
|
|
(1.17) |
Если фактический уклон дна водотока i < iKp, тогда h0 > hкр, и поток, движущийся равномерно, находится в спокойном состоянии. Если же i > iкр, h0< hкр, поток находится в бурном состоянии.
При неравномерном движении независимо от величины уклона поток может находиться как в спокойном (если h > hкр), так и в бурном состоянии (если h < hкр)
При переходе потока из спокойного состояния в бурное происходит явление гидравлического водопада, а при переходе из бурного состояния в спокойное - явление гидравлического прыжка.
Один и тот же расход Q в зависимости от уклона и шероховатости может протекать в данном поперечном сечении русла с различной скоростью и, следовательно, с различной глубиной.
Основные гидравлические понятия и формулы приведены в приложениях 1-3, допускаемые скорости и основные гидравлические коэффициенты - в приложениях 4-7.
ГЛАВА II
РАСЧЕТЫ ТРУБ. БЕЗНАПОРНЫЕ И ПОЛУНАПОРНЫЕ ТРУБЫ
ОБЩИЕ ПОЛОЖЕНИЯ
Отверстия труб, как правило, должны назначаться не менее 1 м, а при длине трубы свыше 20 м - не менее 1,25 м.
На автодорогах II, III, IV и V категорий трубы отверстиями 1 м допускается применять при длине не свыше 30 м, а отверстиями 0,75 м - при длине не свыше 15 м (на съездах допускаются трубы отверстием 0,5 м).
Режим протекания воды через водопропускные трубы под насыпями бывает различным. Обычно трубы стесняют естественные водотоки, в результате чего перед ними образуется некоторый подпор.
Если этот подпор H превышает высоту входного звена трубы hтр не более чем на 20 % ( H £ 1,2 hт p) при обычных оголовках, не более чем на 15 % при раструбных необтекаемых и не более чем на 40 % при обтекаемых ( H £ 1,4 hт p), то поток в трубе имеет свободную поверхность на всем ее протяжении. Такое движение потока называется безнапорным (рис. II.1 и II.2).
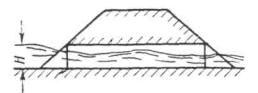
Рис. II .1 Безнапорное движение потока в трубе без повышенного звена
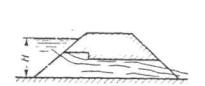
Рис. II .2. Безнапорное движение потока в трубе с повышенным звеном
Когда подпор H при необтекаемых оголовках более чем на 15-20 % превышает высоту входного звена трубы ( H > 1,15 ¸1,2 hтр), труба на входе начинает работать полным сечением, затем возникает перепад, и далее поток снова имеет в трубе свободную поверхность. Такое движение называется полунапорным (рис. II.3).
Если же подпор перед трубой при наличии специальных обтекаемых оголовков превышает более чем на 40 % высоту входного звена трубы ( H > 1,4 hтр) труба начинает работать полным сечением на большей части своей длины, т. е. возникает напорное движение (рис. II.4 и II.5).
Оголовки обычных типов не обеспечивают устойчивость напорного движения в трубе вследствие образования перед входом в трубу воронки, сквозь которую в трубу прорывается воздух, после чего труба начинает работать при полунапорном режиме.
С целью уточнения границ между безнапорным, полунапорным и напорным режимами в Ленинградском политехническом институте был поставлен ряд опытов на круглых трубах с различными оголовками.
В соответствии с Техническими условиями проектирования железнодорожных, автодорожных и городских мостов и труб (СН 200-62) и Строительными нормами и правилами (СНиП П-Д.7-62) трубы, как правило, должны проектироваться по безнапорному режиму и иметь входные и выходные оголовки, обеспечивающие наиболее благоприятное протекание воды и устойчивость насыпи около трубы.
Проектирование водопропускных труб под железные дороги по полунапорному (а при устройстве обтекаемых оголовков также и по напорному) режиму допускается только при пропуске наибольшего расхода водотока (на автомобильных дорогах - при пропуске расчетного расхода) при обязательном применении входных обтекаемых оголовков, обеспечивающих работу труб полным сечением без вакуума, и при наличии фундаментов.
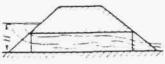
Рис. II .3. Полунапорное движение потока в трубе
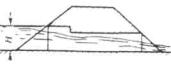
Рис. II .4. Напорное движение потока в трубе с повышенным звеном

Рис. II .5. Напорное движение потока в трубе с обтекаемыми оголовками
Кроме того, в напорных трубах должна быть обеспечена водонепроницаемость стыков звеньев и устойчивость насыпи против воздействия подпора воды и фильтрации. Вообще для пропуска малых водотоков предпочтительнее применение труб, а не мостов, особенно на участках автомобильных дорог с вогнутым профилем. На водотоках, где возможно образование селевых потоков и наледей, применять трубы не рекомендуется.
Наименьшие допустимые возвышения высшей точки внутренней поверхности безнапорных труб Δ h над свободной поверхностью потока при расчетных расходах следует принимать по табл. II. 1.
В соответствии с данными опытов и руководствуясь теми соображениями, что трубы являются узкими хорошо организованными руслами, коэффициент неравномерного распределения скоростей по сечению а принимается для них равным единице.
Как известно, в трубах применялось несколько типов оголовков (рис. II.6): а - портальный; б - коридорный;
в - раструбный; г - воротниковый; д - конический обтекаемый. Каждый из них наряду с положительными качествами имеет существенные недостатки.
Так, например, обтекаемые оголовки трудоемки в изготовлении и значительно уступают по этому признаку портальным оголовкам. С другой стороны, обтекаемые оголовки с точки зрения гидравлики обладают значительными преимуществами перед всеми другими типами, так как увеличивают пропускную способность труб до 40 %. (Труба отверстием 1,25 м с портальным оголовком уступает по пропускной способности трубе отверстием 1 м с обтекаемым оголовком.)
Для круглых труб увеличение пропускной способности обтекаемых оголовков проверялось и подтвердилось ЦНИИСом (схема оголовка на рис. II.7, а) и Союздорнии (схема оголовка на рис. II.7, б).
Ввиду изложенного выше теперь в типовых проектах приняты обтекаемые оголовки.
Таблица II. 1
Наименьшие допустимые возвышения низшей точки внутренней поверхности
безнапорных труб над свободной поверхностью потока
|
Тип отверстия трубы |
Высота отверстия трубы |
|
|
до 3 м |
более 3 м |
|
|
Круглое или овоидальное |
1/4 h тр |
0,75 м |
|
Прямоугольное |
1/6 h тр |
0,50 м |
Рекомендуется считать пропускную способность многоочковых труб равной суммарной пропускной способности одноочковых труб.
Водопропускные трубы следует сооружать только по типовым проектам, поэтому, как правило, гидравлические расчеты труб сводятся к определению подпора перед сооружением и скорости на выходе для отверстий труб, принятых по типовому проекту.
В подавляющем большинстве случаев отверстия труб должны рассчитываться с учетом аккумуляции; Ниже приводится упрощенный расчет, разработанный Харгипротрансом для круглых и прямоугольных труб по действующим типовым проектам № 101 и 180.
Отверстия труб по этим проектам рассчитаны в соответствии с Руководством по гидравлическим расчетам малых искусственных сооружений и русел (Трансжелдориздат, 1961 г.), а также с учетом работ Ленинградского Политехнического института.
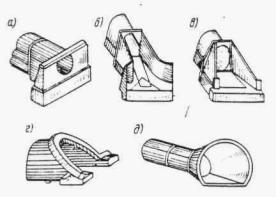
Рис. II .6. Типы оголовков
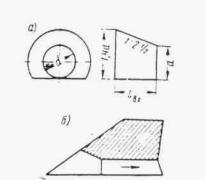
Рис. II .7. Схемы обтекаемых оголовков
При необходимости в процессе эксплуатации увеличить отверстия существующих труб с необтекаемыми оголовками в ряде случаев удавалось ограничиться заменой существующих оголовков обтекаемыми или (в прямоугольных, трубах) заменой обычного входного звена повышенным, без увеличения отверстия..
При незначительной аккумуляции водопропускная способность существующих труб с необтекаемыми оголовками может быть увеличена путем устройства обтекаемых открылков по предложению канд. техн. наук Л.Г. Рабухина (Волгоградский институт городского хозяйства).
При затопленном входе и незатопленном выходе водопропускные трубы с необтекаемыми (портальными, раструбными) оголовками не работают полным сечением. Следовательно, недоиспользуется площадь их поперечного сечения даже при пропуске максимальных расходов и при больших напорах Н.
Необтекаемые оголовки вызывают сжатие потока в вертикальной плоскости при обтекании верхнего ребра входного отверстия, поэтому для создания напорного режима особенно важна форма верхней части входного оголовка трубы.
Плавный вход воды в трубу обеспечивается при устройстве над входным отверстием обтекаемого открылка в виде козырька, очерченного по дуге круга радиусом 1,7 d (рис. II .8 и II.9).
Обтекаемый открылок легко осуществить в натуре в виде железобетонной плиты, опирающейся на две стойки и портальную стенку трубы. Открылки имеют простую форму, небольшие размеры и особенно целесообразны при реконструкции труб с недостаточной пропускной способностью, так как позволяют повысить их пропускную способность без капитального переустройства.
Поскольку труба может работать напорным режимом, следует проверить надежность изоляции в стыках ее звеньев.
При наличии обтекаемого открылка труба работает полным сечением по всей длине при Н > 1,2 d ( d - диаметр трубы). При напорах 1,5 ¸ 2 d пропускная способность трубы с обтекаемым открылком повышается на 30-35 %.
На основании экспериментальных данных построен график зависимости пропускной способности Q от напора Н для труб с обтекаемым открылком и с обычными оголовками (рис. II.10). Из указанного графика видно, что по пропускной способности труба диаметром 1 м с обтекаемым открылком эквивалентна трубе d = 1,25 м с необтекаемыми оголовками и т. д.
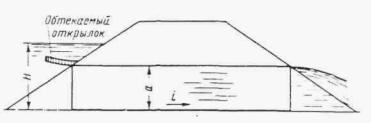
Рис. II .8. Трубы с обтекаемым открылком (козырьком)
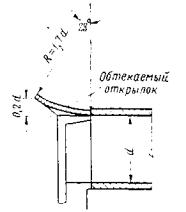
Рис. II .9. Схемы обтекаемого открылка
В действующих типовых проектах приняты: в прямоугольных трубах отверстиями 1-2,5 м раструбные оголовки с повышенным звеном на входе; для. труб отверстиями 3 и 4 м - те же оголовки, но с нормальным входным звеном; в круглых трубах для автомобильных дорог портальные оголовки для отверстий 0,5 и 0,75 м и раструбные с коническими входными и выходными звеньями для отверстий 1-2 м (для отверстия 1 м предусмотрен также оголовок с нормальным входным звеном для применения на водотоках с расходами до 1,6 м3/сек).
В трубах под железные дороги для всех отверстий (1; 1,25; 1,5 и 2 м) предусмотрены раструбные оголовки с коническими входными и выходными звеньями.
Типовые трубы запроектированы для безнапорного и полунапорного режимов протекания воды.
Безнапорный режим принят для расчетных расходов, пропускаемых с обеспечением требуемых таблицей II.1 зазоров между наивысшей точкой внутренней поверхности трубы и уровнем воды на протяжении всей трубы. Наибольший расход пропускается частично по безнапорному режиму и частично по полунапорному.
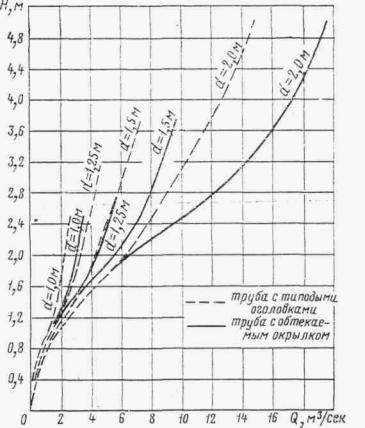
Рис. II .10. Пропускная способность труб с типовыми оголовками и. с обтекаемыми открылками
Таблица II.2
Критические уклоны в трубах (ориентировочно)
|
Отверстия в м |
Трубы |
|
|
круглые |
прямоугольные |
|
|
1-1,25 |
0,007 |
0,009 |
|
1,5-2 |
0,006 |
0,008 |
|
3 |
- |
0,007 |
|
4 |
- |
0,006 |
Наибольшие допускаемые расходы в трубах приняты из условия, чтобы скорость воды на выходе не превышала допускаемой (при принятом типе укрепления) больше чем на 35 %. При этом независимо от высоты насыпи и типа укрепления глубина подпертой воды перед трубой не должна превышать 4 м.
В приложениях 15 и 16 приведены гидравлические характеристики для труб по типовым проектам (при уклонах в трубах, равных критическим).
УПРОЩЕННЫЙ РАСЧЕТ ОТВЕРСТИЙ ТРУБ С УЧЕТОМ АККУМУЛЯЦИИ
Расчет заключается в нахождении точек пересечения графиков пропускной способности сооружений с графиком зависимости наибольшего расхода в сооружении Q cоо p от подпертой глубины воды перед сооружением H.
По полученным в точках пересечения значениям Q coop и Н в зависимости от допускаемой подпертой глубины, сообразуясь с технико-экономическими показателями, выбирается род трубы и размер отверстия.
Зависимости Q coop = f ( H3) выражаются отрезками прямых линий и строятся в отдельности для расчетного и наибольшего расходов по выражению
|
|
( II.1) |
Координаты точек для построения этих линий соответствующей вероятности определяются по соотношениям:
H3 = 0, Q cоо p = Qмакс
![]() , Q cоо p = 0
, Q cоо p = 0
Здесь Qмакс и W - соответственно расход принятой вероятности превышения в м3/сек и объем стока для гидрографа с наибольшим расходом в тыс. м3;
![]() -
соответственно уклон лога и склонов перед сооружением в %0;
-
соответственно уклон лога и склонов перед сооружением в %0;
k0 - коэффициент, определяемый по табл. II.3 в зависимости от очертания пруда перед сооружением в плане и от продольного профиля по логу.
Таблица II.3
Значение коэффициента k0
|
Очертание пруда в плане |
Продольный профиль лога перед сооружением |
Профиль берегов |
||
|
выпуклый |
прямолинейный |
вогнутый |
||
|
С вогнутыми параболами |
Выпуклый |
133 |
152 |
191,5 |
|
Прямолинейный |
152 |
200 |
229 |
|
|
Вогнутый |
191,5 |
229 |
271 |
|
|
Прямолинейный треугольник |
Выпуклый |
152 |
200 |
229 |
|
Прямолинейный |
200 |
235 |
264 |
|
|
Вогнутый |
229 |
264 |
321 |
|
|
С выпуклыми параболами |
Выпуклый |
191,5 |
229 |
271 |
|
Прямолинейный |
229 |
264 |
321 |
|
|
Вогнутый |
271 |
321 |
378 |
|
ПРИМЕР РАСЧЕТА ОТВЕРСТИЙ ТРУБ С УЧЕТОМ АККУМУЛЯЦИИ
(рис. 11.11-11.13)
Исходные и вычисленные данные для расчета помещены в ведомости на стр. 19 (пример и графики составлены Харгипротрансом).
Для построения зависимости Q coop = f ( H3), выраженной прямой, откладываем:
для вероятности 1/300 по вертикальной оси ![]() на рис II.13 сплошная линия I);
на рис II.13 сплошная линия I);
по горизонтальной оси Q300 = 26,3 м3/сек;
для вероятности 1/100 соответственно H3 = 105, Q100= 14,2 м3/сек (на рис. II.13 сплошная линия II).
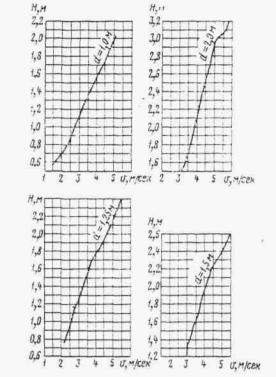
Рис. II .11. Кривые скоростей на выходе (в круглых трубах) в зависимости от глубины подпора H
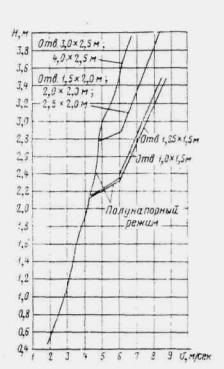
Рис. II .12. Кривые скоростей v на выходе (в прямоугольных трубах) в зависимости от глубины подпора H
Прямая, соединяющая соответствующие точки H3 и Q, пересекает кривые пропускной способности труб. Координаты точек пересечения дают: по оси H - подпор перед сооружением, по оси Q - расчетный расход, пропускаемый сооружением с учетом аккумуляции.
Выбор отверстия трубы производится по технико-экономическим соображениям с учетом допускаемого подпора.
Для прямоугольной трубы отверстием 2×2 м Qcoop (расч) = 12,3 м3/сек; H = 2,45 м- Qcoop макс = 18,15 м3/сек, H = 3,38 м.
Для принятого отверстия трубы, пользуясь графиком рис. II.12, определяем по установленному подпору H = 2,45 м, скорость на выходе vвых = 4,6 м/сек.
В тех случаях, когда по графику рис. II.13 необходимо получить зависимость = f( H) без учета аккумуляции, следует пользоваться шкалой H вместо шкалы H3 .
Подробные графики для расчетов прямоугольных и круглых труб с учетом аккумуляции, составленные Киевгипротрансом (инж. Ф. С. Титовым), приведены в приложениях 18-24.
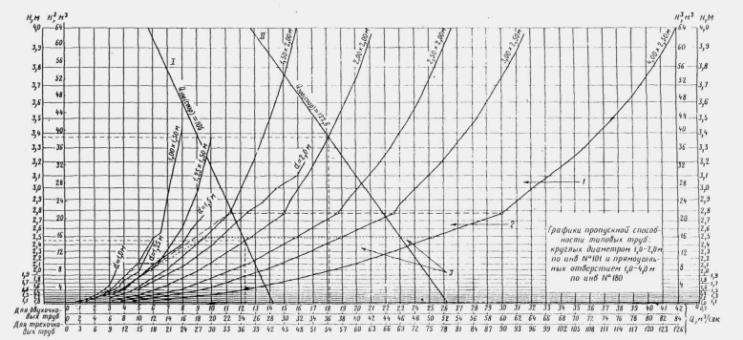
Рис. II .13. 1-полунапорный режим; 2 -переходный режим; 3 -безнапорный режим (для прямоугольных труб)
Таблица II.4.
Объект ............
Расчет отверстия малых искусственных сооружений с учетом аккумуляции
по ВСН 63-81 (упрощенный способ)
|
№ п/п |
Километр или участок |
Пикет или плюс |
Ливневой сток |
Уклоны в ‰ |
K 0 |
|
|
|
||||
|
Q 100 в м3/сек |
W 100 в тыс. м3 |
Q 300 в м3/сек |
W 300 в тыс. м3 |
I л |
I c |
|||||||
|
1 |
1 |
54+00 |
15 |
75 |
26,3 |
87,5 |
17 |
23 |
280 |
1,4 |
105 |
122,6 |
Таблица II.5
|
Род сооружения |
Отверстие в м |
По графикам |
Принятые расходы с учетом аккумуляции не должны быть меньше |
||||||||
|
Расчетный расход |
Максимальный расход |
||||||||||
|
Расчетный расход |
Максимальный расход |
||||||||||
|
Q соор в м3/сек |
H в м |
v в м/сек |
Q соор в м3/сек |
H в м |
0,33 Q 100 ливневой в м3/сек |
Q 100 снеговой в м3/сек |
0,33 Q 300 ливневой в м3/сек |
Q 300 снеговой в м3/сек |
|||
|
Прямоугольная железобетонная труба |
2×2 |
12,7 |
2,52 |
4,6 |
18,3 |
3,37 |
5,0 |
9,8 |
8,7 |
16,4 |
|
ПРОЧИЕ СЛУЧАИ РАСЧЕТА ТРУБ
В тех случаях, когда отверстия труб должны рассчитываться без учета-аккумуляции, а также когда трубы проектируются с уклонами, значительно отличающимися от критических, при безнапорных трубах с затопленным сжатым сечением и при затопленном входном отверстии расчеты производятся в следующем порядке.
При данном расходе Q и принятом в первом приближении отверстии В (для прямоугольных труб) для безнапорного режима определяется критическая глубина по формуле (1.15)
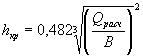 ;
;
для круглых труб hк p определяется из уравнения (1.14)
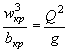
и по графику приложения 28.
Подпор перед трубой определяется по формуле
|
|
( II.2) |
Глубина в сжатом сечении для прямоугольных труб
![]() =(0,90 ¸0,85)
=(0,90 ¸0,85) ![]() ,
,
где 0,90 принимается при Q = 1,5 ¸ 3,5 м3/сек
0,85 принимается при Q = 4 ¸ 8,6 м3/сек.
Для круглых труб hсж = 0,91 hкр.
Скорость на выходе
![]()
Критический уклон по ф-ле (1.17)
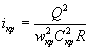
Для круглых труб (типовой проект № 101) скорость на выходе при i факт iк p определяется по формуле
![]()
При iфакт > iкр по формуле
![]()
Следует отметить, что, как правило, трубам придаются не
критические уклоны (при которых в типовых проектах определены гидравлические
характеристики), а уклоны, равные уклонам местности. Это не отражается на
пропускной способности труб, но влияет в первую очередь на скорость на выходе ![]() .
.
Эта скорость может быть откорректирована по уклону iфакт (фактический
уклон трубы), когда имеется скорость ![]() определенная для
типовой трубы с уклоном iкр:
определенная для
типовой трубы с уклоном iкр:
|
|
( II.3) |
При полунапорном режиме подпор перед прямоугольной трубой определяется по формуле
|
|
( II.4) |
где hсж = e h hBх; zh e h = 0,643; e w = 0,636; j= 0,972.
Скорость на выходе
|
|
( II.5) |
Для типовых круглых труб с раструбными оголовками при
соотношении ![]() безнапорный режим
переходит в напорный.
безнапорный режим
переходит в напорный.
При напорном режиме подпор определяется по формуле
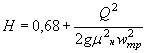
где ![]() = 0,87 при длине трубы до 20 м;
= 0,87 при длине трубы до 20 м;
при Lтр>20 м
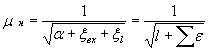
![]() (здесь l = Lтр - 20)
(здесь l = Lтр - 20)
Скорость на выходе
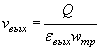
где ![]() = 0,91 - для меньшего
диаметра конического звена
= 0,91 - для меньшего
диаметра конического звена
![]() = 0,64 - для большего диаметра конического звена.
= 0,64 - для большего диаметра конического звена.
Для определения подпора разрешается также пользоваться табл. II.6, где Н' - глубина воды у портала входного оголовка.
Таблица II .6
Соотношение между hкр в трубе, H0 и Н' (см. рис. 11.14)
|
Тип входного оголовка |
Подпор H0 |
Н' |
|
Обтекаемый |
1,6 hкр |
1,4 hкр |
|
Раструбный |
1,8 hкр |
1,6 hкр |
|
Портальный |
1,9 hкр |
1,7 hкр |

Рис. 11.14. Соотношение между h кр H 0 и Н' (в трубе)
Далее определяется подходная скорость по формуле
![]() ,
,
где w0 - площадь живого сечения естественного русла перед трубой при глубине Н0.
Уточняется значение Н с учетом подходной скорости v0 по формуле
|
|
( II.6) |
Практически при паводочных расходах v0 » 0.
Расчеты рекомендуется вести в табличной форме (табл. II.7).
Таблица II.7
Расчет труб по безнапорному режиму при Q pacч, а также проверка при Qмакс (графы 16-20)
|
|
|
|
|
или |
wсж = h сж b сж |
|
v сж = vвых ,< vдоп vдоп при h сж |
Или по табл. II .6 |
w 0 = Hb 0 ( b 0- ширина естеств. русла) |
|
1 |
2 |
3 |
4 |
о |
6 |
7 |
8 |
9 |
10 |
|
|
|
|
|
|
|
|
|
|
|
Продолжение
|
|
l вх =(1,5 ¸ 1,6) H 0 |
|
(или по приложениям 6 и 7) |
|
|
|
|
|
|
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
|
|
|
|
|
|
|
|
|
|
Производится расчет в первом приближении по принятой величине b при необходимости увеличения отверстия (если не соблюдены неравенства в графах 8, 11 пли 20) расчеты повторяются при новом значении b.
По данным ЦНИИСа, границы между безнапорным и полунапорным режимами при обычных оголовках и между безнапорным и напорным режимами при обтекаемых оголовках характеризуются величинами, приведенными в табл. II.8
Таблица II.8
Величины Н, Q и hсж (по ЦНИИСу) в случае, когда уклон дна в безнапорных трубах больше уклона трения
|
Расчетные величины |
Прямоугольные трубы |
Круглые трубы |
||
|
Необтекаемые оголовки |
Обтекаемые оголовки |
Необтекаемые оголовки |
Обтекаемые оголовки |
|
|
Глубина перед входом (подпор Н ) |
1,2 h тр |
1.4 h тр |
1,2 d |
1,4 d |
|
Расход Q |
|
|
l ,52 d5/2 |
2,17 d 5/2 |
|
Глубина в сжатом сечении h сж. |
0,62 h тр |
0.95 h тр |
0,63 d |
0,95 d |
РАСЧЕТ БЕЗНАПОРНЫХ ТРУБ ПРИ ЗАТОПЛЕННОМ СЖАТОМ СЕЧЕНИИ
В трубах на зарегулированных каналах, расположенных на участке подпора, образуемого плотиной или другим водотоком, течение воды становится несвободным и сжатое сечение затопленным.
Условия.затопления определяются соотношением
hбыт ³ 1 ,25 hкр
Схема протекания воды в этих условиях показана на рис. II.15.
При несвободном истечении из трубы неравномерное движение
потока будет иметь место только при 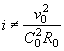 , где v0,
C0 и
R0 определяются
по выходному сечению, в котором устанавливается глубина hбыт.
, где v0,
C0 и
R0 определяются
по выходному сечению, в котором устанавливается глубина hбыт.
Целесообразно трубы с затопленным выходным отверстием укладывать с уклоном, при котором нормальная глубина в трубе h0 равна бытовой глубине ( h0 = hбыт). В этом случае движение потока в трубе будет равномерным, с постоянной глубиной hбыт.
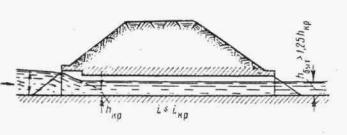
Рис II .15. Схема протекания потока в трубе при затопленном сжатом сечении
Таким образом, при затоплении сжатого сечения могут рассчитываться сооружения, для которых известно отверстие b и высота в свету hтр. расчеты ведутся в следующем порядке.
1. По формуле (1.15) или по приложению 28 определяют hкр.
2. Проверяют отношение ![]()
3. Определяют wвых при
глубине воды в трубе ![]()
4. Определяют скорость на выходе из трубы при глубине ![]()
5. Определяют вспомогательные гидравлические величины для выходного
сечения при глубине ![]() , смоченный периметр χвых гидравлический
радиус
, смоченный периметр χвых гидравлический
радиус ![]()
6. Производят построение кривой свободной поверхности потока в трубе от выходного отверстия к входному по уравнению Бернулли - Чарномского, имеющего вид
![]()
Где
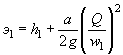
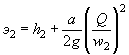
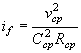
За известное принимается h (глубина
в следующем за выходным сечении), причем она должна отличаться от ![]() не более чем на 5-10 см.
не более чем на 5-10 см.
Задаваясь последовательно значениями h1, h2, h3 и т. д., строят кривую свободной поверхности потока в трубе до сечения, отстоящего на 3-5 м от входного отверстия.
Далее задача решается подбором величин h и v.
7. По полученному hвх определяют wвх и скорость течения на выходе
![]()
8. Определяют подпор перед трубой из выражения
![]()
Далее определяют величину подходной скорости v0 и уточняют значение подпора по формуле ( II.6).
РАСЧЕТ БЕЗНАПОРНЫХ ТРУБ ПРИ УКЛОНЕ, МЕНЬШЕМ КРИТИЧЕСКОГО
При уклоне в трубе, меньшем критического, устанавливается следующая картина протекания воды при безнапорном режиме.
Свободная поверхность воды образует выпуклую кривую спада (рис. 11.16). В конце трубы (на некотором расстоянии от ее выходного отверстия) образуется критическая глубина.
При достаточно длинных трубах сжатое сечение на входе в трубу не образуется, и вода спокойно сливается в трубу. Этот случай, как наиболее часто наблюдающийся на практике, принимается для расчета.
Наибольший расход воды, который может пропустить труба при безнапорном режиме, определяется условием соблюдения норм по степени заполнения трубы у входного отверстия, где устанавливается наибольшая глубина.
Задачи, которые приходится решать для труб, уложенных с уклоном i < i Kp, могут быть двух типов:
1) при заданном расходе Q, уклоне трубы i и длине трубы L требуется подобрать ее поперечное сечение (отверстие и высоту);
2) по заданному поперечному сечению трубы (отверстию b и hтр), длине L и уклону i требуется определить наибольший возможный расход Q.
Первая задача может быть решена методом последовательного подбора отверстия b, а вторая - методом последовательного подбора расхода Q. Для этого строят кривую свободной поверхности в трубе по направлению от низового отверстия к верховому.
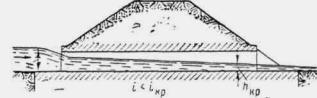
Рис. II .16. Кривая спада при уклоне трубы, меньшем критического
Решение обеих задач выполняется при помощи уравнения Бернулли - Чарномского (1.12).
Если требуется подобрать наибольший допустимый расход Q для трубы отверстием b, то расчеты ведутся исходя из следующих положений.
Глубина на входе hвх меньше h0 и больше hкр:
h0 > hвх > hкр
При достаточно длинной трубе hвх » h0, а так как можно считать hвх = 3/4 hтр, то h0 » 3/4 hтр
По известному h 0 легко найти Q по формуле
![]() (при
прямоугольном сечении).
(при
прямоугольном сечении).
Для труб круглого сечения расход можно определять по табл. II.9.
Таблица II.9
Расходные и скоростные характеристики круглых труб
|
Степень наполнения круглых труб |
Расходные характеристики, характеристики скорости и критические функции |
Степень наполнения круглых труб |
Расходные характеристики, характеристики скорости и критические функции |
||||
|
Критическая функция |
Отношение расходных характеристик |
Отношение скоростных характеристик |
Критическая функция |
Отношение расходных характеристик |
Отношение скоростных характеристик |
||
|
|
|
|
|
|
|
|
|
|
0,20 |
0,001 |
0,080 |
0,565 |
0,65 |
0,166 |
0,766 |
1,113 |
|
0,25 |
0,005 |
0,129 |
0,661 |
0,70 |
0,220 |
0,850 |
1,137 |
|
0,30 |
0,009 |
0,188 |
0,748 |
0,75 |
0,294 |
0,927 |
1,152 |
|
0,35 |
0,016 |
0,256 |
0,821 |
0,80 |
0,382 |
0,994 |
1,159 |
|
0,40 |
0,025 |
0,332 |
0,889 |
0,85 |
0,500 |
1,048 |
1,157 |
|
0,45 |
0,040 |
0,414 |
0,948 |
0,90 |
0,685 |
1,082 |
1,142 |
|
0,50 |
0,060 |
0,500 |
1,000 |
0,95 |
1,035 |
1,087 |
1,108 |
|
0,55 |
0,088 |
0,589 |
1,045 |
|
|
|
|
|
0,60 |
0,121 |
0,678 |
1,083 |
|
|
|
|
Подпор перед трубой определяется из выражения
![]()
Далее определяют величину подходной скорости v0 и уточняют значение подпора по формуле ( II.6).
РАСЧЕТ БЕЗНАПОРНЫХ ТРУБ ПРИ УКЛОНЕ, БОЛЬШЕМ КРИТИЧЕСКОГО
Согласно исследованиям М. И. Виноградова (МИИТ) и других при уклоне, большем критического, в безнапорных трубах устанавливается следующая картина протекания воды:
1) в случае когда i = iсж (где  ) в трубе устанавливается равномерное движение с постоянной
глубиной hсж (рис. II.17);
) в трубе устанавливается равномерное движение с постоянной
глубиной hсж (рис. II.17);
2) в случае когда iкр < i < iсж, на входе в трубу образуется сжатая глубина и выпуклая кривая подпора с глубиной h £ h0 на выходе (рис. II.18), причем h0 > hсж;
3) в случае когда i > iсж, образуется вогнутая кривая спада (рис. II.19).
Для круглых труб легко определить hкр или h0, пользуясь табл. II.9. В этой таблице K0 и Kd - расходные характеристики сечения:
K0 - при нормальной глубине потока h0 < d,
|
|
( II.7) |
K d -для целиком заполненного сечения при h0 = d,
|
K d = 24d8/3 |
(II.8) |
w0 и wd - соответственно скоростные характеристики сечения при h0 < d и h0 = d,
|
|
(II.9) |
|
wd = 30,5d2/3 |
( II.10) |
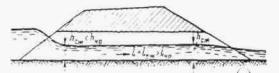
Рис. II .17. Равномерное движение потока
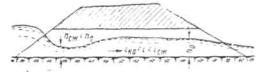
Рис. II .18. Выпуклая кривая подпора
Пользование этой таблицей поясняется примером.
Пример. Определить глубины на выходе при Q = 1,6 м3/сек, d = 1,25 м и уклонах i1 = 0 и i2 = 0,01.
Решение. 1. При уклоне i1 = 0 на выходе должна установиться критическая глубина hкр
Критическая функция равна
![]()
по табл. II.9
этому значению отвечает ![]() = 0,55
и глубина на выходе hкр = 0,55·1,25 = 0,69 м.
= 0,55
и глубина на выходе hкр = 0,55·1,25 = 0,69 м.
Рис. II .19. Вогнутая кривая спада
2. При уклоне i2 = 0,01, который больше iкр, на выходе должна устанавливаться нормальная глубина равномерного движения h0 < hкр.
Для определения этой глубины вычисляем расходную характеристику всего сечения
Kd =24 d8/3 = 24·1,258/3 =43,2 м3/сек
и необходимую расходную характеристику
![]() м3/сек
м3/сек
![]()
По табл II.9
находим ![]() = 0,42;
следовательно, h0 = 0,42·1,25 = 0,52 м,
т. е.
= 0,42;
следовательно, h0 = 0,42·1,25 = 0,52 м,
т. е.
действительно h0 < hкр.
По той же табл. II.9 находим
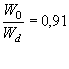
Wd = 30,5 d2/3 = 30,5·1,252/3 = 35,5 м/сек
W0 = 0,91 Wd = 0,91·35,5 = 32 м/сек;
v0 = W0 ![]() = 32
= 32 ![]() = 3,2 м/сек.
= 3,2 м/сек.
В круглых полунапорных трубах скорость на выходе также целесообразно определять по табл. II.9 (см. пример).
Пример. Принимаем данные предыдущего примера Q = 1,6 м3/сек i2 = 0,01, но вместо трубы d= 1,25 м принимаем d = 1 м. Определяем
![]() м3/сек
м3/сек
Kd =24 d8/3 = 24·1=24 м3/сек
![]()
По табл II.9 находим
![]() ; h0 = 0,60 м,
; h0 = 0,60 м,
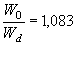
Wd = 32,5 d2/3 = 32,5 м/сек
W0 = 1,083·32,5 = 33 м/сек;
v0 = W0 ![]() = 33
= 33 ![]() = 3,3 м/сек.
= 3,3 м/сек.
В трубах с уклоном i > i Kp гидравлические сопротивления на некоторой длине трубы не уравновешиваются силами тяжести и поэтому на этой длине скорость течения продолжает нарастать до тех пор, пока не установится равновесие.
На остальной длине трубы скорость течения становится постоянной ( v0), отвечающей равномерному режиму движения.
Задачи, которые приходится решать для труб, уложенных с уклоном i, большим критического, могут быть трех типов:
1) по заданным расходу Q, уклону i и длине трубы L подобрать поперечное сечение трубы;
2) по заданным поперечному сечению трубы ( отверстию b) длине L и уклону i определить наибольший возможный расход Q и скорость течения на выходе vвых;
3) по заданным скорости на выходе vвых, уклону i, длине L и отверстию b определить расход Q.
Возможны различные сочетания этих задач. Прямым путем, т. е. последовательным построением кривой свободной поверхности в направлении от верхового отверстия трубы к низовому, решается задача второго типа. Две другие задачи (1 и 3) решаются методом последовательного подбора.
Для решения второй задачи прежде всего задаются допустимой глубиной во входном сечении hвх, которая будет в то же время сжатой глубиной hсж. и вычисляют соответственно площадь поперечного, сечения wвх = wсж и ширину свободной поверхности Ввх = Всж.
При данном hкр по уравнению ( II.14) определяется расход
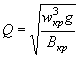
Скорость течения во входном сечении будет
![]()
Определяются гидравлические характеристики входного сечения
w сж, χ сж R сж c сж
Далее ведется построение свободной поверхности по уравнению ( I.11).
В результате последовательных решений уравнения ( I.11) получается глубина в конце кривой спада wвых, площадь живого сечения wвых и отсюда скорость
![]()
В большинстве случаев длина трубы бывает больше длины кривой спада, так что на выходе образуется нормальная соответствующая данному расходу и форме сечения трубы глубина h0.
РАСЧЕТ ТРУБ С ЗАТОПЛЕННЫМ ВХОДНЫМ ОТВЕРСТИЕМ (ПОЛУНАПОРНЫХ)
Движение в трубе при затопленном входном отверстии и при свободной поверхности потока на всем остальном протяжении трубы называется полунапорным и характеризуется тем, что гидростатическое давление в трубе аналогично давлению при безнапорном режиме (рис. 11.20). Поэтому трубы с затопленным входным отверстием могут конструктивно решаться, как и безнапорные, т. е. без специальных мероприятий, предусматриваемых для напорных труб.
Полунапорный режим может образоваться в трубах с обычными (необтекаемыми) оголовками и сохраняться в некотором диапазоне расходов. При дальнейшем увеличении расхода воды полунапорное движение может перейти в напорное, когда труба на части своей длины (иногда почти по всей длине) работает полным сечением (рис. II.21).

Рис. II.20. Полунапорное движение потока
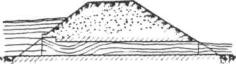
Рис. II .21. Напорное движение потока
Необходимой предпосылкой образования и поддержания в трубе полунапорного режима является условие, чтобы уклон трубы был более уклона трения ( i > if), который определяется по формуле
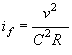
где v - скорость течения воды в трубе, работающей полным сечением.
При расчете труб по полунапорному режиму принимают, что:
а) труба имеет критический по расчетному расходу уклон iкр (или немного больший, чем iкр);
б) нижний бьеф не оказывает влияния на протекание воды в трубе.
Расчет ведется в следующем порядке.
В первом приближении задаются отверстием трубы b и при заданном расходе Q paсч ее рассчитывают как безнапорную.
Затем выясняется образование полунапорного режима и если Н < l,2 h Tp, то трубу рассчитывают вновь как полунапорную.
Для круглых труб полунапорный режим имеет место при ![]() >1,52 (обычные оголовки), где d - диаметр
трубы.
>1,52 (обычные оголовки), где d - диаметр
трубы.
Расчетное уравнение для полунапорного режима имеет вид
|
|
( II.11) |
w сж = e w тр
h сж = e h тр
где h тр - высота отверстия входного звена трубы.
Значения расчетных коэффициентов на входе при полунапорном режиме приведены в табл. 2 приложения 12.
Задачи, решаемые при полу напорном режиме, бывают двух типов:
1) по данному расходу Q и отверстию трубы b определить подпор перед трубой H и скорость течения на выходе vвых;
2) по данной высоте насыпи Ннас и отверстию трубы b определить предельно допустимый для трубы расход Q и скорость течения на выходе vвы x.
Для решения первой задачи уравнение ( II.11) преобразуется в следующий вид:
|
|
( II.12) |
При повышенном входном звене в формулу (П.12) следует подставлять вместо hтр высоту входного звена hвх, т. е.
h сж = e h вх и w вх = bh вх
где
h сж = eвх h тр
Скорость течения на выходе приравнивается к скорости течения в сжатом сечении и определяется по формуле
|
|
( II.13) |
Для решения второй задачи в уравнении ( II.12) значение подпора Н заменяется величиной предельно допустимого подтопления бровки земляного полотна
![]()
где ![]() - допускаемое техническими условиями возвышение бровки над
подпертым уровнем. Тогда уравнение ( II.11) принимает следующий вид:
- допускаемое техническими условиями возвышение бровки над
подпертым уровнем. Тогда уравнение ( II.11) принимает следующий вид:
|
|
( II.14) |
Скорость на выходе определяется по формуле
![]()
НАПОРНЫЕ ТРУБЫ
Общие положения
Специальные требования, предъявляемые к напорным водопропускным трубам под железными и автомобильными дорогами, указаны выше.
Несмотря на эти требования, безусловно усложняющие конструкцию напорных труб и насыпей около них, применение таких труб может дать экономический эффект, так как пропускаемый ими расход воды в некоторых случаях может в несколько раз превышать расход при безнапорном режиме.
Однако для эффективного применения напорных труб должны иметь место следующие благоприятные условия:
а) бассейн должен иметь преимущественно ливневой сток, дающий более кратковременные паводки, чем снеговой (при расчете на Qснег режим должен быть безнапорным);
б) паводочный поток не должен нести большого количества наносов;
в) труба должна быть гарантирована от образования в ней наледей;
г) насыпь должна иметь достаточную высоту, соответствующую подпору при Qмакс
д) грунты русла должны быть достаточно устойчивы против размыва с тем, чтобы не приходилось предусматривать значительных мероприятий по гашению высоких скоростей на выходе из трубы;
е) уклон трубы должен быть меньше уклона трения i < if.
Рекомендуется не назначать напорных труб отверстием более 1,5 м, так как при больших отверстиях значительные массы воды на выходе из трубы будут иметь большую разрушительную силу и для гашения энергии придется предусматривать дорогостоящие мероприятия.
Как правило, напорные трубы проектируют круглыми с обтекаемыми входными оголовками, при которых вакуум и полунапорный режим не образуются: с увеличением расхода Q безнапорный режим прямо переходит в напорный.
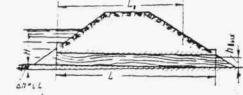
Рис. II .22. Напорный режим в трубе при незатопленном выходном отверстии

Рис. II .23. Напорный режим в трубе при затопленном выходном отверстии
Для устранения, возможности фильтрации воды через насыпь вдоль трубы нужно предусматривать водонепроницаемые экраны по откосу насыпи (у входного оголовка) и внутри насыпи, а также устройство специальных водонепроницаемых швов между звеньями.
Следует различать два случая напорного режима в трубах: при незатопленном выходном отверстии (рис. II.22) и при затопленном (рис. II.23).
О бщий метод расчета
Методика расчета напорных труб построена на аналогии работы трубы и внешнего насадка (рис. II.24), через который происходит истечение воды в атмосферу.
Длинные напорные трубы оказываются малоэффективными, так как с увеличением длины трубы коэффициент j уменьшается.
Наибольшая высота насыпи (на однопутных участках), при которой круглые трубы достигают оптимальной длины ( L = 55 d) приведена в табл. II.10.
В трубах длиной от L » 5 d до L £ 55 d коэффициент скорости изменяется в пределах от 0,82 до 0,62; промежуточные значения можно принимать по линейной интерполяции согласно графику рис. II.25.
Практически для получения надежного напорного режима, не нарушаемого кавитацией, предельным допускаемым подпором перед напорной трубой следует считать Н = 10 м.
Использование такого подпора (10 м) требует особых мероприятий по предохранению земляного полотна от фильтрации и нижнего бьефа от размыва.
Расчет напорной трубы, не испытывающей влияния нижнего бьефа, рекомендуется выполнять в следующем порядке.
1. По заданному Qмакс подбирается отверстие (диаметр) трубы d. При этом подборе можно пользоваться ориентировочными значениями возможных (допустимых) наибольших расходов в круглых (напорных) трубах, приведенными в табл. П. 10.
Таблица II.10
Оптимальная высота однопутных насыпей для круглых напорных труб и максимальный
расход, пропускаемый этими трубами
|
Отверстие трубы в м |
Высота насыпи в м |
Максимальный расход в м3/сек |
|
1,00 |
16,0 |
6 |
|
1,25 |
20,0 |
10 |
|
1,50 |
25,0 |
15 |
2. Определяется скорость течения на выходе из трубы по формуле
![]()
где ![]() - площадь живого сечения в выходном
отверстии трубы.
- площадь живого сечения в выходном
отверстии трубы.
Высота двухпутных насыпей принимается на 2 м менее указанной в табл. II.10.
При определении wвых с целью упрощения расчетов принимается допустимая схематизация, согласно которой в выходном сечении глубина потока Нвых = 0,75 hкр; глубина hкр устанавливается в потоке на расстоянии hкр от выходного сечения (рис. II.26). Уравнение неравномерного движения потока рекомендуется применять только начиная с сечения, отстоящего на 2 hкр от выходного сечения, где глубина достигнет 1,25 hкр
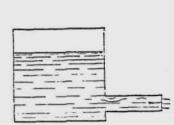
Рис. II .24. Схема работы внешнего насадка
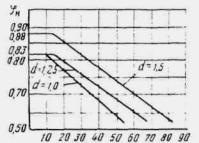
Рис. II .25. График величин коэффициентов скорости
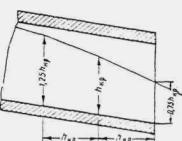
Рис. II .26. Схема потока в выходном отверстии
3. По найденному значению vвых проверяется соответствие принятого укрепления в нижнем бьефе трубы.
4. Определяется подпор перед сооружением, обусловливаемый скоростью течения, по формуле
|
|
( II.15) |
где eвых = 0,75;
![]() -
коэффициент сопротивления по длине,
-
коэффициент сопротивления по длине,
![]()
l0 - длина участка трубы, работающего полным сечением.
Для круглой трубы
![]()
![]() - коэффициент
сопротивления на входе,
- коэффициент
сопротивления на входе,
![]() = 0,505 + 0,303 sin q + 0,226 sin2 q
= 0,505 + 0,303 sin q + 0,226 sin2 q
(рис . II.27).
В формулу ( II.15) с достаточной для целей практики точностью может вводиться значение l0 (длина, на которой труба работает полным сечением): l0 = 0,8 L, где L - полная длина трубы (рис. II.28).
Длина трубы L на однопутных участках может приниматься по формулам ( II.16) и ( II.17) (см. рис. II.28):
при высоте насыпи Hнас<6 м
|
L = 3HHac + B - (a+b), |
( II.16) |
где ( a+ b)- сумма длин входного и выходного оголовков с их конусами;
при высоте насыпи Hнас > 6 до 12 м
|
L - 18,0 + В + 3,5( Hнас - 6) - ( a- b). |
( II.17) |
Если полученный подпор H >( Hнас - 0,5), т. е. не удовлетворяет условиям в отношении подтопления бровки земляного полотна, то или принимается решение о подъемке бровки, или отверстие трубы увеличивается до ближайшего большего типового, и расчеты в последнем случае повторяются.
Если полученный подпор H ≤ ( Hнас - 0,5), то расчет трубы продолжается на наибольший расход Q m а kc
Следует иметь в виду, что в отдельных частных случаях при Q paсч труба может перейти из напорной в полунапорную, как изложено на стр. 27-28.
Рис. II .27. Схема трубы
Рис. II .28. Схема для определения длины трубы
Гидростатическое давление р внутри напорной трубы, значение которого необходимо для статического расчета конструкции (подбора толщины стенок трубы), определяется по Qмакс по формуле
|
|
( II.18) |
где H - подпертая глубина воды перед трубой.
Нижний бьеф напорной трубы рассчитывается согласно указаниям глав V и VI.
Расчет напорных труб при затопленном нижнем бьефе
Методика расчета напорных труб с затопленным выходным отверстием также построена на аналогии работы трубы и внешнего насадка, в котором происходит истечение воды под уровень (рис. II.29).
Значительная кинетическая энергия, развивающаяся в напорной трубе, способствует оттеснению уровня нижнего бьефа; поэтому такая труба начинает работать по схеме затопленного насадка только при достаточном возвышении уровня нижнего бьефа над верхом выходного отверстия трубы (рис. II.30), что проверяется выражением
|
|
( II.19) |
где ![]() - скорость течения в
нижнем бьефе;
- скорость течения в
нижнем бьефе;
v - скорость в трубе, работающей полным сечением при данном Н, или эмпирическим соотношением
|
hn = hбыТ - iL > 1,4 hTp |
( II.20) |
Обозначения в формулах ( II.19) и ( II.20) ясны из рис. II.30.
Для расчета затопленной в нижнем бьефе напорной трубы нужно, кроме Qмакс знать vдоп и Hдоп
Если задано vдоп, то диаметр определяют по формуле
|
|
( II.21) |
Полученное значение d округляют до ближайшего типового размера, после чего определяют фактическую скорость в трубе
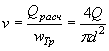
Рис. II .29. Схема работы затопленного внешнего насадка
Рис. II.30. Напорная труба при затопленном выходном отверстии
По скорости v определяется напор z
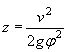
Где
![]()
Для расчетов можно принять ![]() = 0,5
= 0,5
![]()
Далее определяют подпор Н
|
Н = z - il + hбыт. |
( II.22) |
Если Н < Hдоп, то расчет на этом заканчивается. Если Н > Нлоп, то диаметр трубы нужно увеличить и повторить расчет снова.
Расчет затопленной трубы ведется также по Qмакс а именно:
1) задается ориентировочно диаметр трубы d;
2) определяют ожидаемый подпор перед трубой по следующей формуле, получаемой из уравнения ( II.15):
|
|
( II.23) |
Если hбыт < hTp, то в формулу ( II.23) вместо hбыт следует подставлять hт p;
3) определяют величину действующего напора
z= Н + iL - hбыт;
4) проверяют достаточность назначенного отверстия:
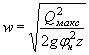
Для трубы круглого сечения данную проверку выполняют в отношении диаметра:
![]()
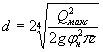
Значение jн принимают в зависимости от длины трубы по графику рис. II.25.
При совпадении потребного отверстия с заданным расчет продолжается (в противном случае расчет повторяется для другого отверстия);
5) определяют скорость на выходе:
![]()
ОСОБЫЕ СЛУЧАИ РАСЧЕТА ТРУБ
Поверочные расчеты по наибольшему расходу Qм aк c
Для каждой трубы (на железных дорогах) должна быть произведена проверка достаточности высоты насыпи над трубой при расходе Qм aк c (отверстия труб на железных дорогах, как указывалось выше, рассчитываются по двум расходам).
Порядок проверки достаточности возвышения бровки земляного полотна над подпертым уровнем при Qм aк c зависит от условий работы трубы при Qрасч.
Если при Qрасч подпор перед трубой H был менее 1,2 hrp, то сначала определяется подпор при (Знаке и проверяется соотношение между Нмакс и hTp.
Если Нмакс £ 1,2 hTp, то бровка проверяется на полученный Нмакс
Если Нмакс > 1,2 hTp, то прежде всего выясняется, какой именно режим может устанавливаться в трубе при Qм aк c - полунапорный или устойчивый напорный.
При полунапорном или неустойчивом напорном режиме подпор H вычисляется по полунапорному режиму по формуле ( II.12).
Устойчивый напорный режим получается при условии H н > H п, где H п определяется по формуле ( II.12), а Hн- по формуле ( II.15).
Эта проверка является наиболее простой из всех приведенных в литературе определений границ между напорным и полунапорным режимами.
Проверка возвышения бровки земляного полотна над Hмакс производится у наинизшей отметки бровки в пределах разлива; кроме того, производится проверка в отношении перелива в соседний бассейн.
Если расстояние от бровки земляного полотна до подпертого горизонта воды недостаточно, необходимо повысить насыпь в пониженной точке или уменьшить величину Hмакс, увеличив отверстие трубы. Иногда целесообразно отсечь часть бассейна дамбой для уменьшения расхода воды, поступающей в трубу, или сбросить часть расхода в соседний бассейн.
Расчет дюкеров
Дюкеры (трубы в выемках), как правило, устраиваются на зарегулированных водотоках, например оросительных каналах и поэтому их расчет сводится к подбору отверстия трубы по одному заданному расходу.
Так как труба дюкера всегда работает полным сечением, она, как правило, устраивается круглой (рис. II.31). В отдельных случаях, когда через дюкер, помимо нормального, периодически пропускаются повышенные паводочные расходы, дюкер может быть запроектирован из двух труб с ярусным расположением с тем, чтобы верхняя труба работала только при повышенных (паводочных) расходах (рис. II.32). В этом случае верхняя труба должна иметь затвор (шандор).
Для возможности осмотра колодцев их диаметр должен быть не менее 1 м (рис. II.33).
При одновременной проектировке дюкера и оросительного канала может быть рассмотрен вариант дополнительного понижения выхода из дюкера с соответствующим увеличением глубины канала за дюкером (для возможности увеличения Δ H).
Рис. II .31. Нормальное поперечное сечение дюкера
Рис. II .32. Поперечное сечение дюкера при ярусном расположении труб
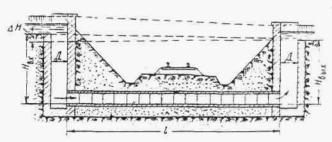
Рис. II .33. Схема дюкера
Исходные данные для расчета дюкера:
1) расход водотока Q м3/сек;
2) разность в отметках дна канала у входного и выходного колодцев дюкера (рис. II.34).
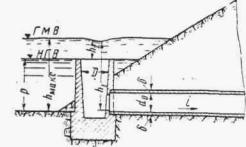
Рис. II .34. Схема приемного шахтного водосброса
Нвх - Нвых = Δ H
3) длина дюкера между колодцами L м.
Расчет дюкера должен производиться исходя из следующих положений:
Qдюк = Qканала
Δ H дюк = Δ Hканала
При заданном Δ H скорость воды в дюкере будет
|
|
( II. 24) |
где
![]()
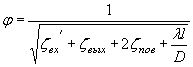
Если окажется, что vдюк ³ vканала, d диаметр дюкера определяется по формуле
|
|
( II.25) |
Для сохранения условия vдюк ³ vканала d следует округлять в меньшую сторону, но определять при этом новое значение Δ H:
|
|
( II.26) |
Расчет приемного шахтного водосброса
Устройство шахтного водосброса возможно при небольших расходах для образования небольших водохранилищ.
На основании испытании моделей шахтных водосбросов в Институте гидрологии и гидротехники Академии наук УССР расчет таких сооружений производится следующим образом.
Необходимую площадь поперечного сечения трубы под насыпью определяют по формуле
|
|
( II.27) |
где d - ориентировочно назначенный диаметр трубы;
i - уклон трубы;
L - длина трубы;
Hмакс-наибольшая допустимая глубина воды в пруду у сооружения, назначаемая в зависимости от высоты насыпи.
Как правило, назначается круглая железобетонная труба - по вычисленной w; принимается ближайшее типовое отверстие с площадью w 0 и диаметром d0.
Определяется коэффициент скорости
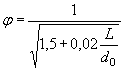
и расчетная глубина воды над дном шахтного колодца
|
|
( II.28) |
а также глубина воды в пруду над гребнем колодца
h2 = h1 - р (см. рис. II.34).
Минимальный диаметр колодца назначается из условия
D ³ d0 + 2 d.
Превышение, уровня воды над верхом колодца при проходе паводка
|
|
( II.29) |
где m - коэффициент расхода через приемный колодец, определяемый в зависимости от отношения h2/ D:
При h/ D > 0,2 колодец начинает работать как труба по типу истечения из внутреннего насадка, и в этом случае h2= h.
Если h2 > Hмакс - р, необходимо увеличить диаметр колодца и вторично определить h2.
|
h2/D |
m |
|
При h1 £ p |
0,42 |
|
0,1 |
0,38 |
|
0,2 |
0,34 |
ГЛАВА III
РАСЧЕТЫ МОСТОВ
ОБЩИЕ ПОЛОЖЕНИЯ
Русло под однопутным или двухпутным мостом по протеканию в нем водного потока аналогично модели водослива с широким порогом, если имеет место неравенство
![]()
Водослив с широким порогом может быть незатопленным, когда уровень нижнего бьефа не оказывает влияния на протекание воды по водосливу (рис. III. 1), и затопленным, когда уровень нижнего бьефа распространяется на водослив (рис. III.2).
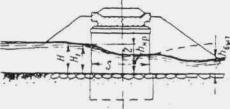
Рис. III . 1. Незатопленный водослив с широким порогом
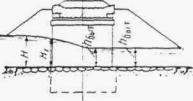
Рис. III .2. Затопленный водослив с широким порогом
Протекание воды под малым мостом можно отнести к одной из схем на основании сравнения бытовой глубины в отводящем русле hбыт с критической глубиной для подмостового сечения:
при hбыт £ 1,25 hкр - свободное истечение (незатопленный водослив);
при hбыт >1,25 hкр - несвободное истечение (затопленный водослив).
Общая расчетная формула расхода прямоугольного водослива имеет вид
|
|
( III.1) |
где т - коэффициент расхода незатопленного водослива;
b - ширина водослива поперек потока;
H0 - подпор перед мостом с учетом скорости подхода v0;
![]()
Формулу ( III.1) можно представить в виде
|
|
( III.2) |
где j - коэффициент скорости, принимаемый по табл. 4 приложения 12;
wкр - площадь живого сечения на водосливе, равная b/ lкр
hкр - глубина потока на водосливе,
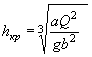 '
'
H0 - имеет прежнее значение.
При затопленном водосливе в формулу ( III.2) вместо hк p и wкр следует вводить hбыт и w = bhбыТ.
Величина отверстия моста должна быть такой, при которой скорость течения потока на выходе не будет размывающей при принятом типе крепления. От подпертого горизонта перед мостом до низа конструкции должны быть обеспечены запасы по табл. III. 1.
Таблица III.1
Наименьшие допускаемые возвышения низа конструкций мостов над подпорным уровнем
|
Наименование элементов мостов |
Наименьшее возвышение в м |
|||
|
над уровнем воды с учетом влияния подпора и волны |
над наивысшим уровнем ледохода |
|||
|
расчетным для мостов на дорогах |
наибольшим для мостов на железных дорогах |
|||
|
железных |
автомобильных и городских |
|||
|
Низ пролетных строений: |
|
|
|
|
|
а) при глубине подпертой воды не более 1м |
0,5 |
0,50 |
0,25 |
- |
|
б) при глубине подпертой воды более 1 м |
0,75 |
0,50 |
0,25 |
0,75 |
|
в) при наличии карчехода |
1,5 |
1,00 |
1,00 |
- |
|
г) на селевых потоках |
- |
1,00 |
1,00 |
- |
|
Подферменная площадка |
0,25 |
0,25 |
- |
0,50 |
|
Низ пят арок и сводов |
0,25 |
- |
- |
0,25 |
|
Низ продольных схваток и выступающих элементов конструкций в пролетах деревянных мостов |
0,25 |
0,25 |
- |
0,75 |
При проверке соблюдения требований неподтопляемости согласно табл. III.1 принимают величину подпора H, определенную по формулам ( III.5) или ( III.7). Однако следует отметить, что подпор H по этим формулам определяется не во входном сечении отверстия моста, а на некотором расстоянии вверх по течению (см. рис. III.1 и III.2).
В практике проектирования автодорожных мостов это обстоятельство учитывается и проверка производится не по H, а по H1 причем принимается, что H1 = 0,88 H. Коэффициент 0,88 принят на основании опытов В.В. Смыслова, согласно которым H1 = (0,75 ¸ 0,85) H. Вот почему при проектировании автодорожных мостов рекомендуется проверять наименьшее возвышение низа конструкции над подпертым уровнем H1, принимая H1 = 0,88 H.
РАСЧЕТЫ ОТВЕРСТИЙ МОСТОВ В ОБЫЧНЫХ УСЛОВИЯХ
Расчет отверстия моста начинается с определения типа водослива, для чего определяются критическая hкр и бытовая hбыт глубины.
При расчете по допускаемой скорости vдоп критическая глубина определяется по формуле
![]()
Бытовая глубина hбыт определяется методом последовательных приближений из уравнения Шези
![]()
где wбыт - площадь живого сечения потока в отводящем русле в бытовых условиях;
Rбыт - гидравлический радиус для бытовых условий;
Сбыт - коэффициент Шези;
i - уклон дна.
Если hбыт £ 1,25 hкр то водослив не затоплен, и расчет производится по формуле Бресса
|
|
( III.3) |
где Qр acч- расчетный расход;
e - коэффициент сжатия (см. табл. 4 приложения 12).
Если hбыт > 1,25/ hкр, то водослив затоплен, и расчет производится по формуле
![]()
Канд. техн. наук Виноградов предложил упрощенный способ определения характера водослива для малых мостов и безнапорных труб, основанный на сравнении фактического уклона дна отводящего русла i с критическим значением уклона i кр.
При i ³ iк p водослив не затоплен.
Для определения критического уклона дна русла применяется приближенная формула
iкр= 10 n2
где п - коэффициент шероховатости отводящего русла. Значения коэффициента шероховатости п по классификации Срибного и соответствующие значения критических уклонов приведены в табл. III.2
Таблица III.2
Коэффициент шероховатости п и критический уклон iкр для естественных русел
|
Характер русла водотока |
п |
i кр |
|
Периодические потоки (большие и малые) при очень хорошем состоянии поверхности ложа. |
0,033 |
0,011 |
|
Земляные русла периодических водотоков (сухих логов) в относительно благоприятных условиях |
0,040 |
0,016 |
|
Периодические (ливневые и весенние) водотоки, несущие во время паводка заметное количество наносов, с крупногалечным или покрытым растительностью (травой и пр.) |
0,050 |
0,025 |
|
Русла периодических водотоков сильно засоренные и извилистые |
0,067 |
0,045 |
При iк p> i водослив может быть затопленным или незатопленным.
Характер водослива в этом случае определяется сравнением расчетного расхода Qр acч с бытовым расходом Qбыт, который проходит в русле при бытовой глубине hбыт= 1,25 hк p.
При Qр acч .> Qбыт водослив затоплен; при Qр acч .< Qбыт водослив не затоплен.
Ниже приводятся примеры определения характера водослива по предложенному методу.
Пример 1. Определить характер водослива в отверстии малого моста прямоугольного сечения, если уклон отводящего русла i = 0.03. Ложе водотока покрыто крупной галькой и частично заросло травой.
Решение. По табл. III.2 критический уклон русла для заданных условий iкр= 0,025, так как имеет место неравенство i > iкр, протекание в отверстии сооружения будет происходить по типу незатопленного водослива.
Пример 2. Определить тип водослива в отверстии малого моста при следующих условиях: уклон дна отводящего русла i = 0,005. Сечение русла симметричное треугольное при коэффициенте откоса m = 4. Русло сильно засоренное и извилистое. Допускаемая скорость течения vдоп = 3 м/сек. Расчетный расход Q pacч = 5 м3/сек.
Решение. По табл. III.2 критический уклон для заданных условий i Kp = 0,045 > i = 0,005. Следовательно, тип водослива необходимо определять путем сравнения расходов.
Определяем критическую глубину в отверстии сооружений по допускаемой скорости
![]()
Бытовая глубина
hбыт = 1,25 hкр= 1,25·0,92 =1,15 м.
Площадь живого сечения русла
![]()
Смоченный периметр
![]()
Гидравлический радиус
![]()
Коэффициент Щези
![]()
Бытовой расход
![]() .
.
Имеем неравенство Qр acч .> Qбыт т. е. течение будет по типу затопленного водослива.
Порядок расчета по формуле Бресса следующий.
1. По данным расчета Qр acч и vяоп определяют необходимое отверстие моста по формуле ( III.3).
2. Полученное b округляют до ближайшего большего типового отверстия bтип.
3. Определяют критическую глубину
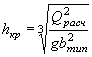
4. Проверяют затопление водослива (мостового отверстия) по неравенству hбыт £1,25/ hкр.
5. Если hбыт £1,25/ hкр подпор перед мостом определяют по формуле
|
|
( III.4) |
Практически в тех случаях, когда v0 < 1 м/сек, членом ![]() можно пренебречь.
можно пренебречь.
При j = 0,9 и v £ 1 м/сек выражение ( III.4) обращается в
|
H = 1,6 h кр |
( III.5) |
Подходная скорость менее 1 м/сек практически имеет место при ширине отверстия, меньшей 1/3 ширины бытового русла.
6. По табл. III.1 проверяют условия допустимости полученного отверстия моста bтип при данной высоте насыпи H нас.
Если высота насыпи окажется недостаточной, то принимают ближайшее большее типовое значение отверстия моста, вычисляют подпор и определяют достаточность высоты насыпи.
Расчет отверстия по схеме затопленного водослива производится по формуле ( III.4). Полученное значение округляется до ближайшего большего типового отверстия bтип.
По bтип находят скорость под мостом при бытовой глубине hбыт по формуле
|
|
( III.6) |
Подпор перед мостом определяют по формуле
|
|
( III.7) |
Если v0
£
1 м/сек, членом ![]() пренебрегают.
пренебрегают.
Затем проверяют по табл. III. 1 достаточность возвышения низа конструкции над расчетным и наибольшим подпорными уровнями. При недостаточном возвышении принимают ближайшее большее типовое значение отверстия и повторно проверяют достаточность выбранного отверстия.
Отверстия мостов на железных дорогах общей сети должны также рассчитываться по наибольшим и расчетным расходам Qмакс и Q pacч и соответствующим им уровням, а для мостов на автомобильных дорогах всех категорий и назначений отверстия мостов рассчитываются по расчетным расходам и соответствующим им уровням.
Бровка земляного полотна на подходах к малым мостам в пределах разлива должна возвышаться:
а) для железных дорог общей сети над отметкой подпертого уровня, соответствующего расходу Qмакс не менее чем на 0,5 м;
б) для автодорожных и городских мостов не менее чем на 0,5 м над отметкой подпертого уровня, соответствующего расчетному расходу Q pacч.
Во всех случаях при проверке сооружения на пропуск Qмакс не допускается перелив подпертой воды через водоразделы в ближайшие сооружения. Поверочные расчеты по Qмакс ведут в следующем порядке.
1. Определяют скорость течения под мостом
![]()
где e принимается по основному расчету.
2. Определяют критическую глубину при максимальном расходе
![]()
3. При hKp макс > 1,25/ hбыт макс водослив будет незатопленным (здесь hбыт макс - бытовая глубина, соответствующая Qмакс).
Нормы допускаемых скоростей течения воды при расчете на наибольший расход для железнодорожных мостов разрешается повышать на 20 %.
4. Определяют подпор перед мостом
Hмакс = 1,6 hк p макс
5. Проверяют отметку бровки полотна.
6. Проверяют отметку низа конструкции (см. табл. III.1)
Если в результате проверки одно из условий окажется несоблюденным, то весь расчет отверстия моста должен быть проведен вновь при новой (большей) величине отверстия или должен быть перепроектирован продольный профиль у моста.
7. Если окажется, что hк p макс <С 1,25 hбыт, то поверочный расчет на Qмакс ведется по формулам:
![]()
![]()
ПОВЕРОЧНЫЕ РАСЧЕТЫ ОТВЕРСТИЙ СУЩЕСТВУЮЩИХ МОСТОВ
Для данного моста (заданы отверстие b, конструкция моста, тип крепления лотка и высота насыпи Hнас) требуется определить гидравлические параметры.
Полагая водослив незатопленным, расчет ведется в следующем порядке.
1. Определяют наибольший допустимый расход
![]()
2. Вычисляют критическую глубину
![]()
3. Определяют тип водослива по неравенству
hк p ![]() 1,25 hбыт
1,25 hбыт
Если hKp ³ 1,25 hбыт. расчет продолжают в следующем порядке.
4. Определяют подпор по формуле ( III.4) или ( III.5).
5. Проверяют достаточность возвышения бровки полотна (см. стр. 40).
Если отметка бровки полотна достаточна, расчет считается законченным.
Если hбыт > l,25 hKp, расчет ведут для затопленного водослива. Глубину потока под мостом принимают равной глубине потока в отводящем русле hбыт (см. рис. III.2):
1. Определяют Q = b e hбыт vдоп, где e - коэффициент сжатия, зависящий от формы опор (см. табл. 4 приложения 12).
2. Определяют подпор по формуле ( III.7).
3. Проверяют достаточность возвышения бровки полотна.
НОМОГРАММЫ ДЛЯ РАСЧЕТА ОТВЕРСТИЙ МОСТОВ ТРАПЕЦЕИДАЛЬНОГО СЕЧЕНИЯ
Расчет трапецеидальных отверстий мостов методом последовательных приближений требует большой затраты времени. Номограммы канд. техн. наук Э.А. Гарбовского облегчают определение необходимых величин по заданному расходу и скорости.
Для построения номограммы при незатопленном режиме потока в отверстии моста принято общее уравнение критического состояния потока
![]()
Номограмма рис. III.4 связывает величины ![]() , hкр,
, hкр, ![]() , vKр
и величину перепада z (рис. III.3)
, vKр
и величину перепада z (рис. III.3)
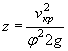
' 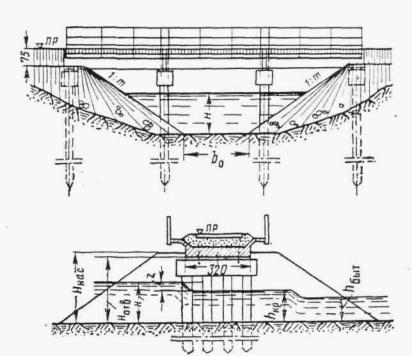
Рис. III .3. Схема моста с отверстием трапецеидального сечения
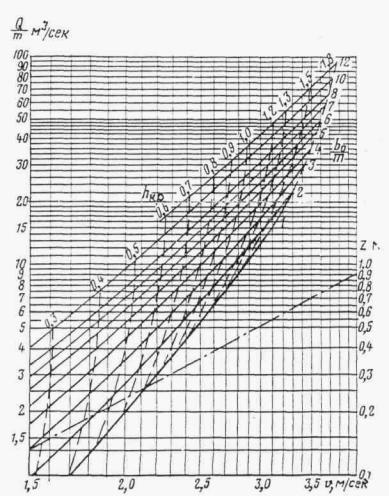
Рис. III .4. Номограмма для расчета трапецеидальных отверстий мостов при незатопленном режиме потока
Ключ пользования номограммой дан на рис. III.5.
При построении номограммы принято: а = 1,1; коэффициент скорости j = 0,95.
С учетом сжатия по номограмме величина расхода принимается исправленной на коэффициент сжатия. Стеснение отверстия промежуточными опорами свайно-эстакадных мостов учитывается добавлением суммарной их ширины к определенной по номограмме величине b0.
Для определения гидравлических элементов моста при условии его работы как затопленного водослива по уравнению
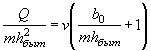
построена номограмма (рис. III.6).
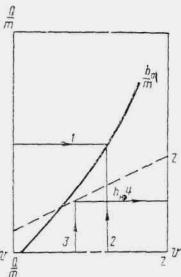
Рис. III .5. Ключ для пользования номограммой III .4
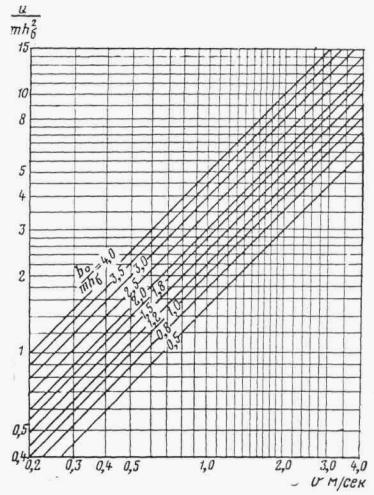
Рис. III .6. Номограмма для расчета трапецеидальных отверстий мостов при затопленном режиме
Порядок расчета по номограмме следующий. Принимается коэффициент сжатия потока e, коэффициент заложения откоса конусов под мостом т и в зависимости от крепления русла под мостом допускаемая скорость воды vдоп.
Вычисляют величину ![]() и по
номограмме рис. III.6
определяют для данного vдоп величину
и по
номограмме рис. III.6
определяют для данного vдоп величину ![]() . Если по заданным
. Если по заданным ![]() и v доп по номограмме на рис. III.4
и v доп по номограмме на рис. III.4 ![]() оказывается больше 12, а hбыт £ h кр целесообразно по экономическим соооражениям уменьшить
отверстие, увеличив vдоп за счет крепления
подмостового участка русла.
оказывается больше 12, а hбыт £ h кр целесообразно по экономическим соооражениям уменьшить
отверстие, увеличив vдоп за счет крепления
подмостового участка русла.
Получив b0, подбирают ближайшее для данной конструкции моста и высоты насыпи отверстие b0факт с учетом ширины промежуточных опор моста в плоскости, перпендикулярной потоку.
По принятому b0факт определяют vфакт, hк p и z; суммируя z и hKp, проверяют соблюдение условий неподтопления моста (см. табл. III. I):
( hк p + z) + 0,75 £ Hотв
В тех случаях, когда определенная по заданным ![]() и v величина
hк p оказывается
менее 1,25 hбыт, расчет ведется по
номограмме для затопленного водослива.
и v величина
hк p оказывается
менее 1,25 hбыт, расчет ведется по
номограмме для затопленного водослива.
Подбирают ближайшее конструктивное значение b0 определяя истинную скорость v течения воды под мостом и перепад z.
Вероятность подтопления в этом случае проверяют из условия
hбыт + z + 0,75 £ Hотв
ЧАСТНЫЕ СЛУЧАИ РАСЧЕТА МОСТОВ. МНОГОПРОЛЕТНЫЕ МОСТЫ
Формула для расчета отверстия многопролетного моста для незатопленного водослива имеет следующий вид:
|
|
( III.8) |
где ![]() - расстояние между
устоями;
- расстояние между
устоями;
![]() -размер отверстия однопролетного моста, определяемый по
общим правилам (без учета сжатия устоями);
-размер отверстия однопролетного моста, определяемый по
общим правилам (без учета сжатия устоями);
N - число боковых сжатий, равное удвоенному числу промежуточных опор плюс два сжатия от береговых устоев;
![]() - сумма
ширины быков;
- сумма
ширины быков;
x - коэффициент, зависящий от формы опор (рис. III.7):
а) для быков прямоугольного очертания x = 1;
б) для быков с полуциркульным или треугольным очертанием передней грани x= 0,7;
в) для быков с криволинейным заостренным очертанием передней грани x = 0,4.
Расчет многопролетных мостов ведется в следующем порядке:
1) по заданным расходам Q paсч и Qмакс и допускаемой скорости течения vдоп определяют отверстие однопролетного моста и его гидравлические характеристики hк p, и H;
2) по формуле ( III.8) определяют отверстие многопролетного моста Вм, у которого глубина hк p, подпор H и скорость течения vдоп такие же, как и у однопролетного моста.
Для улучшения гидравлических характеристик многопролетного моста, как показали опыты С. А. Офицерова, рекомендуется носовые части быков развивать вверх по течению на величину l (см. рис. III.7), равную половине значения напора перед мостом, т. е. l = 0,5 ( H - Hбыт).
В таком случае значения x равны:
для быков с прямоугольным очертанием - 0,5;
для быков треугольного и полуциркульного очертаний - 0,45;
для быков криволинейного заостренного очертания - 0,28.
Отверстие многопролетного моста для затопленного водослива определяют по формуле
|
|
( III.9) |
где Вм - расстояние между устоями.
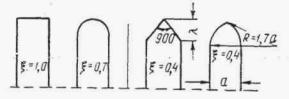
Рис. III .7. Очертания быков в плане
ОПРЕДЕЛЕНИЕ ОТВЕРСТИЙ МОСТОВ НА ЗАЛИВАХ ВОДОХРАНИЛИЩ
Сооружения, отделяющие залив водохранилища, пойменного озера, ильменя или лимана от его основной части, находятся в особых условиях, так как поток под сооружением периодически меняет направление в связи с колебаниями уровня речного бьефа (основной части водохранилища).
В момент равновесия уровней в бьефах потока через сооружение нет. При изменении уровня речного бьефа возникает перепад zt (рис. III.8).
Рис. III .8. Мосты на заливах водохранилищ: а - опорожнение; б - наполнение
При понижении уровня речного бьефа (спад паводка в реке, сработка рабочего объема водохранилища) отсеченная часть будет опорожняться (рис. III.8, а), а при повышении - наполняться через отверстие сооружения (рис. III.8 б).
Перепад в уровнях увеличивается (следовательно, увеличивается и скорость потока) до тех пор, пока скорость изменения уровня воды в отсеченной части не станет равна скорости изменения уровня речного бьефа, что соответствует максимуму скорости потока в отверстии моста.
Скорость изменения уровня в отсеченной части может и не достигнуть величины скорости изменения уровня речного бьефа до конца периода изменения уровней в интервале от H0 до H1 (см. рис. III.8); в этом случае максимум перепада установится в конце при достижении уровнем речного бьефа своего крайнего положения ( H1 при наполнении и H0 при опорожнении).
Канд. техн. наук Э.А. Гарбовским на основе общего уравнения баланса Q1 dt = Ftdh составлены дифференциальные уравнения, связывающие все показатели, характеризующие отсеченную часть, отверстие сооружения и скорость изменения уровня речного бьефа; на основе анализа этих уравнений получены соотношения, определяющие максимум перепада zt (следовательно, и скорости потока) в сооружении.
Численное интегрирование полученных дифференциальных уравнений для ряда конкретных параметров позволило построить расчетные номограммы для опорожнения (рис. III.9) и наполнения (рис. III.10).
При составлении номограмм учтены все вышеперечисленные случаи получения возможного максимума zt и влияние возможного изменения режима истечения из затопленного в незатопленный.
Порядок пользования номограммами следующий: по исходным данным F1, F0, H1, H0 и а вычисляются вспомогательные характеристики:
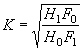 ;
;
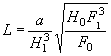 и
и ![]()
где а - расчетная скорость изменения уровня речного бьефа.
Нужно иметь в виду, что чем больше а, тем больше требуется отверстие моста для сохранения допустимой скорости (при прочих равных условиях).
При вычислении вспомогательных характеристик следует принимать F в км2, Н в м, а в м/сутки.
При заданной допускаемой скорости определяется величина максимально допускаемого относительного перепада
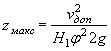
где j - коэффициент скорости, принимаемый по табл. 4 приложения 12.
Рис. III .9. Номограммы для опорожнения
Рис. III . 10. Номограммы для наполнения
По относительному перепаду z1,
и вычисленным K и L для
соответствующих п определяют величину относительного отверстия ![]() . Отвер cтие
. Отвер cтие
![]()
Номограммы составлены для К ³ 1. В некоторых случаях характеристика К может оказаться менее единицы. В этом случае необходимо принимать
К = 1 и 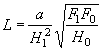
Расчетную величину скорости изменения уровня речного бьефа а можно принимать средней (рис. III.11, а)
![]()
где T - продолжительность изменения уровней от Н0 до Н1.
Расчетные величины F0 и F1 по кривой Ft = f( H) на участке от H0 до Н1 существенно отличающейся от прямой, необходимо принимать (для большей точности расчета) с поправками, пользуясь следующим методом.
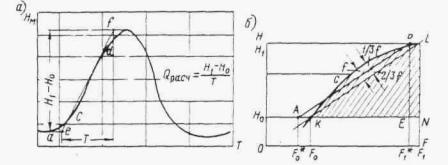
Рис. III .11. Определение a с р и поправок к F 0 и F 1
Между точками кривой F = f( H), соответствующими Н0 и Н1 проводят хорду и параллельную ей секущую на расстоянии 2/3 высоты сегмента (рис. III. 11,6). В этом случае площадь ΔАВЕ » площади фигуры KCLN. На пересечении этой секущей с абсциссами Н0 и Н1 получены точки расчетных величин F *0 и F*1
Определяющим фактором для выбора характера расчетной номограммы является величина интенсивности изменения уровня речного бьефа а (если при наполнении а значительно больше, чем при опорожнении, то за расчетный случай следует принимать наполнение). При величинах а, близких по величине как для наполнения, так и для опорожнения, целесообразно провести определение отверстия моста для обоих случаев и выбрать наибольшее.
Приведенные номограммы построены без учета дополнительных расходов, в некоторых случаях поступающих или отбираемых из отсеченной части, помимо рассчитываемого сооружения (испарение с зеркала отсеченной части в южных районах, расходы на орошение, постоянный приток в отсеченную часть и т. п.).
Э. А. Гарбовский предложил учитывать влияние дополнительного расхода, вводя его в расчет в виде средней постоянной величины поправки к скорости изменения уровня отсеченной части:
 в размерности a
в размерности a
Где
![]()
тогда величина отверстия с учетом дополнительного расхода
![]()
где b - величина отверстия, определенная по номограммам без учета дополнительного расхода.
Невыгодными расчетными случаями, когда р принимается со знаком (+). являются:
а) при опорожнении - приток дополнительного расхода в отсеченную часть;
б) при наполнении - забор воды из отсеченной части.
Ниже приводятся примеры определения требуемых отверстий мостов при наполнении и опорожнении.
Пример 1. Повышение уровня речного бьефа 0,2 м/сутки (наполнение); vдоп = 2,5 м/ сек; H1 = 3 м; H0 = 1 м; F0 = 6 км2; F1= 12 км2; j = 0,9; e = 0,85. Находим n = 1/3= 0,33;
![]()
![]()
По номограмме находим ![]() =1,6, откуда искомое
=1,6, откуда искомое ![]() = 1,6 H1= 4,8;
= 1,6 H1= 4,8;
![]() .
.
Следовательно, применительно к типовым размерам необходимо принять b = 6 м.
Пример 2. Средняя скорость понижения уровня в речном бьефе а = 0,25 м/сутки; H1 = 2 м; H0 = 1 м; F0 = 5 км2; n = 0,5; ε = 0,9
![]()
![]()
Принимаем К = 1. Тогда
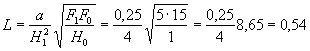
По номограмме для опорожнения (см. III.9) находим ![]() = 5,1, откуда
= 5,1, откуда ![]() = 10,2 м;
= 10,2 м;
![]() м
м
Установлено, что в расчетный период испарение с зеркала отсеченной части составляет 5 см/сутки.
Тогда расчетное отверстие
![]() м
м
Принимаем bдоп = 8 м.
Номограммы позволяют находить расчетную величину отверстия моста без подбора, а также пригодны для расчета отверстий трапецеидальных мостов.
В этом случае вычисленная ширина моста принимается как средняя между глубинами H1 и H0.
Ширина моста по дну равна
b 0 = b -m(H1 - H0).
Многопутные мосты
Особенностью гидравлического расчета многопутных мостов является то, что русло под ними не может быть принято горизонтальным и что в них может быть нарушено условие водослива с широким порогом 8 ³ S/ H >2,5 (см. рис. III.1).
Расчет таких мостов рекомендуется вести в следующем порядке:
1) пользуясь формулами ( III.3) и ( III.4), определяют b и Н
2) проверяют соотношение S : H и в случае, если S > 8 H, переходят на расчет, аналогичный расчету прямоугольной трубы.
Следует иметь в виду, что отверстие b,. принятое по типовым проектам мостов, при расчете моста как трубы может оказаться завышенным и, следовательно, режим под таким мостом - режимом затопленного водослива.
Если неравенство hбыт > 1,25 hкр удовлетворяется, то расчет моста следует проделать вновь как для трубы при затопленном нижнем бьефе.
В некоторых многопутных мостах, как, например, в мостах под широкой станционной площадкой, не удается выдержать должный уклон лотка i кр. В таких случаях отверстия многопутных мостов следует рассчитывать как безнапорные трубы с уклоном i < i кр.
АРОЧНЫЕ МОСТЫ
При расчетах арочных мостов различают два случая прохождения паводка
1) пяты свода не подтопляются (при Q paсч);
2) пяты свода подтопляются (при Qм akc).
К учету этих двух случаев и сводятся особенности расчета арочных мостов.
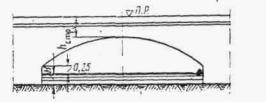
Рис. III . 12. Отверстие арочного моста при незатопленных пятах свода

Рис. III .13. Отверстие арочного моста при затопленных пятах свода
При расчетном расходе водотока Q pacч пяты свода не должны подтопляться (рис. III. 12) и допускаемое значение глубины подпертой воды перед мостом в этом случае определяется по формуле
|
Ндоп = Ннас - hстр - f - 0,25 |
( III.10) |
где Hнас - высота насыпи;
hстр - строительная высота конструкции арки в ключе, считая от подошвы рельса до низа арки;
f - стрела подъема арки.
В случае если пяты свода подтопляются при Qм akc (рис. III. 13), допускаемое значение глубины подпертой воды перед мостом определяется по формуле
|
Ндоп = Ннас - hстр - 0,5 f |
( III.11) |
Где 0,5 f должно быть не менее 1 м, т. е. 0,5 f ³ 1 м.
Кроме того, в этом случае надлежит учитывать дополнительный подпор перед мостом, образующийся вследствие сужения отверстия в пределах свода. Площадь живого сечения под мостом w определяется как сумма прямоугольника w1 и отрезка сегмента свода w2 (см. рис. III.13).
Исправленное значение скорости под мостом вычисляется по формуле
![]()
Исправленное значение h ¢к p определяют по формуле
![]() '
'
соответственно значение H- по формуле
![]() .
.
МОСТЫ-ВОДОСПУСКИ
В практике железнодорожного строительства иногда встречаются мосты с затворами, обычно называемые шандорными. Эти мосты имеют приспособления для перекрытия отверстия и предназначаются для работы только при определенном уровне воды в верхнем бьефе.
Если приспособление для перекрытия устроено в виде шандорного затвора, тогда отверстие моста работает по схеме водослива с острым порогом (рис. III.14).
Если приспособление для перекрытия устроено в виде подъемного щита, то отверстие моста работает по схеме истечения из-под щита (рис. III.15).
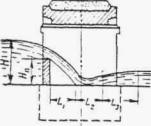
Рис. III .14. Мост-водоспуск с шандорным затвором
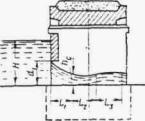
Рис. III .15. Мост-водоспуск с подъемным щитом
Мосты-водоспуски работают на строго зарегулированный расход, определяемый уровнем верхнего бьефа и степенью открытия затвора. Во всех случаях эти мосты работают по схеме незатопленного водослива, так как они включаются в работу только при условии понижения уровня в нижнем бьефе ниже уровня затвора.
Первый тип мостов-водоспусков - шандорные мосты - рассчитывают по формуле водослива с тонкой стенкой
|
|
( III.12) |
Значения коэффициентов водослива стойкой стенкой определяют по формуле
|
|
( III.13) |
и приведены в приложении 17.
Значение H в шандорных мостах невелико и определяется высотой одного или пары шандоров; практически эта высота колеблется от 0,14 до 0,7 м.
Для шандорного моста приходится решать следующие задачи:
а) по заданному времени опорожнения верхнего бьефа и высоте подпора на водосливе H определить потребное отверстие моста b;
б) по принятому отверстию моста b и высоте подпора на пороге H определить расход моста и время, потребное для опорожнения верхнего бьефа.
За порогом шандорного затвора образуется перепад (см. рис. III.14), для которого должны быть рассчитаны условия в нижнем бьефе.
Расчету подвергается случаи смятия самого верхнего шандора, когда струя, сливающаяся с затвора, имеет самую большую высоту падения.
Длину падения струи по сливу с гребня затвора можно определять по упрощенной формуле
|
l 1 = Нп + hкр, |
( III.14) |
где hкр определяют (по расходу на пороге Q) по формуле (1.15).
Длину прыжка определяют по формуле
|
l 3 = 2 hкр . |
(III.15) |
Длина отгона прыжка
|
|
( III.16) |
где iкр определяют по формуле (1.17), а
![]() .
.
Таким образом, полная длина укрепленного флютбета за шандорным затвором
L = l 1 + l 2 ,+ l 3
Далее (за прыжком) поток приобретает бытовую глубину и русло не нуждается в укреплении.
За расчетную скорость следует принимать скорость в сжатом сечении, т. е.
![]()
Зона русла возможного падения струи, т. е. на протяжении l 1 должна быть усиленно укреплена.
В мостах-водоспусках нет надобности принимать особые меры по гашению энергии потока, затоплению прыжка и т. п., так как они обычно работают на пропуск расчетных расходов редко и непродолжительное время.
Второй тип мостов-водоспусков - щитовые мосты - рассчитывают по формуле истечения воды из-под щита в незатопленный нижний бьеф
|
|
( III.17) |
где m - принимается по А.Н. Ахутину 0,63-0,64 при вертикальном расположении плоского щита;
а1 - высота подъема щита;
z -возвышение уровня верхнего бьефа над свободной поверхностью потока в нижнем бьефе в сжатом сечении (см. рис. III. 15).
Глубина в сжатом сечении
hсж = eа,
где а - высота отверстия;
e- коэффициент вертикального сжатия ( e = 0,64).
Далее определяют скорость в нижнем бьефе в сжатом сечении по
формуле ![]() и по ней принимают соответствующий тип крепления нижнего
бьефа.
и по ней принимают соответствующий тип крепления нижнего
бьефа.
Уравнение ( III.17) решается для первоначального положения уровня в верхнем бьефе, как для наиболее ответственного. По мере вытекания из-под щита уровень в верхнем бьефе будет падать и условия в нижнем бьефе будут облегчаться. Это в свою очередь позволит постепенно поднимать щит и, таким образом, поддерживать постоянный расход Q.
ОПРЕДЕЛЕНИЕ ОТВЕРСТИЙ ИСКУССТВЕННЫХ СООРУЖЕНИЙ НА СОРОВЫХ УЧАСТКАХ ТРАССЫ
Соры представляют собой замкнутые котловины, вытянутые в одном направлении (рис. III. 16). С точки зрения определения отверстий искусственных сооружений на соре возможны два принципиально различных случая пересечения их трассой железнодорожной линии.
В первом случае трасса уложена на склоне бассейна, тяготеющего к сору. Вода к насыпи будет подходить только с одной стороны, расчетный приток определяется обычным путем. Во втором случае, когда трасса пересекает непосредственно котловину сора, картина притока существенно изменяется:
вода притекает с двух сторон, поток трансформируется за счет аккумуляции, максимальный расход уменьшается, но продолжительность истечения увеличивается.
Рис. III .16. План сорового участка
Рис. III . 17. Схематическое изображение сора
Инженером Р.В. Зайцевым путем ряда выкладок, произведенных при схематическом изображении сора в виде комбинации поверхностей двух половин усеченных конусов, соединенных гранями трапецеидальной призмы (рис. III. 17), рекомендованы следующие типы и отверстия искусственных сооружений.
В первой зоне от точки В до сечения 4-4 (рис. III. 17, а) искусственного сооружения предусматривать не нужно, так как площадь бассейна настолько мала, что вся притекающая с него вода испарится до того, как сможет нарушить устойчивое состояние земляного полотна.
Во второй зоне (между сечениями 4-4 и 5-5) необходимо предусмотреть искусственное сооружение. Здесь целесообразны круглые железобетонные трубы с минимальным диаметром, а при недостаточной высоте насыпи - железобетонные лотки.
В третьей зоне (от сечения 5-5 до уреза воды, устанавливающегося в соре) следует предусматривать другие типы искусственных сооружений. Имея в виду возможность затопления сора водой и сохранения ее до заморозков, применение труб здесь нежелательно. Если нижняя часть труб будет расположена ниже уровня воды, то при определенных условиях трубы могут быть разрушены расширяющейся при замерзании водой.
Трубу можно предусматривать, не опасаясь за ее сохранность, в случае, когда экономически оправдан вынос ее на склон сора с тем, чтобы исключить попадание воды в нее перед заморозками. В противном случае следует строить железобетонные мосты отверстием не менее 2 м.
В четвертой зоне (от сечения 1-1 до сечения 2-2, находящегося между вершиной конуса и серединой сора при одинаковом слое осадков с обеих сторон насыпи, и от сечения 2-2 до сечения 3-3 при разном слое осадков) необходимость постройки искусственного сооружения должна быть обоснована. Если окажется, что его нужно строить, то следует руководствоваться рекомендациями, предлагаемыми для третьей зоны.
ГЛАВА IV
РАСЧЕТЫ ОТВЕРСТИЙ МАЛЫХ МОСТОВ И ТРУБ С УЧЕТОМ АККУМУЛЯЦИИ
ОБЩИЕ ПОЛОЖЕНИЯ
Расчеты отверстий малых мостов и труб с учетом аккумуляции при преобладающем ливневом стоке производятся во всех случаях, а при преобладающем снеговом стеке - только при отсутствии возможности заносов снегом оврагов перед сооружениями.
Аккумуляция не учитывается в районах с продолжительными ливнями (районы Приморья, Дальнего Востока, Черноморского побережья Кавказа, Прикарпатья и др.), а также при расчетах отверстий сооружений по расходам селевого, ледникового, грунтового и маревого стоков.
Уменьшение расходов в сооружениях за счет аккумуляции допускается более чем в три раза.
Расчеты отверстий малых сооружений с учетом аккумуляции по расходам ливневого стока производятся упрощенным или уточненным графическим способом.
Упрощенный способ применяется:
а) для предварительных соображений в предпроектных стадиях проектирования;
б) во всех стадиях проектирования местных автомобильных дорог;
в) во всех случаях проектирования железных и автомобильных дорог, если уменьшение расчетных ливневых расходов при учете аккумуляции не превышает 30 %.
Уточненный способ применяется во всех стадиях проектирования железных и автомобильных дорог, если уменьшение расчетных ливневых расходов при учете аккумуляции равно или больше 30 %.
Расчет отверстий малых искусственных сооружений с учетом аккумуляции по расходам снегового стока, если такой учет аккумуляции допустим, производится также двумя способами: по упрощенной формуле или графо-аналитическим способом.
Упрощенная формула применяется:
а) для предварительных соображений в предпроектных стадиях проектирования;
б) во всех случаях проектирования местных автомобильных дорог.
Графо-аналитический способ расчета может применяться во всех стадиях проектирования железных и автомобильных дорог.
Для расчетов отверстий малых искусственных сооружений с учетом аккумуляции необходимы следующие данные:
а) наибольший ливневый расход и соответствующий ему объем стока принятой вероятности превышения для расчетов упрощенным способом и дополнительно к этим данным - расход и соответствующий ему наибольший объем ливневого стока для уточненного способа;
б) уклон главного лога и его откосов перед сооружением и эскиз очертания пруда перед сооружением для расчетов упрощенным способом; план в горизонталях в пределах затопления местности подпертой водой перед сооружением для расчетов уточненным или графо-аналитическим способом;
в) графики водопропускной способности малых искусственных сооружений для обоих способов расчета.
В приложениях 18-24 приведены графики, составленные для труб любой длины с уклоном, большим или равным критическому, и труб, длина которых меньше пятикратной величины подпора перед сооружением, при уклоне лотка, меньшем критического.
Графики построены по формуле
|
|
( IV.1) |
где Q coop - расход в сооружении в м3/сек;
m - коэффициент расхода, зависящий в основном от очертания входного оголовка трубы или конусов моста;
w - площадь живого сечения потока с критической глубиной при безнапорном протекании, или площадь полного сечения трубы при напорном протекании, в м2;
g - ускорение силы тяжести, равное 9,81 м/сек2;
H - подпертая глубина воды перед сооружением над отметкой входа (лотки или укрепления) в м;
h - критическая глубина при безнапорном протекании, или сжатая глубина при напорном протекании, в м.
Если уклон сооружения меньше критического, а длина больше пятикратной величины подпора, пропускная способность сооружений зависит от размеров отверстия, длины, уклона и шероховатости лотка или русла. В таких случаях зависимости расходов от подпора перед сооружениями должны строиться на основании соответствующих гидравлических расчетов.
УПРОЩЕННАЯ ФОРМУЛА (ПРИ РАСЧЕТАХ ПО СНЕГОВОМУ СТОКУ)
При допустимости учета аккумуляции в указанных выше случаях по упрощенной формуле расход в сооружении принимается равным 0,65 максимального снегового расхода расчетной вероятности превышения:
|
Q coop = 0,65 Qснег . |
(IV.2) |
ГРАФО-АНАЛИТИЧЕСКИЙ РАСЧЕТ АККУМУЛЯЦИИ ВЕСЕННЕГО СТОКА
При наличии рельефа местности, способствующего значительной аккумуляции (обширные равнинные поверхности с малыми продольными и поперечными уклонами) может происходить аккумуляция снегового стока. Эту аккумуляцию можно учитывать, если в данном районе сильные заносы снегом оврагов представляют редкое явление. Отсутствие заносов, кроме наблюдений или показаний старожилов, может определяться отсутствием ветров в данном районе в зимний период, отсутствием растительности, задерживающей снег, малой глубиной пересекаемых логов и большой (а > 30 °) крутизной берегов логов.
Расчет аккумуляции весеннего стока (от таяния снега) следует производить графо-аналитическим способом «палетки». Новым в этом расчете является построение «пилообразного», схематизированного гидрографа снегового стока, изменяющегося по дням паводка 1.
1 См. сообщение ЦНИИС № 99 «Указания по расчету отверстий искусственных сооружений с учетом аккумуляции», 1958.
Схематизированный гидрограф снегового стока за период паводка может быть построен, исходя из следующих предположений.
1. Гидрограф строят в виде ряда суточных подъемов и спадов соответственно усилению снеготаяния в дневную часть суток и ослаблению снеготаяния ночью.
2. Максимальное значение снеговых расходов в течение суток достигается к 15 ч (днем), минимальное - к 7 ч (утром).
3. Число подъемов гидрографа соответствует среднему числу дней в снеговом паводке, которое определяется по наблюдениям на метеорологических станциях или по показаниям старожилов.
4. Максимальный расход при пике паводка гидрографа равен снеговому расходу Qсн расчетной повторяемости превышения, вычисленному по нормам ВСН 63-61.
5. Минимальное значение утренних расходов снегового стока падает до 1/4 дневных расходов.
6. Отдельные суточные максимальные расходы сперва по прямолинейной зависимости возрастают до наибольшего снегового расхода Qсн, затем также убывают.
7. Число дней подъема и спада снегового стока принимается равным.
Пример построения «пилообразного» гидрографа снегового стока за период паводка показан на рис. IV.1.
Рис. IV . 1. Гидрограф снегового стока
ГРАФО-АНАЛИТИЧЕСКИЙ МЕТОД РАСЧЕТА
Метод расчета основывается на последовательном решении уравнения водного баланса при аккумуляции
|
Wnр = Wсоор + Wак, |
( IV.3) |
где Wnp - объем воды, притекшей к сооружению за определенный промежуток времени; ^
Wсоор - объем воды, пропущенной сооружением за тот же промежуток времени;
Waк - объем воды, задержавшейся перед сооружением вследствие того, что Wсоор< Wnр
Это уравнение иллюстрируется эпюрой объемов притекшей, пропущенной и задержавшейся (аккумулированной) воды (рис. IV.2).
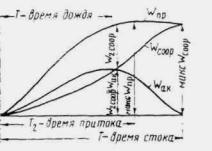
Рис. IV .2. Эпюра объемов притекшей, пропущенной и аккумулированной воды
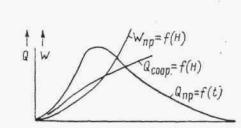
Рис. IV .3. График гидрографа притока, объемов воды и расхода в сооружении
Излагаемый ниже метод основан на общем уравнении водного баланса, решенном в отношении Wax:
ΔWак = Wnр - Wсоор = Q np Δ t - Q coop Δ t = ( Q np - Q coop) Δ t.
Сущность метода сводится к следующему (рис. IV.3):
1) строят кривую действительной аккумуляции перед сооружением в функции времени по уравнению
|
ΔWак = ( Q np - Q coop) Δ t |
( IV.4) |
2) на полученной кривой фиксируют значение WaK и соответствующий ему подпор Н, строят кривую расходов сооружения в функции времени
Q np = f(t).
Из серии гидрографов притока выбирают невыгоднейший, и подобно тому, как это пояснялось в предыдущем параграфе, строят кривые зависимости Wnp= f( H), Qсоо p= f( H).
Если все эти три кривые совместить на общей координатной сетке, то получится график, на котором будут одновременно изображены три исходные кривые:
гидрограф притока Q np = f( t);
кривая объемов воды перед сооружением Wnp = f( H);
кривая расхода в сооружении Q coop = f (Н) (см. рис. IV.3).
Для выполнения всех дальнейших построений и нахождения Q coop необходимо знать начальное значение аккумулированного объема перед сооружением Waк в функции времени Waк = f( t), которое принимается равным нулю1.
Располагая указанными данными, ведут построение на графике кривой WaK = f( t), для чего учитывают следующее обстоятельство: тангенс угла а наклона линии WaK (строго говоря, касательной к этой линии) на участке элементарного интервала времени Δt равен
|
|
( IV.5) |
В то же время, если уравнение ( IV.4) написать в отношении элементарного интервала времени, оно примет вид
ΔWак = ( Q np - Q coop) Δ t
Тогда
|
|
( IV.6) |
Другими словами, наклон линии WaK на данном участке характеризуется разностью Q np и Q coop , являющейся в графической интерпретации катетом прямоугольного треугольника с углом а.
Другой катет треугольника d должен быть принят в зависимости от соотношения масштабов расхода Q, объема W и времени t, т. е. если, например, масштаб Q - 1 м3/сек = п мм; масштаб W - 1 м3 = т мм, масштаб t - 1 сек мм, то катет d должен быть получен из уравнения
![]()
Так как расход принято исчислять в м3/сек, то и формула безразмерной величины d будет справедлива при t, измеряемом в секундах.
Для того чтобы она была справедлива при другом значении
Δ l, правую часть равенства нужно разделить на соответствующее
число секунд. Так, например, при Δ t = 1 мин ![]() и т. д.
и т. д.
Гипотенуза треугольника с катетами ( Q np - Q coop) и d определит на графике наклон линии WaK за рассматриваемый промежуток времени (рис. IV.4).
1 По последним исследованиям Ю. И. Даденкова и А. А. Кургановича гидрограф расходов в сооружении вначале следует принять равным гидрографу притока.
Таким образом, если через полученную ранее точку линии WaK провести линию, параллельную гипотенузе, и продолжить ее до начала следующего интервала времени, то ордината точки ее пересечения с ординатой конца данного интервала времени будет представлять значение WaK к концу интервала tn.
Таким образом можно построить всю кривую WaK в виде ломаной пинии состоящей из коротких прямых отрезков. При этом построении значения ( Q np - Q coop). Для каждого интервала времени будут разные, а значение d- постоянным.
На правом графике наносят исходные данные - кривые Wnp и Q coop в функции глубины H и на левом - гидрограф притока Q np = f( t).
Построение производят в следующем порядке.
Прежде всего по приближенному методу подбирают тип и отверстие сооружения.
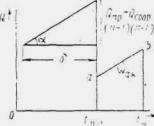
Рис. IV .4. Вспомогательный график
Рис. IV .5. График Q = f (Н), Wnp = f (Н) и Q np = f ( t )
Затем, принимая WaK = 0, выполняют построение исходя из следующих соображений: если к моменту tn-1 при данном отверстии сооружения b объем притекшей воды окажется W np, то этому последнему на правом графике будет соответствовать глубина H; при такой глубине через сооружение будет проходить расход Q coop, который за тот же промежуток времени Δ tn-1 составит объем W coop = Q coop t; тогда объем аккумулированной воды перед сооружением составит WaK = W np ( n-1) ,что и будет требуемой точкой а на графике.
На графике рис. IV.5 отрезок г g равен разности Q np - Q coop , откладывается значение d (линия ge); параллельно наклонной прямой ге проводят прямую из точки а аккумулятивного объема в момент tn-1; пересечение этой прямой в точке b с ординатой tn даст значение WaK в конце интервала Δ tn; точку b сносят на кривую Wnp правого графика и читают на нем значение H, отвечающее данному Wnp, и Q coop, отвечающее полученному H; точку Q coop сносят на ординату tn (см. рис. IV.4) левого графика и читают значение ( Q np - Q coop) в момент tn; пристраивая d к новому отрезку ( Q np - Q coop) путем параллельного переноса, получают новый отрезок кривой WaK и т. д.
Построение продолжается до тех пор, пока не будет вычерчена ветвь кривой аккумуляции до пересечения с ветвью гидрографа притока.
Как было отмечено выше, ордината точки пересечения кривой аккумуляции с гидрографом притока и будет представлять собой значение наибольшего расчетного расхода данного отверстия с учетом аккумуляции.
Кривую Q Coop строят на том же графике одновременно с кривой WaK путем соединения точек значений Q coop, получаемых при построении кривой WaK.
Для упрощения операций по сносу точек и проведению параллельных линий, а также во избежание построений треугольников eг g у каждой ординаты гидрографа Н. Н. Чегодаевым предложен графический прием, связанный с применением особой графической фигуры, вычерченной на прозрачной бумаге - палетке. При этом операции по переносу точек кривых W np = f (Н ) и Q coop = f( H) параллельно оси абсцисс заменяются операцией переноса и наложения палетки, на которой для этой цели нанесены кривые Wnp, и Q coop (рис. IV.6).
Операция проведения касательной к кривой WaK = f( t)
с наклоном ![]() заменяется операцией
ориентировки палетки под соответствующим углом наклона, причем tga принимается равным отрезку линии Q np - Q coop
заменяется операцией
ориентировки палетки под соответствующим углом наклона, причем tga принимается равным отрезку линии Q np - Q coop
Идея применения палетки такова: если на прямоугольнике
произвольной длины и высотой ![]() из одного угла
провести серию лучевых линий (см. рис. IV.6) и на них откладывать равномерно возрастающие значения ( Q np
- Q coop)
то концы лучей образуют плавную кривую, между которой и осью палетки O1 O2 и будут
заключаться все возможные значения Q coop.
из одного угла
провести серию лучевых линий (см. рис. IV.6) и на них откладывать равномерно возрастающие значения ( Q np
- Q coop)
то концы лучей образуют плавную кривую, между которой и осью палетки O1 O2 и будут
заключаться все возможные значения Q coop.
Рис. IV .6. Палетка при d = 83,3 мм
Рис. IV .7. Дополнительный график к палетке
Для построения «хвоста» эпюры WaK, когда значения WaK уменьшаются, следует построить зеркальное изображение кривой палетки, после чего она примет вид, изображенный на рис. IV.7.
Если лучевую линию палетки, имеющую данное значение ( Q np - Q coop) совместить на левом графике с отрезком ( Q np - Q coop), то наклон оси палетки ОО1 будет соответствовать наклону линии WaK в данном интервале времени.
Далее на палетку наносят линии Wnp и Q coop. Для этого, например, из точки b палетки проводят прямую под углом 45° к ее оси О1О2 и на эту прямую наносят значения Wп p из правого графика рис. IV.5, а затем на ординатах палетки от значений Wп p откладывают соответствующие значения Q coop .На этом построение палетки в основном заканчивается. Для облегчения пользования палеткой рекомендуется провести на ней ряд линий, параллельных оси О1О2.
Для практического применения палетки ее надо вычертить на прозрачной кальке и, последовательно накладывая на ординаты гидрографа стока (левый график рис. IV.5), строить на нем кривые.
Работа с палеткой производится в следующем порядке.
Точку O 1 прозрачной палетки совмещают с точкой у на ординате tn-1 первого числового значения WaK (левый график рис. IV.5) и вращают палетку до тех пор, пока ее ветвь не совпадет с точкой г. Этим будет определен наклон линии аЬ кривой WaK в интервале времени tn-1 - tn.
Затем ориентируют палетку так, чтобы ее ось О1О2 стала параллельной оси t, и совмещают точку данного значения WaK на палетке с точкой а на графике. На соответствующей ординате читают значение Q coop
Поступая подобным образом, на ординате tn постепенно строят весь график WaK и Q coop.
Как во всяком графическом методе, так и в данном требуется подбирать масштабы ( n, т и р) с таким расчетом, чтобы построение кривых было наиболее удобным и точным, наиболее точно засекались линии под углами, близкими к прямому.
ГЛАВА V
РАСЧЕТЫ НИЖНЕГО БЬЕФА
ОБЩИЕ ПОЛОЖЕНИЯ
Практика эксплуатации малых искусственных сооружений показала, что вследствие неправильного назначения размеров и конструкций укреплений отводящих русел затрачиваются очень большие средства на мероприятия по обеспечению устойчивости труб, малых мостов и насыпей около них от подмывов со стороны нижнего бьефа во время паводков.
Так как выходные скорости достигают 5-7 м/сек и поток, как правило, по выходе из сооружения находится в бурном состоянии, отводящее русло подвергается значительным размывающим воздействиям; поэтому правильное проектирование его укрепления имеет не меньшее значение, чем определение величин отверстий искусственных сооружений.
Вопросам расчета нижнего бьефа посвящен ряд специальных работ О.В. Андреева, М.С. Вызго, Д.И. Кумина, И.К. Поклонского. И.А. Шеренкова, Г.И. Сухомела, Л.Г. Бегама и В.С. Муромова.
В последних работах особое внимание уделяется тому обстоятельству, что широко распространенная методика расчетов укрепления нижнего бьефа водопропускных сооружений при определении скоростей в нижнем бьефе использует закон количества движения, в результате чего эти скорости получаются меньше фактических скоростей на выходе из трубы.
Часто назначают тип укрепления нижнего бьефа по выходной скорости из отверстия моста или трубы. Такие допущения справедливы только при растекании спокойного потока в широком нижнем бьефе, т. е. при подтоплении выходного отверстия сооружения.
В случае же растекания бурного потока по выходе из отверстия сооружения скорости в нижнем бьефе получаются большими, чем выходные скорости. Согласно исследованиям канд. техн. наук О. В. Андреева укрепление следует рассчитывать по скорости на выходе, увеличенной в 1,5 раза, т. е. v= 1,5 vвы x
Так как vвы x =
![]() (где Н -
подпор перед сооружением), получаем
(где Н -
подпор перед сооружением), получаем
|
|
( V.1) |
Существенное влияние на размывы в нижнем бьефе имеет получающийся за водопропускным сооружением гидравлический прыжок, т. е. переход от глубины потока h ¢ < hк p к глубине h" > hк p.
При свободном истечении из отверстия (трубы или моста) в нижний бьеф поток, сжатый сооружением, веерообразно расширяется до бытовой ширины нижнего бьефа. Такое расширение сопровождается уменьшением глубины потока, резким возрастанием его скорости и переходом потока в бурное состояние (гидравлический водопад).
Значительное возрастание энергии в зоне гидравлического водопада вызывает появление прыжка воды при переходе от пониженных глубин (меньших критической) к бытовой глубине потока (большей критической глубины). Глубины h' и h" до прыжка и после него носят название взаимных или сопряженных глубин, а разность их h" - h' определяет собой высоту прыжка (см. рис. V.1).
Иногда при значительной разности в кинетической энергии до прыжка и за ним в потоке, помимо поверхностного, образуется донный валец (рис. V.2) и происходит, как говорят, разделение прыжка на два.
Последнее явление особенно нежелательно, так как в донном вальце происходит интенсивное гашение энергии, сопровождаемое усилением размывающей активности потока.
Разделение прыжка на два может образоваться в отогнанном прыжке; поэтому в гидротехнике всегда стремятся перевести прыжок из отогнанного в надвинутый или затопленный, которым присущ поверхностный режим и в которых не образуется донных вальцев.
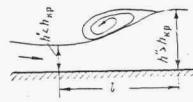
Рис. V . I . Прыжок воды с образованием поверхностного вальца

Рис. V .2. Прыжок воды с образованием поверхностного и донного вальцев
В зависимости от соотношения энергии потока на выходе из отверстия сооружения и в бытовом нижнем бьефе или в зависимости от соотношения глубин потока на выходе hвых. и его бытовой глубины hбыт истечение в нижний бьеф может происходить по трем характерным типам (рис. V.3).
Тип I - свободное истечение, когда глубина прыжка в сечении полного растекания больше бытовой глубины hбыт. При таком типе истечения переход к бытовой глубине происходит через отогнанный прыжок воды (рис. V.3, a).
По достижении берегов бытового русла, т. е. в сечении полного растекания, крайние струи потока отражаются от них (примерно под углом 20°), вследствие чего образуются небольшие симметричные гребни - косые прыжки, сходящиеся затем на динамической оси потока (рис. V.4). Это явление сопровождается небольшим всплеском воды. За сечением схода косых прыжков образуется прямой (отогнанный) прыжок, после чего поток приобретает характер медленно изменяющегося движения.
Как видно из рис. V.5, вблизи выходного отверстия сооружения образуются две зоны водоворотов, в которых уровень понижен, и обратные циркуляционные течения вызывают глубокие размывы.
Тип II - полусвободное истечение, когда глубина прыжка h" в сечении полного растекания меньше бытовой глубины hбыт, но возможная глубина прыжка на выходе h"вых больше глубины hбыт, т. е. когда справедливо неравенство
h" < hбыт < h"вых или 1,25 hКр > hбыт > h".
При таком типе истечения прыжок приближается к выходному отверстию сооружения, затопляя собой сначала сечение схода косых прыжков, а затем сечение полного растекания. Это будет крайний случай полусвободного истечения с полным растеканием, при котором образуется надвинутый прыжок (см. рис. V.3,6).
Если глубина отводящего русла больше глубины прямого прыжка, поток приобретает тенденцию к расширению в какую-нибудь одну сторону (сваливанию), в результате чего его активная ширина Bак в прыжке и до него становится меньше бытовой ширины потока bп, а скорости в активной струе резко возрастают (рис. V.6).
При сваливании потока в сторону (рис. V.7) он прижимается к берегу, что угрожает подмывом этого берега как вследствие повышенных скоростей в свальной струе, так и вследствие динамического удара масс воды о берег.
В этом случае длина прыжка значительно возрастает.
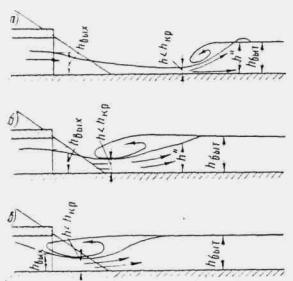
Рис. V .3. Истечение в нижний бьеф
Рис. V .4. Схема пространственного свободного растекания:
а -при раструбном выходном оголовке; б - при портальном оголовке
Тип III - несвободное истечение, когда глубина прыжка в сечении непосредственно за выходом из отверстия сооружения равна или менее бытовой глубины потока, т. е. когда
hбыт > 1,25 hкр, или hвых < hбыт.
При таком типе истечения прыжок затопляется полностью и надвигается на выходное отверстие сооружения (см. рис. V.3, в).
Рис. V .5. Схема растекания потока в нижнем бьефе
Узкая активная струя потока, прокладывая себе путь в массе воды затопленного прыжка, получает тенденцию к произвольному изменению своего направления. Образуется волнистое, так называемое сбойное течение (см. рис. V.7), начинающееся непосредственно за выходным отверстием.
Узкая активная струя при сбойном течении обладает большими скоростями и соответственно большой эрозионной способностью, так как энергия потока не расходуется на расширение и его активная зона несет в себе всю избыточную кинетическую энергию, приобретенную потоком в сооружении.
В плане размыв обычно ограничивается характерной строфоидальной кривой и образует, таким образом, некую чашу или ложбину (см. рис. V.5). Наибольшая глубина строфоидальной чаши размыва определяется гидравлическими характеристиками потока и при прочих равных грунтовых условиях находится в прямой зависимости от его расхода.
Практика показала, что наиболее опасным для нижнего бьефа
водопропускных сооружений является сбойное течение, которое может
образовываться при - ![]() < 8, т. е. в узких и глубоких отводящих руслах ( b0 - отверстие
водопропускного сооружения, Вр - ширина нижнего бьефа см. на
рис. V.6).
< 8, т. е. в узких и глубоких отводящих руслах ( b0 - отверстие
водопропускного сооружения, Вр - ширина нижнего бьефа см. на
рис. V.6).
Если ![]() > 8, глубина воды и уклон дна в нижнем бьефе невелики,
сбойное течение, как правило, не образуется.
> 8, глубина воды и уклон дна в нижнем бьефе невелики,
сбойное течение, как правило, не образуется.
Сбойное течение не увеличивает глубины ямы размыва за укрепленным участком, но значительно увеличивает размеры ямы в плане, т. е. вызывает необходимость увеличения площади укрепления.
Исследования И.К. Поклонского показали, что существенное влияние на размыв в отводящем русле при свободном растекании потока оказывает тип выходного оголовка и угол расширения потока в пределах выходного оголовка. Рекомендуется применять портальный выходной оголовок с углом раструба не более 80 °. При спокойном протекании потока (полусвободное и несвободное истечение) тип выходного оголовка не влияет на глубину ямы размыва.
Рис. V .6. Сваливание потока в сторону
Рис. V .7. Сваливание потока в сторону с подмывом берега
РАСЧЕТЫ ПРИ СВОБОДНОМ ИСТЕЧЕНИИ В НЕРАЗМЫВАЕМОЕ РУСЛО
Для расчета нижнего бьефа должны быть известны:
а) расчетный расход потока Q paсч;
б) отверстие сооружения b (а для трубы дополнительно тип выходного оголовка);
в) глубины потока hKp и vвых при Q paсч;
г) скорости потока vкр и vвых при Q paсч
д) уклон нижнего бьефа i;
е) бытовая ширина потока в нижнем бьефе B при Q paсч;
ж) бытовая глубина потока в нижнем бьефе hбыт при Q paсч
Расчет ведется в следующем порядке.
1. Определяют длину участка полного растекания потока по выходе из сооружения l1 (рис. V.8):
а) для труб с раструбным выходным оголовком с углом отклонения крыла bог,. (см. рис. V.4, а), меньшим или равным 50 °, по формуле
|
|
( V.2) |
б) для моста или трубы с портальным выходным оголовком или раструбным оголовком с углом b большим 50°, по формуле
|
|
( V.3) |
2. Определяют коэффициент возрастания скорости в гидравлическом водопаде по формуле
|
|
( V.4) |
где t - параметр уравнения, равный hбыт
а - коэффициент запаса, равный 1,05 ч ¸ 1,10.
3. Определяют скорость течения в сечении полного растекания (в зоне отогнанного прыжка)
v2 = v vкр
4. Определяют глубину потока в сечении полного растекания
|
|
( V.5) |
5. Определяют длину участка схода косых прыжков
|
|
( V.6) |
где y- угол косины прыжков по рис. V.4, а.
Далее находят элементы всплеска за линией схода косых прыжков и прямого прыжка на переходе к бытовым глубинам, т. е. длины участков: отгона l3, прыжка l4, глубины h3 и скоростей течения v3 и v 4 (см. рис. V.8).
Рис. V .8. Профиль растекания потока в нижнем бьефе:
1 - линия прыжков; 2 - сечение полного растекания; 3 - сечение схода косых прыжков; 4 -отгон прыжка; 5 -сечение прыжка
6. Для получения всех этих величин исчисляют значения энергии потока в сечениях - на выходе, полного растекания и схода косых прыжков Эвых,. Э2 и Э3.
Энергию в выходном сечении определяют по формуле
|
|
( V.7) |
Энергия в сечении полного растекания
![]()
По известным Э2 и h2 находят возможную наибольшую сопряженную глубину в сечении полного растекания по формуле
|
|
( V.8) |
7. Находят значения Э3 путем подбора глубины на всплеске за сходом косых прыжков h:3, для чего решают уравнение
|
|
( V.9) |
где ![]() - потери на длине l2
- потери на длине l2
|
|
( V.10) |
здесь п - коэффициент шероховатости русла на участке l2;
![]() и
и ![]()
h3 и v3 в первом приближении принимаются по формулам:
|
|
( V.11) |
|
|
( V.12) |
Подбор рекомендуется вести в табличной форме (табл. V.1)
Таблица V.1
Подбор значений Э3 и h3
|
№ приближения |
Глубины в м |
|
Скорости в м/сек |
|
h f |
Э 3 |
|
Превышение Δ(гр. 12-гр. 10) |
||||
|
h 2 |
h 3 |
hср |
v2 |
v3 |
v ср |
|||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
8 |
9 |
10 |
11 |
12 |
13 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
и т. д. |
|
|
|
|
|
|
|
|
|
|
|
|
Расчет ведется до совпадения цифр в графах 10 и 12.
8. По известным значениям h3 и v3 находят наибольшую
сопряженную глубину прыжка в сечении сходов косых прыжков ![]() по формуле
по формуле
|
|
( V.13) |
В условиях данной задачи значения ![]() и
и ![]() должны быть во всяком
случае более бытовой глубины потока hбыт
должны быть во всяком
случае более бытовой глубины потока hбыт
9. Определяют угол наклона огибающей линии прыжков (см. рис. V.8) по формуле
tg c
|
|
( V.14) |
10. Определяют:
а) длину участка отгона прыжка за сечением схода косых прыжков
|
l 3 = ( |
( V.15) |
б) длину прямого прыжка (перехода к бытовому уровню)
|
lпр = 0,5[4,5 |
(V.16) |
Допускается определять длину прыжка lпр по упрощенной формуле проф. Шаумяна:
|
lпр = 4,3 |
( V.17) |
11. Находят наибольшие размывающие скорости в зонах прыжков (по которым следует назначать тип укрепления)
|
|
( V.18) |
Значения коэффициента апр и функции ![]() могут быть с
достаточной практической точностью приняты по табл. V.2.
могут быть с
достаточной практической точностью приняты по табл. V.2.
В данной задаче значение функции ![]() следует принпмать
равным 1,64, тогда
следует принпмать
равным 1,64, тогда
vразн = 1,64 v2
где v, - средняя скорость в зоне отогнанного прыжка
v2 = v vкр
Таблица V.2
Значения
коэффициента Кориолиса апр и функции ![]()
|
Характеристика прыжка |
а прыжка |
|
|
Отогнанный |
3,0 |
1,64 |
|
Надвинутый |
1,85 |
1,3 |
|
Затопленный |
1,33 |
1,1 |
Примечание. Значение коэффициента абыт в таблице принято равным 1,1.
РАСЧЕТЫ ПРИ ПОЛУСВОБОДНОМ И НЕСВОБОДНОМ ИСТЕЧЕНИИ В НЕРАЗМЫВАЕМОЕ РУСЛО
При значении ![]() < hбыт и hбыт <
< hбыт и hбыт < ![]() прыжок образуется между выходным отверстием сооружения и
сечением расширения; истечение в нижний бьеф происходит по типу II полусвободного истечения с
надвинутым прыжком.
прыжок образуется между выходным отверстием сооружения и
сечением расширения; истечение в нижний бьеф происходит по типу II полусвободного истечения с
надвинутым прыжком.
В таком случае гидравлические расчеты ведут в следующем порядке.
1. Вычисляют энергию потока в выходном сечении по формуле ( V.7).
2. Принимая во внимание, что сечение полного растекания в данном случае затоплено, глубину потока перед прыжком находят из выражения
|
|
( V.19) |
3. По известной hсж определяют ширину прыжка (которая меньше полной ширины нижнего бьефа В)
|
|
( V.20) |
В данном случае h" равна бытовой глубине в отводящем русле hбыт.
4. Определяют длину отгона прыжка от выходного отверстия сооружения 1п, для чего выполняют следующие вспомогательные вычисления:
а) вычисляют теоретическую длину полного растекания потока 11 по формулам ( V.2) или ( V.3), т. е.
![]() или
или ![]()
в зависимости от типа выходного отверстия сооружения;
б) по формуле ( V.4) подсчитывают значение коэффициента возрастания скорости v при ![]() ;
;
в) вычисляют возможную скорость в сечении полного растекания v2 и глубину, соответствующую этой скорости:
v2 = ν vкр
![]()
г) по формуле ( V.8) вычисляют возможную наибольшую сопряженную глубину прыжка в сечении полного растекания hz
д) определяют возможную наибольшую сопряженную глубину прыжка в выходном сечении (рис. V.9)
|
|
( V.21) |
По найденным значениям l1, ![]() и
и ![]() находят длину
отгона прыжка от выходного отверстия
находят длину
отгона прыжка от выходного отверстия
|
|
( V.22) |
5. Определяют длину, на которой активная струя потока расширяется до ширины Вс.
Рис V 9. Полусвободное истечение с надвинутым прыжком
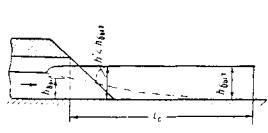
Рис. V .10. Несвободное истечение с полностью затопленным прыжком и сбойным течением
Для этого предварительно определяют ширину потока Вс, при которой не происходит общего размыва:
|
|
( V.23) |
Где
![]()
vдоп - допускаемая скорость на грунты или укрепление нижнего бьефа (по приложению 4).
Тогда длина расширения потока 1с находится по формуле
|
|
( V.24) |
где п - коэффициент шероховатости для укрепления нижнего бьефа (принимается по соответствующей таблице приложения 5);
bпр определяют по формуле ( V.20).
6. Вычисляют скорость течения в зоне прыжка
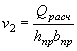
7. По известной v 2 и данным табл. V.2 находят значение размывающей скорости в зоне надвинутого прыжка по формуле ( V.18):
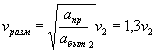
При hбыт > ![]() прыжок образуется вплотную у выходного отверстия
сооружения. Истечение происходит по типу III - несвободное с полностью затопленным прыжком и сбойным
течением в нижнем бьефе (рис. V.10).
прыжок образуется вплотную у выходного отверстия
сооружения. Истечение происходит по типу III - несвободное с полностью затопленным прыжком и сбойным
течением в нижнем бьефе (рис. V.10).
1. В данном случае глубину потока перед прыжком определяют, как обычно, по формуле hеж = 0,9 hкр, а ширину активной струи по формуле
|
|
( V.25) |
2. По известной bакт определяют длину расширения активной струи при сбойном течении
|
|
( V.26) |
Вследствие малого значения bакт длина растекания получается значительной.
3. Далее по известным геометрическим параметрам потока вычисляют среднюю скорость течения в зоне прыжка и подобно предыдущему - размывающую скорость в зоне затопленного прыжка по табл. V.2 и формуле ( V.18):
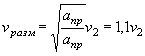
После окончательного выбора типа укрепления может появиться надобность в уточнении некоторых результатов расчетов в связи с изменением значения коэффициента шероховатости п, соответствующего окончательно выбранному типу укрепления.
РАСЧЕТЫ РАЗМЫВОВ ЗА УКРЕПЛЕНИЯМИ
Для назначения толщины рисбермы, заглубления предохранительного откоса в конце укрепления и выявления других исходных данных проектирования укрепления отводящего русла необходимо определить размеры возможных размывов.
При проектировании укреплений за малыми мостами, прямоугольными трубами и короткими безнапорными круглыми трубами можно пользоваться для определения глубины размывов упрощенными расчетными формулами канд. техн. наук О. В. Андреева (короткими трубами можно условно считать трубы, длина которых L < 15 d).
Как указывалось выше, размывы нижнего бьефа возникают вследствие превышения допускаемой скорости, а также ввиду развития донного вальца, причем чаще всего наибольшие размывы происходят именно в результате воздействия донных вальцов.
Однако необходимо учитывать, что вследствие растекания потока по укреплению с максимальными уклонами скорость потока значительно увеличивается и поэтому величины размывов, образующихся в результате превышения допускаемой скорости, также могут быть значительными, а в отдельных случаях даже превышать значения размывов, получающихся от воздействия донного вальца и определяемых по формуле
|
|
( V.27) |
где b0 - отверстие моста или трубы.
Остальные обозначения показаны на рис. V.11.
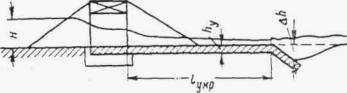
Рис. V .11. Схема размеров укреплений за сооружениями
В общем виде формула ( V.27) выглядит так:
|
|
( V.28) |
Таблица V.3
Определение глубины размыва
|
|
|
Fr 9 0 |
|
|
Fr 90 |
|
0 |
1,55 |
0,054 |
6 |
0,50 |
0,004 |
|
1 |
0,98 |
0,068 |
7 |
0,47 |
0,004 |
|
2 |
0,78 |
0,01 |
8 |
0,45 |
0,003 |
|
3 |
0,65 |
0,008 |
9 |
0,42 |
0,003 |
|
4 |
0,59 |
0,006 |
10 |
0,40 |
0,003 |
|
5 |
0,54 |
0,005 |
- |
- |
- |
Если, например, у моста отверстием b0 = 2 м предусмотрена длина укрепления lукр = 6 м, а подпор Н = 3 м, глубина размыва будет определена по отношению
![]()
откуда из табл. V.3
![]()
Тогда
![]() = 0,65 Н =
0,65-3 = 1,95 м.
= 0,65 Н =
0,65-3 = 1,95 м.
Расчет размывов вследствие превышения допускаемой скорости производится по формуле
|
|
( V.29) |
где Н - глубина воды перед сооружением;
b0 - отверстие сооружения;
lукр - длина укрепления;
![]() - допускаемая
скорость воды по грунту отводящего русла;
- допускаемая
скорость воды по грунту отводящего русла;
![]() -
параметр кинетичности потока, характеризующий сопротивляемость грунта размыву;
-
параметр кинетичности потока, характеризующий сопротивляемость грунта размыву;
![]() ) - безразмерная функция параметра кинетичности,
значения которой приведены в табл. V.4.
) - безразмерная функция параметра кинетичности,
значения которой приведены в табл. V.4.
Таблица V.4
|
|
0 |
0,001 |
0,005 |
0,01 |
0,05 |
0,10 |
0,20 |
0,30 |
0,40 |
0,50 |
0.60 |
|
|
∞ |
13,10 |
5,72 |
3,95 |
1,57 |
1,01 |
0,61 |
0,44 |
0,33 |
0,26 |
0,21 |
Так как все конструктивные расчеты
нижнего бьефа должны производиться по наибольшему из размывов, определенному по
формулам ( V.27) или ( V.28) и ( V.29), следует сразу выяснить, какой вид
размыва (от развития вальцов или от превышения допускаемой скорости) более
опасен. Для этого следует сопоставить два числа Фруда (параметра кинетичности),
вычисленные по фактической скорости на выходе из сооружения ![]() и по
допускаемой скорости с учетом длины укрепления Fr до.
и по
допускаемой скорости с учетом длины укрепления Fr до.
Размыв от превышения допускаемой скорости будет больше лишь в том случае, если число Фруда, определенное по фактической скорости, меньше, чем вычисленное по допускаемой скорости и длине укрепления. Числа Фруда, при которых размывы от обеих причин равны ( Fr до), приведены во второй строке табл. V.3.
Необходимо иметь в виду, что приведенные выше формулы ( V.27), ( V.28) и ( V.29), а также табл. V.3 и V.4 составлены для случаев свободного растекания, которое характеризуется следующими соотношениями (рис. V.12).
Ширина потока на расстоянии l от выходного сечения В = b0 + 2 l, глубина потока в сечении шириной В устанавливается
![]()
Рис. V .12. Свободное растекание потока
Если угол растекания (при наличии выходного оголовка) меньше угла свободного растекания, то в указанные выше формулы и таблицы следует вместо lукр вводить величину lукр. tga.
Длину укрепления целесообразно назначать по соотношению lукр = (3 ¸4) b0.
Для решения вопроса о необходимости укрепления отводящего русла следует пользоваться зависимостью между глубиной воды перед сооружением Н и наибольшим допускаемым размывом при отсутствии укрепления Δ hдоп
Н < Δ hдоп.
Во всех случаях Δ hдоп. не должна превышать глубины заложения фундамента.
В тех случаях, когда необходимо проектировать укрепления в иных условиях, чем те, при которых действительны упрощенные формулы, следует пользоваться приведенными ниже более общими расчетными формулами О. В. Андреева.
Этими формулами необходимо пользоваться при расчете элементов нижнего бьефа длинных безнапорных круглых труб ( L > 15 d), а также полунапорных и напорных труб:
|
|
( V.30) |
где Q - расчетный или наибольший расход (при расчете на наибольший расход Qмакс допускаемая скорость vдоп увеличивается на 20 % для мостов и на 35 % для труб);
bпр - ширина потока в прыжке: в случае свободного истечения и отогнанного прыжка bпр = В; в случае определения размыва непосредственно за выходным отверстием сооружения bnp = b0; при сбойном течении ширина прыжка определяется по формуле
![]()
![]()
vдоп - допускаемая скорость по мощению или грунту (может приниматься по приложению 4 или, более точно, определяться по формуле Д. И. Кумина):
|
vдоп = 39,2 d0,3 h0,2 |
( V.31) |
где
d - диаметр отдельных фракций в см;
h - глубина потока в см.
Зная действительную скорость на укрепленном участке и подставляя ее в формулу ( V.31), можно определить необходимый, диаметр камня d.
Глубина размыва по прыжку в зоне самого прыжка определяется по эмпирической формуле
|
Δ hпр = 1,85 h́́́́ ²пр - hбыт |
( V.32) |
где h́́́́ ²пр - наибольшая сопряженная глубина прыжка в сечении, определяемая по формуле
|
|
( V.33) |
Характер затухания размыва по прыжку изображен на графике (рис. V.13) для шероховатых и гладких русл.
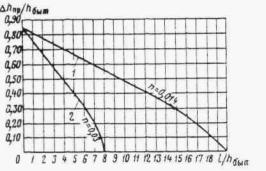
Рис. V .13. Характер затухания размыва по прыжку:
1 - за гладким руслом (бетоном); 2 - за шероховатым руслом (мощение)
Из графика видно, что кривая размывов при шероховатых руслах затухает скорее, чем при гладких, и что всякий размыв прекращается для шероховатых русел при l = 8 hбыт и для гладких при l = 20 hбыт.
График составлен в безразмерных характеристиках ![]() (ось абсцисс) и
(ось абсцисс) и ![]() (ось ординат), где hбыт - бытовая глубина в отводящем
русле.
(ось ординат), где hбыт - бытовая глубина в отводящем
русле.
Для получения истинной величины Δ hпр
найденное значение ![]() требуется умножить на
hбыт
требуется умножить на
hбыт
Пользуясь графиком, можно по заданному расстоянию / вычислить глубину ожидаемого размыва Δ hпр или задаваясь глубиной размыва Δ hпр, определить расстояние l.
Расчет размывов выполняют в следующем порядке:
1) вычисляют возможную наибольшую сопряженную глубину прыжка в рассматриваемом сечении h ²пр по формуле ( V.8):
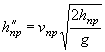
2) определяют глубину размыва по прыжку Δ hпр по формуле ( V.32):
Δ hпр = 1,85 h" - hбыт;
3) вычисляют ширину активной струи потока в рассматриваемом сечении bакт по формуле ( V.25):
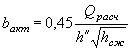
4) определяют глубину размыва по скорости Δ hс по формуле ( V.30) при vдоп:
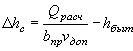
За расчетную глубину размыва принимается большая из двух: Δ hпр или Δ hc.
Можно, не производя расчетов по формулам, определять расчетный случай из рассмотрения выражения
|
|
( V.34) |
Если правая часть выражения окажется более глубины потока в рассматриваемом сечении, то за расчетный случай принимается размыв по прыжку, и расчет может быть ограничен решением уравнения ( V.32).
Если ![]() , то за расчетный случай принимается размыв по
скорости, и расчет может быть ограничен решением уравнения ( V.30).
, то за расчетный случай принимается размыв по
скорости, и расчет может быть ограничен решением уравнения ( V.30).
РАСЧЕТЫ РАЗМЫВА ПРИ СЛИВЕ С УСТУПА
Если при выходе из сооружения струя потока падает (сливается) с уступа (рис. V.14), что бывает в особых конструкциях нижнего бьефа, расчеты ведут в следующем порядке:
1) определяют глубину струи на гребне порога (при h0 > h Kp)
|
hп = 0,75 hк p |
(V.35) |
где hк p принимают из основного расчета сооружения.
При h0 > hк p следует принимать hп = h0;
2) определяют скорость течения на гребне порога
![]()
где ![]() - ширина
порога;
- ширина
порога;
3) определяют дальность полета струи
|
|
( V.36) |
где р - высота порога;
4) определяют скорость в слившейся струе на уровне низа порога
|
|
( V.37) |
5) определяют глубину слившейся струи
![]()
где ![]() - ширина нижнего
бьефа в месте падения струи (в призматическом русле постоянной ширины bсл = bп);
- ширина нижнего
бьефа в месте падения струи (в призматическом русле постоянной ширины bсл = bп);
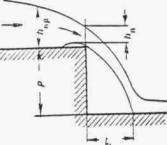
Рис. V .14. Слив потока с уступа
6) определяют тангенс угла падения струи
|
|
( V.38) |
7) определяют глубину размыва, соответствующую энергии падающей струи,
|
|
( V.39) |
где К - эмпирический коэффициент размыва, зависящий от угла падения и принимаемый по табл. V.5.
Таблица V.5
Значения коэффициента размыва К
|
Грунты |
Угол, образуемый падающей струей к горизонту, y в град. |
|||||
|
0 |
12 |
25 |
40 |
60 |
90 |
|
|
Обычные и скальные после длительного размыва |
1,4 |
1,7 |
2,0 |
2,4 |
2,7 |
3,3 |
|
Очень слабые (плывуны) |
1,4 |
1,8 |
2,4 |
2,8 |
3,3 |
4,5 |
Остальные обозначения прежние. Укрепление нижнего бьефа следует проектировать по v сл
Конструктивные расчеты
Конструктивные расчеты нижнего бьефа состоят из:
а) расчета длины укрепленного участка;
б) расчета ширины укрепления;
в) расчета толщины каменной рисбермы;
г) подбора шероховатости русла (выбора типа укрепления);
д) расчета глубины заделки укрепления (мощения) в его нижнем конце;
е) определения размеров отдельных камней укрепления (или размеров плиток).
Для конструкций нижнего бьефа со сливной стенкой, кроме того, должна быть установлена оптимальная высота порога.
Всякая конструкция нижнего бьефа преследует две цели:
а) предохранить русло за искусственным сооружением от размыва;
б) снизить (погасить) по возможности избыточную кинетическую энергию потока, выходящего из отверстия искусственного сооружения.
Первая цель достигается устройством достаточно устойчивого укрепления поверхности русла; вторая - приданием этому укреплению или особых форм, или повышенной шероховатости, способствующих гашению кинетической энергии.
Наиболее широко применяется плоское прямоугольное русло, укрепленное мощением или бетонной одеждой (рис. V.15).
Укреплению нижнего бьефа угрожает разрушение не только за счет значительной скорости потока, но и за счет восходящих течений, возникающих в бурном пульсирующем потоке, растекающемся за сооружением
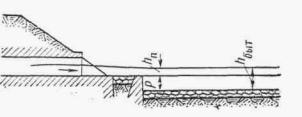
Рис. V .15. Укрепление нижнего бьефа
Рис. V .16. Схема растекания потока за сооружением
Укрепление в плане должно обеспечить растекание потока в пределах укрепленного русла с тем, чтобы не образовались размывы с боков.
По известному углу раструба растекающегося потока b (рис. V. 16) назначается конфигурация укрепления в плане. Между крайними струями и откосом насыпи возникают вихревые зоны, ввиду чего подошва откоса и откос на некоторую высоту должны быть также укреплены.
Плоское укрепление отводящих русел должно заканчиваться предохранительным откосом, заложенным ниже дна возможного размыва (рис. V.17). По условиям производства работ, как правило, применяются погребенные откосы с уклоном 1:1,5 (рис. V.18, а), хотя с точки зрения возникновения в этом месте размывов такие откосы создают так называемый донный режим, более опасный, чем поверхностный, при наличии на конце крепления вертикального зуба (рис. V.18, б).
Д. И. Кумин рекомендует применять концевое крепление в виде сочетания прямоугольной шпоры и гибкого тюфяка (рис. V.19).
Рис V .17. Схема предохранительного откоса
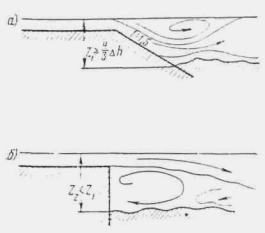
Рис. V .18. Схема течений за укреплением:
а - донный режим; б- поверхностный режим
Рис. V .19. Концевое крепление
Толщина укрепления у выходного оголовка S (см. рис. V. 1/) может быть определена по формуле
|
S » 0,35H |
(V.40) |
где Н - подпор перед сооружением.
Крупность камня в рисберме можно определить по формуле
![]()
где d - диаметр камня в м ;
![]() - скорость в м/с e к (
- скорость в м/с e к ( ![]() = 1,5
= 1,5 ![]() ),
),
или по формуле Кумина ( V.31) и формуле Н. Н. Беляшевского
|
d = (0,025 4 ¸ 0,030) vдоп2 |
( V.41) |
Толщина укрепления за рисбермой hконстр (см.рис. V.17) принимается в зависимости от типа укрепления по конструктивным соображениям (например, плиты толщиной 10 см на щебеночной подготовке 10 см).
Толщину погребенного откоса d из элементов, не скрепленных между собой, нужно принимать не менее 15 см, а для гибких тюфяков и плит, связанных между собой, она может быть и меньше.
Отводящие русла можно укреплять каменным мощением разных видов, рисбермами, каменными набросками и другими давно известными способами.
Для предотвращения вредного воздействия свального течения нижнему бьефу может быть придана особая конфигурация так называемого веерного водослива (рис. V.20), способствующая равномерному и симметричному растеканию потока. Веерный водослив укрепляют мощением.
В некоторых случаях может оказаться целесообразным придавать укреплению нижнего бьефа форму строфоидальной чаши, соответствующую форме естественного размыва русла. Укрепленный таким образом нижний бьеф изображен на рис. V.21.
Может применяться также тип нижнего бьефа с высоким порогом (стенкой падения или сливной стенкой), устраиваемым непосредственно за выходом потока из отверстия сооружений для затопления отогнанного прыжка (см. рис. V.15).
Гидравлические расчеты конструкции нижнего бьефа обычного типа (плоского, прямоугольного) заключаются в следующем.
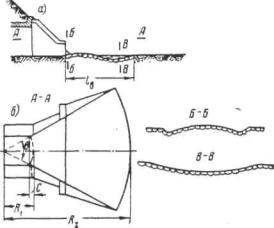
Рис. V .20. Веерный водослив
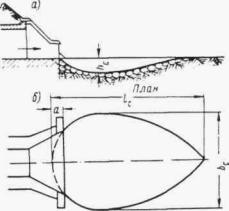
Рис. V .21. Укрепление в виде строфоидальной чаши
Рис. V .22. Длина укрепления нижнего бьефа
1. По скорости течения подбирают тип одежды (приложение 4) и соответствующий этому типу коэффициент шероховатости п. Значения коэффициента п можно принимать по таблице приложения 5.
2. Подбирают толщину рисбермы и толщину погребенного откоса d.
В общем случае полная длина укрепления
нижнего бьефа слагается из пяти участков (рис. V.22):
1) участка полного растекания потока l1;
2) участка схода косых прыжков l2;
3) отгона прыжка l3;
4) длины прыжка l4 (или lпр);
5) конструктивного запаса от прыжка до кромки укрепления l5. Длина l5 зависит от типа укрепления. В укреплении с погребенным откосом, в котором можно допустить сгон прыжка в размыв, l5. можно принимать равным нулю ( l5. = 0).
При истечении в нижний бьеф по I типу (свободное истечение) длина укрепления составляется из всех пяти участков
L = l1 + l2+ l3 + l4 + l5
При истечении по II типу (полусвободное истечение)
L = l3 + l4 + l5,
где l3 = lп. - по формуле ( V.22), а l4 = 1С - по формуле ( V.24).
При истечении по III типу (несвободное истечение)
L = l4 + l5
Здесь l4 = lс вычисляется по формуле ( V.24).
При пользовании формулой для L необходимо иметь в виду, что в качестве варианта для технико-экономического сравнения следует подбирать повышенную шероховатость или укреплять только зону прыжка, прибавляя конструктивный запас l5, за которым согласно графику (см. рис. V.13) глубина размыва для сооружения будет безопасной, ввиду чего далее русло укреплять не требуется.
Подбирая тип повышенной шероховатости, не следует упускать из виду двух обстоятельств:
во-первых, эффект, обусловливаемый повышением донной шероховатости, не распространяется на весь поток, если последний имеет достаточную глубину (1 м и более). Если в придонном слое скорости вследствие повышения шероховатости дна падают, то у поверхности они одновременно возрастают;
во-вторых, применение в равнинных условиях сложных типов гасителей (гребенки, шашки, зубья, планки, ряжи, водобойные стенки и т. п.) не может быть рекомендовано, так как все они требуют постоянного надзора и ухода и при их заносе (заилении) или обледенении перестают работать.
Конструкции гасителей должны быть просты и надежны. С этой точки зрения наиболее приемлемым типом повышенной шероховатости для равнинных сооружений будет мощение крупным булыжником ( dкамня > 30 см), рваным камнем, мощение « с изюмом», или так называемые чешуйчатые рисбермы, а также укрепление бетонными блоками.
Ширина укрепления определяется из условия, что размыв происходит по площади, ограниченной строфоидой. Продольная ось строфоиды lcтр (вдоль потока) по условию затухания размыва в укрепленном русле по графику (см. рис. V. 13) имеет длину lcтр = 18 Δh.
Тогда ширина строфоиды Bстр определяется по формуле
|
Bстр = 0,671 lстр = 12Δ h |
( V.42) |
Последним элементом расчета нижнего бьефа является определение размеров отдельных камней мощения ( по формуле Кумина, Беляшевского или Андреева).
К конструкции нижнего бьефа по рис. V.14 расчетом должна быть определена оптимальная высота стенки.
Этот расчет производится из условий равенства глубин в бытовом русле hбыт и за порогом hп + р (см. рис. V.14), т. е. hбыт = hп + р. Отсюда высота стенки
р = hбыт - hп,
где hп - глубина воды на пороге шириной bп,
|
|
( V.43) |
bn - ширина потока на пороге;
h" - возможная наибольшая сопряженная глубина прыжка на пороге,
![]()
где v2 = vn.
Уравнение решается методом подбора.
Расчеты размыва за порогом выполняются по указаниям стр. 71.
В 1964-1965 гг. в ЦНИИСе канд. техн. наук Л. Г. Бегамом и В. С. Муромовым выполнена работа по расчету косогорных труб, где также рассмотрены вопросы расчетов нижнего бьефа за косогорными трубами со специальными гасителями энергии (см. главу VI).
ГЛАВА VI
РАСЧЕТЫ КОСОГОРНЫХ СООРУЖЕНИЙ
ОБЩИЕ ПОЛОЖЕНИЯ
К косогорным сооружениям относятся мосты и трубы, располагаемые на косогорных ходах железнодорожных линий (при поперечных уклонах местности в пределах искусственного сооружения 0,02 и круче), а также подводящие и отводящие русла и обустройства к этим сооружениям.
В косогорных сооружениях, как правило, формируется бурный поток. Бурный режим протекания воды по косогорам и связанные с этим повышенная активность и эрозионная деятельность потока заставляют предусматривать варианты сооружений с большими отверстиями, позволяющими ограничиться более простыми конструкциями искусственного русла и косогорных устройств.
Ввиду этого трубы на косогорах нужно рассчитывать только по безнапорному режиму при Q pасч; (для уменьшения напряженности их работы). При ступенчатом расположении звеньев трубы необходимо учитывать при расчете отверстия его уменьшение по высоте за счет перепадов. Гидравлические расчеты косогорных сооружений должны вестись аналогично с расчетами отверстий малых искусственных сооружений, т. е. по двум расходам: Q pасч и vдоп Q m а kc и 1,35 vдоп на железных дорогах общего пользования и расчетному расходу Q pасч и vдоп на автомобильных и железных дорогах промышленных предприятий.
Возвышение высшей точки внутренней поверхности косогорных труб над поверхностью воды в трубе при расчетном расходе должно быть не менее, чем это установлено для равнинных труб (см. табл. II.3).
Однако в косогорных трубах вследствие высокой кинетической энергии потока и значительных углов сужения подводящего русла на входном участке получается высокий взлет струй, необходимый зазор между уровнем воды и верхом трубы не обеспечивается и поэтому расход vдоп должен отличаться от расчетного расхода для равнинных труб Q pасч
Согласно лабораторным опытам, выполненным в 1964-1965 гг. ЦНИИСом (канд. техн. наук Л. Г. Бегамом и В. С. Муромовым), допустимые расходы для косогорных прямоугольных труб должны определяться по формуле
|
Qдоп = kQ pасч |
( VI.1) |
где k - коэффициент, зависящий от угла сужения q рис. VI. 1) и от числа Фруда перед сооружением. Число Фруда определяется по формуле
|
|
( VI.2) |
где v -средняя скорость в м/сек,
h - средняя глубина в м;
b - ширина быстротока по дну в м;
Q - расход воды в м3/сек;
g - ускорение силы тяжести в м/сек2.
Ниже приведена таблица для определения коэффициента ![]() в прямоугольных
трубах (при q
= 20°).
в прямоугольных
трубах (при q
= 20°).
Таблица VI.1
Значения
коэффициента ![]()
|
Число Фруда Fr |
Прямоугольный быстроток шириной, вдвое большей отверстия трубы |
Трапецеидальный быстроток, шириной по дну, вдвое большей отверстия трубы |
||||||||||
|
Нормальное входное звено |
Повышенное входное звено |
Нормальное входное звено |
Повышенное входное звено |
|||||||||
|
Отверстие |
||||||||||||
|
1,5 |
2,0 |
2,5 |
1,5 |
2,0 |
2,5 |
1,5 |
2,0 |
2,5 |
1,5 |
2,0 |
2,5 |
|
|
8 |
1,0 |
1,0 |
1,0 |
1,34 |
1,34 |
1,35 |
- |
- |
- |
- |
- |
- |
|
10 |
1,0 |
1,0 |
1,0 |
1,34 |
1,34 |
1,35 |
1,0 |
1,0 |
1,0 |
1,25 |
1,25 |
1,26 |
|
12 |
1,0 |
1,0 |
1,0 |
1,33 |
1,34 |
1,35 |
0,98 |
0,98 |
0,98 |
1,26 |
1,26 |
1,27 |
|
14 |
1,0 |
1,0 |
1,0 |
1,32 |
1,33 |
1,34 |
0,95 |
0,95 |
0,95 |
1,24 |
1,25 |
1,26 |
|
16 |
1,0 |
1,0 |
0,99 |
1,32 |
1,32 |
1,32 |
0,90 |
0,90 |
0,89 |
1,20 |
1,20 |
1,20 |
|
18 |
0,98 |
0,98 |
0,97 |
1,31 |
1,30 |
1,29 |
0,89 |
0,89 |
0,86 |
1,16 |
1,15 |
1,14 |
|
20 |
0,96 |
0.96 |
0,96 |
1,27 |
1,26 |
1,24 |
0,94 |
0,94 |
0,94 |
1,15 |
1,14 |
1,13 |
|
22 |
0,94 |
0,92 |
0,90 |
1,24 |
1,20 |
1,17 |
1,00 |
1,00 |
0,98 |
1,13 |
1,10 |
1,07 |
|
24 |
0,90 |
0,80 |
0,83 |
1,18 |
1,14 |
1,10 |
1,06 |
1,04 |
0,98 |
1,12 |
1,08 |
1,05 |
|
25 |
0,90 |
0,85 |
0,80 |
1,16 |
1,10 |
1,05 |
1.08 |
1,01 |
0,96 |
1,11 |
1,06 |
1,00 |
Величины коэффициента k в графах 2-8 и 11 приведены по опытным данным ЦНИИСа, а в графах 9. 10 и 12, 13 - по интерполяции.
Сопряжение прямоугольных и трапецеидальных быстротоков с круглыми трубами целесообразно осуществлять применительно к схемам, разработанным и испытанным в 1964-1965 гг. в ЦНИИСе (рис. VI.2, VI.3 и VI.4).
При испытаниях установлено также, что коническое звено на входе в круглую трубу для пропуска расчетного расхода при бурном режиме улучшает характер протекания потока в трубе и увеличивает запас пропускной способности (наибольшая глубина на входе оказывается на 20- 30 % меньше, чем при нормальном входном звене).
Иногда целесообразно лоток сооружения устраивать в виде быстротока с уклоном, соответствующим уклону местности; гашение энергии в этом случае производится в конце сооружения. Иногда, наоборот, гашение энергии производится на протяжении всего сооружения путем устройства перепадов или серий водобойных колодцев.
Очень эффективным и экономически целесообразным приемом гашения энергии во многих случаях оказывается устройство так называемой искусственной шероховатости русла (при условии обеспечения надзора и ухода за таким руслом).
Однако основным типом косогорных сооружений на периодически действующих водотоках следует считать быстротоки, в которых обеспечивается свободный транзит наносов и постоянный режим потока. Водобойные колодцы резко нарушают режим водотока, что является их недостатком.
Рис. VI .1. Входной быстроток и труба:
1 - быстроток; 2 - труба
Расположенные на косогорах мосты имеют некоторые преимущества перед трубами: мосты меньше изменяют бытовые условия протекания потока, русло под мостом легче осматривать и ремонтировать.
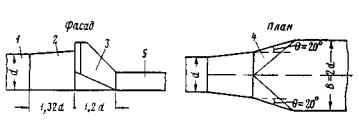
Рис. VI .2. Сопряжение прямоугольного быстротока шириной В = 2d с круглой трубой:
1 -труба; 2 - коническое входное звено; 3 - сужение; 4 - примазка; 5 - входной быстроток
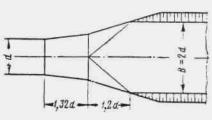
Рис. VI .3. Сопряжение трапецеидального быстротока шириной В = 2d с круглой трубой
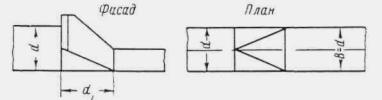
Рис. VI .4. Сопряжение прямоугольного быстротока шириной В = d с круглой трубой
Как правило, в условиях косогорной местности на железных дорогах устраивают комплекс косогорных сооружений, состоящий из:
а) подводящего русла, представляющего собой быстроток прямоугольного или трапецеидального поперечного сечения. Быстротоки сооружаются
с уклонами, большими критических, и могут иметь для гашения энергии водного потока на входе или выходе водобойные колодцы или водобойные стенки, а также по всей длине быстротока - искусственную шероховатость;
б) собственно искусственного сооружения (моста или трубы). Косогорную трубу обычно укладывают с перепадами, устраиваемыми или на каждом звене, или в конце секций, состоящих из нескольких звеньев; кроме того, для гашения энергии потока в трубе может быть устроена искусственная шероховатость;
в) выходных устройств, к которым относится гаситель энергии на выходе и укрепление отводного русла (нижнего бьефа).
Ниже приведены гидравлические расчеты всех указанных элементов комплекса косогорных сооружений.
* Глава дополнена с использованием работы ЦНИИСа «Методические указания по гидравлическому расчету косогорных труб» (канд. техн. наук Л. Г. Бегам и В. С. Муромов) и проектного задания унифицированных косогорных водопропускных труб (Ленгипротрансмост).
БЫСТРОТОКИ
Основным типом косогорных сооружений следует считать быстротоки, которые в сочетании с искусственной шероховатостью, гашением энергии водного потока водобойным сооружением, располагаемым в начале или в конце быстротока, а также при учете аэрации потока, могут сооружаться с очень крутыми уклонами.
Явление аэрации водного потока возникает при значительных скоростях воды в быстротоках и заключается в насыщении воды пузырьками воздуха, вследствие чего поток испытывает некоторое дополнительное торможение, учитываемое увеличением коэффициента шероховатости
|
nаэр = an |
(VI.3) |
По данным А. А. Ничипоровича, коэффициент а можно принимать по табл. VI.2 в зависимости от уклона быстротока i и гидравлического радиуса R.
Таблица VI.2
Значения коэффициента аэрации а
|
Гидравлический радиус R |
Уклон быстротока i |
||
|
0,1 ¸ 0,2 |
0,2 ¸ 0,4 |
Больше 0,4 |
|
|
0,1 ¸ 0,3 |
1,33 |
1,33 |
2,0 |
|
Меньше 0,1 |
1,33 |
2,0 |
3,3 |
При скоростях течения воды v < 20 м/сек глубину аэрированного потока следует принимать по формуле
|
|
( VI.4) |
где h - расчетная глубина неаэрированного потока;
v - средняя скорость течения в м/сек.
Необходимо отметить, что последние исследования в СССР и за рубежом показали, что аэрация оказывает сильное влияние на гашение энергии потока, однако количественная сторона этого явления изучена недостаточно, приведенные в табл. VI.2 величины коэффициента аэрации а изменяются скачкообразно, что, конечно, явно не соответствует действительному состоянию аэрированного потока. Безусловно, явление аэрации подлежит дальнейшему изучению.
Быстротоки могут быть призматические и непризматические. Призматические быстротоки представляют собой естественные или искусственные русла или лотки постоянного сечения (а также водопропускные трубы), уклоны которых больше критического.
Искусственные быстротоки могут сооружаться железобетонными, бетонными или каменными и служить как для подведения воды к водопропускному сооружению в косогорных условиях, так и для отведения из водоотводных канав или водопропускных сооружений.
Непризматические (трапецеидальные в плане) (см. рис. VI. 1 и VI.5) быстротоки также могут быть железобетонными, бетонными и каменными; устраиваются они в качестве переходных участков, при помощи которых поток сужается перед входом в сооружение или расширяется по выходе из него.
Рис. VI .5. Трапецеидальный быстроток
РАСЧЕТ БЫСТРОТОКОВ
При проектировании быстротоков должен быть произведен расчет:
а) ширины быстротока и глубины наполнения при равномерном режиме (в достаточно длинных быстротоках);
б) кривой свободной поверхности на участке от h Kp до h0;
в) подходного участка быстротока;
г) выходного участка быстротока (воронки);
д) гасителя энергии на выходе из быстротока.
Основные виды продольного профиля призматических быстротоков приведены на рис. VI.6 (пунктиром показана линия критических глубин потока с равномерным движением):
А при i1 > iкр ( h1 < hкр); i2 = iкр ( h0 = hкр)
Б при i1 > iкр ( h01 < hкр).
Здесь возможны три случая:
1) h02 > h01 - нормальная глубина II участка является взаимной (сопряженной) глубиной по отношению к нормальной глубине I участка. Прыжок возникает на переломе уклонов; выше и ниже прыжка движение равномерное (рис. VI.7);
2) h02 > h́01 - нормальная глубина II участка больше взаимной глубины первого участка; в этом случае прыжок возникает на I участке (рис. VI.8);
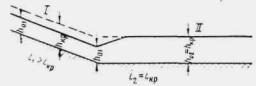
Рис. VI .6. Профиль потока в призматическом быстротоке
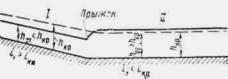
VI .7. Прыжок на переломе уклонов
3) h02 < h́01 - нормальная глубина второго участка меньше взаимной глубины первого участка; прыжок в этом случае возникает на втором участке (рис. VI.9).
В. При i2> i1> iKp на обоих участках возникает кривая спада (рис. VI.10).
Глубину в конце быстротока можно определить, построив кривую свободной поверхности на быстротоке.
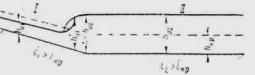
Рис. VI .8. Прыжок на первом участке
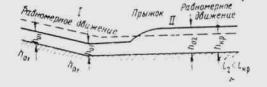
Рис. VI .9. Прыжок на втором участке
Если длина быстротока равна или больше длины кривой спада или подпора, то глубина в конце быстротока равна нормальной глубине h0. Если же, наоборот, длина кривой спада или подпора будет больше длины быстротока, глубина в конце быстротока определится по уравнению неравномерного движения.
На рис. VI.11 показан случай, когда длина быстротока L менее длины спада l( L < l спада), а расчетная глубина в конце быстротока hpacч > h0.
Для прямоугольных бетонированных русел длину L1, на которой устанавливается равномерный режим, т. е. положение, когда L = l спада, можно определять по графику приложения 10. В большинстве случаев длины призматических русел бывают достаточными, чтобы на них успевал устанавливаться равномерный режим и отвечающая ему глубина потока h0.
Порядок расчета быстротока, разработанный Союздорпроектом (Альбом типовых проектов сооружений на автомобильных дорогах, вып. 15), следующий.
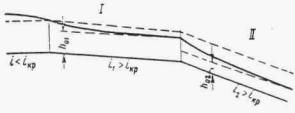
Рис. VI .10. Кривая спада
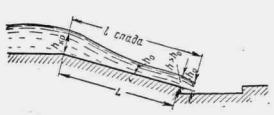
Рис. VI .11. Быстроток, длина которого меньше длины спада
Для прямоугольных бетонированных русел длину L1, на которой устанавливается равномерный режим, т. е. положение, когда L = l спада, можно определять по графику приложения 10. В большинстве случаев длины призматических русел бывают достаточными, чтобы на них успевал устанавливаться равномерный режим и отвечающая ему глубина потока h0.
Порядок расчета быстротока, разработанный Союздорпроектом (Альбом типовых проектов сооружений на автомобильных дорогах, вып. 15), следующий.
1. По формуле проф. Ю. Н. Даденкова определяют наивыгоднейшую ширину быстротока по дну
|
b =
0,765 |
( VI.5) |
2. В первом приближении назначают глубину воды в быстротоке (в условиях равномерного течения воды) h0, по которой определяют w0, c0 и R0.
Для данного быстротока определяют по приложению 5 коэффициент шероховатости n а затем по формуле ( VI.3) п aэр. Имея значения R0 и nаэр, по приложению 6 или 7 определяют значение С0:
![]()
Если v0< vдоп, можно увеличить i0; затем проверяют, соответствует ли Q0 = w0 v0 расчетному расходу Qрасч и при совпадении их (с точностью до 10 %) глубину h0 принимают к расчету.
3. По графику приложения 8 или по формуле 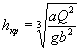 определяют
значение hк p.
определяют
значение hк p.
4. Определяют длину кривой спада lсп по приложению 10 или по упрощенной формуле проф. В.И. Чарномского:
|
|
( VI.6) |
где Э0 и Экр - удельные энергии сечения потока:
![]()
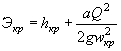
i0 - заданный уклон.
Определяют ![]() по формуле
по формуле
|
|
( VI. 7) |
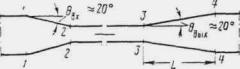
Рис. VI .12. Подводящий и отводящий быстротоки
5. Сравнивают длину быстротока L с l спада и если L>1 спада, то в конце быстротока устанавливается глубина h0. При L < l спада глубину следует определять по методу акад. Н. Н. Павловского подбором значений глубин в диапазоне между h0 и h Kp; та глубина, для которой отрезок кривой спада будет равен длине быстротока L, и будет искомой глубиной в конце быстротока.
Быстроточные русла, подводящие воду к сооружению (трубе), обычно сужаются, а отводящие от него воду - расширяются (рис. VI.12).
Сжатие потока может производиться под разным углом сужения, однако для обеспечения плавности вписывания потока и во избежание образования ударов и прыжков (как показали лабораторные опыты и практика) этот угол следует назначать не более 20°.
Расчеты сужающихся русел по уравнению Чарномского следует выполнять с разбивкой сужающегося участка на несколько отрезков, решая это уравнение для сечений по концам таких отрезков.
При расчете сужающегося русла необходимо иметь в виду, что наибольшие скорости в конце участка сужения могут образоваться и при расходах, меньших расчетного ( Q < Q pacч)
Поэтому уклон сужающегося участка следует назначать по наиболее неблагоприятному случаю, а также проверять образование прыжка воды на входе в сооружение при Q pacч
Расширяющиеся участки быстротоков должны проектироваться с углами роспуска q, которые во избежание отрыва потока от боковых стенок и для равномерного заполнения русла потоком без резкого изменения глубин в сечении следует определять по формуле
|
|
( VI.8) |
где h и v принимаются для входного сечения 3-3 (см. рис. VI.12) расширяющегося участка.
Если по формуле получается q > 20 °, его нужно принимать равным 20 °.
При наличии в конце расширяющейся воронки водобойной стенки (а также в трапецеидальных расширяющихся колодцах) угол может быть увеличен до 30 °. На расширяющемся участке, имеющем тот же уклон, что и на остальных участках быстротока, образуется плавная вогнутая кривая спада.
Общая длина расширяющегося участка обычно диктуется местными условиями или экономическими соображениями и, таким образом, к началу расчета бывает известна. Гидравлические характеристики потока во входном сечении расширяющегося участка ( h и v) также бывают известны.
Таким образом, расчет расширяющегося участка сводится к определению глубины потока и его скорости в конце участка. Эти расчеты могут быть выполнены при помощи уравнения Чарномского путем подбора в отношении определяемой глубины потока или по графикам (рис. VI.13- VI.16).
Решая уравнение Чарномского для расширяющегося русла, следует иметь в виду, что достаточно произвести расчеты для крайних сечений 3-3 и 4-4 (см. рис. VI.12).
Расчет следует начинать с входного сечения, для которого известны hп„ и vп, принимаемые равными
hп = h0; vп = v0.
Помимо расширяющихся участков, перед вводом потока в основные гасительные сооружения в конце каждого быстротока рекомендуется устраивать горизонтальный или с небольшим уклоном расширяющийся участок - воронку, на протяжении которой будет происходить предварительное гашение энергии потока (рис. VI.17).
Если воронку устраивают с горизонтальным или имеющим малый уклон дном, бывает целесообразно назначать длину воронки lвор по длине совершенного прыжка, определяемой по графикам (рис. VI.18 и VI.19).
Если длина воронки lвор диктуется конструктивными и экономическими соображениями по желаемой ширине основных гасительных сооружений, то она определяется по формуле
|
|
( VI.9) |
где q - угол роспуска воронки.
Применение искусственной шероховатости не исключает необходимости учета влияния аэрации.
Русла, запроектированные в виде ступенчатых перепадов, в которых длина каждой ступени оказывается недостаточной для гашения на ней энергии потока, также относятся к быстротокам. В этом случае ступени перепадов рассматриваются как элементы искусственно повышенной шероховатости, а все русло в целом - как быстроток, коэффициент шероховатости для которого п0 становится больше его обычных величин. Указания к определению значений п0 для таких быстротоков приводятся ниже.
На рис. VI.13 - VI.16 приведены графики, предназначенные для графоаналитического расчета воронок с малыми углами роспуска ( q = 6°30' и 8°), устраиваемых в конце быстротечных русел.
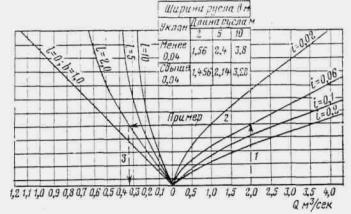
Рис. VI .13. График зависимости уклона i и глубины h м от расхода Q м3/сек и ширины b м
в расширяющихся бетонированных быстротоках шириной 1 м
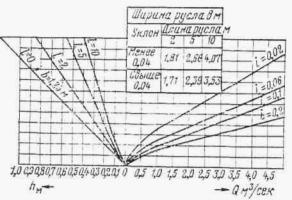
Рис. VI .14. График зависимости уклона i и глубины h м от расхода Q м3/сек и ширины b м
в расширяющихся быстротоках шириной 1,25 м
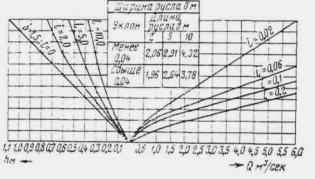
Рис. VI .15. График зависимости уклона i и глубины h . м от расхода Q м3/сек и ширины b м
в расширяющихся бетонированных быстротоках шириной 1,5 м
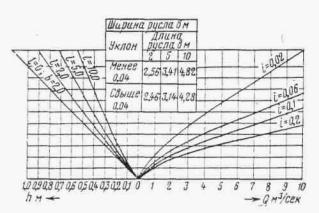
Рис. VI .16. График зависимости уклона i и глубины h м от расхода Q м3/сек и ширины b м
в расширяющихся бетонированных быстротоках шириной 2 м
Графики разработаны для русел шириной b = 1; 1,25; 1,5 и 2 м.
По указанным графикам в зависимости от заданного расхода, уклона на воронке i и ее длины lвор можно найти глубину потока в конце воронки и по этой глубине определить скорость на выходе из воронки по формуле
![]()
Рис. VI .17. Выходной быстроток-воронка
На графиках приведена вспомогательная табличка, по которой определяется ширина русла в конце воронки по ее длине и углу роспуска.
Пользование графиками пояснено примером на рис. VI.13, где пунктирными линиями указан порядок построения.
Для суждения о длине l, на которой происходит расширение русла до желаемой величины, служит график, показанный на рис. VI.18. График составлен исходя из ширины русла 1 м. При иной ширине русла длина l, получаемая из графика, пропорционально увеличивается. Так, например, длина воронки расширения русла шириной 2 м при кратности расширения k = 3 и угле роспуска русла q = 15 ° будет
l =3,8·2 =7,6 м (k = b1/b)
Длина горизонтальной воронки расширения lвор в конце быстротока, исчисляемая из условия образования на ней прямого совершенного прыжка, в зависимости от уклона подводящего русла i и удельного расхода потока q при угле роспуска воронки q = 15° может быть получена из графика рис. VI. 19.
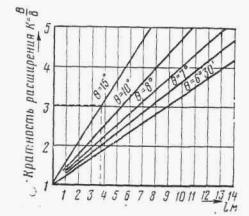
Рис. VI .18. График зависимости длины расширяющегося быстротока
от угла роспуска воронки q (при ширине русла 1 м)
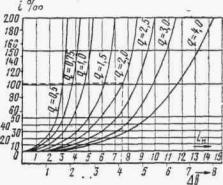
Рис. VI . 19. График для определения размеров воронки
(длины l в конце быстротока в зависимости от q и i )
Из графика может быть получено также уширение русла Δ b, получающееся на данной длине воронки (см. пример на рис. VI.19).
ИСКУССТВЕННАЯ ШЕРОХОВАТОСТЬ
Искусственная шероховатость может применяться при условии регулярного ее осмотра и очистки на периодически действующих водотоках. В трубах рекомендуется применять искусственную шероховатость для отверстий не менее 1,25 м.
Кроме указанных ниже типов искусственной шероховатости, в трубах может производиться искусственное увеличение шероховатости до п = 0,020 путем мощения лотков рваным камнем на цементном растворе (рис. VI.20).
Проектируя искусственную шероховатость, следует иметь в виду, что она вызывает увеличение глубин в потоке. Следовательно, в трубах с искусственной шероховатостью необходимо дополнительно проверять соблюдение требований табл. II.3 о просвете между потолком трубы и свободной поверхностью воды в ней.
Искусственная шероховатость бывает двух основных видов - донная и бортовая. Наибольшее распространение получила донная шероховатость.
Рекомендуемые конструктивные типы искусственной шероховатости для косогорных сооружений приведены в приложении 29.

Рис. VI .20, Мощение лотков труб рваным камнем
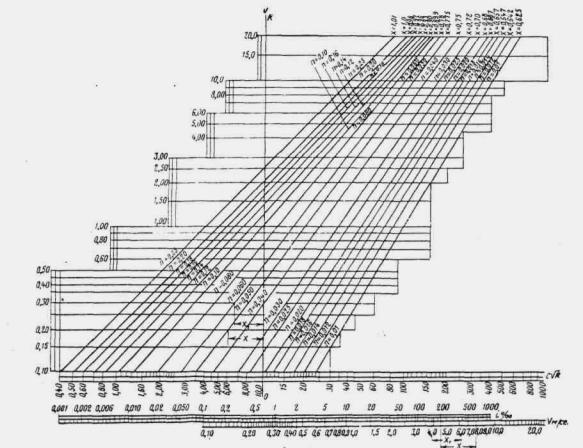
Рис. VI .21. Номограмма инж. И. И. Херхеулидзе для определения v
по известным R , п и i или п по известным v , R и i
Скорость воды в быстротоке с искусственной шероховатостью можно определить по формуле Шези:
|
|
( VI.10) |
где n0 - коэффициент донной усиленной шероховатости, определяемый для каждого типа искусственной шероховатости (см. приложение 29);
R - гидравлический радиус, определяемый с учетом уменьшения глубины живого сечения h на высоту ребер а, т. е. h́' = h - а при донной шероховатости, и уменьшения ширины живого сечения b на две толщины бортовых ребер, т. е. b' = b - 2 а'. Обычно донная шероховатость применяется в прямоугольных широких лотках, в узких же трапецеидальных лотках применяется комбинированная шероховатость.
Гидравлический расчет искусственной шероховатости заключается в подборе ее типа.
По известным Q, i, b и vдоп определяется глубина потока h, затем R и
![]() а
а
Пользуясь номограммой И.И. Херхеулидзе (рис. VI.21), можно быстро по известным vдоп, R и i определить n'0
Пример 1. Дано R = 0,2 м; i = 200‰; п = 0,050.
Порядок определения v по графику: на горизонтальной линии, соответствующей R = 0,20, определяют расстояние X (от 0 до пересечения с наклонной, соответствующей n = 0,050); далее расстояние X откладывают вправо на шкале уклонов от точки i = 200‰; на нижней шкале v определяют v = 8 м/сек.
Пример 2. Дано: R = 0,3 м; i = 150‰; п = 0,06.
Определяем по нижней шкале v = 6,1 м/сек.
По эмпирическим формулам Е. А. Замарина вычисляют значения п0 для нескольких типов искусственной шероховатости, в случае необходимости вносят поправки на аэрацию и эти значения n'0 сравнивают с п0.
Выбирается тот тип искусственной шероховатости, для которого п0 » n'0.
КОСОГОРНАЯ ТРУБА
На косогорах часто целесообразно укладывать звенья (или секции) труб горизонтально, следуя уклону местности с помощью вертикальных уступов (ступеней) в стыках звеньев (рис. VI.22). Эти уступы (ступени) гидравлически действуют, как повышенная шероховатость.
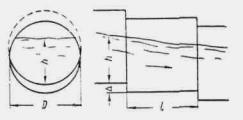
Рис. VI .22. Круглая ступенчатая труба
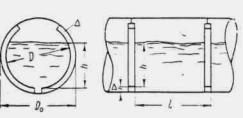
Рис. VI .23. Круглая труба с поперечными ребрами
Повышенная шероховатость достигается в трубах путем
устройства поперечных ребер (рис. VI.23), причем ее следует учитывать при относительном шаге
шероховатости ![]() < 25. При
< 25. При ![]() > 25 влиянием
повышенной шероховатости можно пренебречь.
> 25 влиянием
повышенной шероховатости можно пренебречь.
Коэффициент Шези для прямоугольных труб, уложенных со ступенями, определяют по формуле
|
|
( VI.11) |
при горизонтальных звеньях
|
|
( VI.12) |
Для круглых труб при ступенчатой укладке звеньев коэффициент Шези определяют следующим образом:
а) определяют модуль расхода при заполнении трубы наполовину
|
|
( VI.13) |
где ![]() - коэффициент Шези
без повышенной шероховатости
- коэффициент Шези
без повышенной шероховатости ![]() ;
;
б) вычисляют коэффициент шероховатости n0,5
при h ³ 0,225 D
|
|
( VI.14) |
при h0,5< 0,225 D
|
|
( VI.15) |
где n0,5 вычисляют по формуле ( VI. 14);
в) вычисляют коэффициент Шези по формуле
|
|
( VI.16) |
где R - гидравлический радиус живого сечения трубы при данной глубине воды.
Коэффициент Шези круглых труб с повышенной шероховатостью (рис. VI.23) определяют следующим образом:
а) вычисляют модуль расхода при заполнении трубы наполовину:
|
|
( VI.17) |
где D0 - полный диаметр трубы: i - уклон трубы;
б) если l = (0,8 ¸ 1,2) D0, находят максимальный для данных ребер коэффициент шероховатости
|
|
( VI.18) |
и вычисляют соответствующий коэффициент Шези
|
|
( VI.19) |
где R - гидравлический радиус живого сечения потока в створе ребра, где диаметр в свету
D= D0 - 2Δ.
В случае заполнения трубы h < 0,225 D следует пользоваться формулой
|
|
( VI.20) |
в) если ![]() - менее 0,8 или более 1,2, то вычисляют величину
- менее 0,8 или более 1,2, то вычисляют величину
|
|
( VI.21) |
где e = 2,718
Искомый коэффициент шероховатости
|
п = n2м См - ( n2 - n2м См) x, |
( VI.22) |
где См - коэффициент Шези по Маннннгу;
пм - коэффициент шероховатости по Маннингу;
п0 - коэффициент шероховатости, вычисленный при I - D0 по формуле ( VI.18) или ( VI.20).
Исследования круглых труб с повышенной шероховатостью, произведенные в гидравлической лаборатории НИИЖТа канд. техн. наук И.К. Поклонским, позволили сделать вывод, что степень сжатия потока
![]()
где D0 - внутренний диаметр трубы в свету;
D - диаметр трубы в сечении, где расположены ребра, т. е.
D = D0 - 2Δ;
Δ - высота ребра.
ВЫХОДНЫЕ УСТРОЙСТВА
На выходе из косогорного сооружения (особенно, трубы), как правило, устраиваются гасители энергии, а отводное русло на некоторой длине укрепляется.
В любом случае расчетом должно быть определено плановое очертание отводного русла, длина и глубина концевого устройства - зуба или погребенного откоса.
Глубину и скорость потока при повышенной шероховатости на выходе из труб с постоянным уклоном можно определять по формуле Шези, если их длина превышает 20 м, а при отсутствии повышенной шероховатости - при длине труб свыше 30 м.
При наличии в трубе участков с различными уклонами глубина и скорость на выходе определяются расчетом неравномерного движения потока (так же, как и для быстротоков).
ГАСИТЕЛЬ КОНСТРУКЦИИ ЦНИИСа
Для уменьшения скорости потока на выходе из сооружения могут применяться гасители с двумя водобойными порогами конструкции ЦНИИСа (рис. VI.24), с одной водобойной стенкой конструкции Ленгипротрансмоста, а также расширяющиеся водобойные колодцы (рис. VI.25).
Гаситель конструкции ЦНИИСа рекомендуется располагать на участках с уклонами не более 0,2. Расчет этого гасителя при уклоне его дна i < 0,05 производится следующим образом.
В начале раструба гасителя принимают глубину воды hсж - сжатая глубина потока на выходе из трубы.
Высоту первого водобойного порога принимают в пределах
|
C 1 = (l,2 ¸ l,5)hcж . |
(VI.23) |
Определяют глубину воды в начале раструба:
при ![]() по формуле
по формуле
|
|
( VI.24) |
при ![]() по формуле
по формуле
|
|
( VI.25) |
где 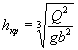 -критическая глубина.
-критическая глубина.
По глубине ![]() проверяют соблюдение
в выходном участке трубы необходимого просвета над поверхностью потока. Для
этого строят кривую подпора от начала раструба вверх по течению.
проверяют соблюдение
в выходном участке трубы необходимого просвета над поверхностью потока. Для
этого строят кривую подпора от начала раструба вверх по течению.
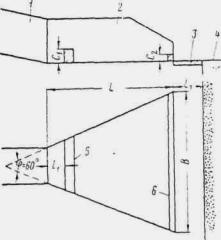
Рис. VI .24. Схема гасителя ЦНИИСа:
1 - труба; 2 - раструб; 3 - крепление; 4 - отводное русло; 5 - 1-й водобойный
порог; 6 - 2-й водобойный порог
Рис. VI .25. Расширяющийся водобойный колодец:
1 - водобойная стена; 2 - валец
Если просвет окажется недостаточным, то следует предусмотреть выходное повышенное звено или уменьшить величину С1.
Расстояние до первого водобойного порога определяют по формуле
|
l1 = (0,55 ¸ 0,70) b. |
( VI.26) |
Длина раструба
L = 11 + S,
где S - дальность падения струи,
|
|
( VI.27) |
Fr - число Фруда, определяемое по формуле ( VI.2).
Ширина раструба в конце
|
B = b + 1,15L. |
( VI.28) |
Высота второго водобойного порога
|
С2 = (0,25 ¸ 0,30) hсж. |
( VI.29) |
Продольный профиль потока в гасителе строится следующим образом.
Глубина потока t в плоскости напорной грани первой водобойной стенки определяется по одной из следующих формул:
При ![]()
|
|
( VI.30) |
при ![]()
|
|
( VI.31) |
Глубина воды hрасч в начале раструба определяется по формулам ( VI .24) и( VI.25).
Наибольшая высота подъема струй в раструбе
|
|
( VI.32) |
Горизонтальное расстояние до места наибольшего подъема струй
|
|
( VI.33) |
где ![]()
а = hm - t.
Уравнение поверхности потока в осевой вертикальной плоскости
|
h = Ах 2 + Ex + t, |
( VI.34) |
где ![]() ,
, ![]()
h - высота воды потока на расстоянии х от напорной грани первой водобойной стенки, отсчитываемая от основания ее напорной грани.
Длина раструба при его уклоне более 0,05:
|
|
( VI.35) |
При угле раструбности j = 60° очертание боковых струй в проекции на вертикальную плоскость, проходящую по оси сооружения, определяется по формулам:
|
|
|
|
h = 3,07 A x 2 +1,75 Ex + t |
( VI.36) |
To же, в плоскости стен, ограничивающих раструб
|
h = 2,3 Ах 2 + 1,51 Ex + t |
( VI.37) |
В тех случаях, когда по конфигурации лога невозможно разместить нормальный гаситель с углом раструбности j = 60 °, принимают угол j ³ 30 °, боковые стенки в плане делаются прямолинейными.
Все гидравлические расчеты при j ≠ 60 ° производятся так же, как и для j = 60 °, за исключением определения траекторий струй.
Траектория крайних струй в проекции на плоскость симметрии
|
|
( VI.38) |
Траектория крайних струй в плоскости боковых стен
|
|
( VI.39) |
Здесь А, Е и t имеют те же значения, что и в формулах ( VI.27) ( VI.30), ( VI .31) и ( VI.34).
Пример расчета гасителя конструкции ЦНИИСа (рис. VI.26). Дано: Q = 9,45 м3/сек; i = 0,15. Труба прямоугольная b = 1,5 м, высота звеньев 2 м, hсж =0,76 м.
Решение. Скорость потока в конце трубы
![]()
Число Фруда
![]()
Высота первой водобойной стенки
С1= 1,3 hсж = 1,3·0,76 ≈ 1 м
Расстояние до первой стенки
l1 = 0,63 b = 0,63·1,5≈1 м.
Критическая глубина
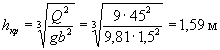
Рис. VI .26. К примеру расчета гасителя ЦНИИСа:
1 - два нормальных звена; 2 - валец; 3 - просвет 30 см; 4 - косогор; 5 - открытый
участок; 6 - боковые стены; 7 - стенка конструктивной высоты; 8 - крайние струи;
9 - средняя струя; 10 - линия падения струй
Дальность падения средней струи
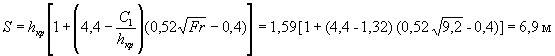
Высота второй водобойной стенки
С2 = 0,275 hсж =0,275·0,76 » 0,20 м.
Глубина в начале раструба
![]() м.
м.
Глубина в плоскости напорной грани первой водобойной стенки
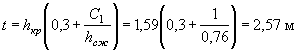
Наибольшая высота подъема струй
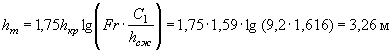 ;
;
a = hm - t = 3,26 - 2,57 = 0,69 м ;
![]()
![]()
![]()
Положение максимальной высоты средней струп
![]()
Уравнение поверхности средней струи
h = Ах2 + Ех + t = - 0,146 х2 + 0,634 х + 2,57.
Таблица VI.3
Координаты средней струи
|
х |
х2 |
Ах2 |
Eх |
h |
х |
х2 |
Ах2 |
Eх |
h |
|
0 |
0 |
0 |
0 |
2,57 |
5 |
25 |
-3,65 |
3.17 |
2,09 |
|
2,17 |
4,7 |
-0,637 |
1,374 |
3,22 |
6 |
36 |
-5,25 |
3,80 |
1,12 |
|
3 |
9 |
-1,315 |
1,900 |
3,16 |
6,9 |
47,6 |
-6,95 |
4,37 |
0,11 |
|
4 |
16 |
-2,34 |
2,64 |
2,87 |
8,0 |
64 |
-9,25 |
5,08 |
-1,60 |
Таблица V1.4
Координаты крайних струй в проекции на осевую плоскость
|
х |
x3 |
3,07А х2 |
1,75 Eх |
h |
х |
x3 |
3,07А х2 |
1,75 Eх |
h |
|
0 |
0 |
0 |
0 |
2,57 |
3 |
9 |
- 4,16 |
3,32 |
1,64 |
|
1,3 |
1,69 |
-0,76 |
1,44 |
2,25 |
4 |
16 |
- 7,18 |
4,62 |
0 |
|
2,17 |
4,7 |
-2,11 |
2,40 |
2,86 |
5 |
25 |
- 11,2 |
5,55 |
-3,08 |
По значениям х и h из табл. VI.3 и VI.4 построена траектория струй (см. рис. VI.26) и намечено очертание боковых стен гасителя, а также определены размеры раструба в плане.
Глубина воды в начале раструба hрасч = 2,47 м сравнивается с сопряженной глубиной бурного потока в трубе, определяемой по формуле
h"сж =
0,5 hсж
( ![]() = 0,5-0,76 (
= 0,5-0,76 ( ![]() ) = 3,24 м;
) = 3,24 м;
так как h"сж > hрасч, имеем обычный случай, когда гидравлический прыжок располагается в раструбе.
Далее определяют положение вальца в трубе
jх = 0,550 + 0,0304 Fr - 0,300 ![]() = 0,550 + 0,0304·9·2 - 0,300
= 0,550 + 0,0304·9·2 - 0,300 ![]() = 0,365
= 0,365
Глубина воды в 1 м от раструба
hрасч1.= hрасч - jΔ x - 2,47·0,365·1,0 = 2,10 м.
Уклон следующего участка
j2 = 0,550 + 0,0304·9,2 - 0,300 ![]() = 0,45;
= 0,45;
hрасч2.= hрасч1 - j2Δ x= 2·10 - 0,45·1,0 = 1,65 м
Аналогично
hрасч0 =1,65 - 0,52=1,13 м.
По этим данным на продольном разрезе трубы наложен продольный профиль вальца и установлено, что для обеспечения над потоком просвета 1/6 от высоты трубы необходимо непосредственно выше раструба устроить открытую вставку длиной 1 м, уложив два последних звена без уступа между ними; между последним звеном и открытой вставкой предусмотрен уступ двойной высоты, что обеспечивает в конце последнего звена просвет 0,3 м.
РАСШИРЯЮЩИЙСЯ КОЛОДЕЦ
Расчет расширяющегося водобойного колодца выполняется в следующем порядке.
1. Определяют дальность падения струи l1:
|
|
( VI.40) |
где ![]()
р - высота стенки падения;
h и v - глубина и средняя скорость перед стенкой падения;
b - угол наклона подводящего русла к горизонту.
Для ускорения расчета целесообразно пользоваться графиком рис. VI.27.
2. Подбором по приведенному ниже уравнению определяют сжатую глубину в месте падения струи
|
|
( VI.41) |
где' ![]() - полный напор в
конце быстротока
- полный напор в
конце быстротока ![]()
b - ширина колодца в месте падения струй.
3. Определяют взаимную (сопряженную) глубину h"сж, а также ширину колодца на выходе и длину L подбором по уравнению прыжковой функции для прямоугольного сечения:
|
|
( VI.42) |
где w1 - площадь сжатого сечения;
w2 - площадь сжатого сечения в конце колодца.
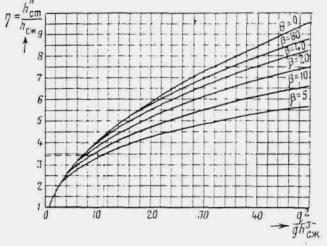
Рис. VI .27. График для определения глубины расширяющегося колодца
При этом принимается
|
В = b + 2 L tg j, |
( VI.43) |
где b - отверстие трубы или ширина быстротока в месте падения струи;
L - полная длина колодца,
|
L = 3,2 h"сж +a |
( VI.44) |
а - толщина водобойной стенки понизу.
4. Определяют высоту водобойной стенки с учетом удельного расхода в сечении потока у стенки:
|
С = s h"сж - H1 |
( VI.45) |
где s = 1,05 - коэффициент затопления прыжка;
Н1 - превышение уровня воды в колодце над верхом водобойной стенки,
![]()
![]() - средняя скорость подхода воды к стенке;
- средняя скорость подхода воды к стенке;
H = s h"сж - глубина воды перед стенкой;
qcт - удельный расход потока на стенке;
Н0 - полный напор над гребнем незатопленной водобойной стенки
|
|
( VI.46) |
m = 0,42
5. Определяют сжатую глубину за водобойной стенкой при условии Т0 = Н0 по формуле ( VI.41).
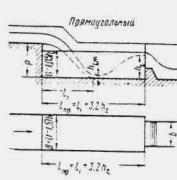
Рис. VI .28. Прямоугольный колодец
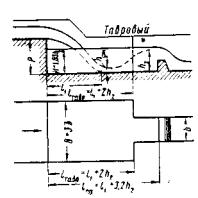
Рис. VI .29. Тавровый колодец
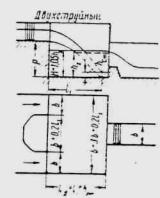
Рис. VI .30. Двухструйный колодец
6. Определяют дальность падения струи 11 переливающейся
через водобойную стенку по формуле ( VI.40), но при условии b
= 0 и ![]()
7. Определяют ширину потока у места падения струи, переливающейся через водобойную стенку:
|
bc = b + 2(L +l)tg j |
( VI.47) |
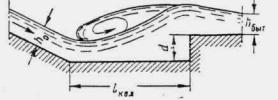
Рис. VI .31. Колодец без стенки падения
8. Определяют скорость в сжатом сечении за водобойной стенкой:
![]()
9. За водобойной стенкой русло укрепляется на ширине bст, длине l материалом, выдерживающим скорость vсж в сжатом сечении. Ниже приводятся гидравлические расчеты обычного прямоугольного водобойного колодца, водобойной стенки и комбинированного водобойного колодца.
Кроме расширяющихся колодцев наиболее часто применяются прямоугольные, (рис. VI.28), тавровые (рис. VI.29), двух cтруйные (рис. VI.30) и прямоугольные без стенки падения (рис. VI.31).
Тавровый колодец (см. рис. VI.29) имеет ширину входа большую, чем ширину выхода, вследствие чего полная длина таврового колодца меньше, чем прямоугольного.
Водобойные колодцы круглого или прямоугольного очертания с небольшими размерами в плане следует располагать у входа в косогорное сооружение в случаях, когда вода подводится с двух сторон нагорными канавами. В этом случае обе струи, сталкиваясь, падают почти вертикально и, ударяясь о водную подушку на дне колодца, теряют запас энергии.
Двухструйный колодец (см. рис. VI.30) имеет перед входом специальное устройство для разделения потока на две части. Каждая половина потока, падая вниз, отражается от противоположной стенки и ударяется в водную подушку с образованием подвернутого прыжка; после поворота в плане на 90 ° обе половины потока соударяются и теряют скорость.
В приложении 31 дана таблица основных размеров и гидравлических характеристик типовых водобойных колодцев, запроектированных Лентрансмостпроектом для удельных расходов q = 0,5 ¸ 3 м3/сек, высоты стенки падения p = 2 ¸ 5 м и скоростей подхода воды v = 2 ¸ 8 м/сек
РАСЧЕТ ВОДОБОЙНЫХ КОЛОДЦЕВ
Водобойные колодцы обеспечивают гашение энергии потока при выходе его в нижний бьеф с покрытой струей (надвинутым прыжком) (рис. VI.32).
Расчет водобойного колодца сводится к определению достаточной его длины и глубины.
Водобойные колодцы с пониженным дном обычно устраивают в конце быстротоков или иных косогорных сооружений. В начале сооружений применять подобные водобойные колодцы не следует ввиду отсутствия в них выхода для воды после прохода паводка.
Для того, чтобы в колодце обеспечивался надвинутый прыжок, его длина должна быть не менее суммы длин l1 (длины полета струи) и lпр (длины совершенного прыжка), т. е.
lкол = l1 + lпр
Величина 11 определяется по формуле
|
|
( VI.48) |
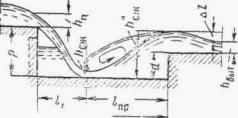
Рис. VI .32. Схема гашения энергии
Длину совершенного прыжка /пр можно принимать по формуле проф. Шаумяна:
|
lпр = 4,3 h"сж. |
( VI.49) |
Прыжок в колодце обычно подперт и имеет несколько меньшую длину, чем длина совершенного прыжка, составляя 0,7-0,8 этой последней, т. е.
l ́пр = (0,7 ¸ 0,8) lпр,
или
l ́пр = (0,7 ¸ 0,8) 4,3 h"сж,
в среднем
|
l ́пр = 3,2 h"сж, |
( VI.50) |
Тогда окончательно длина колодца 1кол определится по формуле
|
|
( VI.51) |
где 11 можно определять по графику рис. VI.33.
При устройстве колодца в конце быстротока стенка падения р отсутствует (см. рис. VI.31).
Следовательно, длина полета струи l1 = 0 и длина колодца приравнивается длине подпертого прыжка, т. е.
|
|
( VI.52) |
где ho и v0 - нормальная глубина и соответствующая ей скорость в конце быстротока.
Глубину колодца d определяют из условия получения в колодце надвинутого прыжка. Для этого она должна несколько превышать наибольшую сопряженную со сжатой глубину h"сж, Размер этого превышения обычно задается коэффициентом s = 1,05-1-1,10.
В общем виде глубина колодца получается из уравнения
|
d = s h"сж - ( hбыт + Δ z). |
( VI.53) |
Значение букв, входящих в уравнение, показано на рис. VI.32.
Ввиду того что по формуле ( VI.53) глубину колодца приходится находить методом подбора, решая несколько раз уравнение ( VI.53), удобнее ее определять по графику приложения 30. Применение колодцев, в которых h"сж ³ 2 hсж не допускается, так как при этом в примыкающем русле образуются стоячие волны, вызывающие значительные размывы.
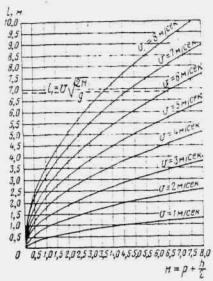
Рис. VI .33. График для определения дальности полета струи при уклоне подводящего русла i < 0,10.
Пример. Дано: Q = 6 м3/сек; v = 6 м/сек; i = 0,09; р = 6 м; b = 1 м.
Определяется глубина
![]()
тогда
![]() ;
;
по графику l1 = 6,9 м.
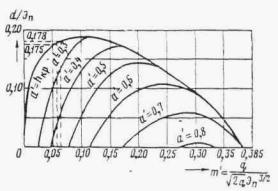
Рис. VI .34. График для определения глубины колодца d
Пример. Дано q = 3 м3/сек; v = 6 м/сек; h = 0,5 м; р = 2+0,6 = 2,6 м; (задавшись d = 0,6 м); подводящее русло прямоугольное; b = 1 м.
Определяем:
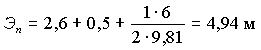
По рис. VI.
35 ![]() , т. е. т 1
= 0,021·3 = 0,063;
, т. е. т 1
= 0,021·3 = 0,063;
![]() , откуда d = 0, 88 м; во
втором приближении задается d
= 0,92 м;
, откуда d = 0, 88 м; во
втором приближении задается d
= 0,92 м;
![]()
По рис. VI.35
![]() ; т' = 0,057
; т' = 0,057
![]() ; d
= 0,175·5,26 = 0,92 м, т.
е. правильно.
; d
= 0,175·5,26 = 0,92 м, т.
е. правильно.
Для расчета водобойных колодцев рекомендуется пользоваться графоаналитическими методами, дающими достаточно точные результаты и значительно облегчающими подсчеты.
Расчет прямоугольного колодца заключается в следующем:
длина колодца lкол = l1 + lпр; дальность полета струи l1 может быть определена по графику на рис. VI.33, разработанному Лентрансмостпроектом;
длину подпертого прыжка определяют по формуле ( VI.50), в которой h"сж может быть найдена по графику, составленному Рахмановым (см. приложение 30).
По известным l1 и h"сж длина колодца lкол определяется по формуле ( VI.51).
Глубина водобойного колодца может быть подобрана при помощи графика, составленного канд. техн. наук В. В. Смысловым (рис. VI.34).
На этом графике нанесены кривые безразмерной величины а', т. е. отношения глубины в нижнем бьефе hбыт к энергии на пороге колодца Эп, исчисленной по формуле
|
|
(VI.54) |
т. е.
![]()
Огибающая кривая на графике отвечает случаю, когда безразмерная величина а' равна относительной критической глубине потока в нижнем бьефе, т. е.
![]()
По оси абсцисс на графике нанесены значения безразмерного параметра
|
|
( VI.55) |
Этот параметр представляет собой характеристику данного сопрягающего сооружения.
Кривые а' отсекают на оси абсцисс значения т', при которых сопряжения бьефов совершаются по типу надвинутого прыжка и, следовательно, при которых не требуется устройства колодца.
На оси ординат графика нанесены безразмерные величины
глубины колодца ![]()
Пользование графиком заключается в следующем.
По известным ЭП, d и q вычисляют а' и т' [по формуле ( VI.55)].
Проверяют по графику значение т', отсекаемое линией а'.
Если т' на графике окажется меньше исчисленного по формуле ( VI.55), это означает, что сопряжение бьефов совершается с отогнанным прыжком, для затопления которого требуется колодец.
Тогда, назначая примерную глубину колодца d, вычисляют новые
значения Эп, т', а (при p1 = р +
d) и, проводя из
точки пересечения ординаты нового значения т' с новой кривой а' горизонтальную прямую, читают на оси
ординат относительную глубину колодца ![]() . Истинное значение этой глубины oпределяется по формуле
. Истинное значение этой глубины oпределяется по формуле
d = а'Эп.
Если это значение будет равно или немного меньше принятого d, то на этом определение глубины колодца заканчивается.
Если d будет иное, то назначают новую глубину колодца dz по соотношению d1 < dz < d и проделывают те же действия до тех пор, пока между назначенной и полученной по графику глубиной не будет удовлетворительной сходимости.
Пример. Дано: q = 4 м3/сек, р = 3 м, v = 6 м/сек, h = 0,67 м, русло прямоугольное.
Определяется
![]()
По формуле
hк p = 0,482 ![]() ;
;
hк p = 1,21 м; ![]()
По графику
![]()
Отсюда
hсж = 0,385·1,21 =0,47 м; ![]() = 2,10·1,21 =2,54 м.
= 2,10·1,21 =2,54 м.
Для облегчения пользования графиком Смыслова на рис. VI.35 помещен вспомогательный
график, из которого при данной величине Эп находят отношение ![]() и определяют значение
m', отвечающее формуле ( VI.55).
и определяют значение
m', отвечающее формуле ( VI.55).
Расчет расширяющегося колодца производится в следующем порядке:
1) должны быть известны расчетный расход Q paсч, ширина подводящего русла b, уклон русла и бытовая глубина отводящего русла hбыт, высота падения струи р (назначается);
2) определяют ширину порога в точке А (см. рис. VI.25):
bп = b+2 b tgθ
3) находят критическую глубину в подводящем прямоугольном русле (на графике приложения 9);
4) подсчитывают глубину воды на пороге
hп = 0,75 hк p;
5) определяют подходную скорость
![]() .
.
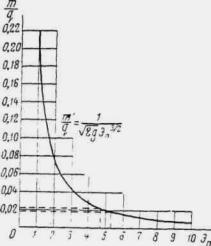
Рис. VI .35. График для определения глубины водобойного колодца d
(пунктиром показано решение примера к рис. VI .34)
6) по графику рис. VI.33 находят дальность полета струи 11 для чего
подсчитывают ![]()
7) находят скорость в сжатом сечении колодца
![]()
8) определяют глубину в сжатом сечении
![]()
где b' - ширина колодца в точке O;
9) по графику рис. VI.27 находят h"сж;
10) глубину колодца определяют по формуле
d = h"сж - hбыт
длину колодца - по формуле
lр кол = l1 + 4,5 h"сж
РАСЧЕТ ВОДОБОЙНОЙ СТЕНКИ
При наличии перед водобойной стенкой перепада (рис. VI.36), с которого сливается струя, образуется колодец, дно которого находится на уровне нижнего бьефа. Водобойные стенки могут устраиваться на подходе к искусственному сооружению при необходимости успокоить слишком бурное движение подходящего потока.
Гидравлический расчет водобойной стенки аналогичен расчету водобойного колодца и заключается в определении высоты стенки рст и в подборе расстояния от перепада до стенки l. Основным элементом этого расчета является определение такой высоты стенки рст, которая обеспечила бы сопряжение потока до и за стенкой по типу покрытой струи.
Исходя из этой предпосылки высота стенки рст в прямоугольном русле шириной b определяется по формулам:
|
pст = s h"сж - Hст |
( VI.5 6) |
|
|
( VI.5 7) |
|
|
( VI.5 8) |
|
|
( VI.5 9) |
Рис. VI .36. Колодец с водобойной стенкой
При m=
0,42 эта формула имеет вид ![]()
При устройстве семейства водобойных стенок расчет высоты каждой предыдущей стенки ведется в следующем порядке.
Назначают высоту стенки рст по схеме незатопленного водослива и после подбора высоты последующей стенки проверяют по схеме затопленного водослива. В этих расчетах за высоту падения рп для данной стенки принимают высоту предыдущей стенки рСт{ n-1).
Расстояние от перепада до стенки l (или между двумя стенками), необходимое для правильной работы стенок, определяют так же, как и длину водобойных колодцев по формуле ( VI.52).
При устройстве семейства водобойных стенок расстояние l между ними допускается определять по формуле
l = 4,5 h"сж
где h"сж определяется по формуле ( VI.58).
РАСЧЕТ КОМБИНИРОВАННОГО ВОДОБОЙНОГО КОЛОДЦА
При решении практических задач встречаются иногда случаи, когда отдельно взятый водобойный колодец получается чрезмерно глубоким, а также отдельно взятая водобойная стенка - чрезмерно высокой.
В таких случаях оказывается целесообразным устройство водобойного колодца комбинированного типа (рис. VI.37). Подобные колодцы во многих случаях оказываются наиболее экономичными.
Гидравлический расчет комбинированных водобойных колодцев исходит из предпосылки, что глубина колодца d - наименьшая возможная, а высота стенки р - наибольшая . возможная; этому условию отвечает критическая форма сопряжения. В таком случае расчет комбинированного водобойного колодца обычного прямоугольного сечения выполняется в следующем порядке. Рассчитывают глубину водобойного колодца d, как обычно, по формуле ( VI.53). Затем из условия затопления струи за колодцем подбирают высоту водобойной стенки по формуле
Рис. VI .37. Водобойный колодец комбинированного типа
|
рст = 0,9(Эн б - Hст) |
( VI.60) |
где Эн б - допустимый запас энергии в потоке относительно дна нижнего бьефа;
|
|
( VI.61) |
j - коэффициент скорости, равный 0,9;
h" - наибольшая сопряженная глубина с глубиной в нижнем бьефе hбыт.
|
|
( VI.62) |
Напор Н водобойной стенки Hст определяют по формуле ( VI.57).
Подставляя значения Энб и Нст в формулу ( VI.60), получают высоту водобойной стенки рст.
Далее уменьшают ранее исчисленную глубину водобойного колодца d на рст и получают общее соотношение в комбинированном сооружении.
Длина комбинированного водобойного колодца определяется обычным способом по уравнению
|
|
( VI.63) |
Полученные в результате расчета размеры колодца проверяются по указаниям главы V в отношении сопряжения потока за стенкой (расчеты размыва при сливе с уступа).
Сказанное выше в отношении водобойных колодцев о недопустимости соотношения h"сж ³ 2 hсж справедливо также и в отношении водобойных стенок. Для определения высоты водобойных стенок могут быть использованы графики проф. Чертоусова, составленные им для прямоугольного русла (рис. VI.38 и VI.39).
Водобойные стенки могут работать или как незатопленный водослив, когда вода свободно сливается с них в нижний бьеф, т. е. когда высота стенки равна или более глубины в нижнем бьефе, или как затопленный водослив, когда горизонт нижнего бьефа затапливает стенку. Методы расчета тех и других стенок различны. Графики Чертоусова отвечают обоим случаям.
График рис. VI.38
составлен для незатопленной стенки. По оси ординат на графике нанесены значения
отношения ![]() , в котором Эп определяется по уравнению
, в котором Эп определяется по уравнению
![]() .
.
По оси абсцисс отложена функция этого отношения, равная
|
|
( VI.64) |
где pст - высота стенки.
Для стенок прямоугольного или трапецеидального профиля можно принимать: при а = 1,0 k = 0,706; при а = 1,1 k = 0,729.
Пользование графиком сводится к следующему: .
1) вычисляют Эп по формуле ( VI.54);
р - высота порога падения перед стенкой;
j - в зависимости от местных условий равно 0,80-1,0 (в среднем 0,9 при отсутствии особых соображений);
Рис. VI .38. График для определения высоты незатопленных водобойных стенок
при прямоугольном сечении отводящего русла.
Пример. Дано: q - 4 м3/сек; d = 1 .м; К = 0,706; р = 3,67 м; v = 6 м/сек ΄ j = 0,90.
Определяем:
![]()
По графику приложения 9:
![]()
h = 2,20; ![]()
откуда
Рст = 0,94
2) вычисляют
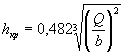
3) вычисляют отношение ![]() и откладывают
на оси ординат графика.
и откладывают
на оси ординат графика.
Из полученной точки проводится горизонтальная линия до пересечения с кривой принятого значения и из точки пересечения опускается перпендикуляр на ось абсцисс, по которой читается значение h.
Высоту водобойной стенки определяют по формуле ( VI.64)
![]()
Если р окажется меньше hбыт, следует перейти на расчет по графику для определения высоты затопленной водобойной стенки (см. рис. VI.39).
Рис. VI .39. График для определения высоты затопленных водобойных колодцев
при прямоугольном сечении отводящего русла
На графике по оси абсцисс нанесены значения функции
|
|
( VI.65) |
где ![]() и hкр принимаются по рис. VI.27.
и hкр принимаются по рис. VI.27.
По оси ординат нанесены значения функции
|
|
( VI.66) |
где hст также принимается по рис. VI.27.
Серия лучевых линий на графике представляет собой значения функции А, равной
|
|
( VI.67) |
По графику отыскивают hн и по нему вычисляют рст:
|
|
( VI.68) |
Таким образом, пользование графиком рис. VI.39 сводится к следующему:
1) по графику приложения (9) вычисляют hKp;
2) по формуле ( VI.58) вычисляют h"сж;
3) по формулам ( VI.65) и ( VI.67) вычисляют значения В и А;
4) определяют k по формуле ![]() .
.
На графике по оси абсцисс откладывают значение В, восстанавливают перпендикуляр до пересечения с соответствующей линией А; из точки пересечения проводят горизонтальную прямую до пересечения с осью ординат, на которой читается значение hн.
По известному hн решают уравнение ( VI.66).
РАСЧЕТЫ ПРЯМОУГОЛЬНЫХ ВОДОБОЙНЫХ КОЛОДЦЕВ И ВОДОБОЙНЫХ СТЕНОК ПО УПРОЩЕННОМУ СПОСОБУ акад. Е.А. ЗАМАРИНА
На стадии проектного задания, а также для менее ответственных сооружений (на дорогах II категории и ниже) можно пользоваться достаточно простым способом акад. Е.А. Замарина, по которому размеры водобойных колодцев и водобойных стенок получаются несколько меньшими, чем по обычным расчетам, т. е. сооружения получаются с меньшими запасами, достаточными, однако, для сохранности сооружений.
Этот способ заключается в следующем.
1. Определяют сжатую глубину
|
|
( VI.69) |
где q - удельный расход;
h0 - установившаяся нормальная глубина в быстротоке (при равномерном движении);
vn - скорость воды над перепадом;
р - расстояние от перепада до поверхности воды в колодце;
j - коэффициент скорости;
|
p |
1 |
2 |
3 |
4 |
5 |
6 |
|
j |
0,97 |
0,95 |
0,91 |
0,88 |
0,86 |
0,85 |
2. Определяют сопряженную глубину
|
|
( VI.70) |
3. Глубину колодца определяют по формуле
|
d = 1,05h" - h кр ; |
( VI.71) |
4. Определяют длину колодца
|
|
( VI.72) |
ПОРЯДОК РАСЧЕТА ВОДОБОЙНОЙ СТЕНКИ (рис. VI. 40):
1. hсж и h" определяют так же, как и при расчете колодца, но в формулу ( VI.69) подставляют не р, а р' = р - с, для чего в первом приближении задаются высотой стенки с.
2. Определяют скоростной напор перед водобойной стенкой
![]()
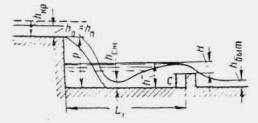
Рис. VI .40. Схема расчета водобойной стенки
3. Определяют полный напор над водобойной стенкой
4. Вычисляют напор над стенкой (без скоростного напора)
H = H0 - hv.
5. Определяют высоту стенки с
c = 1,05h" - H.
Эту высоту сравнивают с высотой с, которой задались в первом приближении, и если с » с' (с точностью до 10 %), расчет продолжают дальше; при значительном же расхождении расчет производится снова при другом значении с'.
6. Вычисляют расстояние L от стенки падения до водобойной стенки
![]()
ПЕРЕПАДЫ
Перепады устраивают в тех случаях, когда на протяжении косогорного сооружения (трубы, подводящего русла, водоотвода и т. д.) нежелательно возникновение больших скоростей течения по условиям прохода потока в самом сооружении или по условиям гашения энергии потока за сооружением.
В зависимости от разности отметок на входе и выходе устраивают одноступенчатый или многоступенчатый перепад.
ОДНОСТУПЕНЧАТЫЙ ПЕРЕПАД
При необходимости излишняя кинетическая энергия потока после слива его с перепада гасится при помощи водобойного колодца или водобойной стенки.
В случае устройства перепада «в голове сооружения» для гашения может быть применена водобойная стенка. При таком расположении перепада лоток сооружения располагают в уровне нижнего бьефа, что имеет известные преимущества, так как поток входит в отверстие успокоенным Кроме того, труба при таком расположении перепада становится более устойчивой.
К недостаткам перепада «в голове сооружения» относится ограничение в гашении энергии, обусловливаемое высотой насыпи. Кроме того, труба получается удлиненной.
В случае устройства перепада на выходе из трубы или в подмостовом лотке для гашения может применяться водобойная стенка, водобойный колодец или комбинация этих двух сооружений.
МНОГОСТУПЕНЧАТЫЙ ПЕРЕПАД
Назначение многоступенчатого перепада заключается в том, чтобы на каждой его ступени избыточная кинетическая энергия потока, слившегося с перепада, была погашена до своего минимума и поток приобретал в конце ступени критическую глубину hкр; Для этого длина перепада должна быть достаточной для образования на пороге такой глубины (рис.. VI.41, а).
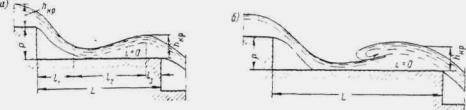
Рис. VI .41. Многоступенчатый перепад:
а -нормальной длины; б - длины, при которой образуется отогнанный прыжок
Длина перепада может быть и несколько большей. В таком случае на перепаде образуется отогнанный прыжок с кривой спада, в конце которой также образуется критическая глубина (рис. VI.41, б).
Устройство длинных ступеней обычно вызывается более пологим уклоном местности.
Таким образом, расчет многоступенчатого перепада сводится к определению наименьшей длины ступени L.
Полная длина ступени L складывается из трех участков (см. рис. VI.41, а): l1 - длины полета струи, слившейся с предыдущего перепада; l2 - длины кривой подпора, на которой поток достигает критической глубины, и l 3 - длины кривой спада от глубины hKp до ребра ступени, т. е.
L = l1 + l2 + l3
В случае горизонтальных ступеней 11 определяют по формуле ( VI.48) или по графику рис. VI.33; 12 может быть определено по упрощенному уравнению Журина:
|
|
( VI.73) |
где iкр определяют по формуле (1.17);
hсж - глубина слившейся струи,
![]()
vсж определяют по формуле
![]()
h Kp можно определять по графику приложения 9
i3 приближенно может быть принято равным
|
l 3 = (2 ¸ 2,5)hкр . |
(VI.74) |
Таким образом, полная длина ступени
|
|
( VI.75) |
Если по местным условиям при данной высоте перепада р его длина L окажется равной или большей вычисленной по формуле ( VI.75), то на этом расчет многоступенчатого перепада с горизонтальной ступенью заканчивается.
В сухих логах длинным ступеням полезно придавать небольшой уклон ( i = 0,005) с тем, чтобы после прохода паводка вода не задерживалась на ступенях. Расчет длины такой наклонной ступени производится также по формуле ( VI. 75).
Величины l1 и l3 вычисляют по формулам ( VI.48) и ( VI.74);
l2 при уклоне ступени, не превышающем 0,01, может быть вычислено как для горизонтальной ступени.
Рис. VI .42. Схема многоступенчатого перепада

Рис. VI .43. Перепад с обратным уклоном ступеней
Если L окажется менее получаемой по формуле ( VI.75), то энергия на пороге ступени не будет гаситься, а наоборот, будет нарастать со ступени на ступень, так что в конце концов струя может проскочить мимо ступени (рис. VI.42).
На круто падающих косогорах для ускорения гашения энергии и уменьшения длины ступени каждой из них придают обратный уклон ( i < 0) (рис. VI.43), величина которого обычно принимается равной 0,01-0,02. Длина такой ступени определяется по той же формуле ( VI.75).
На рис. VI.43 пунктиром показана прорезь для выпуска воды из пазухи во избежание ее замерзания. Однако необходимо заметить, что, несмотря на устройство таких прорезей, опасность замерзания воды в пазухе полностью не исключается, ввиду чего применять такие перепады следует с осторожностью.
При очень крутом падении лога бывает целесообразно уменьшать высоту перепадов р, одновременно уменьшая и их длину L1 и рассматривать весь многоступенчатый перепад как быстроток с повышенной шероховатостью, значение коэффициента шероховатости для которой может приниматься по указаниям стр. 85.
Высота перепадов р при этом не должна превосходить предела ( при котором они еще могут рассматриваться как элементы повышенной шероховатости), определяемого соотношением
|
p ≤ 1/2 hкр . |
(VI.76) |
В случае если высота перепадов окажется больше допускаемой соотношением ( VI.76), она может быть искусственно уменьшена путем устройства наклонных участков лотка ступенчатого русла, как показано пунктиром на рис. VI.42.
Ведя расчет ступенчатых перепадов, следует также иметь в виду, что поток на них значительно аэрируется и поэтому коэффициент шероховатости для него увеличивается в соответствии с указаниями стр. 78 и 79.
Как правило, ширина перепада известна, так как она равна ширине подводящего быстротока или трубы; если же эта ширина неизвестна, ею необходимо задаться.
МНОГОСТУПЕНЧАТЫЙ ПЕРЕПАД КОЛОДЕЗНОГО ТИПА
Если применение ступеней с обратным уклоном оказывается недостаточным для гашения энергии потока на перепаде, а удлинить ступень невозможно, прибегают к устройству на пороге небольшой водобойной стенки, т. е. образуется перепад колодезного типа (рис. VI.44).
Ступени такого перепада делаются горизонтальными, а расчет производится из условия, что на каждой ступени образуется затопленный прыжок воды. Методы расчета ступени здесь во всем аналогичны расчетам водобойных колодцев, описанных в предыдущем параграфе.
Рис. VI .44. Перепад колодезного типа
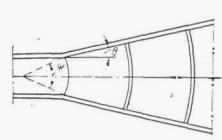
Рис. VI .45. Веерный перепад
Иногда для еще более интенсивного гашения энергии косогорного потока перепады устраивают уширяющимися в плане в виде веера (рис. VI.45). В таком случае водобойным стенкам на порогах полезно придать криволинейное очертание, причем центральный угол такой стенки делают в 3-4 раза больше угла роспуска перепада, т. е. j = (3 ¸ 4) q.
Расчет такого перепада может производиться аналогично расчету ряда расширяющихся колодцев.
КОНСОЛЬНЫЙ ВОДОСБРОС
При благоприятных местных условиях консольный водосброс (рис. VI.46) может оказаться наиболее рациональной и экономичной конструкцией.
В консольном водосбросе различают быстротечный лоток lл и струенаправляющий носок lн. Последний делают горизонтальным или слегка приподнятым под углом c для увеличения дальности полета струи (рис. VI.47).
Разность между прямым уклоном лотка и обратным уклоном носка во избежание возникновения явлений гидравлического удара должна быть достаточно мала. Поэтому рекомендуется при уклонах лотка до 250‰ угол c принимать не более 15 °, а при больших уклонах лотка носок делать горизонтальным.
Длину носка lн не рассчитывают, а принимают обычно по конструктивным соображениям от 1 до 2 м.
Гидравлический расчет консольного водосброса слагается из трех элементов:
расчета быстротока;
определения дальности полета струи;
определения размеров воронки размыва в месте падения струи.
Расчет быстротока консоли выполняется по указаниям стр. 79 и 80 и имеет целью определение глубины потока h0 и скорости v0 в конце консоли у перехода на носок.
Величина v0 не должна превосходить допускаемую по материалу лотка, исходя из чего подбирают уклон консоли.
При определении дальности полета струи глубину воды и скорость течения в конце носка ввиду малой его длины принимают такими же, как и в конце консоли, т. е. равными h0 и v 0 (см. рис. VI.47).
В таком случае дальность полета струи l1 с носка, имеющего обратный уклон, будет
|
|
( VI.77) |
При горизонтальном носке формула ( VI.77) принимает вид
|
|
( VI.78) |
Анализ уравнений дальности полета струи с носка показывает, что наибольшая дальность полета при угле наклона носка c в пределах 0-15° получается при соотношении высот, преодолеваемых потоком, H1 и H (см. рис. VI.47), большим 0,5, но меньшим 1, т. е.
![]() .
.
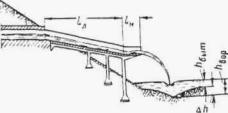
Рис. VI .46. Консольный водосброс
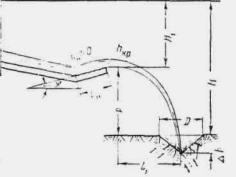
Рис. VI .47. Струенаправляющий носок консольного водосброса
При горизонтальном носке то же получается при ![]() .
.
Для определения дальности полета струи с носка можно пользоваться табл. VI.5, в которой приводятся значения относительной дальности полета
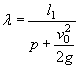
в зависимости от размеров относительной высоты консоли
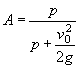
Таблица VI.5
Значения относительной дальности полета струи
|
i н |
A |
||||||||
|
0,285 |
0,3 |
0,375 |
0,4 |
0,444 |
0,5 |
0,6 |
0,7 |
0,8 |
|
|
0 |
- |
0,906 |
- |
0,980 |
- |
1,000 |
0,380 |
0,916 |
0,800 |
|
0,1 |
- |
0,060 |
- |
1,099 |
1,105 |
1,100 |
1,058 |
0,974 |
0,837 |
|
0,2 |
- |
1,212 |
1,225 |
1,224 |
- |
1,197 |
1,138 |
1,022 |
0,866 |
|
0,3 |
1,362 |
1,361 |
- |
1,340 |
- |
1,287 |
1,192 |
1,062 |
0,866 |
По известному λ находится l1 по формуле
|
|
( VI.79) |
Размеры воронки размыва определяются по графику проф. М С. Вызго (рис. VI.48). График дает значение глубины воды в воронке. Глубина размыва Δ h получается по формуле
![]()
Для пользования графиком необходимо знать q - удельный расход консоли, р - высоту падения струи и вычислить произведение qp. На графике значения q отложены по оси абсцисс. Каждое значение р представлено своей наклонной кривой.
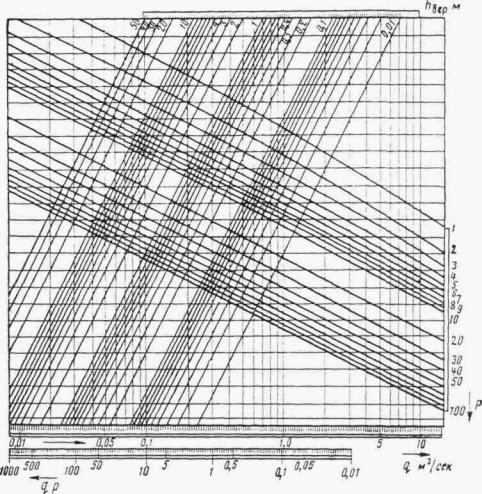
Рис. VI .48. График проф. М. С. Вызго для определения размеров воронки размыва за консольным водосбросом
Порядок пользования графиком следующий.
Из точки значения q восстанавливают перпендикуляр до пересечения с линией р. Из точки значений qp (на шкале, параллельной оси абсцисс) восстанавливают другой перпендикуляр.
Из точки пересечения первого перпендикуляра с линией р проводят горизонтальную прямую до пересечения со вторым перпендикуляром. Наклонная прямая (поднимающаяся слева направо), проходящая через точку этого пересечения, указывает на значение h"во p.
Для определения диаметра воронки D условно принимается форма воронки в виде конуса с уклонами граней 1:1 (см. рис. VI.46, VI.47).
РАСЧЕТ ОТВОДНОГО РУСЛА
Устройство за косогорными трубами (или мостами) различных гасителей не исключает необходимости укрепления отводного русла (нижнего бьефа), так как большая энергия потока не может целиком гаситься указанными сооружениями.
Расчеты укрепления нижнего бьефа изложены в главе V, однако расчеты отводного русла за гасителями ЦНИИСа или за расширяющимся водобойным колодцем имеют специфику (рис. VI.49).
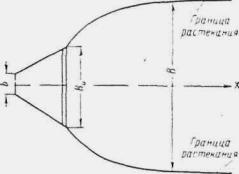
Рис. VI .49. Схема растекания потока в отводном русле за гасителем
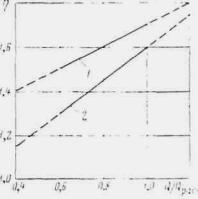
Рис. VI .50. График для определения h :
1 -расширяющиеся колодцы; 2 - гасители ЦНИИСа
Методика расчетов такого отводного русла, разработанная ЦНИИСом, состоит в следующем.
1. Определяют среднюю скорость потока на выходе из гасителя
v0 = 0,45 vвых
где vвых определяют по формуле ( II.5).
2. Гидравлические характеристики потока в отводном русле определяют по уравнению Бернулли методом Чарномского (см. формулу 1.7).
3. При свободном растекании в нижнем бьефе ширину потока определяют по формулам:
при гасителе в виде расширяющегося водобойного колодца
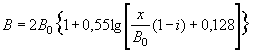
при гасителе ЦНИИСа
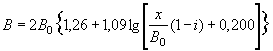
при гасителе ЦНИИСа с уменьшенным углом раструбности ширина потока уменьшается по сравнению с предыдущей формулой на величину
2 L (0,577 - tg j/2);
при раструбе, образованном вертикальными стенками, расходящимися в плане под углом 15-20 ° с осью сооружения и имеющем дно без повышенной шероховатости, а также при типовом выходном оголовке
![]()
![]()
где х - расстояние от конца раструба вдоль продольной оси сооружения;
i - уклон отводного русла;
В 0 - ширина выхода из гасителя или оголовка.
При уклоне отводного русла i ≤ 0,05 можно принимать i = 0.
4. Глубину ямы .местного размыва Т в неукрепленном отводном русле определяют формулой
![]()
где hрр - глубина, формируемая в данном грунте равномерным спокойным потоком с удельным расходом q = hivi;
hiи vi - средние глубина и скорость потока в конце укрепления;
hбыт - бытовая глубина воды в нижнем бьефе;
μ - коэффициент, зависящий от геометрических форм и условий работы сооружения
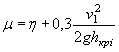
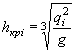 - критическая
глубина в конце укрепления, значения величины h принимают по графику
рис. VI.50;
- критическая
глубина в конце укрепления, значения величины h принимают по графику
рис. VI.50;
ψ- коэффициент, зависящий от устройства в конце укрепления:
при устройстве в конце укрепления отвесного зуба ψ = 1,
при устройстве же в конце укрепления откоса 1:1,5 ψ = 1,35;
h pp - определяется по формуле Б. И. Студеничникова
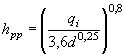
d - средний диаметр фракций грунта.
ГЛАВА VII
РАСЧЕТЫ КАНАВ
ОБЩИЕ ПОЛОЖЕНИЯ
Сооружения, отводящие воду от железнодорожного земляного полотна (водоотводные и нагорные канавы, искусственные русла, резервы), могут иметь различное поперечное сечение.
Наиболее распространенным поперечным сечением является трапецеидальное, реже применяется треугольное и прямоугольное.
Основные параметры трапецеидального сечения (рис. VII.1):
ширина по дну b;
ширина живого сечения поверху В;
глубина наполнения h;
строительная глубина H;
коэффициент откоса т = ctg а = a/ h;
относительная ширина по дну β = b/ h;
относительная глубина по дну ξ = h/ b = 1/ β.
Ширина канавы по дну принимается не менее 0,6 м, на болотах - не менее 0,8 м, а на лесовозных ветках и на путях карьеров - не менее 0,5 м.
Низовая бровка канавы должна возвышаться над уровнем расчетного горизонта воды не менее чем на 20 см.
Рис. VII .1. Поперечное сечение
Формулы, характеризующие сечение: площадь живого сечения
|
w = (b + mh)h = (β+ m)h2; |
( VII.1) |
смоченный периметр канавы
|
|
( VII.2) |
гидравлический радиус
![]()
где т' = 2 ![]() .
.
С гидравлической точки зрения форма поперечного сечения канавы должна приниматься такой, чтобы условия протекания воды были наилучшими: канава должна иметь гидравлически наивыгоднейшее поперечное сечение, которое при одной и той же площади, шероховатости и уклоне дна пропускает наибольший расход.
Гидравлически наивыгоднейшая относительная ширина по дну
|
|
( VII.3) |
Таблица VII.1
Значения βгн,
и m' = 2 ![]() для
гидравлически наивыгоднейшего трапецеидального сечения
для
гидравлически наивыгоднейшего трапецеидального сечения
|
m |
0 |
0,10 |
0,20 |
0,25 |
0,50 |
0,75 |
1.0 |
1,25 |
1,50 |
2,0 |
2,50 |
3,0 |
|
|
2,0 |
1,810 |
1,640 |
1,562 |
1,236 |
1,000 |
0,828 |
0,702 |
0,606 |
0,472 |
0,385 |
0,325 |
|
2,0 |
2,010 |
2,040 |
2,062 |
2,236 |
2,500 |
2,828 |
3,202 |
3,606 |
4,472 |
5,385 |
6,324 |
По табл. VII. 1 можно легко определить размеры гидравлически наивыгоднейшего трапецеидального сечения.
Например, при откосах канавы 1:1,5 и ширине ее по дну 0,6 м глубина живого сечения должна быть
![]()
Если по местным условиям глубина живого сечения должна быть принята h = 0,6 м, то при коэффициенте откоса т = 1:1,5 ширина канавы по дну будет
b = βh = 0,606·0,60 =0,36 м .
Гидравлически наивыгоднейшие сечения канав с коэффициентом откоса более 0,5 имеют относительно большие глубины при незначительной ширине по дну, что в большинстве случаев является нежелательным. В результате увеличивается стоимость 1 м3 земляных работ, повышаются потери воды на фильтрацию. Поэтому на практике чаще применяются сечения с относительной шириной β больше гидравлически наивыгоднейшей относительной ширины β0.
Исследованиями, проведенными в МИИТе канд. техн. наук М. И. Виноградовым, установлено, что увеличение относительной ширины β не вызывает значительного увеличения площади живого сечения канавы и, следовательно, незначительно уменьшает скорость течения воды.
Если скорость течения в канаве значительно превышает допустимую, то снижения скорости можно добиться только за счет уменьшения уклона, а не за счет уширения канавы.
Скорость течения воды в канавах должна быть такой, чтобы при расчетном расходе воды откосы и дно канавы не размывались, а с другой стороны, чтобы канава не заиливалась. Незаиливающие скорости vмин определяются количеством взвешенных частиц в потоке и размерами фракций d.
Для канав в обычном земляном русле при коэффициенте шероховатости п = 0,0225 и среднем диаметре преобладающей массы взвешенных наносов, равном dcp = 0,25 мм, критическая незаиливающая скорость в м/сек определяется по формуле И. И. Леви:
![]() ,
,
где R - гидравлический радиус в м.
Для обычных потоков в весенние или ливневые паводки эта скорость может приближенно приниматься по табл. VII.2.
Расчетный расход нагорных канав, принимающих воду с верхового склона, изменяется (увеличивается) на всем протяжении канавы; в расчетах этих канав учитывается ступенчатое изменение расхода по отдельным участкам длиной 100-200 м.
Таблица VII. 2
Значения критических незаиливающих скоростей течения (при гидравлическом радиусе R = 1 м)
|
Средний размер фракции d в мм |
v мин в м/сек |
d c р в мм |
v мин в м/сек |
d c р в мм |
v мин в м/сек |
|
0,1 |
0,22 |
1,0 |
0,95 |
2,0 |
1,10 |
|
0,2 |
0,45 |
1,2 |
1,00 |
2,2 |
1,10 |
|
0,4 |
0,67 |
1,4 |
1,02 |
2,4 |
1,11 |
|
0,6 |
0,82 |
1,6 |
1,05 |
2,6 |
1,11 |
|
0,8 |
0,90 |
1,8 |
1,07 |
3,0 |
1,11 |
ОБЩИЙ МЕТОД РАСЧЕТА КАНАВ
Гидравлический расчет канав ведут по установившемуся равномерному режиму, т. е. при постоянстве расхода Q paсч и скорости течения v на каждом расчетном участке канавы.
Величину расхода определяют согласно Инструкции по расчету стока с малых бассейнов только на ливневой сток, причем для водосборных площадей F ≤ 0,2 км2, принимают постоянное значение λ = 0,01.
Для канав, расположенных в пределах станций, Q paсч определяют по методу, изложенному в книге П. С. Крутенкова и А. И. Хохорина «Водоотводные сооружения на железнодорожных станциях» (М., «Транспорт», 1966).
Таблица VII.3
Нормы вероятностей превышения расходов Q paсч
|
Железные дороги общей сети |
Железные дороги промышленных предприятии |
Железные дороги колеи 750 мм |
|||
|
Категория дороги |
Расчетная вероятность превышения в % |
Категория дороги |
Расчетная вероятность превышения в % |
Категория дороги |
Расчетная вероятность превышения в % |
|
I |
2 |
I и II |
5 |
Общей сети и подъездные пути |
5 |
|
II |
4 |
- |
- |
- |
- |
|
III и IV |
5 |
Все прочие пути |
10 |
Все прочие пути |
10 |
Основные расчетные уравнения:
![]()
![]() - расходная
характеристика;
- расходная
характеристика;
![]()
При расчетах канав могут иметь место следующие основные задачи.
1. Определить основные размеры сечений h и b по заданным т, Q, п, i. Задачу решаем методом приближения.
Так как две искомые величины связаны одним уравнением
![]() ,
,
то можно подобрать много значений b и h, удовлетворяющих этому уравнению.
Чтобы сделать задачу определенной, необходимо задаться
шириной канавы по дну b ,
глубиной h или
отношением ![]()
В соответствии с этим различаются три случая решения этой задачи:
а) задаемся шириной b, требуется найти h.
Эта задача решается следующим образом. Определяем ![]() ; зная b,
задаемся значением h = h1
; зная b,
задаемся значением h = h1
Определяем:
![]() ,
,
![]()
![]()
![]()
C1 определяем по приложению 7.
Если величина K1 достаточно близка к требуемой ![]() , то на этом расчет заканчивается; в противном случае надо
задаться новым значением h
= hz и
повторить расчет;
, то на этом расчет заканчивается; в противном случае надо
задаться новым значением h
= hz и
повторить расчет;
б) задаемся глубиной h1, требуется найти b.
Вычисляем ![]() , задаемся значением b, затем определяем w, c, R,С,
, задаемся значением b, затем определяем w, c, R,С, ![]() и сравниваем
вычисленную величину K с
требуемой
и сравниваем
вычисленную величину K с
требуемой ![]() . Если при принятом значении b расходная характеристика равна
требуемой, то задача решена;
. Если при принятом значении b расходная характеристика равна
требуемой, то задача решена;
в) задаемся отношением ![]() , требуется найти b и h.
, требуется найти b и h.
Определяем ![]() , затем, задаваясь значением h,
определяем b1
= β h, w, c, R,
С, и, наконец,
, затем, задаваясь значением h,
определяем b1
= β h, w, c, R,
С, и, наконец, ![]() . Вычисленную
расходную характеристику сравниваем с требуемой.
. Вычисленную
расходную характеристику сравниваем с требуемой.
2. Определить необходимый уклон дна i по заданным h, b, m, n, Q.
Определив гидравлические элементы w, c, R и коэффициент С, определяем
![]() , а затем уклон
, а затем уклон ![]()
3. Определить расход Q (или скорость v) по заданным h, b ,т, п, i
Находим гидравлические элементы w, c, R и коэффициент С, а затем величину ![]() и расход
и расход ![]() .
.
Расход Q можно определить и непосредственно по формуле
![]() .
.
Значения С определяют в зависимости от покровных условий (земляное русло, одерновка, мощение), по которым подбирается коэффициент шероховатости (см. приложение 5).
Для канав с неоднородной шероховатостью русла, например, для канав, стенки которых выложены дерном, а дно замощено камнем, вычисляют приведенный коэффициент шероховатости по формуле
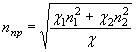
где ![]() 1 - часть периметра с коэффициентом n1
1 - часть периметра с коэффициентом n1
![]() 2 - часть периметра с коэффициентом nz;
2 - часть периметра с коэффициентом nz;
![]() - общий
смоченный периметр канавы, равный
- общий
смоченный периметр канавы, равный ![]() 1 +
1 + ![]() 2
2
В длинных канавах следует рассчитывать несколько сечений, отстоящих одно от другого не более чем на 100-200 м.
Если по условиям рельефа уклон канавы должен иметь переломы, то для участка с другим уклоном выполняют новые расчеты. Поперечное сечение канавы в таком случае оказывается уже заданным по предыдущему участку, и расчеты ведутся в следующем порядке.
По известным из предыдущего расчета С1 и R1 находят
скорость в конце следующего расчетного участка ![]() а затем площадь
живого сечения
а затем площадь
живого сечения ![]()
По известному v 2 находят соответствующую ему глубину h2 по формуле
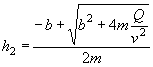
Рис VII .2. Продольный профиль канавы
В случае значительного расхождения h2 с прежним значением h1 определяют новые значения С2 и R2 и по ним корректируют скорость v2 и т. д. При необходимости устройства переломов продольного профиля дна русла нужно стремиться, чтобы каждый последующий участок продольного профиля имел больший продольный уклон, чем предыдущий участок.
В случаях необходимости перехода с большего уклона i1 на меньший i2 во избежание перелива воды из русла перелом дна должен сдвигаться вниз по течению, как показано на рис. VI 1.2; от точки сопряжения горизонтов воды участков i1 и i2 на величину (в м)
![]()
ПРИБЛИЖЕННЫЙ МЕТОД РАСЧЕТА КАНАВ
М. И. Виноградовым (МИИТ) установлено, что для решения задач по определению размеров живого сечения по заданным значениям β и т при условии, если значение показателя степени у в формуле принять постоянным, могут быть использованы следующие формулы:
|
|
( VII.4) |
для гидравлически наивыгоднейшего сечения
|
|
( VII.5) |
Как указывалось в главе I, проф. М. Д. Чертоусов считает возможным принять значение у:
а) при расчете русел с малой шероховатостью (0,010 ≤ п ≤ 0,015)
у = 1/6
б) при расчете русел со средней шероховатостью (0,015 < п < 0,025)
у = 1/5
в) при расчете русел с большой шероховатостью (п ≥ 0,025)
у = 1/4
На основе опыта проектных и строительных организаций СССР С. А. Гиршкан вывел эмпирическую зависимость для определения относительной ширины β по расходу канала:
|
|
( VII.6) |
где Q в м3/сек; формула применима для расходов от 0,1 до 1000 м3/сек.
Пример. Определить размеры сечения канала для расхода Q = 1 м3/сек при уклоне дна i= 0,0016 и коэффициенте откоса т = 1,5.
Решение. Определяем по уравнению ( VII.6) значение относительной ширины
![]()
Модуль расхода
![]() м3/сек.
м3/сек.
Принимаем значение коэффициента шероховатости
п = 0,0220 и y = 1/5;
тогда
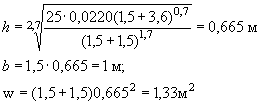
Определим для сравнения площадь гидравлически наивыгоднейшего сечения, вычислив предварительно:
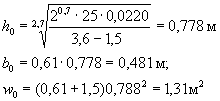 .
.
Соотношение площадей ![]() , т. е. для данного случая живое сечение на 1,5 % больше
гидравлически наивыгоднейшего.
, т. е. для данного случая живое сечение на 1,5 % больше
гидравлически наивыгоднейшего.
ГРАФО-АНАЛИТИЧЕСКИЕ МЕТОДЫ РАСЧЕТА КАНАВ
Общий метод расчета канав и русел, когда задача решается путем последовательных приближений, по своей трудоемкости не всегда удобен для практических целей, особенно если требуется в короткий срок рассчитать и запроектировать большое число водоотводов.
Существует ряд графо-аналитических методов расчета канав. Все они исходят из гидравлической модели равномерного движения жидкости и из предположения обязательности этого режима при любых сочетаниях размеров канав и пропускаемых ими расходов.
Наиболее удобными являются следующие графические приемы расчетов.
1. По номограммам Павловского
Академиком Н. Н. Павловским разработаны номограммы для расчета трапецеидальных земляных каналов для значений коэффициентов шероховатости русла 0,02; 0,0225; 0,025 и 0,03.
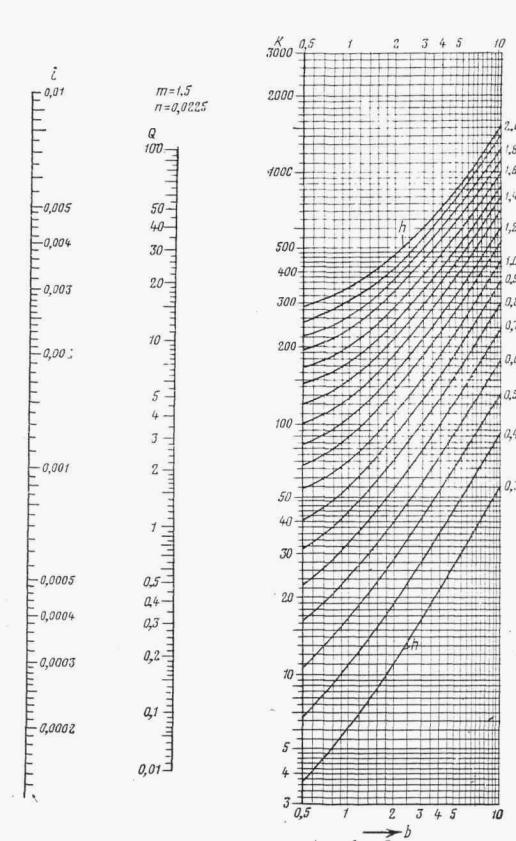
Рис. VI 1.3. Номограмма для расчета каналов по формуле Павловского при т = 1,5 и n = 0,0225
Номограммы предусматривают одно значение коэффициента откоса т = 1,5, ширину русла b от 0,5 до 20 м и глубину воды в нем h от 0,3 до 2 м.
Номограммы устанавливают зависимость между четырьмя переменными: Q, i, l и h.
Задаваясь двумя из них, можно, пользуясь номограммами, подобрать значения остальных.
Образец номограммы Павловского для случая, наиболее часто встречающегося в практике, приведен на рис. VII.3.
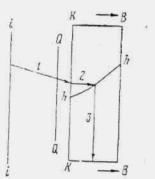
Рис. VII .4. Ключ к номограмме Павловского
На рис. VII.4 приведен порядок пользования номограммами Павловского, где номерные линии со стрелками указывают на последовательность нахождения величин; например, по заданным Q и i подобрать h и b.
Скорость течения при этом определяется обычным способом по формуле
![]()
2. По номограмме Спивакова-Иоффе
Номограмма Спивакова-Иоффе (Промтранспроект) устанавливает зависимость между пятью переменными: Q, i, b, h и v при неизменном т = 1,5 для грунтовых, одернованных и мощеных канав.
Порядок пользования номограммой и пример расчета приведены на рис. VII.5.
3. По графикам Промтранспроекта
Промтранспроектом составлены графики зависимости расхода и скорости течения воды от уклона дна канав шириной по дну от 0,4 до 1,4 м; одернованных при п - 0,035, мощеных при п = 0,022 и неукрепленных при n = 0,0275.
График зависимости расхода и скорости течения воды для т= 1,5, п = 0,0275 и ширине канавы по дну 0,6 м приведен на рис. VII.6.
ТАБЛИЦЫ ДЛЯ РАСЧЕТА КАНАВ (ТАБЛ. VII.4- VII.7)
Таблицы составлены Гипротранстэи по предложению канд. техн.
наук М. И. Виноградова. Таблицы основаны на следующих зависимостях: ![]() обозначая
обозначая ![]() , получаем
, получаем ![]() ,
, ![]() обозначая
обозначая ![]() , получаем
, получаем ![]() i
.
i
.
В таблицах приведены значения К и W.
Таблицы составлены для неукрепленных канав с коэффициентами откоса т, равными 1; 1,5 и 2, при коэффициенте п = 0,0275 и у = 1/4 и для укрепленных канав при коэффициенте откоса т = 1,5, значениях п = 0,022 и у = 1/5
Пример. Дано Q = 1 м3/сек; i = 0,005; п = 0,0275;
![]()
При коэффициенте откоса т = 1,5 для значения К = 14,2 находим b = 0,6 и h = 0,6. Как правило, может быть найдено несколько вариантов размеров канав, соответствующих данному значению К. Выбор размеров канавы проектировщик осуществляет в зависимости от местных условий.
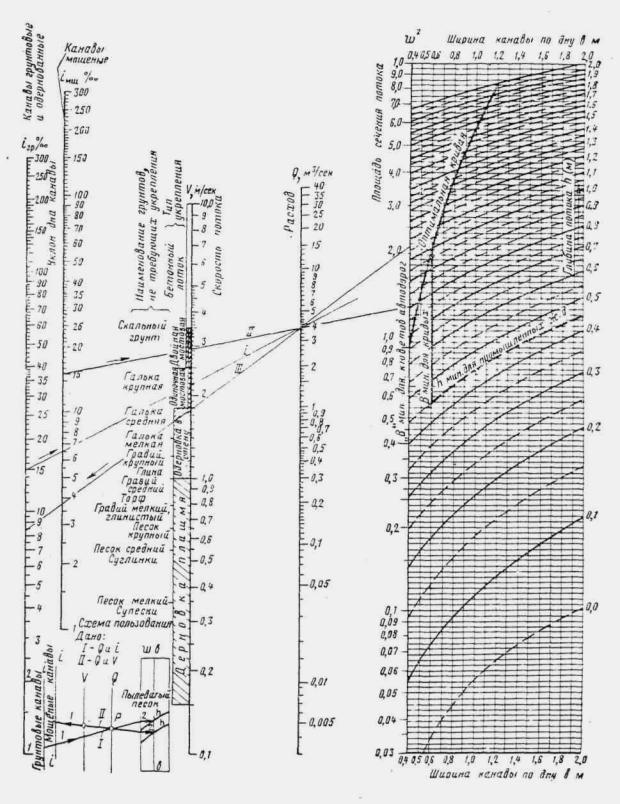
Рис. VII .5. Номограмма Спивакова-Иоффе
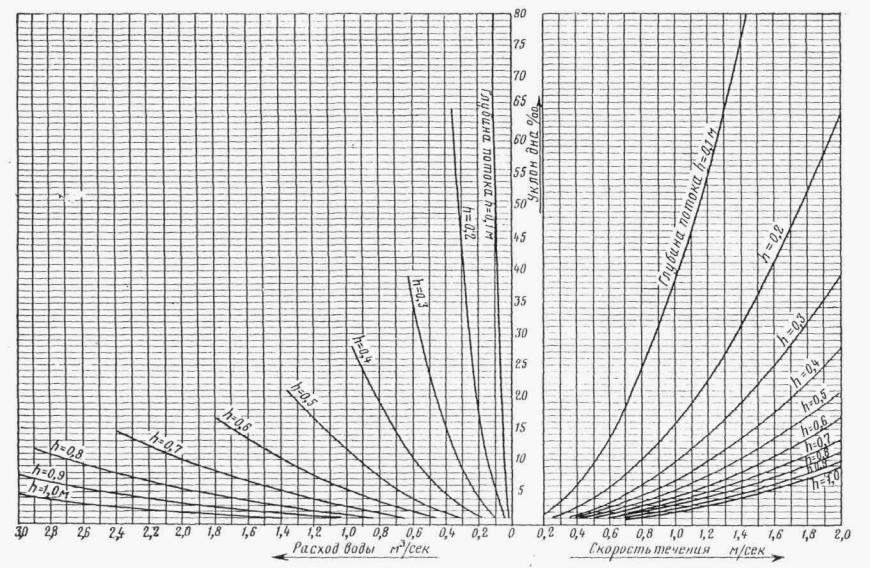
Рис. VII .6. График зависимости расхода и скорости течения воды от уклона дна неукрепленных канав
с коэффициентом шероховатости п = 0,0275 ( b = 0,6 м, откосы 1:1,5)
Таблица VII.4
Неукрепленные канавы (п =0,0275; у = 1/4; m = 1)
|
h |
b = 0,5 |
b = 0,6 |
b = 0,8 |
b = 1 |
||||
|
K |
W |
K |
W |
K |
W |
K |
W |
|
|
0,20 |
1,11 |
7,94 |
1,31 |
8,17 |
1,72 |
8,60 |
2,14 |
8,90 |
|
0,25 |
1,68 |
9,00 |
1,98 |
9,31 |
2,58 |
9,80 |
3,18 |
10,20 |
|
0,30 |
2,39 |
9,97 |
2,79 |
10,32 |
3,59 |
10,85 |
4,42 |
11,33 |
|
0,35 |
3,23 |
10,85 |
3,74 |
11,25 |
4,78 |
11,90 |
5,85 |
12,35 |
|
0,40 |
4,24 |
11,73 |
4,85 |
12,10 |
6,14 |
12,80 |
7,48 |
13,35 |
|
0,45 |
5,35 |
12,50 |
6,12 |
12,95 |
7,68 |
13,65 |
9,32 |
14,25 |
|
0,50 |
6,64 |
13,28 |
7,56 |
13,75 |
9,41 |
14,55 |
11,40 |
15,15 |
|
0,55 |
8,11 |
14,05 |
9,16 |
14,50 |
11,35 |
15,30 |
13,65 |
16,00 |
|
0,60 |
9,78 |
14,75 |
11,0 |
15,25 |
13,53 |
16,10 |
16,05 |
16,75 |
|
0,65 |
- |
- |
12,97 |
15,95 |
15,85 |
16,88 |
18,85 |
17,55 |
|
0,70 |
- |
- |
15,15 |
16,65 |
18,45 |
17,60 |
21,80 |
18,30 |
|
0,75 |
- |
- |
- |
- |
21,20 |
18,25 |
25,00 |
19,05 |
|
0,80 |
- |
- |
- |
- |
24,10 |
18,90 |
28,50 |
19,70 |
|
0,85 |
- |
- |
- |
- |
27,45 |
19,56 |
32,10 |
20,40 |
|
0,90 |
- |
|
- |
- |
31,00 |
20,25 |
36,00 |
21,10 |
|
0,95 |
- |
|
- |
- |
- |
- |
40,30 |
21,70 |
|
1,00 |
- |
- |
- |
- |
- |
- |
44,70 |
22,35 |
|
1,05 |
- |
- |
- |
- |
- |
- |
49,60 |
23,10 |
|
1,10 |
- |
- |
- |
- |
- |
- |
54,60 |
23,65 |
|
1,15 |
- |
- |
- |
- |
- |
- |
60,00 |
24,20 |
|
1,20 |
- |
- |
- |
- |
- |
- |
65,50 |
24,80 |
Таблица VII.5
Неукрепленные канавы (п =0,0275; у = 1/4; m = 1,5)
|
h |
b = 0,5 |
b = 0,6 |
b = 0,8 |
b = 1 |
||||
|
K |
W |
K |
W |
K |
W |
K |
W |
|
|
0,20 |
1,07 |
7,95 |
1,47 |
8,30 |
1,88 |
8,55 |
2,28 |
8,80 |
|
0,25 |
1,97 |
9,03 |
2,28 |
9,38 |
2,84 |
9,79 |
3,46 |
10,10 |
|
0,30 |
2,88 |
10,10 |
3,27 |
10,38 |
4,08 |
10,90 |
4,90 |
11,25 |
|
0,35 |
3,97 |
11,09 |
4,52 |
11,40 |
5,53 |
11,90 |
6,59 |
12,34 |
|
0,40 |
5,28 |
12,00 |
5,90 |
12,30 |
7,19 |
12,85 |
8,57 |
13,38 |
|
0,45 |
6,80 |
12,85 |
7,55 |
13,16 |
9,14 |
13,75 |
10,78 |
14,30 |
|
0,50 |
8,54 |
13,70 |
9,46 |
14,15 |
11,31 |
14,60 |
13,30 |
15,20 |
|
0,55 |
10,60 |
14,50 |
11,71 |
14,95 |
13,90 |
15,55 |
16,15 |
16,10 |
|
0,60 |
12,85 |
15,30 |
14,15 |
15,70 |
16,85 |
16,50 |
19,30 |
16,95 |
|
0,65 |
- |
- |
16,90 |
16,50 |
19,84 |
17,15 |
22,75 |
17,75 |
|
0,70 |
- |
- |
20,00 |
17,30 |
23,30 |
17,98 |
26,70 |
18,60 |
|
0,75 |
- |
- |
- |
- |
27,20 |
18,90 |
30,90 |
19,35 |
|
0,80 |
- |
- |
- |
- |
31,25 |
19,50 |
35,48 |
20,15 |
|
0,85 |
- |
- |
- |
- |
35,70 |
20,22 |
40,80 |
20,90 |
|
0,90 |
- |
- |
- |
- |
40,50 |
20,90 |
45,60 |
21,60 |
|
0,95 |
- |
- |
- |
- |
- |
- |
51,50 |
22,35 |
|
1,00 |
- |
- |
- |
- |
- |
- |
57,60 |
23,05 |
|
1,05 |
- |
- |
- |
- |
- |
- |
64,40 |
23,80 |
|
1,10 |
- |
- |
- |
- |
- |
- |
71,00 |
24,40 |
|
1,15 |
- |
- |
- |
- |
- |
- |
78,20 |
25,30 |
|
1,20 |
- |
- |
- |
- |
- |
- |
90,40 |
25,85 |
Таблица VII.6
Неукрепленные канавы (п =0,0275; у = 1/4; m = 2)
|
h |
b = 0,5 |
b = 0,6 |
b = 0,8 |
b = 1 |
||||
|
K |
W |
K |
W |
K |
W |
K |
W |
|
|
0,20 |
1,41 |
7,83 |
1,61 |
8,03 |
2,01 |
8,40 |
2,42 |
8,65 |
|
0,25 |
2,24 |
8,95 |
2,53 |
9,19 |
3,12 |
9,77 |
3,74 |
9,92 |
|
0,30 |
3,29 |
10,00 |
3,67 |
10,25 |
4,48 |
10,70 |
5,28 |
11,05 |
|
0,35 |
4,63 |
11,00 |
5,12 |
11,27 |
6,16 |
11,75 |
7,22 |
12,15 |
|
0,40 |
6,23 |
12,33 |
6,82 |
12,22 |
8,19 |
12,75 |
9,48 |
13,15 |
|
0,45 |
8,10 |
12,85 |
8,87 |
13,15 |
10,47 |
13,70 |
12,06 |
14,10 |
|
0,50 |
10,33 |
13,78 |
11,23 |
14,06 |
13,15 |
14,60 |
15,10 |
15,10 |
|
0,55 |
12,87 |
14,65 |
14,00 |
14,92 |
16,18 |
15,50 |
18,48 |
15,95 |
|
0,60 |
15,80 |
15,50 |
17,00 |
15,80 |
19,65 |
16,35 |
22,20 |
16,85 |
|
0,65 |
- |
- |
20,40 |
16,60 |
23,50 |
17,20 |
26,40 |
17,65 |
|
0,70 |
- |
- |
24,40 |
17,40 |
27,65 |
17,95 |
31,10 |
18,50 |
|
0,75 |
- |
- |
- |
- |
32,40 |
18,75 |
36,40 |
19,40 |
|
0,80 |
- |
- |
- |
- |
37,50 |
19,60 |
41,80 |
20,04 |
|
0,85 |
- |
- |
- |
- |
43,30 |
20,40 |
47,80 |
20,85 |
|
0,90 |
- |
- |
- |
- |
49,70 |
21,10 |
54,50 |
21,65 |
|
0,95 |
- |
- |
- |
- |
- |
- |
61,70 |
22,40 |
|
1,00 |
- |
- |
- |
- |
- |
- |
69,20 |
23,05 |
|
1,05 |
- |
- |
- |
- |
- |
- |
77,50 |
23,80 |
|
1,10 |
- |
- |
- |
- |
- |
- |
86,50 |
24,60 |
|
1,15 |
- |
- |
- |
- |
- |
- |
95,90 |
25,25 |
|
1,20 |
- |
- |
- |
- |
- |
- |
106,50 |
26,00 |
Таблица VII.7
Укрепленные канавы (п =0,0275; у = 1/5; m = 2)
|
h |
b = 0,5 |
b = 0,6 |
b = 0,8 |
b = 1 |
||||
|
K |
W |
K |
W |
K |
W |
K |
W |
|
|
0,20 |
1,75 |
10,9 |
2,03 |
11,25 |
2,58 |
11,75 |
3,16 |
12,10 |
|
0.25 |
2,71 |
12,4 |
3,11 |
12,74 |
3,90 |
13,30 |
4,74 |
13,75 |
|
0,30 |
3,91 |
13,7 |
4,42 |
14,10 |
5,51 |
14,70 |
6,61 |
15,22 |
|
0,35 |
5,36 |
14,9 |
6,05 |
15,35 |
7,42 |
16,00 |
8,82 |
16,53 |
|
0,40 |
7,10 |
16,1 |
7,93 |
16,54 |
9 64 |
17,20 |
11,40 |
17,80 |
|
0,45 |
9,07 |
17,2 |
10,10 |
17,63 |
12,20 |
18,40 |
14,35 |
19,05 |
|
0,50 |
11,43 |
18,3 |
12,65 |
18,70 |
15,05 |
19,35 |
17,65 |
20,15 |
|
0,55 |
14,02 |
19,2 |
15,45 |
19,75 |
18,43 |
20,50 |
21,35 |
21,30 |
|
0,60 |
17,11 |
20,3 |
18,70 |
20,75 |
22,00 |
21,45 |
25,40 |
22,30 |
|
0,65 |
- |
- |
22,40 |
21,75 |
26,10 |
22,60 |
29,90 |
23,30 |
|
0,70 |
- |
- |
26,20 |
22,70 |
30,45 |
23,50 |
34,85 |
24,30 |
|
0,75 |
- |
- |
- |
- |
35,50 |
24,65 |
40,20 |
25,25 |
|
0,80 |
- |
- |
- |
- |
40,50 |
25,40 |
46,20 |
26,15 |
|
0,85 |
- |
- |
- |
- |
46,50 |
26,30 |
52,30 |
27,10 |
|
0,90 |
- |
- |
- |
- |
52,30 |
27,10 |
59,10 |
27,90 |
|
0,95 |
- |
- |
- |
- |
- |
- |
66,40 |
28,90 |
|
1,00 |
- |
- |
- |
- |
- |
- |
К, 10 |
29,70 |
|
1,05 |
- |
- |
- |
- |
- |
- |
82,60 |
30,65 |
|
1,10 |
- |
- |
- |
- |
- |
- |
91,00 |
31,30 |
|
1,15 |
- |
- |
- |
- |
- |
- |
100,50 |
32,10 |
|
1,20 |
- |
- |
- |
- |
- |
- |
111,00 |
32,90 |
ГЛАВА VIII
ФИЛЬТРУЮЩИЕ НАСЫПИ И БРОДЫ
На железных дорогах общего пользования III и IV категорий, на промышленных дорогах широкой и узкой колеи и на автомобильных дорогах III, IV и V категорий при малых расходах воды и незначительном количестве взвешенных частиц грунта в потоке допускается применение фильтрующих насыпей и комбинированных фильтрующих сооружений.
Рис. VIII . 1. Напорная фильтрующая насыпь
Рис. VIII .2. Безнапорная фильтрующая насыпь
Турбулентная (квадратическая) фильтрация в крупнообломочном материале (камне) может быть:
а) напорной, когда фильтрационный поток ограничен со всех сторон грунтом насыпи (рис. VIII. 1);
б) безнапорной, когда фильтрационный поток имеет свободную поверхность, соприкасающуюся с воздухом в фильтрующей прослойке (рис. VIII.2).
РАСЧЕТ НАПОРНЫХ ФИЛЬТРУЮЩИХ НАСЫПЕЙ
Глубину воды перед фильтрующей насыпью Н определяют из уравнения
|
|
( VIII.1) |
где а - высота каменной фильтрующей прослойки;
l - длина ее по направлению течения;
I - уклон фильтрующей прослойки, обычно равный уклону лога;
Iф - гидравлический уклон, необходимый для фильтрации, определяемый по формуле
![]()
b - ширина фильтрующей прослойки;
k - коэффициент турбулентной фильтрации, определяемый по табл. VIII.1 в зависимости от размеров и формы камня.
Если глубина воды задана, то искомыми являются ширина прослойки b, или ее высота а (в том случае, когда ширину назначают по размерам лога).
Таблица VIII.1
Значение коэффициента турбулентной фильтрации k в м/сек
|
Средний диаметр камней, приведенных к шару, в см |
Коэффициент k при камнях |
Средний диаметр камней, приведенных к шару, в см |
Коэффициент k при камнях |
||||
|
окатанных |
промежуточного типа |
рваных остроугольных |
окатанных |
промежуточного типа |
рваных остроугольных |
||
|
5 |
0,15 |
0,17 |
0,19 |
25 |
0,39 |
0,44 |
0,49 |
|
10 |
0,23 |
0,26 |
0,29 |
30 |
0,43 |
0,50 |
0,53 |
|
15 |
0,30 |
0,33 |
0,37 |
40 |
0,50 |
0,56 |
0,62 |
|
20 |
0,35 |
0,39 |
0,43 |
50 |
0,56 |
0,63 |
0,70 |
Пример. Определить глубину воды перед напорной фильтрующей прослойкой размерами b = 20 м и а = 1 м при круглых (окатанных) камнях размером в поперечнике 25 см и расходе Q = 2 м3/сек. Дно прослойки горизонтальное; длина прослойки 30 м.
По табл. VIII.1 определяем k = 0,39 м/сек;
![]()
Н = 0,5 + 30 (0,0656) =0,5 + 1,97 = 2,47 м > 1 м,
т. е. насыпь действительно напорная.
РАСЧЕТ БЕЗНАПОРНЫХ ФИЛЬТРУЮЩИХ НАСЫПЕЙ
Глубину воды перед безнапорной фильтрующей насыпью определяют (считая, что уклон дна практически не влияет на протекание) по формуле
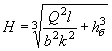
где hб - бытовая глубина в отводящем русле
Обычно бытовой глубиной в расчетах пренебрегают. Тогда
|
|
( VIII.2) |
Если глубина воды задана, то расчетной оказывается ширина фильтрующей дамбы b.
Пример. Для данных предыдущего примера рассчитать глубину воды перед сооружением.
Принимая b = 20 м, имеем
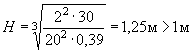
что показывает действительную невозможность пропуска расчетного расхода без напора через прослойку высотой 1 м.
Высота каменной фильтрующей безнапорной насыпи должна быть более H = 1,25 м.
ГИДРАВЛИЧЕСКИЙ РАСЧЕТ БРОДОВ
На автомобильных дорогах в некоторых случаях, чаще на горных дорогах низких категорий, применяются так называемые броды, т. е. перепуски воды через полотно дороги по лоткам, устраиваемым в проезжей части в пониженных местах продольного профиля.
Такие броды обычно имеют очертание в виде вогнутой круговой кривой, радиус которой зависит от категории дороги и местных условий, но должен быть не менее 200 м.
Расчет бродов ведется в следующем порядке.
1. В зависимости от категории дороги и местных условий принимают величину радиуса кривой лотка брода r.
2. Задаются глубиной потока в месте перелива h по пониженной точке живого сечения брода. Эта глубина обычно принимается не более 0,3 м.
3. Определяют площадь живого сечения брода в м2 при принятых значениях r и h:
|
|
( VIII.3) |
где j определяется из равенства
![]()
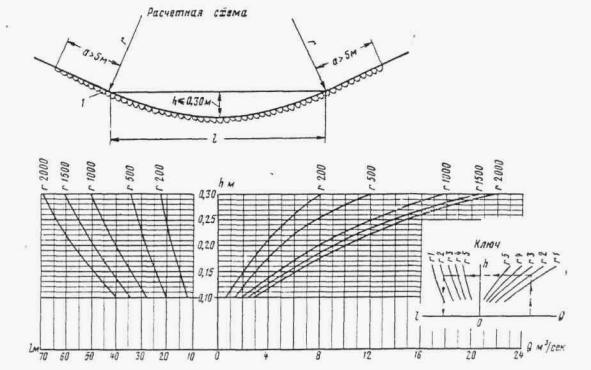
Рис. VIII .3. График гидравлического расчета бродов:
1 -одиночная мостовая или бетон.
Расчетные формулы:
1) ![]() ; 2)
; 2) ![]() ; 3) V = 3,1
; 3) V = 3,1 ![]() ; 4) Q = wv; 5) l = 1r sin
; 4) Q = wv; 5) l = 1r sin ![]()
4. Определяют среднюю скорость потока в м/сек в расчетном сечении по формуле
|
V = 3,1 |
( VIII.4) |
5. Определяют величину расхода в м3/сек:
Q = wv.
Если полученное значение отличается от заданного более чем на 10 %, расчет повторяют, принимая другие значения h или r или меняя и то, и другое.
Oпределение r, h и Q заканчивается, когда полученное значение будет отличаться от заданного Q paсч не более чем на 5 %.
6. Определяют ширину зеркала потока (длина хорды в м):
|
l = 2r sin |
( VIII.5) |
Брод и откосы насыпи в пределах брода обычно укрепляют мощением, реже бетоном. Укрепление производится на ширину l + 10 м, по 5 м в каждую сторону от концов расчетной ширины зеркала воды l.
На рис. VIII.3 приведен график для расчета бродов при глубине перелива от 0,1 до 0,3 м и дан ключ, показывающий порядок пользования графиком ля расчета бродов.
Пример. Определить элементы живого сечения брода через водоток с расходом Q = 15 м3/сек.
Задаемся радиусом r = 1000 м, тогда по правой части графика определяем глубину h = 0,28 м и по левой его части - длину брода l = 52 м.
ПРИЛОЖЕНИЯ
ПРИЛОЖЕНИЕ 1
ОСНОВНЫЕ ГИДРАВЛИЧЕСКИЕ ПОНЯТИЯ
Характеристика движения потока
1. Ламинарное движение - движение жидкости без пульсации скоростей и, следовательно, без перемешивания ее частиц.
2. Турбулентное движение - движение жидкости с пульсацией скоростей, приводящей к перемешиванию ее частиц.
3. Установившееся движение - движение жидкости, при котором ее скорость в любой точке живого сечения не изменяется во времени.
4. Равномерное движение - установившееся движение, при котором величина скорости частиц жидкости в соответственных точках живых сечений является одинаковой.
5. Неравномерное движение - движение жидкости, при котором величина скорости ее частиц в соответственных точках живых сечений не является одинаковой.
6. Плавно изменяющееся движение - неравномерное движение жидкости, при котором кривизна линий тока и угол расхождения между ними весьма малы и в пределе стремятся к нулю.
7. Безнапорное движение - движение жидкости с открытой поверхностью.
8. Напорное движение - движение жидкости, не имеющей свободной поверхности.
9. Спокойное состояние потока - состояние потока, при котором его глубина больше критической глубины.
10. Критическое состояние потока, при котором его глубины равны критической глубине.
11. Бурное состояние потока - состояние потока, при котором его глубины меньше критической глубины.
12. Свободное истечение - из отверстия в атмосферу, или истечение, не испытывающее сопротивления со стороны нижнего бьефа.
13. Несвободное истечение - истечение под уровень, или истечение, испытывающее сопротивление со стороны нижнего бьефа.
14. Сбойное течение - движение жидкости в массе затопленного прыжка воды, при котором узкая активная струя приобретает тенденцию сбиваться со своего направления.
15. Донный режим потока - условия движения жидкости, при которых наибольшие скорости наблюдаются у дна.
16. Поверхностный режим потока - условия движения жидкости, при которых наибольшие скорости наблюдаются у его свободной поверхности.
Основные параметры потока
17. Живое сечение - поверхность, проведенная в пределах потока жидкости, нормальная в каждой своей точке к вектору соответствующей местной скорости в этой точке.
18. Сжатое сечение потока - наименьшее живое сечение свободного потока, в котором движение жидкости можно рассматривать плавно изменяющимся.
19. Смоченный периметр - линия, по которой живое сечение соприкасается со стенками русла.
20. Гидравлический радиус - размерная величина, равная отношению площади живого сечения w к смоченному периметру c, т. е.
![]()
21. Расход потока - объем жидкости, протекающей в единицу времени через живое сечение.
22. Глубина - вертикальное расстояние в данном живом сечении безнапорного потока, измеряемое от свободной поверхности жидкости до наинизшей точки дна русла.
23. Бытовая глубина - глубина потока в естественном состоянии.
24. Нормальная глубина - глубина при равномерном движении жидкости в русле.
25. Критическая глубина - глубина, при которой заданный расход проходит с минимальным значением удельной энергии сечения.
26. Сжатая глубина - глубина в сжатом сечении потока.
27. Гидравлически наивыгоднейшее сечение - такая форма поперечного сечения русла, которая при заданных площади сечения и шероховатости дает наибольшую пропускную способность.
28. Подпор - глубина потока (больше бытовой), устанавливающаяся перед сооружением вследствие встречи потоком сопротивлений в сооружении; измеряется от низшей точки живого сечения перед сооружением до свободной поверхности.
29. Напор - сумма пьезометрического и скоростного напора.
30. Скоростной напор - высота, на которую может подняться над данной точкой жидкость, начавшая движение с вертикально направленной скоростью, при отсутствии сопротивлений ее движению.
Скорость потока
31. Средняя скорость потока - скорость, с которой должны были бы двигаться все частицы жидкости через данное живое сечение, чтобы сохранился расход, соответствующий действительному распределению скоростей в живом сечении.
32. Критическая скорость - величина средней скорости при критической глубине.
33. Местная скорость - средняя из мгновенных скоростей в данной точке потока, определенная за достаточно длительный промежуток времени.
Уклон потока
34. Геометрический уклон - падение дна русла на единицу его длины.
35. Гидравлический уклон - изменение удельной энергии потока, отнесенное к единице его длины.
36 Пьезометрический уклон - изменение удельной потенциальной энергии потока, отнесенное к единице его длины.
37. Критический уклон - уклон русла, при котором нормальная глубина равна критической глубине.
38. Уклон трения - см. гидравлический уклон.
Гидравлические сопротивления
39. а) Сопротивление по длине - сопротивление движению потока, вызываемое вязкостью и турбулентностью жидкости на участке рассматриваемой длины без учета влияния местных сопротивлений;
б) местные сопротивления - сопротивления движению потока, вызываемые каким-либо местным препятствием.
40. Коэффициент шероховатости - эмпирический коэффициент, учитывающий сопротивление трения жидкости о стенки и ложе русла.
41. Коэффициент гидравлических потерь - при равномерном движении (коэффициент Шези), учитывающий потери трения на границах потока.
42. Коэффициент Кориолиса - безразмерная величина, равная отношению кинетической энергии массы жидкости, протекающей в единицу времени через данное живое сечение, к кинетической энергии массы жидкости, вычисленной в предположении, что скорости во всех точках живого сечения равны средней скорости потока.
43. Коэффициент скорости - безразмерная величина, равная отношению средней скорости истечения данной жидкости из отверстия к средней скорости истечения невязкой жидкости из этого же отверстия.
44. Коэффициент сжатия струи - безразмерная величина, равная отношению площади сжатого сечения струи к площади отверстия.
45. Коэффициент расхода - безразмерная величина, равная отношению действительного расхода жидкости при истечении из отверстия к расходу невязкой жидкости из этого же отверстия при отсутствии сжатия.
46. Свободная поверхность жидкости - поверхность раздела между жидкостью и газообразной средой.
47. Кривая подпора - кривая свободной поверхности потока, в котором глубина возрастает в направлении движения жидкости.
48. Кривая спада - кривая свободной поверхности потока, в котором глубина убывает в направлении движения жидкости.
Бурный режим потока
49. Быстроток - искусственное русло с уклоном, большим критического, и с бурным режимом движения жидкости.
50. Гидравлический прыжок - переход из бурного состояния потока к спокойному, сопровождающийся резким переходом от глубин, меньших критической, к глубинам, большим критической, и от больших скоростей течения к меньшим.
51. Отогнанный прыжок - прыжок, расположенный на некотором расстоянии от падения струи.
52. Надвинутый прыжок - прыжок, образующийся непосредственно у сжатого сечения; высота прыжка равна глубине в нижнем бьефе.
53. Затопленный прыжок - прыжок, в котором сжатое сечение затопляется:
hсж = hбыт
54. Сопряженные глубины - глубины потока перед гидравлическим прыжком и за ним, характеризующиеся равенством их прыжковых функций.
55. Гидравлический водопад - переход из спокойного состояния потока в бурное, сопровождающийся резким изменением глубин (от больших критической к глубинам, меньше критической) и резким увеличением скоростей течения.
Гидравлические модели
56. Отверстие в тонкой стенке характеризуется истечением жидкости, при котором отсутствуют потери энергии по длине и в струе, образуется сжатое сечение; истечение из донного отверстия и истечение из-под щита являются разновидностью истечения через отверстие в тонкой стенке.
57. Отверстие в толстой стенке (насадка) характеризуется истечением жидкости, при котором вокруг сжатого сечения внутри насадки с острыми краями образуется область пониженного давления (вакуум); при закругленных краях насадки (коноидальная насадка) вакуума не образуется.
58. Водослив с острым порогом (тонкой стенкой). Горизонтальный порог, встречающийся на пути потока (при ширине вдоль потока S < 2/3 H), не оказывает влияния на форму переливающейся струи.
59. Водослив с широким порогом - горизонтальный порог (при ширине вдоль потока S > 2,5 H), на котором поток приобретает характер параллельно струйного течения с критической глубиной.
ПРИЛОЖЕНИЕ 2
ЗНАЧЕНИЕ БУКВ И РАЗМЕРНОСТЬ ВЕЛИЧИН, ВСТРЕЧАЮЩИХСЯ В РУКОВОДСТВЕ
hбыт - бытовая глубина в нижнем бьефе в м.
В - ширина потока в нестесненном состоянии, ширина разлива в м.
b - ширина водослива; отверстие искусственного сооружения; ширина канавы по дну в м.
С - коэффициент в уравнении равномерного движения (Шези).
D - внешний, больший диаметр; размер камня для мощения в м.
d - внутренний диаметр круглой трубы; глубина колодца в м.
F - площадь водосбора в км2.
G - масса вещества в кг.
g - ускорение силы тяжести, равное 9,81 м/сек2.
Н - подпор; высота насыпи; глубина канала; суммарный напор в уравнении Бернулли в м.
h - глубина воды в сооружении; hтр -высота трубы в свету; hf - потеря напора по длине;
h" - наибольшая сопряженная глубина в прыжке в м.
i - уклон дна; гидравлический уклон при равномерном движении; if - уклон трения.
К - модуль расхода в м3/сек; коэффициент фильтрации.
L - полная длина (сооружения) вдоль потока в м
l - частная длина вдоль потока; расстояние между сечениями в м
т - коэффициент откоса
п - число; коэффициент шероховатости; па - коэффициент шероховатости с учетом аэрации
Р - давление в кг/см2
р - высота порога в м.
Q - расход воды (потока) в м3/сек
q - удельный расход воды в м3/с e к
R - гидравлический радиус в м. r - радиус в м
Т - период времени
t - интервал времени в мин
v - средняя скорость течения в м/с e к
W - объем воды в м3
Z - высота над уровнем в уравнении Бернулли; глубина рисбермы; свободный напор при затопленном отверстии в м
Э - удельная энергия сечения
а - коэффициент неравномерности распределения скоростей по сечению (Кориолиса); для мостов а = 1,1, для труб а = 1
β - угол растекания потока; коэффициент; относительная ширина по дну
γ - вес единицы объема жидкости в кг/м3
∆ - приращение; доля величины
δ - соотношение масштабов; толщина стенки; величина, характеризующая устойчивость напорного режима
ε - коэффициент сжатия
θ - угол роспуска лотка
ξ - коэффициент местных гидравлических потерь
η - отношение глубин
λ- коэффициент гидравлического трения (Дарси); расстояние между ребрами шероховатости в м
μ - коэффициент расхода
а - коэффициент аэрации
j - коэффициент скорости
c - смоченный периметр
ψ - угол падения струи
Ώ - площадь в м2
w - площадь живого сечения в м2
ПРИЛОЖЕНИЕ 3
ОСНОВНЫЕ ГИДРАВЛИЧЕСКИЕ ФОРМУЛЫ
|
Зависимость, выражаемая формулой |
Формула |
|
Удельный расход |
|
|
Средняя скорость потока |
|
|
Гидравлический уклон |
|
|
Пьезометрический уклон для равномерного движения |
|
|
Гидравлический радиус |
|
|
Коэффициент С по Павловскому |
где
у = 2,5 ( |
|
Скорость течения при равномерном движении |
v = С |
|
Расходная характеристика |
|
|
Гидравлический показатель русла . |
|
|
Коэффициент сопротивления по длине |
|
|
Коэффициент сопротивления на входе |
ξвх = 0,505 + 0,303 sin θ + 0,226 sin2 θ |
|
Коэффициент сжатия. |
|
|
Коэффициент сопротивления на расширения |
|
|
Удельная энергия сечения |
|
|
Уравнение критического состояния потока |
|
|
Критический уклон |
|
|
Критическая глубина (в прямоугольном русле) |
|
|
Коэффициент расхода водослива с широким порогом |
|
|
Уравнение Бернулли (в практическом приложении в виде уравнения связи между смежными сечениями потока 1 и 2) |
|
|
Подпор перед трубой |
|
ПРИЛОЖЕНИЕ 4
ВРЕМЕННЫЕ НОРМЫ ДОПУСКАЕМЫХ СКОРОСТЕЙ ТЕЧЕНИЯ ВОДЫ В ПОСТОЯННЫХ ЕЛЕЗНОДОРОЖНЫХ ГИДРОТЕХНИЧЕСКИХ СООРУЖЕНИЯХ,
утвержденные МПС 12 декабря 1951 г.
Таблица I
Допускаемые (неразмывающие) средние скорости течения (в м/сек) для несвязных грунтов
|
Характеристика грунтов |
Размеры частиц грунтов в мм |
Средние глубины потока в м |
|||||
|
0,4 |
1,0 |
2,0 |
3,0 |
5,0 |
10,0 и более |
||
|
Средние скорости течения в м/сек |
|||||||
|
Пыль и ил с мелким песком; растительная земля |
0,005-0,05 |
0,15-0,20 |
0,20-0,30 |
0,25-0,40 |
0,30-0 45 |
0,40-0,55 |
0,45-0,65 |
|
Песок мелкий с примесью среднего |
0,05-0,25 |
0,20-0,35 |
0,30-0,45 |
0,40-0,55 |
0,45-0,60 |
0,55-0,70 |
0,65-0,80 |
|
» » » глиной; песок средний с примесью крупного |
0,25-1,00 |
0,35-0,50 |
0,45-0,60 |
0,55-0,70 |
0,60-0,75 |
0,70-0,85 |
0,80-0,95 |
|
Песок крупный с примесью гравия; среднезернистый песок с глиной |
1,00-2,50 |
0,50-0,65 |
0,60-0,75 |
0,70-0,80 |
0,75-0,90 |
0,85-1,00 |
0,95 - 1 ,20 |
|
Гравий мелкий с примесью среднего |
2,50-5,00 |
0,65-0,80 |
0,75-0,85 |
0,80-1,00 |
0,90-1,10 |
1,00-1,20 |
1,20- 1 ,50 |
|
Гравий крупный с песком н мелким гравием |
5,00-10,0 |
0,80-0,90 |
0,85-1,05 |
1,00-1 ,15 |
1,10-1,30 |
1,20-1,45 |
1,50-1,75 |
|
Галька мелкая с песком и гравием |
10,0-15,0 |
0,90-1,10 |
1,05-1,20 |
1,15-1,35 |
1,30-1,50 |
1,45-1,65 |
1,75-2,00 |
|
» средняя» » » » |
15,0-25,0 |
1,10-1,25 |
1,20-1,45 |
1,35-1,65 |
1,50-1,85 |
1,65-2,00 |
2,00-2,30 |
|
» крупная с примесью гравия |
25,0-40,0 |
1,25-1,50 |
1,45-1,85 |
1,65-2,10 |
1,85-2,30 |
2,00-2,45 |
2,30-2,70 |
|
Булыжник мелкий с галькой и гравием |
40,0-75,0 |
1,50-2,00 |
1,85-2,40 |
2,10-2,75 |
2,30-3,10 |
2,45-3,30 |
2,70-3,60 |
|
Булыжник средний с галькой |
75,0-100 |
2,00-2,45 |
2,40-2,80 |
2,75-3,20 |
3,10-3,50 |
3,30-3,80 |
3.60-4,20 |
|
» средний с примесью крупного; булыжник крупный с мелкими примесями |
100-150 |
2,45-3,00 |
2,80-3,35 |
3,20-3,75 |
3,50-4,10 |
3,80-4,40 |
4,20-4,50 |
|
Булыжник крупный с примесью мелких валунов и гальки |
150-200 |
3,00-3,50 |
3,35-3,80 |
3,75-4,30 |
4,10-4,65 |
4,40-5,00 |
1, 50-5,40 |
|
Валуны мелкие с примесью гальки |
200-300 |
3,50-3,85 |
3,80-4,35 |
4,30-4,70 |
4,65-4,90 |
5,00-5,50 |
5,40-5,90 |
|
» средние с примесью булыжника |
300-400 |
- |
4,35-4,75 |
4,70-4,95 |
4,90-5,30 |
5,50-5,60 |
5,90-6,00 |
|
» особо крупные |
400-500 и более |
- |
- |
4,95-5,35 |
5,30-5,50 |
5,60-6,00 |
6,00-6,20 |
Примечания . 1. В каждой графе таблицы нижние пределы скоростей течения соответствуют нижним пределам размеров частиц грунта, верхние пределы скоростей - верхним пределам размеров частиц.
2. Табличные значения скоростей не следует интерполировать. При промежуточных размерах частиц грунта и глубинах водотока значения скоростей течения принимаются по ближайшим табличным значениям размеров частиц и глубин водотока.
Таблица 2
ДОПУСКАЕМЫЕ (НЕРАЗМЫВАЮЩИЕ) СКОРОСТИ ТЕЧЕНИЯ ( в м/сек) ДЛЯ СВЯЗНЫХ ГРУНТОВ
|
Наименование грунтов |
Содержание частиц в % |
Грунты малоплотные (приведенная порозность 1,2 - 0.9), Объемный вес грунтового скелета до 1,20 т/м3 |
Грунты средпеплотные (приведенная порозность 0,9 - 0,6). Объемный вес грунтового скелета 1,20 - 1 ,66 т/м3 |
Грунты плотные (приведенная порозность 0,6-0,3). Объемный вес грунтового скелета 1,66 - 2,04 т/м3 |
Грунты очень плотные (приведенная порозность 0,3-0,2). Объемный вес грунтового скелета 2,04-2,14 т/м3 |
||||||||||||||||||
|
менее 0,005 мм |
0,005 - 0,05 мм |
||||||||||||||||||||||
|
Средние глубины потока в м |
|||||||||||||||||||||||
|
0,4 |
1,0 |
2,0 |
3,0 |
0,4 |
1,0 |
2,0 |
3,0 |
0,4 |
1,0 |
2,0 |
3,0 |
0,4 |
1,0 |
2,0 |
3,0 |
||||||||
|
Глины Тяжелые суглинки |
30-50 20-30 |
70-50 80-70 |
} 0,35 |
0,40 |
0,45 |
0,50 |
0,70 |
0,85 |
0,95 |
1,10 |
1,00 |
1,20 |
1,40 |
1,50 |
1,40 |
1,70 |
1,90 |
2,10 |
|||||
|
Тощие » |
10-20 |
90-80 |
0,35 |
0,40 |
0,45 |
0,50 |
0,65 |
0,80 |
0,90 |
1,00 |
0,95 |
1,20 |
1,40 |
1,50 |
1,40 |
1,70 |
1,90 |
2,10 |
|||||
|
Лёссовые грунты в условиях закончившихся просадок |
- |
- |
- |
- |
- |
- |
0,60 |
0,70 |
0,80 |
0,85 |
0,80 |
1,00 |
1,20 |
1,30 |
1,10 |
1,40 |
1,50 |
1,70 |
|||||
|
Супеси |
5-10 |
20-40 |
По табл. 1 в зависимости от крупности песчаных фракций |
||||||||||||||||||||
Примечания. 1. Табличные значения скоростей не следует интерполировать. При промежуточных глубинах водотока значения скоростей принимаются по глубинам, ближайшим к натурным.
2. Величины допускаемых скоростей течения при глубинах водотока, больших 3 м (в случае отсутствия специальных исследований и расчетов), прнимаются по их значениям для глубины 3 м.
3. При проектировании поверхностных водоотводов в подверженных выветриванию плотных и очень плотных грунтах допускаемые скорости ограничиваются теми же значениями, что и для грунтов средней плотности (по графам 9, 10, II и 12)
Таблица 3
ДОПУСКАЕМЫЕ (НЕРАЗМЫВАЮЩИЕ) СРЕДНИЕ СКОРОСТИ ТЕЧЕНИЯ ( в м/сек)
ДЛЯ ИСКУССТВЕННЫХ УКРЕПЛЕНИЙ
|
Тип укреплений |
Средние глубины потока в м |
|||
|
0,4 |
1,0 |
2,0 |
3,0 |
|
|
Одерновка плашмя (на плотном основании) |
0.9 |
1,2 |
1,3 |
1,4 |
|
Одерновка в стенку |
1,5 |
1,8 |
2,0 |
2,2 |
|
Каменная наброска из булыжного или рваного камня в зависимости от его крупности |
По табл. 1 с коэффициентом 0,90 |
|||
|
Каменная наброска в два слоя в плетнях в зависимости от крупности камня |
По табл. 1 с коэффициентом 1,10 |
|||
|
Одиночное мощение на мху (слой мха не менее 5 см): |
|
|
|
|
|
а) Из булыжника размером 15 см |
2,0 |
2,5 |
3,0 |
3,5 |
|
б) » » » 20 » |
2,5 |
3,0 |
3,5 |
4,0 |
|
в) » » » 25 » |
3,0 |
3,5 |
4,0 |
4,5 |
|
Одиночное мощение на щебне (слой щебня не менее 10 см: |
|
|
|
|
|
а) из рваного камня размером 15 см |
2,5 |
3,0 |
3,5 |
4,0 |
|
б) » » » 20 » |
3,0 |
3,5 |
4,0 |
4.5 |
|
в) » » » 25 » |
3,5 |
4,0 |
4,5 |
5,0 |
|
Одиночное мощение с подбором лица и грубым приколом на щебне (слон щебня не менее 10 см): |
|
|
|
|
|
а) из камней размером 20 см |
3,5 |
4,5 |
5,0 |
5,5 |
|
б) » » » 25 » |
4,0 |
4,5 |
5,5 |
5,5 |
|
в) » » » 30» |
4,0 |
5,0 |
6,0 |
6,0 |
|
Двойное мощение из рваного камня на щебне: |
|
|
|
|
|
нижний слой из камней 15 см, верхний - из камней 20 см (слой щебня не менее 10 см) |
3,5 |
4,5 |
5,0 |
5,5 |
|
Хворостяная выстилка и хворостяные покрывала на плотном основании (для временных укреплений): |
|
|
|
|
|
а) при толщине выстилки 3 = 20 - 25 см |
- |
2,0 |
2,5 |
- |
|
б) при других толщинах выстилки |
По п. а с коэффициентом |
|||
|
Фашинные тюфяки: |
|
|
|
|
|
а) При толщине δ = 50 см |
2,5 |
3,0 |
3,5 |
- |
|
б) При других толщинах тюфяков |
По п. а с коэффициентом |
|||
|
Габионы (размерами не менее 0,5×0,5×1,0) |
До 4,0 |
До 5,0 |
До 5,5 |
До 6,0 |
|
Бутовая кладка из камня известковых пород (с пределом прочности не менее. 100 кг/см2) |
3,0 |
3,5 |
4,0 |
4,5 |
|
Бутовая кладка из камня крепких пород (с пределом прочности не менее 300 кг/см2) |
6,5 |
8,0 |
10,0 |
12,0 |
|
Бетон как одежда для креплений: |
|
|
|
|
|
Марки 170 |
6,5 |
8,0 |
9,0 |
10 |
|
» 140 |
6,0 |
7,0 |
8,0 |
9,0 |
|
» 110 |
5,0 |
6,0 |
7,0 |
7,5 |
|
Бетонные лотки с гладкой поверхностью: |
|
|
|
|
|
Бетон марки 170 |
13 |
16 |
19 |
20 |
|
» » 140 |
12 |
14 |
16 |
18 |
|
» » 110 |
10 |
12 |
13 |
15 |
|
Деревянные лотки гладкие при надежном основании и течении вдоль волокон |
8 |
10 |
12 |
14 |
Примечания. 1. Табличные значения скоростей не следует интерполировать. При промежуточных глубинах водотока значения скоростей принимаются по глубинам, ближайшим к натурным.
2. Величины допускаемых скоростей течения при глубинах водотока, больших 3 м (в случае отсутствия специальных исследований и расчетов), принимаются по их значениям для глубины 3 м.
ПРИЛОЖЕНИЕ 5
КОЭФФИЦИЕНТЫ ГИДРАВЛИЧЕСКОЙ ШЕРОХОВАТОСТИ n К ФОРМУЛАМ ПАВЛОВСКОГО
|
Характер поверхности русла |
Состояние поверхности |
|||
|
очень хорошее |
хорошее |
обычное |
плохое |
|
|
Лотки и трубы |
|
|
|
|
|
Деревянные лотки |
0,010 |
0,011 |
0,012 |
0,014 |
|
Цементная штукатурка |
0,011 |
0,012 |
0,013 |
|
|
Шпальные лотки ... |
- |
0,013 |
0,016 |
0,018 |
|
Гладкая бетонная поверхность, тесовая кладка |
0,012 |
0,014 |
0,015 |
0,016 |
|
Шероховатая бетонная поверхность |
- |
0,014 |
0,016 |
0,018 |
|
Бетонировка цемент-пушкой |
0,016 |
0,019 |
0,021 |
- |
|
Бутовая кладка, грубая бетонировка |
0,017 |
0,020 |
0,025 |
0,030 |
|
Грубая бутовая кладка |
0,020 |
0,025 |
0,027 |
0,030 |
|
Сухая кладка |
0,025 |
0,030 |
0,035 |
0,038 |
|
Канавы и искусственные русла |
|
|
|
|
|
Земляные канавы правильной формы в плотном лёссе пли мелком гравии с илистым слоем |
- |
0,017 |
0,018 |
- |
|
То же в лёссе или гравии с илистой пленкой |
0,017 |
0,020 |
0,020 |
0,025 |
|
То же с замощенным контуром, мощение обычным булыжным камнем одиночное или двойное |
- |
0,020 |
0,022 |
0,027 |
|
То же мощение из крупного камня |
0,017 |
0,022 |
0,023 |
0,030 |
|
То же искусственная габионная кладка |
- |
0,025 |
0,027 |
0,029 |
|
Канавы в галечнике |
0,025 |
0,027 |
0,030 |
0,033 |
|
Земляные канавы неправильной формы (с обвалами) заросшие, каменная наброска или мощение из рваного камня |
- |
0,027 |
0,030 0,033 |
0,035 |
|
Канавы с земляным дном и одернованными или сложенными сухой кладкой откосами |
0,028 |
0,030 |
0,33 |
0,035 |
|
Канавы с одернованными откосами и мощеным дном или грубо высеченным в скале (неправильной формы) . |
0,025 |
0,030 |
0,035 |
0,040 |
|
Мощение с «изюмом» |
- |
- |
0,04 |
0,045 |
|
Чешуйчатые покрытия |
- |
- |
0,06 |
- |
|
Естественные русла |
|
|
|
|
|
Естественные русла в весьма благоприятных условиях (чистое, прямое, незасоренное земляное со свободным течением русло) |
0,025 |
- |
- |
- |
|
Русла постоянных водотоков равнинного типа (преимущественно больших и средних рек) при благоприятном состоянии их ложа и течения воды. Периодические потоки (большие и малые) при очень хорошем состоянии поверхности и формы ложа |
0,033 |
|
|
|
|
Сравнительно чистые русла постоянных равнинных водотоков в обычных условиях, извилистые с некоторыми неправильностями в направлении струй или же прямые, но с неправильностями в рельефе дна (отмели, промоины, местами камни). Земляные русла периодических водотоков(сухих лотков) в относительно |
|
0,040 |
|
|
|
Русла (больших и средних рек) значительно засоренные, извилистые и частично заросшие, каменистые с неспокойным течением. Периодические (ливневые и весенние) водотоки, несущие во время паводка заметное количество наносов с крупногалечным или покрытым растительностью (травой и пр.) ложем. Поймы больших и средних рек, сравнительно разработанные, покрытые нормальным количеством |
|
|
0,050 |
|
|
Русла периодических водотоков сильно засоренные и извилистые. Сравнительно заросшие, неровные, плохо разработанные поймы рек (промоины, кустарники, деревья с наличием заводей). Галечно-валунные русла горного типа с неправильной поверхностью водного зеркала. Порожистые участки равнинных рек |
|
|
|
0,067 |
|
Реки и поймы, весьма значительно заросшие (со слабым течением) с большими глубокими промоинами. Валунные, горного типа русла с бурливым пенистым течением, с изрытой поверхностью водного зеркала (с летящими вверх брызгами воды) |
|
|
|
0,080 |
|
Поймы такие же, как предыдущей категории, но с сильно неправильным течением, заводями и пр. Горноводопадного типа русла с крупновалунным извилистым строением ложа, перекаты ярко выражены, пенистость настолько сильна, что вода, потеряв прозрачность, имеет белый цвет, шум потока доминирует над всеми остальными звуками, делает разговор затруднительным |
|
|
|
0,100 |
|
Характеристика горных рек примерно та же, что и предыдущей категории. Реки болотного типа (заросли, кочки, во многих местах почти стоячая вода и пр.). Поймы с очень большими мертвыми пространствами, с местными углублениями, озерами и пр. |
|
|
|
0,133 |
|
Потоки типа селевых, состоящие из грязи, камней и пр. Глухие поймы (сплошь лесные, таежного типа) |
- |
- |
- |
0,200 |
Примечания. 1. Характеристики состояния поверхности относятся как к обработке материала поверхности, так и к состоянию поверхности. Так, например, для деревянного лотка состояние: очень хорошее характеризует строганые доски, обычное - нестроганые доски, плохое - нестроганые доски со щелями, выступами, загрязненные при частично занесенном наносами лотке.
2. Коэффициенты шероховатости для естественных русел приняты по классификации проф. Срибного.
ПРИЛОЖЕНИЕ 6
ЗНАЧЕНИЯ КОЭФФИЦИЕНТА С ПО ФОРМУЛЕ ПАВЛОВСКОГО
![]()
|
R в м |
п |
|||||||
|
0,011 |
0,013 |
0,017 |
0,020 |
0,025 |
0,030 |
0,035 |
0,040 |
|
|
0,05 |
61,3 |
48,7 |
33,2 |
26,1 |
18,6 |
13,9 |
10,9 |
8,7 |
|
0,06 |
62,8 |
50,1 |
34,4 |
27,2 |
19,5 |
14,7 |
11,5 |
9,3 |
|
0,07 |
64,1 |
51,3 |
35,5 |
28,2 |
20,4 |
15,5 |
12,2 |
9,9 |
|
0,08 |
65,2 |
52,4 |
36,4 |
29,0 |
21,1 |
16,1 |
12,8 |
10,3 |
|
0,10 |
67,2 |
54,3 |
38,1 |
30,6 |
22,4 |
17,3 |
13,8 |
11,2 |
|
0,12 |
68,8 |
55,8 |
39,5 |
32,0 |
23,5 |
18,3 |
14,7 |
12,1 |
|
0,14 |
70,3 |
57,2 |
40,7 |
33,0 |
24,5 |
19,1 |
15,4 |
12,8 |
|
0,16 |
71,5 |
58,4 |
41,8 |
34,0 |
25,4 |
19,9 |
16,1 |
13,4 |
|
0,18 |
72,6 |
59,5 |
42,7 |
34,8 |
26,2 |
20,6 |
16,8 |
14,0 |
|
0,20 |
73 7 |
60,4 |
43,6 |
35,7 |
26,9 |
21,3 |
17,4 |
14,5 |
|
0,22 |
74,6 |
61,3 |
44,4 |
36,4 |
27,6 |
21,9 |
17,9 |
15,0 |
|
0,24 |
75,5 |
62,1 |
45,2 |
37,1 |
28,3 |
22,5 |
18,5 |
15,5 |
|
0,26 |
76,3 |
62,9 |
45,9 |
37,8 |
28,8 |
23,0 |
18,9 |
16,0 |
|
0,28 |
77,0 |
63,6 |
46,5 |
38,4 |
29,4 |
23,5 |
19,4 |
16,4 |
|
0,30 |
77,7 |
64,3 |
47,2 |
39,0 |
29,9 |
24,0 |
19,9 |
16,8 |
|
0,35 |
79,3 |
65,8 |
48,6 |
40,3 |
31,1 |
25,1 |
20,9 |
17,8 |
|
0,40 |
80,7 |
67,1 |
49,8 |
41,5 |
32,2 |
26,0 |
21,8 |
18,6 |
|
0,45 |
82,0 |
68,4 |
50,9 |
42,5 |
33,1 |
26,9 |
22,6 |
19,4 |
|
0,50 |
83,1 |
69,5 |
51,9 |
43,5 |
34,0 |
27,8 |
23,4 |
20,1 |
|
0,55 |
84,1 |
70,4 |
52,8 |
44,4 |
34,8 |
28,5 |
24,0 |
20,7 |
|
0,60 |
85,3 |
71,4 |
53,7 |
45,2 |
35,5 |
29,2 |
24,7 |
21,3 |
|
0.65 |
86,0 |
72,2 |
54,5 |
45,9 |
36,2 |
29,8 |
25,3 |
21,9 |
|
0,70 |
86,8 |
73,0 |
55,2 |
46,6 |
36,9 |
30,4 |
25,8 |
22,4 |
|
0,80 |
88,3 |
74,5 |
56,5 |
47,9 |
38,0 |
31,5 |
26,8 |
23,4 |
|
0,90 |
89,4 |
75,5 |
57,5 |
48,8 |
38,9 |
32,3 |
27,6 |
24,1 |
|
1,00 |
90,9 |
76,9 |
58,8 |
50,0 |
40,0 |
33,3 |
28,6 |
25,0 |
|
1,10 |
92,0 |
78,0 |
59,8 |
50,9 |
40,9 |
34,1 |
29,3 |
25,7 |
|
1,20 |
93,1 |
79,0 |
60,7 |
51,8 |
41,6 |
34,8 |
30,0 |
26,3 |
|
1,30 |
94,0 |
79,9 |
61, b |
52,5 |
42,3 |
35,5 |
30,6 |
26,9 |
|
1,50 |
95,7 |
81,5 |
62,9 |
53,9 |
43,6 |
36,7 |
31,7 |
28,0 |
|
1,70 |
97,3 |
82,9 |
64,3 |
55,1 |
44,7 |
37,7 |
32,7 |
28,9 |
|
2,00 |
99,3 |
84,8 |
65,9 |
56,6 |
46,0 |
38,9 |
33,8 |
30,0 |
|
2,50 |
102,1 |
87,3 |
68,1 |
58,7 |
47,9 |
40,6 |
35,4 |
31,5 |
|
3,00 |
104,4 |
89,4 |
69,8 |
60,3 |
49,3 |
41,9 |
36,6 |
32,5 |
|
3,50 |
106,4 |
91,1 |
71,3 |
62,5 |
50,3 |
42,8 |
37,4 |
33,3 |
|
4,00 |
108,1 |
92,6 |
72,5 |
62,5 |
51,2 |
43,6 |
38,1 |
33,9 |
|
5,00 |
111,0 |
95,1 |
74,2 |
64,1 |
52,4 |
44,6 |
38,9 |
34,6 |
ПРИЛОЖЕНИЕ 7
График коэффициента С по формуле Павловского
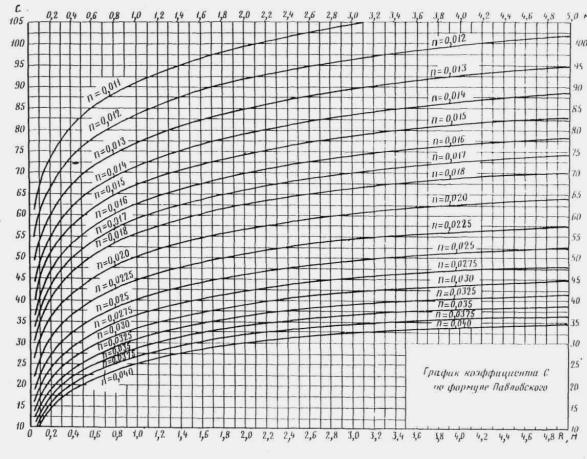
ПРИЛОЖЕНИЕ 8
График для определения глубины воды при равномерном движении в прямоугольном русле ( п = 0,016)
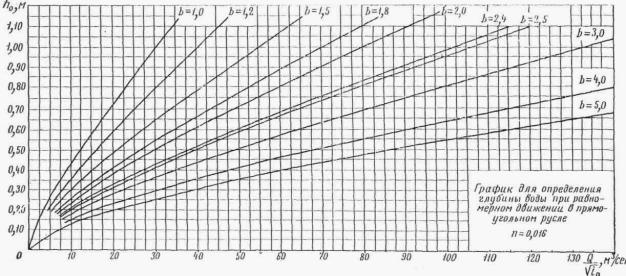
График составлен по формуле Q = wС ![]()
Пример: Дано- Q = 9 м3/сек; i0 = 0,20; b = 2 м; п = 0,016.
Вычисляем ![]() ; по графику h0 =
0,37 м
; по графику h0 =
0,37 м
ПРИЛОЖЕНИЕ 9
График для определения критической глубины потока и полного напора на водосливе в русле прямоугольного сечения
График составлен по формуле
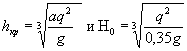
Пример: Дано - Q = 9 м3/сек; b = 2 м g = 9/2 = 4,5 м2/сек.
По графику hкр = 1,275 м.
ПРИЛОЖЕНИЕ 10
График для определения расчетной длины кривой спада в призматическом русле прямоугольного сечения
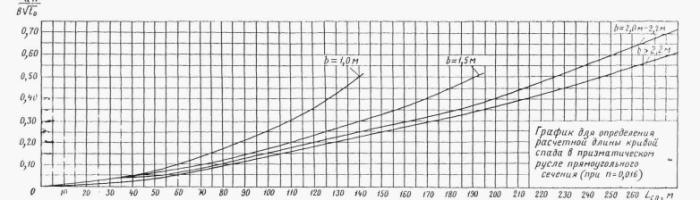
График составлен по уравнению Черноморского
II ример: Дано - Q = 9 м3/сек; b = 2 м; i0 = 0.20; n = 0,016
Вычисляем ![]() ; по графику Lсп = 113 м.
; по графику Lсп = 113 м.
ПРИЛОЖЕНИЕ 11
График для построения кривой свободной поверхности в призматическом русле.( n = 0,016)
Пример: Дано - Q = 9 м3/сек; b = 2 м; i0 = 0,20; n = 0,016
Определены - по прил. 8 h0 = 0,37; по прил. 9 hкр = 1,275 м по прил. 10 Lсп = 113 требуется построить кривую свободной поверхности потока на длине быстротока 20 м
ПРИЛОЖЕНИЕ 12
ГИДРАВЛИЧЕСКИЕ КОЭФФИЦИЕНТЫ
Таблица 1
Коэффициенты для входных оголовков труб при безнапорном режиме
|
Тип входного оголовка |
Коэффициент сжатия ε |
Коэффициент скорости j |
|
Обтекаемый |
1,00 |
0,97 |
|
Раструбный |
0,90 |
0,98 |
|
Портальный |
0,85 |
0,98 |
Таблица 2
Коэффициенты для входных оголовков труб при полунапорном режиме
|
Тип входного оголовка |
Коэффициент сжатия |
|||
|
По сечению ε w |
По вертикали ε h |
Коэффициент скорости j |
||
|
для прямоугольного сечения |
для круглого сечения |
|||
|
Раструбный |
0,64 |
0,64 |
0,60 |
0,97 |
|
Портальный |
0,62 |
0,60 |
0,60 |
0,95 |
|
Обтекаемый |
0,65 |
0,65 |
0,60 |
0,95 |
Таблица 3
Коэффициенты для входных оголовков труб при напорном режиме
|
Тип входного оголовка |
Коэффициент сжатия ε |
Коэффициент скорости j |
|
Обтекаемый |
1,00 |
0,97 |
|
Раструбный |
0,62 |
0,83 |
|
Портальный |
0,62 |
0,83 |
Таблица 4
Коэффициенты для однопролетных мостов
|
Форма устоев |
Коэффициент сжатия ε |
Коэффициент скорости j |
|
Обтекаемые с конусами |
0,90 |
0,90 |
|
С откосными крыльями |
0,85 |
0,90 |
|
Выступающие из конуса |
0,80 |
0,85 |
ПРИЛОЖЕНИЕ 13
ПЛОЩАДЬ ЖИВОГО СЕЧЕНИЯ Kw И ГИДРАВЛИЧЕСКИЙ РАДИУС KR ЧАСТИЧНО НАПОЛНЕННЫХ КРУГЛЫХ ТРУБ (ПРИ D = 1)
|
|
Коэффициенты |
0,00 |
0,01 |
0,02 |
0,03 |
0,04 |
0,05 |
0,06 |
0,07 |
0,08 |
0,09 |
|
0,0 |
Kw |
0,000 |
0,001 |
0,004 |
0,007 |
0,010 |
0,015 |
0,019 |
0,024 |
0,029 |
0,035 |
|
KR |
0,000 |
0,007 |
0,013 |
0,020 |
0,026 |
0,033 |
0,039 |
0,045 |
0,051 |
0,057 |
|
|
0,1 |
Kw |
0,041 |
0,047 |
0,053 |
0,060 |
0,067 |
0,073 |
0,081 |
0,088 |
0,096 |
0,104 |
|
KR |
0,063 |
0,070 |
0,075 |
0,081 |
0,087 |
0,093 |
0,099 |
0,104 |
0,110 |
0,115 |
|
|
0,2 |
Kw |
0,112 |
0,120 |
0,128 |
0,137 |
0,145 |
0,153 |
0,162 |
0,171 |
0,180 |
0,189 |
|
KR |
0,121 |
0,126 |
0,131 |
0,136 |
0,142 |
0,147 |
0,152 |
0,157 |
0,161 |
0,166 |
|
|
0,3 |
Kw |
0,198 |
0,207 |
0,217 |
0,226 |
0,235 |
0,245 |
0,255 |
0,264 |
0,274 |
0,284 |
|
KR |
0,171 |
0,176 |
0,180 |
0,185 |
0,189 |
0,193 |
0,198 |
0,202 |
0,206 |
0,210 |
|
|
0,4 |
Kw |
0,293 |
0,303 |
0,313 |
0,323 |
0,333 |
0,343 |
0,352 |
0,362 |
0,373 |
0,383 |
|
KR |
0,214 |
0,218 |
0,222 |
0,226 |
0,229 |
0,233 |
0,236 |
0,240 |
0,243 |
0,247 |
|
|
0,5 |
Kw |
0,393 |
0,403 |
0,413 |
0,423 |
0,433 |
0,443 |
0,453 |
0,462 |
0,472 |
0,482 |
|
KR |
0,250 |
0,253 |
0,256 |
0,259 |
0,262 |
0,265 |
0,268 |
0,270 |
0,273 |
0,275 |
|
|
0,6 |
Kw |
0,492 |
0,502 |
0,512 |
0,521 |
0,531 |
0,540 |
0,550 |
0,559 |
0,569 |
0,578 |
|
KR |
0,278 |
0,280 |
0,282 |
0,284 |
0,286 |
0,288 |
0,290 |
0,292 |
0,293 |
0,295 |
|
|
0,7 |
Kw |
0,587 |
0,596 |
0,605 |
0,614 |
0,623 |
0,632 |
0,640 |
0,649 |
0,657 |
0,666 |
|
KR |
0,296 |
0,298 |
0,299 |
0,300 |
0,301 |
0,302 |
0,302 |
0,303 |
0,304 |
0,304 |
|
|
0,8 |
Kw |
0,674 |
0,681 |
0,689 |
0,697 |
0,704 |
0,712 |
0,719 |
0,725 |
0,732 |
0,738 |
|
KR |
0,304 |
0,304 |
0,304 |
0,304 |
0,304 |
0,303 |
0,303 |
0,302 |
0,301 |
0,299 |
|
|
0,9 |
Kw |
0,745 |
0,750 |
0,756 |
0,761 |
0,766 |
0,771 |
0,775 |
0,779 |
0,782 |
0,784 |
|
KR |
0,298 |
0,296 |
0,294 |
0,292 |
0,289 |
0,286 |
0,283 |
0,279 |
0,274 |
0,267 |
Для определения площади живого сечения для заданного D имеем
w = Kw D2
Для определения гидравлического радиуса соответственно имеем
R = KR D.
Пример.
D = 2 м; h = 1,5 м.
Определить w и R.
1) ![]() ; 2) по таблице Kw = 0,632; KR =
0,302; 3) w = 0,632·22 = 2,528 м2;
; 2) по таблице Kw = 0,632; KR =
0,302; 3) w = 0,632·22 = 2,528 м2;
4) R = 0,302·2 = 0,604 м.
ПРИЛОЖЕНИЕ 14
ПРОПУСКНАЯ СПОСОБНОСТЬ КРУГЛЫХ ТРУБ
|
Q в м3/сек |
d тр = 1,0 |
d тр = 1,25 |
d тр = 1,50 |
d тр = 2,00 |
Q в м3/сек |
||||||||||||
|
I |
II |
I |
II |
I |
II |
I |
II |
||||||||||
|
H |
V |
H |
V |
H |
V |
H |
V |
H |
V |
H |
V |
H |
V |
H |
V |
||
|
0,8 |
0,82 |
2,0 |
6,76 |
2,0 |
0,73 |
1,8 |
0,67 |
1,8 |
0,69 |
1,8 |
0,64 |
1,8 |
0,67 |
1,7 |
0,61 |
1,7 |
0,8 |
|
0,9 |
0,88 |
2,0 |
0,81 |
2,0 |
0,76 |
1,9 |
0,71 |
1,9 |
0,74 |
1.8 |
0,68 |
1,8 |
0,69 |
1,8 |
0,65 |
1,8 |
0,9 |
|
1,0 |
0,94 |
2,1 |
0,86 |
2,1 |
0,82 |
1,9 |
0,75 |
1,9 |
0,78 |
1,9 |
0,72 |
1,9 |
0,73 |
1,8 |
0,68 |
1,8 |
1,0 |
|
1.1 |
1,00 |
2,2 |
0,91 |
2,2 |
0,86 |
2,0 |
0,79 |
2,0 |
0,82 |
1,9 |
0,76 |
1,9 |
0,77 |
1,9 |
0,72 |
1,0 |
1,1 |
|
1.2 |
1,06 |
2,3 |
0,96 |
2,3 |
0,91 |
2,1 |
0,84 |
2,1 |
0,87 |
2,0 |
0,80 |
2,0 |
0,81 |
1,9 |
0,75 |
1,9 |
1.2 |
|
1,4 |
1,17 |
2,5 |
1,06 |
2,5 |
1,00 |
2,2 |
0,92 |
2,2 |
0,93 |
2,1 |
0,87 |
2,1 |
0,89 |
2,0 |
0,82 |
2,0 |
1,1 |
|
1,6 |
1,37 |
3,4 |
1,14 |
2,6 |
1,09 |
2,3 |
1,00 |
2,3 |
1,00 |
2,2 |
0,93 |
2,2 |
0,93 |
2,1 |
0,87 |
2,1 |
1,0 |
|
1,8 |
1,69 |
3,7 |
1,23 |
2,6 |
1,16 |
2,4 |
1,07 |
2,4 |
1,08 |
2,2 |
1,00 |
2,2 |
0,99 |
2,1 |
0,92 |
2,1 |
1, 8 |
|
2,0 |
1,80 |
4,1 |
1,32 |
2,7 |
1,26 |
2,5 |
1,13 |
2,5 |
1,15 |
2,3 |
1,07 |
2,3 |
1,05 |
2,2 |
0,97 |
2,2 |
2, 0 |
|
2,2 |
2,04 |
4,6 |
1,47 |
2,8 |
1,33 |
2,6 |
1,21 |
2,6 |
1,21 |
2,4 |
1,12 |
2,4 |
1,11 |
2,2 |
1,02 |
2,2 |
2,2 |
|
2,5 |
2,47 |
5,1 |
1,58 |
3,2 |
1,43 |
2,8 |
1,31 |
2,8 |
1,30 |
2,5 |
1,20 |
2,5 |
1,19 |
2,3 |
1,10 |
2,3 |
2, 5 |
|
3,0 |
3,26 |
6,2 |
1,82 |
3,8 |
1,86 |
3,8 |
1,45 |
2,9 |
1,47 |
2.7 |
1,33 |
2,7 |
1,30 |
2,4 |
1,21 |
2,4 |
3,1 |
|
3,5 |
4,20 |
7,2 |
2,14 |
4,5 |
2,24 |
4,6 |
1,60 |
3,1 |
1,63 |
2,9 |
1,48 |
2,9 |
1,41 |
2,6 |
1,31 |
2,6 |
3,5 |
|
4,0 |
5,20 |
8,1 |
2,47 |
5,1 |
2,66 |
5,2 |
1,84 |
3,2 |
1,75 |
3,1 |
1,60 |
3,1 |
1,53 |
2,7 |
1,43 |
2,7 |
4,0 |
|
4,5 |
- |
- |
2,87 |
5,7 |
3,26 |
5,9 |
1,98 |
3,7 |
2,07 |
4,2 |
1,71 |
3,2 |
1,65 |
2,8 |
1,53 |
2,8 |
4.5, |
|
5,0 |
- |
- |
3,27 |
6,3 |
3,70 |
6.5 |
2,17 |
4,0 |
2,38 |
4,6 |
1,83 |
3,3 |
1,75 |
2.9 |
1,61 |
2,9 |
5,0 |
|
5,5 |
- |
- |
3,76 |
6,97, |
4,25 |
7,2 |
2,37 |
4,5 |
2,67 |
5,0 |
1,95 |
3,4 |
1,86 |
3,0 |
1,71 |
3.0 |
5,5 |
|
6,0 |
- |
- |
4,27 |
7,6 |
5,00 |
7,8 |
2,58 |
4,8 |
2,99 |
5,5 |
2,09 |
3,6 |
1,97 |
3,1 |
1,79 |
3,1 |
6,0 |
|
6,5 |
- |
- |
4,84 |
8,2 |
5,50 |
8,8 |
2,82 |
5,2 |
3,32 |
5,9 |
2,27 |
3,7 |
2,06 |
3,2 |
1,88 |
3,2 |
0,5 |
|
7,0 |
- |
- |
5,45 |
8,9 |
6,20 |
9,5 |
3,09 |
5,7 |
3,77 |
6,3 |
2.40 |
4,0 |
2,16 |
3,3 |
1,97 |
3,3 |
7,0 |
|
7,5 |
- |
- |
6,10 |
9,5 |
6,80 |
10 |
3,34 |
6,1 |
4,16 |
6,8 |
2,52 |
4,2 |
2,26 |
3,4 |
2,07 |
3,4 |
7,5 |
|
8,0 |
- |
- |
6,80 |
10 |
7,50 |
11 |
3,64 |
6,4 |
4,54 |
7,2 |
2,64 |
4,5 |
2,34 |
3,6 |
2,08 |
3,6 |
8,0 |
|
8,5 |
|
|
7,55 |
11 |
- |
- |
3,91 |
6,8 |
5,09 |
7,7 |
2,79 |
4,8 |
2,38 |
3,6 |
2,18 |
3,6 |
8,5 |
|
9,0 |
- |
- |
|
|
- |
- |
4,22 |
7,2 |
5,60 |
8,2 |
2,93 |
5,1 |
2,66 |
4,6 |
2,29 |
3,7 |
9,0 |
|
9,5 |
- |
- |
9,39 |
12 |
- |
- |
4,68 |
7,7 |
6,07 |
8,6 |
3,10 |
5,4 |
2,86 |
4,9 |
2,36 |
3, 7 |
9,5 |
|
10 |
- |
- |
10,70 |
13 |
- |
- |
4,98 |
8,2 |
6,42 |
9,7 |
3,29 |
5,6 |
3,07 |
5,1 |
2,44 |
3,8 |
10 |
|
11 |
- |
- |
12,00 |
14 |
- |
- |
5.76 |
9,0 |
7,26 |
11 |
3,68 |
6,2 |
3,46 |
5,6 |
2,62 |
3,9 |
11 |
|
12 |
- |
- |
- |
- |
- |
- |
6,60 |
9,8 |
- |
- |
4,12 |
6,8 |
3,83 |
6,1 |
2,74 |
4,0 |
12 |
|
13 |
- |
- |
- |
- |
- |
- |
7,55 |
10 |
- |
- |
4,52 |
7,3 |
4,25 |
6,6 |
2,96 |
4,1 |
13 |
|
14 |
- |
- |
- |
- |
- |
|
8,55 |
11 |
- |
- |
4,99 |
7,9 |
4,76 |
7,1 |
3,10 |
1,4 |
11 |
|
15 |
- |
- |
- |
- |
- |
- |
9,63 |
12 |
- |
- |
5,51 |
8,4 |
5,29 |
7,6 |
3,28 |
4,7 |
15 |
|
16 |
- |
- |
- |
- |
- |
- |
10,80 |
13 |
- |
- |
6,06 |
9,0 |
5,82 |
8,1 |
3,40 |
5,0 |
1Ь |
|
17 |
- |
- |
- |
- |
- |
- |
11,90 |
14 |
- |
- |
6,70 |
9,6 |
6,47 |
8,7 |
3,60 |
5,4. |
17 |
|
18 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
7,33 |
10 |
7,08 |
9,2 |
3,80 |
5,7 |
18 |
|
19 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
8,00 |
11 |
7,81 |
9,8 |
4,04 |
6,0 |
19 |
|
20 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
8,70 |
11 |
8,40 |
11 |
4,27 |
6,4 |
20 |
|
21 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
9,44 |
12 |
9,16 |
12 |
4,60 |
6,7 |
21 |
|
22 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
10,2 |
12 |
9,94 |
12 |
4.74 |
7,0 |
22 |
|
23 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
11,0 |
13 |
10,7 |
13 |
1,98 |
7,2 |
23 |
|
24 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
11,8 |
14 |
11,5 |
13 |
5.28 |
7,6 |
24 |
Примечания. 1. Римскими цифрами обозначены типы оголовков труб: I - раструбные, II - обтекаемые. При портальных и воротниковых оголовках расход при том же Н уменьшается на 10 %.
2. Выше черты все данные применяются для расчета при безнапорном режиме с запасом на выходе % высоты трубы, но не более 0,25 м; ниже черты-при чрезвычайных условиях эксплуатации.
ПРИЛОЖЕНИЕ 15
ГИДРАВЛИЧЕСКИЕ ХАРАКТЕРИСТИКИ ТИПОВЫХ КРУГЛЫХ ЖЕЛЕЗОБЕТОННЫХ ТРУБ
Таблица 15.1
Трубы под железную дорогу
(инв. № 121/2)
|
Тип оголовка |
Отверстие в м |
Безнапорный режим |
Напорный режим |
||||||||||
|
Qp в м3/сек |
Q макс в м3/сек |
H в м |
H вх в м |
H к в м |
H кр в м |
h сж в м |
i кр |
v вых в м/сек |
Q макс в м3/сек |
H в м |
v вых в м/сек |
||
|
Раструбный оголовок с коническим входным звеном |
1,00 |
0,50 |
|
0,57 |
- |
- |
0,51 |
0,47 |
0,001 |
1,4 |
3,0 |
1,66 |
4,2 |
|
1,00 |
- |
0,84 |
- |
- |
0,57 |
0,52 |
0,004 |
2,4 |
3,5 |
2,02 |
5,0 |
||
|
1,40 |
- |
1,03 |
0,88 |
0,75 |
0,68 |
0,62 |
0,004 |
2,7 |
- |
- |
- |
||
|
- |
1,65 |
1,14 |
- |
- |
0.74 |
0,67 |
0,005 |
2,9 |
-. |
- |
- |
||
|
- |
2,00 |
1,31 |
- |
- |
0,80 |
0,73 |
0,006 |
3,3 |
- |
- |
- |
||
|
- |
2,20 |
1,39 |
- |
- |
0,85 |
0,77 |
0.007 |
3.4 |
- |
- |
- |
||
|
1,25 |
1,00 |
|
0,77 |
- |
- |
0,55 |
0,50 |
0,003 |
2,2 |
5,0 |
1.96 |
4,5 |
|
|
1,50 |
- |
0,95 |
- |
- |
0,68 |
0,62 |
0,003 |
2,5 |
6,0 |
2,45 |
5,4 |
||
|
2,00 |
- |
1,13 |
- |
- |
0,79 |
0,72 |
0,003 |
2,7 |
_ |
- |
- |
||
|
2,50 |
- |
1,29 |
1,10 |
0,94 |
0,88 |
0,80 |
0,004 |
3,0 |
- |
- |
- |
||
|
- |
2,70 |
1,37 |
- |
- |
0,89 |
0,81 |
0,004 |
3,2 |
- |
- |
- |
||
|
- |
3,00 |
1,46 |
- |
- |
0,96 |
0,87 |
0,005 |
3,3 |
- |
- |
- |
||
|
- |
3,50 |
1,61 |
- |
- |
1,04 |
0,95 |
0,005 |
3,5 |
- |
- |
- |
||
|
- |
3,90 |
1,74 |
- |
- |
1,06 |
0,96 |
0,007 |
3,8 |
- |
- |
- |
||
|
1,50 |
2,50 |
|
1,19 |
- |
- |
0,81 |
0,74 |
0,003 |
2,9 |
7,0 |
2,24 |
4,4 |
|
|
2,80 |
- |
1,27 |
- |
- |
0,87 |
0,79 |
0,004 |
3,0 |
8,0 |
2,4 |
5,0 |
||
|
3,00 |
- |
1,32 |
- |
- |
0,90 |
0,82 |
0,004 |
3,0 |
8,5 |
2,58 |
5,3 |
||
|
3,50 |
- |
1,45 |
- |
- |
0,98 |
0,89 |
0,004 |
3,2 |
- |
- |
- |
||
|
3,90 |
- |
1,54 |
1,32 |
1,13 |
1,04 |
0,95 |
0,004 |
3,3 |
- |
- |
- |
||
|
- |
4,25 |
1,63 |
- |
- |
1,08 |
0,98 |
0,004 |
3,5 |
- |
- |
- |
||
|
- |
4,70 |
1,75 |
- |
- |
1,13 |
1,03 |
0,005 |
3,7 |
- |
- |
- |
||
|
- |
5,00 |
1,81 |
- |
- |
1,19 |
1,08 |
0,005 |
3,7 |
- |
- |
- |
||
|
- |
6,00 |
2,08 |
- |
- |
1,27 |
1,16 |
0,006 |
4,1 |
- |
- |
- |
||
|
2,00 |
4,50 |
- |
1,47 |
- |
- |
1,00 |
0,91 |
0,003 |
3,7 |
13,50 |
2,86 |
4,9 |
|
|
5,00 |
- |
1,55 |
- |
- |
1,08 |
0,99 |
0,003 |
3,3 |
14,50 |
3.01 |
5,1 |
||
|
5,50 |
- |
1,65 |
- |
- |
1,12 |
1,02 |
0,003 |
3,4 |
16,00 |
3.11 |
5,7 |
||
|
6,00 |
- |
1,73 |
- |
- |
1,18 |
1,08 |
0,003 |
3,5 |
16,5 |
3,22 |
5,8 |
||
|
6,50 |
- |
1,81 |
- |
- |
1,24 |
1,13 |
0,003 |
3,6 |
- |
- |
|
||
|
7,00 |
- |
1,90 |
- |
- |
1,28 |
1,17 |
0.033 |
3,7 |
- |
- |
- |
||
|
7,50 |
- |
1.98 |
- |
- |
1,33 |
1,21 |
0,003 |
3,8 |
- |
- |
- |
||
|
8,00 |
- |
2,06 |
1,76 |
1,50 |
1,37 |
1,25 |
0,004 |
3,9 |
- |
- |
- |
||
|
- |
8,50 |
2,14 |
- |
- |
1,42 |
1,29 |
0,004 |
4,0 |
- |
- |
- |
||
|
- |
9,00 |
2,22 |
- |
- |
1,45 |
1,33 |
0,004 |
4,1 |
- |
- |
- |
||
|
- |
9,50 |
2,31 |
- |
- |
1,49 |
1,36 |
0,004 |
4,2 |
- |
- |
- |
||
|
- |
10,00 |
2,38 |
- |
- |
1,54 |
1,40 |
0,004 |
4,3 |
- |
- |
- |
||
|
- |
10,50 |
2,46 |
- |
- |
1,59 |
1,45 |
0,004 |
4,3 |
- |
- |
- |
||
|
- |
11,00 |
2,54 |
- |
- |
1,60 |
1,46 |
0,005 |
4,5 |
- |
- |
- |
||
|
- |
12,50 |
! 2,78 |
- |
- |
1.70 |
1,55 |
0,005 |
4,8 |
- |
- |
- |
||
Примечания. 1. Глубина воды в концевом сечении конического звена.
2. В соответствии с. экспериментальными данными режим протекания воды в трубе с раструбным оголовком и коническим входным звеном приняты- безнапорный и напорный.
Переход от безнапорного
режима к напорному достигается при отношении ![]() , равном 1,16
, равном 1,16
3. Расчетный расход пропускается при безнапорном режиме протекания воды с обеспечением требуемого на протяжении всей трубы зазора (1/4 высоты трубы) между высшей точкой внутренней поверхности трубы и уровнем воды в трубе.
Максимальные расходы пропускаются частично при безнапорном режиме протекания воды, частично - при напорном.
Таблица 15.2
Трубы под автомобильные дороги
180 (инв. № 180/1)
|
Безнапорный режим |
Полунапорный режим |
Напорный режим |
|||||||||||
|
Тип оголовка |
Отверстие в м |
Q в м3/сек |
H в м |
H кр в м |
h сж в м |
i кр |
v вых в м/сек |
Q в м3/сек |
H в м |
v вых в м/сек |
Q в м3/сек |
H в м |
v вых в м/сек |
|
Портальный |
0,75 |
0,20 |
0,41 |
0,28 |
0,25 |
0,004 |
1,4 |
- |
- |
- |
- |
- |
- |
|
0,40 |
0,62 |
0,39 |
0,35 |
0,005 |
1,7 |
- |
- |
- |
- |
- |
- |
||
|
0,60 |
0,79 |
0,47 |
0,42 |
0,005 |
2,0 |
- |
- |
- |
- |
- |
- |
||
|
0,74 |
0,90 |
0,52 |
0.47 |
0,006 |
2,2 |
- |
- |
- |
- |
- |
- |
||
|
Раструбный с нормальным входным звеном |
1,00 |
0,60 |
0,68 |
0,44 |
0,40 |
0,004 |
2,1 |
1,60 |
1,30 |
3,3 |
- |
- |
- |
|
0,80 |
0.81 |
0,51 |
0,46 |
0,004 |
2,3 |
2,00 |
1,80 |
4,1 |
- |
- |
- |
||
|
1,00 |
0,93 |
0,58 |
0,52 |
0,004 |
2,4 |
2,40 |
2,34 |
4,9 |
- |
- |
- |
||
|
1,20 |
1,05 |
0,63 |
0,57 |
0,005 |
2,6 |
2,80 |
2,95 |
5,7 |
- |
- |
- |
||
|
1 40 |
1,46 |
0,68 |
0,61 |
0,005 |
2,8 |
3,00 |
3,16 |
6,0 |
- |
- |
- |
||
|
Раструбный оголовок с коническим входным звеном |
1,00 |
0,50 |
0,57 |
0,51 |
0,47 |
0,001 |
1,4 |
- |
- |
- |
3,00 |
1,66 |
4,2 |
|
1,00 |
0,84 |
0,57 |
0,52 |
0,004 |
2,4 |
- |
- |
- |
3,50 |
2,02 |
5,0 |
||
|
1,40 |
1,03 |
0,68 |
0,62 |
0,004 |
2,7 |
- |
- |
- |
- |
- |
- |
||
|
1,65 |
1,14 |
0,74 |
0,67 |
0,005 |
2,9 |
- |
- |
- |
- |
- |
- |
||
|
2,00 |
1 31 |
0,80 |
0,73 |
0,006 |
3,3 |
- |
- |
- |
- |
- |
- |
||
|
2,20 |
1,39 |
0,85 |
0,77 |
0,007 |
3,4 |
- |
- |
- |
- |
- |
- |
||
|
1,25 |
1,00 |
0,77 |
0,55 |
0,50 |
0,003 |
2,2 |
- |
- |
- |
5,00 |
1,96 |
4,5 |
|
|
1,50 |
0,95 |
0,68 |
0,62 |
0,003 |
2,5 |
- |
- |
- |
6,00 |
2,45 |
5,4 |
||
|
2,00 |
1,13 |
0,79 |
0,72 |
0,003 |
2,7 |
- |
- |
- |
- |
- |
- |
||
|
2,50 |
1,29 |
0,88 |
0,80 |
0,004 |
3,0 |
- |
- |
- |
- |
- |
- |
||
|
2,70 |
1,37 |
0,89 |
0,81 |
0,004 |
3,2 |
- |
- |
- |
- |
- |
- |
||
|
3,00 |
1,46 |
0,96 |
0,87 |
0,005 |
3,3 |
- |
- |
- |
- |
- |
- |
||
|
3,50 |
1,61 |
1,04 |
0,95 |
0,005 |
3,5 |
- |
- |
- |
- |
- |
- |
||
|
3,90 |
1,74 |
1.06 |
0,96 |
0,007 |
3,8 |
- |
- |
- |
- |
- |
- |
||
|
1,50 |
2,50 |
1,19 |
0,81 |
0,74 |
0,003 |
2,9 |
|
|
|
7,00 |
2,24 |
4,4 |
|
|
2,80 |
1,27 |
0,87 |
0,79 |
0,004 |
3,0 |
- |
- |
- |
8,00 |
2,40 |
5,0 |
||
|
3,00 |
1,32 |
0,90 |
0,82 |
0,004 |
3,0 |
- |
- |
- |
8,50 |
2,58 |
5,3 |
||
|
3,50 |
1,45 |
0,98 |
0,89 |
0,004 |
3,2 |
- |
- |
- |
- |
- |
- |
||
|
3,90 |
1,54 |
1,04 |
0,95 |
0,004 |
3,3 |
- |
- |
- |
- |
- |
- |
||
|
4,25 |
1,63 |
1,08 |
0,98 |
0,004 |
3,5 |
- |
- |
- |
- |
- |
- |
||
|
4,70 |
1,75 |
1,13 |
1,03 |
0,005 |
3,7 |
- |
- |
- |
- |
- |
- |
||
|
5,00 |
1,81 |
1,19 |
1,08 |
0,005 |
3,7 |
- |
- |
- |
- |
- |
- |
||
|
6,00 |
2,08 |
1,27 |
1,16 |
0,006 |
4,1 |
- |
- |
- |
- |
- |
- |
||
|
2,00 |
4,50 |
1,47 |
1,00 |
0,91 |
0,003 |
3,2 |
13,50 |
2,86 |
4,9 |
- |
- |
- |
|
|
5,00 |
1,55 |
1,08 |
0,99 |
0,003 |
3,3 |
14,50 |
3,01 |
5,1 |
- |
- |
- |
||
|
5,50 |
1,65 |
1,12 |
1,02 |
0,003 |
3.4 |
16,00 |
3,11 |
5,7 |
- |
- |
- |
||
|
6,00 |
1,73 |
1,18 |
1,08 |
0,003 |
3,5 |
16,50 |
3,22 |
5,1 |
- |
- |
- |
||
|
6,50 |
1,81 |
1,24 |
1,13 |
0,003 |
3,6 |
- |
- |
- |
- |
- |
- |
||
|
7,00 |
1,90 |
1,28 |
1,17 |
0,003 |
3,7 |
- |
- |
- |
- |
- |
- |
||
|
7,50 |
1,98 |
1,33 |
1,21 |
0,003 |
3,8 |
- |
- |
- |
- |
- |
- |
||
|
8,00 |
2,06 |
1,37 |
1,25 |
0,004 |
3,9 |
- |
- |
- |
- |
- |
- |
||
|
8,50 |
2,14 |
1,42 |
1,29 |
0,004 |
4,0 |
- |
- |
- |
- |
- |
- |
||
|
9,00 |
2,22 |
1,45 |
1,33 |
0,004 |
4,1 |
- |
- |
- |
- |
- |
- |
||
|
9,50 |
2,31 |
1,49 |
1,36 |
0,004 |
4,2 |
- |
- |
- |
- |
- |
- |
||
|
10,00 |
2,38 |
1,54 |
1,40 |
0,004 |
4,3 |
- |
- |
- |
- |
- |
- |
||
|
10,50 |
2 46 |
1,59 |
1,45 |
0,004 |
4,3 |
- |
- |
- |
- |
- |
- |
||
|
11,00 |
2,54 |
1,60 |
1,46 |
0,005 |
4,5 |
- |
- |
- |
- |
- |
- |
||
|
12,50 |
2,78 |
1,70 |
1,55 |
0,005 |
4,8 |
- |
- |
- |
- |
- |
- |
||
Примечание.
В соответствии с экспериментальными данными режимы протекания воды в трубе с
раструбным оголовком с нормальным входным звеном приняты - безнапорный и
полунапорный. Переход от безнапорного к напорному и полунапорному достигается
при отношении ![]() , равном 1,16
, равном 1,16
ПРИЛОЖЕНИЕ 16
ГИДРАВЛИЧЕСКИЕ ХАРАКТЕРИСТИКИ ТИПОВЫХ ПРЯМОУГОЛЬНЫХ ЖЕЛЕЗОБЕТОННЫХ ТРУБ
Таблица 16.1
Трубы под автомобильную дорогу
(Инв. № 180/1)
|
Безнапорный режим |
Полунапорный режим |
||||||||
|
Отверстие трубы в м |
Q в м3/сек |
Н в м |
h кр в м |
h сж в м |
i кр |
v вых в м/сек |
Q в м3/сек |
H в м |
v вых в м/сек |
|
2,00 х 2,00 |
1,00 |
0,45 |
0,30 |
0,27 |
0,004 |
1,8 |
15,40 |
2,88 |
6,1 |
|
2,00 |
0,71 |
0,48 |
0,43 |
0,004 |
2,3 |
16,00 |
2,99 |
6,3 |
|
|
3,00 |
0,94 |
0,63 |
0,56 |
0,004 |
2,7 |
16,50 |
3,07 |
6,5 |
|
|
4,00 |
1,13 |
0,77 |
0,69 |
0,005 |
2,9 |
17,00 |
3,16 |
6,7 |
|
|
5,00 |
1,32 |
0,89 |
0,79 |
0,005 |
3,2 |
17,50 |
3,25 |
6,9 |
|
|
6,00 |
1,48 |
1,00 |
0,90 |
0,006 |
3,4 |
18,00 |
3,35 |
7,1 |
|
|
7,00 |
1,66 |
1,11 |
0,99 |
0,006 |
3,5 |
19,00 |
3,56 |
7,5 |
|
|
8,00 |
1,82 |
1,22 |
1,03 |
0,006 |
3,9 |
20,00 |
3,75 |
7,9 |
|
|
9,00 |
1,97 |
1,31 |
1,11 |
0.007 |
4,1 |
21,00 |
3,97 |
8,3 |
|
|
10,00 |
2,11 |
1,41 |
1,19 |
0,007 |
4,2 |
- |
- |
- |
|
|
11,00 |
2,27 |
1,50 |
1,27 |
0,007 |
4,4 |
- |
- |
- |
|
|
12,60 |
2,49 |
1,64 |
1,36 |
0,008 |
4,6 |
- |
- |
- |
|
|
14,00 |
2,65 |
1,76 |
1,49 |
0,008 |
4.7 |
- |
- |
- |
|
|
15,00 |
2,77 |
1,85 |
1.56 |
0,008 |
4.8 |
- |
- |
- |
|
|
2,50 х 2,00 |
1,25 |
0,45 |
0,30 |
0,27 |
0,004 |
1,8 |
19,30 |
2,88 |
6,1 |
|
2,50 |
0,71 |
0,48 |
0,43 |
0,004 |
2,3 |
20,00 |
2,97 |
6,3 |
|
|
3,75 |
0,94 |
0,63 |
0,56 |
0,004 |
2,7 |
20,50 |
3,04 |
6,5 |
|
|
5,00 |
1,13 |
0,77 |
0,69 |
0,005 |
2,9 |
21,00 |
3,11 |
6,6 |
|
|
6,25 |
1,32 |
0,89 |
0,79 |
0,005 |
3,2 |
21,50 |
3,19 |
6,8 |
|
|
7,50 |
1,48 |
1,00 |
0,90 |
0,006 |
3,4 |
22,00 |
3,26 |
6,9 |
|
|
8,75 |
1,66 |
1,11 |
0,99 |
0,006 |
3,5 |
23,00 |
3,40 |
7,2 |
|
|
10,00 |
1,82 |
1,22 |
1,03 |
0,006 |
3,9 |
24,00 |
3,57 |
7,6 |
|
|
11,25 |
1,97 |
1,31 |
1,11 |
0,007 |
4,1 |
25,00 |
3,74 |
7,9 |
|
|
12,50 |
2,11 |
1,41 |
1,19 |
0,007 |
4,2 |
26,00 |
3,91 |
8,2 |
|
|
13,75 |
2,27 |
1,50 |
1,27 |
0,007 |
4,4 |
26,50 |
4,00 |
8,3 |
|
|
15,75 |
2,49 |
1,64 |
1,36 |
0,008 |
4,6 |
- |
- |
- |
|
|
17,50 |
2,65 |
1,76 |
1,49 |
0,008 |
4,7 |
- |
- |
- |
|
|
18,75 |
'2,77 |
1,85 |
1,56 |
0,008 |
4,8 |
- |
- |
- |
|
|
3,00 х 2,50 |
1,50 |
0,45 |
0,30 |
0,27 |
0,004 |
1,8 |
23,00 |
2,86 |
4,8 |
|
3,00 |
0,71 |
0,48 |
0,43 |
0,004 |
2,3 |
23,50 |
2,92 |
4,9 |
|
|
4,50 |
0,94 |
0,63 |
0,56 |
0,004 |
2.7 |
24,00 |
2,98 |
5,0 |
|
|
6,00 |
1,13 |
0,77 |
0,69 |
0,005 |
2,9 |
24,50 |
3,04 |
5,1 |
|
|
7,50 |
1,32 |
0,89 |
0,79 |
0,005 |
3,2 |
25,00 |
3,10 |
5,2 |
|
|
9,00 |
1,48 |
1,00 |
0,90 |
0,005 |
3,4 |
25,50 |
3,16 |
' 5,4 |
|
|
10,50 |
1,66 |
1,11 |
0,99 |
0,006 |
3,5 |
26,00 |
3,22 |
5,5 |
|
|
12,00 |
1,82 |
1,22 |
1,03 |
0,006 |
3,9 |
27,00 |
3,34 |
5,7 |
|
|
13,50 |
1,97 |
1,31 |
1,11 |
0,007 |
4,1 |
28,00 |
3,47 |
5,9 |
|
|
15,00 |
2,11 |
1,41 |
1,19 |
0,007 |
4,2 |
29,00 ' |
3,61 |
6,1 |
|
|
16,50 |
2,27 |
1,50 |
1,27 |
0,007 |
4,4 |
30.00 |
3,75 |
6,3 |
|
|
18,90 |
2 49 |
1,64 |
1,36 |
0,008 |
4,6 |
31,00 |
3,89 |
6,4 |
|
|
21,00 |
2,65 |
1,76 |
1,49 |
0,008 |
4,7 |
31,50 |
3,97 |
6,6 |
|
|
22,50 |
2,77 |
1,85 |
1 56 |
0,008 |
4,8 |
- |
- |
- |
|
|
4,00 х 2,50 |
2,00 |
0,45 |
0,30 |
0,27 |
0,004 |
1,8 |
31,00 |
2,99 |
4,9 |
|
4,00 |
0,71 |
0,48 |
0,43 |
0,004 |
2,3 |
32,00 |
2,98 |
5,0 |
|
|
6,00 |
0,94 |
0,63 |
0,56 |
0,004 |
2,7 |
33,00 |
3,07 |
5,2 |
|
|
8,00 |
1,13 |
0,77 |
0,69 |
0,005 |
2,9 |
34,00 |
3,16 |
5,4 |
|
|
10,00 |
1,32 |
0,89 |
0,79 |
0,005 |
3,2 |
35,00 |
3,25 |
5,5 |
|
|
12,00 |
1..48 |
1,00 |
0,90 |
0,006 |
3,4 |
36,00 |
3,35 |
5,7 |
|
|
14,00 |
1,66 |
1,11 |
0,99 |
0,006 |
3,5 |
37,00 |
3,44 |
5,8 |
|
|
16,00 |
1,82 |
1,22 |
1,03 |
0,006 |
3,9 |
38,00 |
3,54 |
6,0 |
|
|
18,00 |
1,97 |
1,31 |
I . U |
0,007 |
4,1 |
39,00 |
3,64 |
6,1 |
|
|
20,00 |
2,11 |
1,41 |
1,19 |
0,007 |
4,2 |
40,00 |
3,75 |
6,3 |
|
|
22,00 |
2,27 |
1,50 |
1,27 |
0,007 |
4,4 |
41,00 |
3,86 |
6,4 |
|
|
25,20 |
2,49 |
1,64 |
1,36 |
0,008 |
4,6 |
42,00 |
3,97 |
6,6 |
|
|
28,00 |
2,65 |
1,76 |
1,49 |
0,008 |
4,7 |
- |
- |
- |
|
|
30,00 |
2,77 |
1,85 |
1,56 |
0,008 |
4,8 |
- |
- |
- |
|
ПРЯМОУГОЛЬНЫЕ ЖЕЛЕЗОБЕТОННЫЕ ТРУБЫ
Таблица 16.2
Трубы под железную дорогу
(Инв. № 180/1)
|
Безнапорный режим |
Полунапорный режим |
||||||||||
|
Отверстие трубы в м |
Q расч в м3/сек |
Q макс в м3/сек |
H в м |
Нвх в м |
h кр в м |
h сж в м |
i кр |
v вых в м/сек |
Q в м3/сек |
H в м |
v вых в м/сек |
|
1,00 × 1,50 |
0,50 |
|
0,45 |
|
0,30 |
0,27 |
0,004 |
1,8 |
5,50 |
2,30 |
5,8 |
|
1,00 |
- |
0,71 |
- |
0,48 |
0,43 |
0,004 |
2,3 |
6,00 |
2,49 |
6,3 |
|
|
1,50 |
- |
0,94 |
- |
0,63 |
0,56 |
0,004 |
2,7 |
6,50 |
2,70 |
6,8 |
|
|
2,00 |
- |
1,13 |
- |
0,77 |
0,69 |
0,005 |
2,9 |
7,00 |
2,92 |
7,3 |
|
|
2,50 |
- |
1,32 |
- |
0,89 |
0,79 |
0,005 |
3,2 |
8,00 |
3,43 |
8,4 |
|
|
3,00 |
- |
1,48 |
- |
1,00 |
0,90 |
0,006 |
3,4 |
- |
- |
- |
|
|
3,50 |
- |
1,66 |
- |
1,11 |
0,99 |
0,006 |
3.5 |
- |
- |
- |
|
|
4,00 |
- |
1,82 |
- |
1,22 |
1,03 |
0,006 |
3,9 |
- |
- |
- |
|
|
4,60 |
- |
2,00 |
1,67 |
1,31 |
1,11 |
0,007 |
4,1 |
- |
- |
- |
|
|
- |
5,00 |
2,12 |
- |
1,41 |
1,19 |
0,007 |
4,2 |
- |
- |
- |
|
|
1,00 × 1,50 |
1,25 |
|
0,71 |
|
0,48 |
0,43 |
0,004 |
2,3 |
7,00 |
2,30 |
5,9 |
|
1,87 |
- |
0,94 |
- |
0,63 |
0,56 |
0,004 |
2,7 |
7,50 |
2,45 |
6,3 |
|
|
2,50 |
- |
1,13 |
- |
0,77 |
0,69 |
0,005 |
2,9 |
8,00 |
2,61 |
6,7 |
|
|
3,12 |
- |
1,32 |
- |
0,89 |
0,79 |
0,005 |
3,2 |
9,00 |
2,96 |
7,5 |
|
|
3,75 |
- |
1,48 |
- |
1,00 |
0,90 |
0,006 |
3,4 |
10,00 |
3,36 |
8,4 |
|
|
4,37 |
- |
1,66 |
- |
1,11 |
0,99 |
0,006 |
3,5 |
- |
- |
- |
|
|
5,00 |
- |
1,82 |
- |
1,22 |
1,03 |
0,006 |
3,9 |
- |
- |
- |
|
|
5,75 |
- |
2,00 |
1,67 |
1,31 |
1,11 |
0,007 |
4,1 |
- |
- |
- |
|
|
- |
6,25 |
2,12 |
- |
1,41 |
1,19 |
0,007 |
4,2 |
- |
- |
- |
|
|
1,50 × 2,00 |
0,75 |
- |
0,45 |
- |
0,30 |
0,27 |
0,004 |
1,8 |
11,60 |
2,89 |
6,1 |
|
1,50 |
- |
0,71 |
- |
0,48 |
0,43 |
0,004 |
2,3 |
12,00 |
2,99 |
6,3 |
|
|
2,25 |
- |
0,94 |
- |
0,63 |
0,56 |
0,004 |
2,7 |
12,50 |
3,10 |
6,5 |
|
|
3,00 |
- |
1,13 |
- |
0,77 |
0,69 |
0,005 |
2,9 |
13,00 |
3,23 |
6,8 |
|
|
3,75 |
- |
1,32 |
- |
0,89 |
0,79 |
0,005 |
3,2 |
14,00 |
3,48 |
7,3 |
|
|
4,50 |
- |
1,48 |
- |
1,00 |
0,90 |
0,006 |
3,4 |
15,00 |
3,75 |
7,9 |
|
|
5,25 |
- |
1,66 |
- |
1,11 |
0,99 |
0,006 |
3,5 |
15,80 |
3,99 |
8,3 |
|
|
6,00 |
- |
1,82 |
- |
1,22 |
1,03 |
0,006 |
3,9 |
- |
- |
- |
|
|
6,75 |
- |
1,97 |
- |
1,31 |
1,11 |
0,007 |
4,1 |
- |
- |
- |
|
|
7,50 |
- |
2,12 |
- |
1,41 |
1,19 |
0,007 |
4,2 |
- |
- |
- |
|
|
8,25 |
- |
2,27 |
- |
1,50 |
1,27 |
0,007 |
4,4 |
- |
- |
- |
|
|
9,45 |
- |
2,49 |
2,08 |
1,64 |
1,36 |
0,008 |
4,6 |
- |
- |
- |
|
|
- |
10,50 |
2,65 |
- |
1,76 |
1,49 |
0,008 |
4,7 |
- |
- |
- |
|
|
- |
11.25 |
2,77 |
|
1.85 |
1.56 |
0,008 |
4,8 |
- |
- |
- |
|
|
2,00 × 2,00 |
1,00 |
- |
0,45 |
|
0,30 |
0,27 |
0,004 |
1,8 |
15,40 |
2,88 |
6.1 |
|
2,00 |
- |
0,71 |
- |
0,48 |
0,43 |
0,004 |
2,3 |
16,00 |
2,99 |
6,3 |
|
|
3,00 |
- |
0,94 |
- |
0,63 |
0,56 |
0,004 |
2,7 |
16,50 |
3,07 |
6,5 |
|
|
4,00 |
- |
1,13 |
- |
0,77 |
0,69 |
0.005 |
2,9 |
17,00 |
3,16 |
6,7 |
|
|
5,00 |
- |
1,32 |
- |
0,89 |
0,79 |
0,005 |
3,2 |
17,50 |
3,25 |
6,9 |
|
|
6,00 |
- |
1,48 |
- |
1,00 |
0,90 |
0,006 |
3,4 |
18,00 |
3,35 |
7,1 |
|
|
7,00 |
- |
1,66 |
- |
1,11 |
0,99 |
0,006 |
3,5 |
19,00 |
3,56 |
7,5 |
|
|
8,00 |
- |
1,82 |
- |
1,22 |
1,03 |
0,006 |
3,9 |
20,00 |
3,75 |
7,9 |
|
|
9,00 |
- |
1,97 |
- |
1,31 |
1,11 |
0,007 |
4,1 |
21,00 |
3,97 |
8,3 |
|
|
10,00 |
- |
2,11 |
- |
1,41 |
1,19 |
0,007 |
4,2 |
- |
- |
- |
|
|
11,00 |
- |
2,27 |
- |
1,50 |
1,27 |
0,007 |
4,4 |
- |
- |
- |
|
|
12,60 |
- |
2,49 |
2,08 |
1,64 |
1,36 |
0,008 |
4,6 |
- |
- |
- |
|
|
- |
14,00 |
2,65 |
- |
1,76 |
1,49 |
0,008 |
4,7 |
- |
- |
- |
|
|
- |
15,00 |
2,77 |
- |
1,85 |
1,56 |
0,008 |
4,8 |
- |
- |
- |
|
|
2,50 × 2,00 |
1,25 |
|
0,45 |
|
0,30 |
0,27 |
0,004 |
1,8 |
19,30 |
2,88 |
6,1 |
|
2,50 |
- |
0,71 |
- |
0,48 |
0,43 |
0,004 |
2,3 |
20,00 |
2,97 |
6.3 |
|
|
3,75 |
- |
0,94 |
- |
0,63 |
0,56 |
0,004 |
2,7 |
20,50 |
3,04 |
6.5 |
|
|
5,00 |
- |
1,13 |
- |
0,77 |
0,69 |
0,005 |
2,9 |
21,00 |
3,11 |
6,6 |
|
|
6,25 |
- |
1,32 |
- |
0,89 |
0,79 |
0,005 |
3,2 |
21,50 |
3,19 |
6.8 |
|
|
7,50 |
- |
1,48 |
- |
1,00 |
0,90 |
0,006 |
3,4 |
22,00 |
3,26 |
6,9 |
|
|
8,75 |
- |
1,66 |
- |
1,11 |
0,99 |
0,006 |
3,5 |
23,00 |
3,40 |
7,2 |
|
|
10,00 |
- |
1,82 |
- |
1,22 |
1,03 |
0,006 |
3,9 |
24,00 |
3,57 |
7,6 |
|
|
11,25 |
- |
1,97 |
- |
1,31 |
1,11 |
0,007 |
4,1 |
25,00 |
3,74 |
7,9 |
|
|
12.50 |
- |
2,11 |
- |
1,41 |
1,19 |
0,007 |
4,2 |
26,00 |
3,91 |
8,2 |
|
|
13,75 |
- |
2,27 |
- |
1,50 |
1,27 |
0,007 |
4,4 |
26,50 |
4,00 |
8,3 |
|
|
15,75 |
- |
2,49 |
2,08 |
1,64 |
1,36 |
0,008 |
4,6 |
- |
- |
- |
|
|
- |
17,50 |
2,65 |
- |
1,76 |
1,49 |
0,008 |
4,7 |
- |
- |
- |
|
|
- |
18,75 |
2,77 |
- |
1,85 |
1,56 |
0,008 |
4,8 |
- |
- |
- |
|
|
3,00 × 2,50 |
1,50 |
|
0,45 |
|
0,30 |
0,27 |
0,004 |
1,8 |
23,00 |
2,86 |
4,8 |
|
3,00 |
- |
0,71 |
- |
0,48 |
0,43 |
0,004 |
2,3 |
23,50 |
2,92 |
4,9 |
|
|
4,50 |
- |
0,94 |
- |
0,63 |
0,56 |
0,004 |
2,7 |
24,00 |
2,98 |
5.0 |
|
|
6,00 |
- |
1,13 |
- |
0,77 |
0,69 |
0,005 |
2,9 |
24,50 |
3,04 |
5,1 |
|
|
7,50 |
- |
1,32 |
- |
0,89 |
0,79' |
0,005 |
3,2 |
25,00 |
3,10 |
5,2 |
|
|
9,00 |
- |
1,48 |
- |
1,00 |
0,90 |
0,006 |
3,4 |
25,50 |
3,16 |
5.4 |
|
|
10,50 |
- |
1,66 |
- |
1,11 |
0,99 |
0,006 |
3,5 |
26,00 |
3,22 |
5,5 |
|
|
12,00 |
- |
1,82 |
- |
1,22 |
1,03 |
0,006 |
3,9 |
27,00 |
3,34 |
5,7 |
|
|
13,50 |
- |
1,97 |
- |
1,31 |
1,11 |
0,007 |
4,1 |
28,00 |
3,47 |
5,9 |
|
|
15,00 |
- |
2,11 |
- |
1,41 |
1.19 |
0,007 |
4,2 |
29,00 |
3,61 |
6,1 |
|
|
16,50 |
- |
2,27 |
- |
1,50 |
1,27 |
0,007 |
4,4 |
30,00 |
3,75 |
6,3 |
|
|
18,90 |
- |
2,49 |
2,08 |
1,64 |
1,36 |
0,008 |
4,6 |
31,00 |
3,89 |
6,4 |
|
|
- |
21,0 |
2,65 |
- |
1,76 |
1,49 |
0,008 |
4.7 |
31,50 |
3,97 |
6,6 |
|
|
- |
22,50 |
2,77 |
- |
1,85 |
1,56 |
0,008 |
4,8 |
- |
- |
- |
|
|
4,00 × 2,50 |
2,0 |
- |
0,45 |
- |
0,30 |
0,27 |
0,004 |
1,8 |
31,00 |
2,89 |
4,9 |
|
4,0 |
- |
0,71 |
- |
0,48 |
0,43 |
0,004 |
2,3 |
32,00 |
2,98 |
5,0 |
|
|
6,0 |
- |
0,94 |
- |
0,63 |
0,56 |
0,004 |
2,7 |
33,00 |
3,07 |
5,2 |
|
|
8,0 |
- |
1,13 |
- |
0,77 |
0,69 |
0,005 |
2,9 |
34,00 |
3,16 |
5,4 |
|
|
10,0 |
|
1,32 |
- |
0,89 |
0,79 |
0,005 |
3,2 |
35,00 |
3,25 |
5,5 |
|
|
12,0 |
- |
1,48 |
- |
1,00 |
0,90 |
0,006 |
3,4 |
36,00 |
3,35 |
5,7 |
|
|
14,0 |
- |
1,66 |
- |
1,11 |
0,99 |
0,006 |
3,5 |
37,00 |
3,44 |
5,8 |
|
|
16,0 |
- |
1,82 |
- |
1,22 |
1,03 |
0,006 |
3,9 |
38,00 |
3,54 |
6,0 |
|
|
18,0 |
- |
1,97 |
- |
1,31 |
1,11 |
0,007 |
4,1 |
39,00 |
3,64 |
6,1 |
|
|
20,0 |
- |
2,11 |
- |
1,41 |
1,19 |
0,007 |
4,2 |
40,00 |
3,75 |
6,3 |
|
|
22,0 |
- |
2,27 |
- |
1,50 |
1,27 |
0,007 |
4,4 |
41,00 |
3,86 |
6,4 |
|
|
25,20 |
- |
2,49 |
2,08 |
1,64 |
1,36 |
0,008 |
4,6 |
42,00 |
3,97 |
6,6 |
|
|
- |
28,0 |
2,65 |
- |
1,76 |
1,49 |
0,008 |
4,7 |
- |
- |
- |
|
|
- |
30,0 |
2,77 |
- |
1,85 |
1,56 |
0,008 |
4,8 |
- |
- |
- |
|
Таблица 16.3
ПРЯМОУГОЛЬНЫЕ ЖЕЛЕЗОБЕТОННЫЕ И БЕТОННЫЕ ТРУБЫ
Трубы с нормальным входным звеном (инв. № 7661)*
Высота трубы в свету h0 = 3,1 м
|
Отверстие в свету b 0 в м |
Расчетный расход Q расч в м3/сек |
Критическая глубина h кр в м |
Подпор H в м |
Критическая скорость v кр в м/сек |
Скорость на выходе v вых в м/сек |
Критический уклон i кр |
Наименьшее расстояние от обреза фундамента до подошвы рельса по конструктивным условиям H мин в м |
Примечание |
|
2,0 |
18,0 |
2,02 |
3,55 |
4,46 |
4,95 |
0,006 |
4,46 4,80 |
В числителе H мин для железобетонных труб, знаменателе для бетонных |
|
2,5 |
22,5 |
2,02 |
3,55 |
4,46 |
4,95 |
0,005 |
4,54 |
Только железобетонные |
|
3,0 |
27,0 |
2,02 |
3,55 |
4,46 |
4,95 |
0,004 |
4,60 4,92 |
В числителе H мин для железобетонных труб, в знаменателе - для бетонных |
|
4.0 |
36,0 |
2,02 |
3,55 |
4,46 |
4,95 |
0,003 |
5,03 |
Только бетонные |
|
5,0 |
45,0 |
2,02 |
3,55 |
4,46 |
4,95 |
0,003 |
5,13 |
То же |
|
6,0 |
54,0 |
2 02 |
3,55 |
4,46 |
4,95 |
0,003 |
5,17 |
» |
* Таблицы 16.3-16.6 приводятся в качестве справочных данных для эксплуатируемых сооружений, ввиду того, что срок действия указанных проектов был продлен только до 1/1 1967 г.
ПРЯМОУГОЛЬНЫЕ ЖЕЛЕЗОБЕТОННЫЕ И БЕТОННЫЕ ТРУБЫ
(инв. № 7661)
Таблица 16.4
Трубы с повышенным входным звеном (высота в свету повышенного звена hпв =3,9 м,
высота в свету трубы h0 = 3,1 м)
|
Отверстие в свету b 0 в м |
Расчетный расход Q расч в м3/сек |
Критическая глубина h кр в м |
Подпор H в м |
Критическая скорость v кр в м/сек |
Скорость на выходе v вых в м/сек |
Критический уклон i кр |
Наименьшее расстояние от обреза фундамента до подошвы рельса по конструктивным условиям H мин в м |
Примечание |
|
2,0 |
26,0 |
2,58 |
4,65 |
5,04 |
5,62 |
0,006 |
4,46 4,80 |
В числителе H мин для железобетонных труб, знаменателе для бетонных |
|
2,5 |
32,5 |
2,58 |
4,65 |
5,04 |
5,62 |
0,005 |
4,54 |
Только железобетонные |
|
3,0 |
39,0 |
2,58 |
4,65 |
5,04 |
5,62 |
0,005 |
4,60 4,92 |
В числителе H мин для железобетонных труб, в знаменателе - для бетонных |
|
4,0 |
52,0 |
2,58 |
4,65 |
5,04 |
5,62 |
0,004 |
5,03 |
Только бетонные |
|
5,0 |
65,0 |
2,58 |
4,65 |
5,04 |
5,62 |
0,003 |
5,13 |
То же |
|
6,0 |
78,0 |
2,58 |
4,65 |
5,04 |
5,62 |
0,003 |
5,17 |
» |
ПРЯМОУГОЛЬНЫЕ БЕТОННЫЕ ТРУБЫ (инв. № 8822)
Таблица 16.5
Трубы с нормальным входным звеном
|
Тип оголовков |
Отверстие в свету b 0 в м |
Высота в свету h 0 в м |
Расчетный расход Q расч в м3/сек |
Критическая глубина h кр в м |
Подпор H в м |
Критическая скорость v кр в м/сек |
Скорость на выходе v вых в м/сек |
Критический уклон i кр |
Наименьшее расстояние от обреза фундамента до подошвы рельса по конструктивным условиям H мин в м |
|
Портальный |
1,5 2,0 |
1,5 1,5 |
4,5 6,0 |
0,98 0,98 |
1,8 1,8 |
3,06 3,06 |
3,4 3,4 |
0,005 0,004 |
3,05 3,60 |
|
Со срезанными откосными стенками |
1,5 2,0 |
2,0 2,0 |
7,5 10,0 |
1,37 1,37 |
2,42 2,42 |
3,66 3,66 |
4,1 4,1 |
0,006 0,005 |
3,05 3,60 |
Таблица 16.6
ТРУБЫ С ПОВЫШЕННЫМ ВХОДНЫМ ЗВЕНОМ (инв. № 8822)
|
Тип оголовков |
Отверстие в свету b 0 в м |
Высота в свету h 0 в м |
Высота повышенного звена h пов в м |
Расчетный расход Q расч в м3/сек |
Критическая глубина h кр в м |
Подпор H в м |
Критическая скорость v кр в м/сек |
Скорость на выходе v вых в м/сек |
Критический уклон i кр |
Наименьшее расстояние от обреза фундамента до подошвы рельса по конструктивным условиям H мин в м |
|
Со срезанными откосными стенками |
1,5 |
1,5 |
2,0 |
6,6 |
1,25 |
2,20 |
3,52 |
3,9 |
0,005 |
3,05 |
|
2,0 |
1,5 |
2.0 |
8,8 |
1,25 |
2,20 |
3,52 |
3,9 |
0,004 |
3,60 |
|
|
1,5 |
2,0 |
2,5 |
10,2 |
1,67 |
2,92 |
4,08 |
4,5 |
0,006 |
3,05 |
|
|
2,0 |
2,0 |
2,5 |
13,6 |
1,67 |
2,92 |
4,08 |
4,5 |
0,005 |
3,60 |
ПРИЛОЖЕНИЕ 17
ЗНАЧЕНИЕ КОЭФФИЦИЕНТА m0 ДЛЯ ВОДОСЛИВА С ТОНКОЙ СТЕНКОЙ
|
Подпор в м |
Высота стенки водослива со стороны верхнего бьефа в м |
|||||||||
|
0,2 |
0,3 |
0,4 |
0,5 |
0,6 |
0,8 |
1,0 |
1,5 |
2,0 |
3,0 |
|
|
0,14 |
0,464 |
0,448 |
0,440 |
0,436 |
0,433 |
0,430 |
0,428 |
0,426 |
0,425 |
0,424 |
|
0,16 |
0,468 |
0,450 |
0,441 |
0,436 |
0,432 |
0,428 |
0,426 |
0,424 |
0,423 |
0,422 |
|
0,18 |
0,472 |
0,453 |
0,442 |
0,436 |
0,432 |
0,428 |
0,425 |
0,423 |
0,422 |
0,420 |
|
0,20 |
0,476 |
0,455 |
0,444 |
0,437 |
0,433 |
0,428 |
0,425 |
0,422 |
0,420 |
0,419 |
|
0,22 |
0,480 |
0,460 |
0,446 |
0,439 |
0,434 |
0,428 |
0,425 |
0,421 |
0,420 |
0,417 |
|
0,24 |
0,484 |
0,462 |
0,440 |
0,448 |
0,435 |
0,428 |
0,425 |
0,421 |
0,419 |
0,416 |
|
0,26 |
0,488 |
0,467 |
0,451 |
0,442 |
0,436 |
0,429 |
0,425 |
0,420 |
0,418 |
0,415 |
|
0,28 |
0,492 |
0,468 |
0,453 |
0,444 |
0,438 |
0,430 |
0,426 |
0,420 |
0,418 |
0,415 |
|
0,30 |
0,496 |
0,471 |
0,456 |
0,446 |
0,439 |
0,431 |
0,426 |
0,420 |
0,418 |
0,414 |
|
0,35 |
- |
0,479 |
0,462 |
0,451 |
0,444 |
0,434 |
0,428 |
0,421 |
0,418 |
0,413 |
|
0,40 |
- |
0,486 |
0,468 |
0,457 |
0,448 |
0,437 |
0,430 |
0,422 |
0,417 |
0,412 |
|
0,45 |
- |
0,492 |
0,474 |
0,462 |
0,452 |
0,440 |
0,434 |
0,423 |
0,419 |
0,411 |
|
0,50 |
- |
0,499 |
0,480 |
0,467 |
0,457 |
0,444 |
0,436 |
0,425 |
0,419 |
0,410 |
|
0,60 |
- |
- |
0,491 |
0,477 |
0,466 |
0,451 |
0,441 |
0,428 |
0,421 |
0,410 |
|
0,70 |
- |
- |
0,500 |
0,485 |
0,474 |
0,458 |
0,447 |
0,432 |
0,424 |
0,409 |
ПРИЛОЖЕНИЕ 18
ГРАФИКИ ПРОПУСКНОЙ СПОСОБНОСТИ ТРУБ ДЛЯ РАСЧЕТА ОТВЕРСТИЙ С УЧЕТОМ АККУМУЛЯЦИИ
Круглые одноочковые трубы диаметром 1,0-2,0 м с коническими входными и выходными звеньями под железную и автомобильную дороги
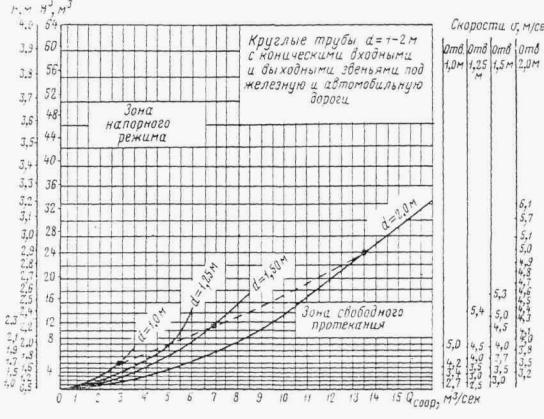
ПРИЛОЖЕНИЕ 19
Круглые ДВУХочковые трубы диаметром 1,0-2,0 м с коническими входными и выходными звеньями под железную и автомобильную дороги
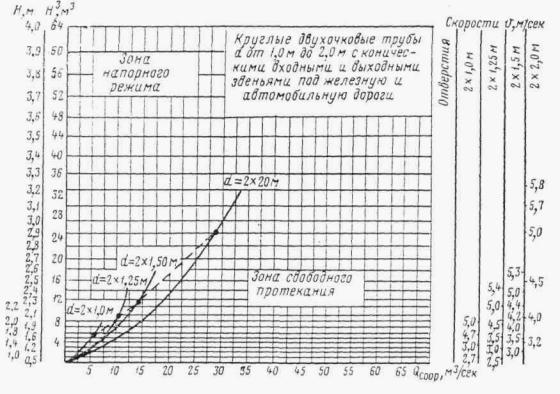
ПРИЛОЖЕНИЕ 20
Круглые ТРЕХочковые трубы диаметром 1,0-2,0 м с коническими входными и выходными звеньями под железную и автомобильную дороги
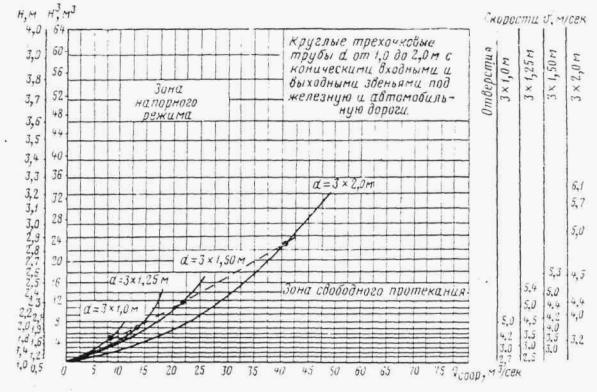
ПРИЛОЖЕНИЕ 21
Прямоугольные трубы с повышенными входными звеньями отверстиями 1,0 м, 1,25 м и 1,5 м под железную дорогу
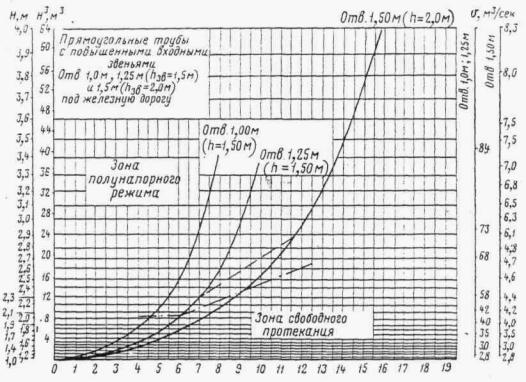
ПРИЛОЖЕНИЕ 22
Прямоугольные трубы отверстиями 2,0 м, 2,5, 3 и 4 м под железную и автомобильную дороги
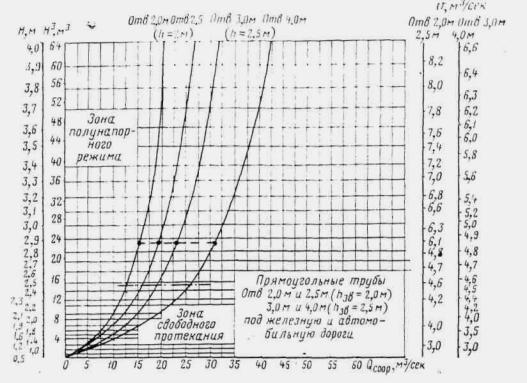
ПРИЛОЖЕНИЕ 23
Прямоугольные двухочковые трубы отверстиями 2 ×2 , и 2 ×2,5 м, 2 ×3 и 2 ×4 м под железную и автомобильную дороги
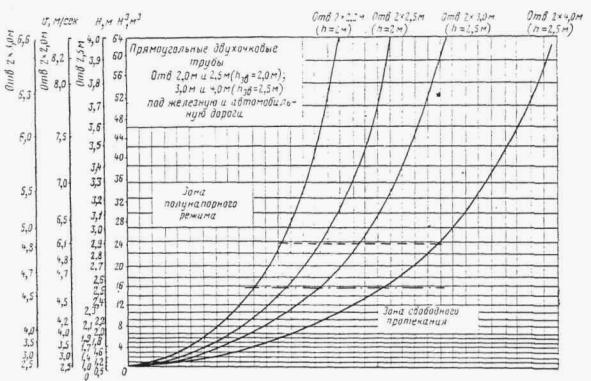
ПРИЛОЖЕНИЕ 24
Прямоугольные двухочковые трубы с повышенными входными звеньями отверстиями 1,25 м и 1,5 м под железную дорогу
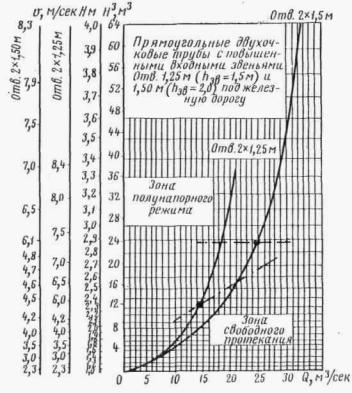
ПРИЛОЖЕНИЕ 25
График для определения площади живого сечения в круглой трубе
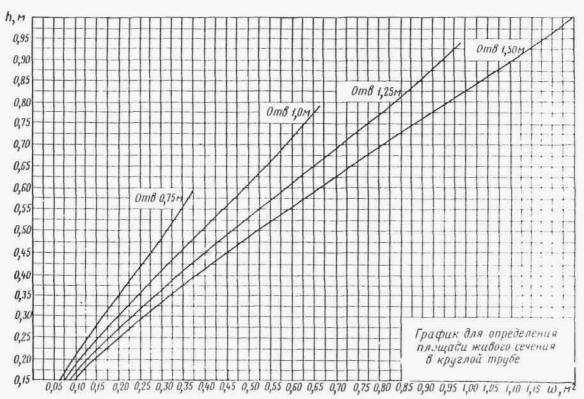
График
составлен по формуле ![]() (
( ![]() - sin
a)
- sin
a)
ПРИЛОЖЕНИЕ 26
График для определения гидравлического радиуса в круглой трубе
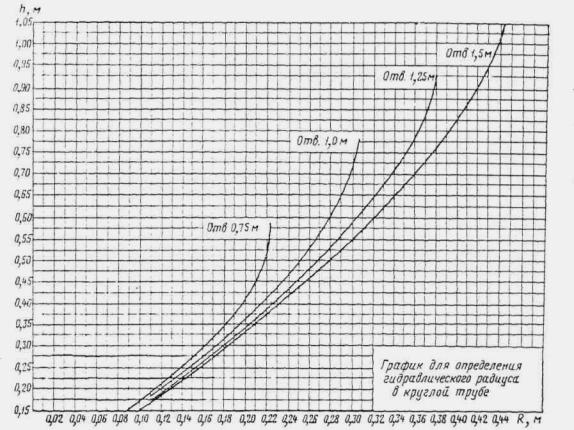
График
составлен по формуле ![]()
ПРИЛОЖЕНИЕ 27
График для определения смоченного периметра в круглой трубе
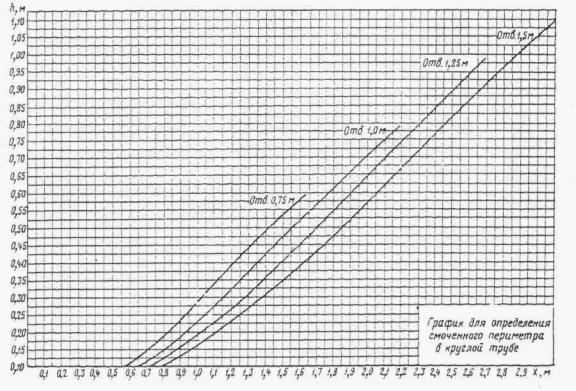
График
составлен по формуле ![]()
ПРИЛОЖЕНИЕ 28
ГРАФИК ДЛЯ ОПРЕДЕЛЕНИЯ КРИТИЧЕСКОЙ ГЛУБИНЫ В КРУГЛОЙ ТРУБЕ
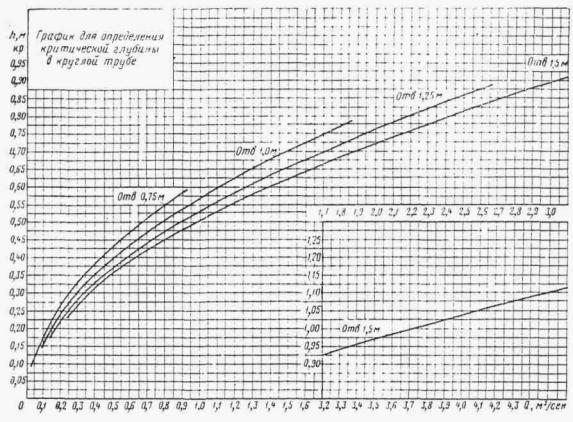
График
составлен по формуле ![]()
ПРИЛОЖЕНИЕ 29
ТИПЫ КОНСТРУКЦИЙ ПОВЫШЕННОЙ ШЕРОХОВАТОСТИ
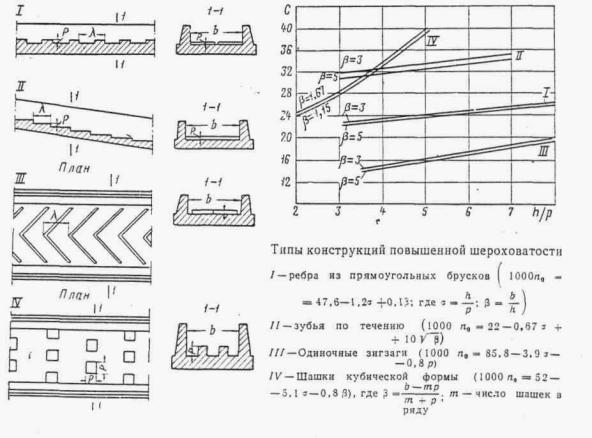
ПРИЛОЖЕНИЕ 30
ГРАФИК ДЛЯ ОПРЕДЕЛЕНИЯ СЖАТОЙ ГЛУБИНЫ И СОПРЯЖЕННОЙ С НЕЙ
В РУСЛАХ ПРЯМОУГОЛЬНОГО СЕЧЕНИЯ
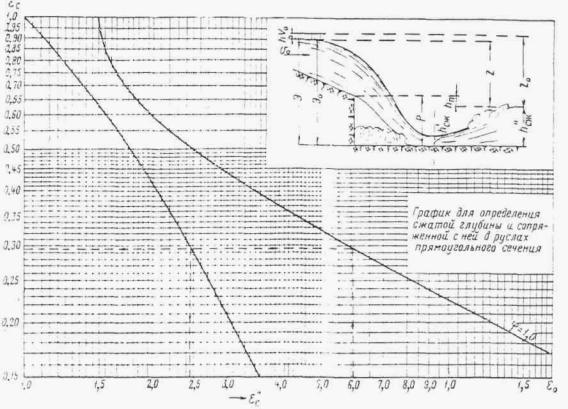
Пример.
Дано: р = 1,0 м Q = 4,0 м3/сек b = 2,0 м; vп = 8,0 м/сек h = 0,125 м.
Вычисляем
Э0
= 1,0 + 0,125 + =4,385: q =![]()
![]()
= 2,0 м2/сек.
По графику приложения 9.2 определяется hкр
= 0,74 м; ![]() ;
; ![]() м
м
![]()
По графику находим:
εс
= 0,296; hсж = 0,74·0,296 = 0,219
м; ε˝с = 2,44; h˝сж = 0,74·2,44 =
1,81 м; ![]()
где hсж - глубина воды в сжатом сечении; hкр -критическая глубина;
![]()
hсж - сопряженная глубина;
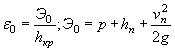
p - высота перепада; hп и v n -глубина воды и скорость на пороге.
ПРИЛОЖЕНИЕ 31
ГИДРАВЛИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПРЯМОУГОЛЬНЫХ, ТАВРОВЫХ И ДВУХСТРУйНЫХ ОЛОДЦЕВ НА ВХОДЕ (СО СТЕНКОЙ ПАДЕНИЯ)
|
Удельный расход q в м3/сек |
Высота стенки падения р в м |
Скорость подходов воды v в м/сек |
Глубина в сжатом сечении h сж в м |
Взаимная глубина h 2 в м |
Дальность падения струи l 1 в м |
Длина колодца в м |
Глубина воды в колодце H =1,05 h 2 в м |
Скорость в сжатом сечении v сжр в м/сек |
||
|
Прямоугольного l пр |
Таврового l тавр |
Двухструйного L дв |
||||||||
|
0,5 |
2,0 |
8 |
0,05 |
0,98 |
5,16 |
8,30 |
7,12 |
5.21 |
1,03 |
10,0 |
|
7 |
0,06 |
0,94 |
4,52 |
7,52 |
6,40 |
4.58 |
0,98 |
9,2 |
||
|
6 |
0,06 |
0,90 |
3,87 |
6.75 |
5,67 |
3 93 |
0,94 |
8,3 |
||
|
5 |
0,07 |
0,87 |
3,24 |
6,02 |
4,98 |
3,31 |
0,91 |
7,7 |
||
|
4 |
0,07 |
0,84 |
2,60 |
5,29 |
4,28 |
2,67 |
0,88 |
7,2 |
||
|
3 |
0,08 |
0,82 |
1,96 |
4,57 |
3,60 |
2,04 |
0,86 |
6,7 |
||
|
2 |
0,08 |
0,79 |
1,32 |
3,85 |
2,90 |
1,40 |
0,83 |
6,3 |
||
|
2,5 |
8 |
0,05 |
0,99 |
5,73 |
8,90 |
7,71 |
5,78 |
1,04 |
10,0 |
|
|
7 |
0,06 |
0,96 |
5,01 |
8.06 |
6,93 |
5,07 |
1,00 |
9.2 |
||
|
6 |
0,06 |
0.92 |
4,28 |
7,23 |
6,12 |
4.34 |
0.96 |
Ы |
||
|
5 |
0,07 |
0,89 |
3,58 |
6,43 |
5,36 |
3,63 |
0.93 |
7,7 |
||
|
4 |
0,07 |
0,86 |
2,88 |
5,64 |
4,60 |
2.95 |
0,90 |
7,12 |
||
|
3 |
0,07 |
0,84 |
2,17 |
4,86 |
3,85 |
2,24 |
0,88 |
6,9 |
||
|
2 |
0,08 |
0,82 |
1,46 |
4,08 |
3,10 |
1,54 |
0,86 |
6,7 |
||
|
3,0 |
8 |
0,05 |
1,00 |
6,30 |
9,50 |
8,30 |
6,35 |
1,05 |
10,0 |
|
|
7 |
0,06 |
0,97 |
5,50 |
8,60 |
7,44 |
5,56 |
1,02 |
9,2 |
||
|
6 |
0 06 |
0,94 |
4,70 |
7,71 |
6,58 |
4.76 |
0,99 |
8,3 |
||
|
5 |
0,07 |
0,91 |
3,93 |
6,84 |
5,75 |
4.00 |
0,96 |
7,7 |
||
|
4 |
0,07 |
0,88 |
3,16 |
5,98 |
4,92 |
3,23 |
0,92 |
7,2 |
||
|
3 |
0,07 |
0 87 |
2,38 |
5,15 |
4,12 |
2,45 |
0,90 |
7,2 |
||
|
2 |
0,07 |
0,85 |
1,60 |
4,32 |
3,30 |
1,67 |
0,89 |
7,2 |
||
|
3,5 |
8 |
0,05 |
1,02 |
6,78 |
10,06 |
8,82 |
6,83 |
1,08 |
10,0 |
|
|
7 |
0,05 |
1,00 |
5.92 |
9,11 |
7,92 |
5,97 |
1,04 |
9,6 |
||
|
6 |
0,06 |
0,97 |
5,06 |
8,16 |
7,00 |
5,12 |
1,02 |
9,2 |
||
|
5 |
0,06 |
0,94 |
4,23 |
7,24 |
6,11 |
4,29 |
0,98 |
8,5 |
||
|
4 |
0,07 |
0,91 |
3,40 |
6,32 |
5,22 |
3,47 |
0,96 |
7,7 |
||
|
3 |
0,07 |
0,90 |
2,56 |
5,43 |
4,36 |
2,63 |
0,94 |
7,7 |
||
|
2 |
0,07 |
0,88 |
1,72 |
4,54 |
3,48 |
1,79 |
0,92 |
7,7 |
||
|
4,0 |
8 |
0,05 |
1,05 |
7,25 |
10,61 |
9,35 |
7,30 |
1,10 |
10,0 |
|
|
7 |
0,05 |
1,02 |
6,34 |
9,62 |
8,38 |
6,39 |
1,07 |
10,0 |
||
|
6 |
0,05 |
0,99 |
5,42 |
8,62 |
7,40 |
5,47 |
1,04 |
10,0 |
||
|
5 |
0,06 |
0,97 |
4,54 |
7,64 |
6,48 |
4,60 |
1,02 |
9,2 |
||
|
4 |
0.06 |
0,94 |
3.65 |
6,66 |
5,53 |
3,71 |
0,99 |
8,3 |
||
|
3 |
0,06 |
0,92 |
2,74 |
5,70 |
4,58 |
2,80 |
0,98 |
8,3 |
||
|
2 |
0,06 |
0,91 |
1,84 |
4,73 |
3,66 |
1,90 |
0,96 |
8,3 |
||
|
4,5 |
8 |
0,05 |
1,05 |
7,70 |
11,06 |
9,80 |
7,75 |
1,10 |
10,1 |
|
|
7 |
0,05 |
1,02 |
6,73 |
10,01 |
8,77 |
6,78 |
1,07 |
10,0 |
||
|
6 |
0,05 |
1,00 |
5,76 |
8,96 |
7,76 |
5,81 |
1,04 |
10,0 |
||
|
5 |
0,06 |
0,97 |
4,82 |
7,94 |
6,76 |
4,88 |
1,02 |
9,2 |
||
|
4 |
0,06 |
0,95 |
3,88 |
6,92 |
5,78 |
3,94 |
1,00 |
8,3 |
||
|
3 |
0,06 |
0,94 |
2,91 |
5,91 |
4,79 |
2,97 |
0,99 |
8,3 |
||
|
2 |
0,06 |
0,92 |
1,94 |
4,90 |
3,78 |
2,00 |
0,98 |
8,3 |
||
|
5,0 |
8 |
0,05 |
1,05 |
8,15 |
11,51 |
10,25 |
8,20 |
1,10 |
10,0 |
|
|
7 |
0,05 |
1,02 |
7,12 |
10,40 |
9,16 |
7,17 |
1,08 |
10,0 |
||
|
6 |
0,05 |
1,00 |
6,10 |
9,30 |
8,10 |
6,15 |
1,05 |
10,0 |
||
|
5 |
0,06 |
0,98 |
5,10 |
8,24 |
7,06 |
5,16 |
1,03 |
9,2 |
||
|
4 |
0,06 |
0,96 |
4,10 |
7,17 |
6,02 |
4,16 |
1,01 |
8,3 |
||
|
3 |
0,06 |
0,95 |
3,08 |
6,12 |
4,98 |
3,14 |
1,00 |
8,3 |
||
|
о |
0.06 |
0,94 |
2,05 |
5,06 |
3,93 |
2,11 |
0.99 |
8,3 |
||
|
1,0 |
2,0 |
8 |
0,11 |
1,38 |
5,20 |
9,62 |
7,96 |
5,31 |
1,45 |
9,1 |
|
7 |
0,12 |
1,32 |
4,55 |
8,79 |
7,19 |
4,67 |
1,39 |
8,4 |
||
|
6 |
0,13 |
1,27 |
3,90 |
7,96 |
6,44 |
4,03 |
1,33 |
7,7 |
||
|
5 |
0,14 |
1,22 |
3,27 |
7,16 |
5,71 |
3,41 |
1,28 |
7,2 |
||
|
4 |
0,15 |
1,16 |
2,64 |
6,35 |
4,96 |
2,79 |
1,22 |
6,7 |
||
|
3 |
0,16 |
1,14 |
2,00 |
5,64 |
4,28 |
2,16 |
1,20 |
6,5 |
||
|
9 |
0,16 |
1,12 |
1,36 |
1,94 |
3,60 |
1,52 |
1,18 |
6,3 |
||
|
2,5 |
8 |
0,10 |
1,39 |
5,76 |
10,21 |
8,54 |
5,86 |
1,46 |
9,6 |
|
|
7 |
0,12 |
1,34 |
5,04 |
9,34 |
7,72 |
5,16 |
1,40 |
8,8 |
||
|
6 |
0,12 |
1,29 |
4,33 |
8,46 |
6,91 |
4,45 |
4,36 |
8,0 |
||
|
5 |
0,13 |
1,24 |
3,62 |
7,60 |
6,10 |
3,75 |
1,31 |
7,6 |
||
|
4 |
0.14 |
1,20 |
2,92 |
6,74 |
5,32 |
3,06 |
1,26 |
7,2 |
||
|
3 |
0,15 |
1,18 |
2,21 |
5,97 |
4,57 |
2,36 |
1,24 |
6,9 |
||
|
2 |
0,15 |
1,16 |
1,50 |
5,20 |
3,82 |
1,65 |
1,22 |
6,7 |
||
|
3,0 |
8 |
0,10 |
1,40 |
6,32 |
10,80 |
9,12 |
6,42 |
1.47 |
10,0 |
|
|
7 |
0,11 |
1,36 |
5,54 |
9,88 |
8,25 |
5,65 |
1,42 |
9,2 |
||
|
6 |
0,12 |
1,31 |
4,76 |
8,95 |
7,38 |
4,88 |
1,38 |
8,3 |
||
|
5 |
0,12 |
1,27 |
3,98 |
8,04 |
6,52 |
4,10 |
1,34 |
8,0 |
||
|
4 |
0,13 |
1,23 |
3,20 |
7,14 |
5,66 |
3,33 |
1,29 |
7,7 |
||
|
3 |
0,14 |
1,22 |
2,42 |
6,30 |
4,86 |
2,56 |
1,28 |
7,4 |
||
|
2 |
0,14 |
1,20 |
1,63 |
5,47 |
4,03 |
1,77 |
1,26 |
7,2 |
||
|
3,5 |
8 |
0,10 |
1,44 |
6,81 |
11,40 |
9,69 |
6,91 |
1,50 |
10,0 |
|
|
7 |
0,10 |
1,39 |
5,96 |
10,40 |
8,74 |
6,06 |
1,46 |
9,4 |
||
|
6 |
0,12 |
1,34 |
5,12 |
9,40 |
7,80 |
5,24 |
1,41 |
8,7 |
||
|
5 |
0,12 |
1,30 |
4,28 |
8,46 |
6,88 |
4,40 |
1,38 |
8,4 |
||
|
4 |
0,12 |
1,28 |
3,44 |
7,52 |
6,00 |
3,56 |
1,34 |
8,0 |
||
|
3 |
0,13 |
1,26 |
2,60 |
6,62 |
5,12 |
2,73 |
1,32 |
7,9 |
||
|
2 |
0,13 |
1,24 |
1,74 |
5,73 |
4 22 |
1,87 |
1,30 |
7,7 |
||
|
4,0 |
8 |
0,10 |
1,47 |
7,30 |
12,01 |
10,24 |
7,40 |
1,54 |
10,0 |
|
|
1 |
0,10 |
1,42 |
6,38 |
10,93 |
9,22 |
6,48 |
1,49 |
9,6 |
||
|
6 |
0,11 |
1,37 |
5,47 |
9,85 |
8,21 |
5,58 |
1,44 |
9,1 |
||
|
5 |
0,12 |
1,34 |
4,58 |
8,88 |
7,26 |
4,70 |
1,42 |
8,7 |
||
|
4 |
0,12 |
1,32 |
3,68 |
7,90 |
6,32 |
3,80 |
1,39 |
8,3 |
||
|
3 |
0,12 |
1,30 |
2,77 |
6,94 |
5,37 |
2,89 |
1,37 |
8,3 |
||
|
о |
0,12 |
1,29 |
1,86 |
5,99 |
4,44 |
1,98 |
1,35 |
8,3 |
||
|
4,5 |
8 |
0,Ю |
1,47 |
7,72 |
12,43 |
10,66 |
7,82 |
1,54 |
10,0 |
|
|
7 |
0,10 |
1,43 |
6,75 |
11,32 |
9,61 |
6,85 |
1,50 |
9,6 |
||
|
6 |
0,11 |
1,38 |
5,78 |
10,21 |
8,54 |
5,89 |
1,46 |
9,1 |
||
|
5 |
0,12 |
1,36 |
4,84 |
9,19 |
7,56 |
4,96 |
1,43 |
8,9 |
||
|
4 |
0,12 |
1,34 |
3,89 |
8,16 |
6,57 |
4,01 |
1,40 |
8,7 |
||
|
3 |
0,12 |
1,32 |
2,92 |
7,15 |
5,56 |
3,04 |
1,38 |
8,5 |
||
|
2 |
0,12 |
1,30 |
1,96 |
6,14 |
4,56 |
2,08 |
1,37 |
8,3 |
||
|
5,0 |
8 |
0,10 |
1,47 |
8,15 |
12,85 |
11,09 |
8,25 |
1,54 |
10,0 |
|
|
7 |
0,10 |
1 44 |
7,12 |
11,72 |
10,00 |
7,22 |
1,50 |
9,6 |
||
|
6 |
0,11 |
1,40 |
6,10 |
10,58 |
8,90 |
6,21 |
1,47 |
9,1 |
||
|
5 |
0,11 |
1,38 |
5,10 |
9,50 |
7,86 |
5,21 |
1,44 |
9,1 |
||
|
4 |
0,11 |
1,35 |
4,10 |
8,42 |
6,80 |
4,21 |
1,42 |
9,1 |
||
|
3 |
0,12 |
1,34 |
3,08 |
7,36 |
5,76 |
3,20 |
1,40 |
8,7 |
||
|
2 |
0,12 |
1,32 |
2,07 |
6,29 |
4,71 |
2,19 |
1,39 |
3,3 |
||
|
2,0 |
2,0 |
8 |
0,21 |
1,92 |
5,28 |
11,43 |
9,12 |
5,49 |
2,02 |
9.5 |
|
7 |
0,23 |
1,84 |
4,63 |
10,50 |
8,31 |
4,86 |
1,93 |
8,8 |
||
|
6 |
0,25 |
1,75 |
3,98 |
9,58 |
7,48 |
4,23 |
1,84 |
8.0 |
||
|
5 |
0,27 |
1,58 |
3,35 |
8,74 |
6,71 |
3,62 |
1,77 |
7,5 |
||
|
4 |
0,29 |
1,62 |
2,72 |
7,90 |
5,96 |
3,01 |
1,70 |
6.9 |
||
|
3 |
0,29 |
1,61 |
2,08 |
7,22 |
5,30 |
2,37 |
1,69 |
6.9 |
||
|
2 |
0,29 |
1,60 |
1,43 |
6,55 |
4,63 |
1,72 |
1,68 |
6,9 |
||
|
2,5 |
8 |
0,21 |
1,94 |
5,84 |
11,94 |
9,72 |
6,05 |
2,04 |
9,5 |
|
|
7 |
0,22 |
1,86 |
5,12 |
11,02 |
8,84 |
5,34 |
1,96 |
8,9 |
||
|
6 |
0,24 |
1,78 |
4,40 |
10,11 |
6,96 |
4,64 |
1,88 |
8,4 |
||
|
5 |
0,26 |
1,72 |
3,70 |
9,22 |
7,14 |
3,96 |
1,82 |
7,8 |
||
|
4 |
0,28 |
1,67 |
2,99 |
8,34 |
6,33 |
3,27 |
1,76 |
7,3 |
||
|
3 |
0,28 |
1,66 |
2,28 |
7,58 |
5,60 |
2,56 |
1,74 |
7,3 |
||
|
2 |
0,28 |
1,65 |
1,56 |
6,84 |
4,86 |
1,84 |
1,63 |
7,3 |
||
|
3,0 |
8 |
0,21 |
1,95 |
6,40 |
12,44 |
10,30 |
6,61 |
2,05 |
9,5 |
|
|
7 |
0,22 |
1,88 |
5,61 |
11,54 |
9,37 |
5,83 |
1,98 |
9,1 |
||
|
6 |
0,23 |
1,82 |
4,82 |
10,64 |
8,46 |
5,05 |
1,91 |
8,7 |
||
|
5 |
0,24 |
1,77 |
4,04 |
9,70 |
7,58 |
4,28 |
1,85 |
8,2 |
||
|
4 |
0,26 |
1 72 |
3,26 |
8,77 |
6,70 |
3,52 |
1,81 |
7,7 |
||
|
3 |
0,26 |
1,71 |
2,48 |
7,95 |
5,90 |
2,74 |
1,80 |
7,7 |
||
|
2 |
0,26 |
1,70 |
1,69 |
7,13 |
5,69 |
1,95 |
1,78 |
7,7 |
||
|
3,5 |
8 |
0,20 |
2,00 |
6,88 |
13,15 |
10,88 |
7,08 |
2,10 |
10,0 |
|
|
7 |
0,21 |
1,93 |
6,02 |
12,16 |
9,88 |
6,23 |
2,03 |
9,6 |
||
|
6 |
0,22 |
1,87 |
5,18 |
11,16 |
8,92 |
5,40 |
1,96 |
9,1 |
||
|
5 |
0,23 |
1,82 |
4,34 |
10,16 |
7,98 |
4,57 |
1,91 |
8,7 |
||
|
4 |
0,24 |
1,77 |
3,50 |
9,22 |
7,04 |
3,74 |
1,85 |
8,2 |
||
|
3 |
0,24 |
1,76 |
2,66 |
8,30 |
6,18 |
2,90 |
1,85 |
8,2 |
||
|
2 |
0,24 |
1,76 |
1,80 |
7,42 |
5,32 |
2,04 |
1,84 |
8,2 |
||
|
4,0 |
8 |
0,19 |
2,04 |
7,35 |
13,88 |
11,43 |
7,54 |
2,14 |
10,5 |
|
|
7 |
0,20 |
1,98 |
6,44 |
12,78 |
10,40 |
6,64 |
2,08 |
10,0 |
||
|
6 |
0,21 |
1,92 |
5,53 |
11,68 |
9,37 |
5,74 |
2,02 |
9,5 |
||
|
5 |
0,22 |
1,87 |
4,64 |
10,62 |
8,38 |
4,86 |
1,96 |
9,1 |
||
|
4 |
0,23 |
1,82 |
3,74 |
9,56 |
7,38 |
3,97 |
1,91 |
8,7 |
||
|
3 |
0,23 |
1,82 |
2,83 |
8,64 |
6,47 |
3,06 |
1,90 |
8,7 |
||
|
2 |
0,23 |
1,81 |
1,92 |
7,71 |
5,54 |
2,15 |
1,90 |
8,7 |
||
|
4,5 |
8 |
0,19 |
2,04 |
7,78 |
14,32 |
11,86 |
7,97 |
2,14 |
10,5 |
|
|
7 |
0,20 |
1,99 |
6,81 |
13,17 |
10,79 |
7,01 |
2,09 |
10,0 |
||
|
6 |
0,21 |
1,93 |
5,84 |
12,02 |
9,70 |
6,05 |
2,03 |
9,5 |
||
|
5 |
0,22 |
1,88 |
4,90 |
10,94 |
8,66 |
5,12 |
1,98 |
9,2 |
||
|
4 |
0,22 |
1,84 |
3,94 |
9,85 |
7,62 |
4,15 |
1,94 |
8,9 |
||
|
3 |
0,22 |
1,84 |
2,98 |
8,86 |
6,66 |
3,20 |
1,92 |
8,8 |
||
|
2 |
0,23 |
1,83 |
2,02 |
7,88 |
5,68 |
2,25 |
1,92 |
8,7 |
||
|
5,0 |
8 |
0,19 |
2,05 |
8,20 |
14,76 |
12,30 |
8,39 |
2,15 |
10,5 |
|
|
7 |
0,20 |
2,00 |
7,18 |
13,56 |
11,18 |
7,38 |
2,10 |
10,0 |
||
|
6 |
0,21 |
1,94 |
6,16 |
12,37 |
10,04 |
6,37 |
2,04 |
9,5 |
||
|
5 |
0,22 |
1.90 |
5,16 |
11,26 |
8,96 |
5,38 |
2,00 |
9,3 |
||
|
4 |
0 22 |
1,87 |
4,15 |
10,14 |
7,89 |
4,37 |
1,96 |
9,1 |
||
|
3 |
0,22 |
1,86 |
3,14 |
9,09 |
6,86 |
3,36 |
1,95 |
9,3 |
||
|
2 |
0,23 |
1,85 |
2,12 |
8,04 |
5,82 |
2,35 |
1,94 |
8,7 |
||
|
3,0 |
2,0 |
8 |
0,32 |
2,32 |
5,35 |
12,77 |
9,99 |
5.67 |
2,44 |
9,3 |
|
7 |
0,35 |
2,22 |
4,70 |
11,82 |
9,14 |
5,05 |
2,33 |
8,7 |
||
|
6 |
0,38 |
2,13 |
4,06 |
10,88 |
8,32 |
4,44 |
2,24 |
8,0 |
||
|
5 |
0,40 |
2,04 |
3,43 |
9,96 |
7,51 |
3,83 |
2,14 |
7,6 |
||
|
4 |
0,42 |
1,95 |
2,80 |
9,04 |
6,70 |
3,22 |
2,05 |
7,2 |
||
|
3 |
0,42 |
1,98 |
2,15 |
8,49 |
6,11 |
2,57 |
2,08 |
7,2 |
||
|
2 |
0,41 |
2,00 |
1,50 |
7,94 |
5,50 |
1,91 |
2,10 |
7,3 |
||
|
2,5 |
8 |
0,32 |
2,34 |
5,90 |
13,40 |
10,58 |
6,22 |
2,46 |
9,5 |
|
|
7 |
0,34 |
2,25 |
5,19 |
12,40 |
9,69 |
5,53 |
2,36 |
8,8 |
||
|
6 |
0,36 |
2,16 |
4,48 |
11,40 |
8,80 |
4,84 |
2,28 |
8,2 |
||
|
5 |
0,38 |
2,10 |
3,77 |
10,48 |
7,97 |
4,15 |
2,20 |
7,9 |
||
|
4 |
0,40 |
2,02 |
3,06 |
9,54 |
7,10 |
3,46 |
2,12 |
7,5 |
||
|
3 |
0,40 |
2,04 |
2,34 |
8,89 |
6,42 |
2,74 |
2,15 |
7,6 |
||
|
2 |
0,39 |
2,06 |
1,62 |
8,24 |
5,74 |
2,01 |
2,16 |
7,7 |
||
|
3,0 |
8 |
0,31 |
2,37 |
6,46 |
14,04 |
11,20 |
6,77 |
2,49 |
9,6 |
|
|
7 |
0,33 |
2,28 |
5,68 |
12,98 |
10,24 |
6,01 |
2,40 |
9,0 |
||
|
6 |
0,35 |
2,20 |
4,89 |
11,93 |
9,29 |
5,24 |
2,31 |
8,5 |
||
|
5 |
0,36 |
2,15 |
4,11 |
10,99 |
8,41 |
4,47 |
2,26 |
8,1 |
||
|
4 |
0,38 |
2,10 |
3,33 |
10,05 |
7,53 |
3,71 |
2,20 |
7,8 |
||
|
3 |
0,38 |
2,11 |
2,54 |
9,29 |
6,76 |
2,92 |
2,22 |
7,9 |
||
|
2 |
0,37 |
2,12 |
1,75 |
8,53 |
5,99 |
2,12 |
2,23 |
8,1 |
||
|
3,5 |
8 |
0,30 |
2,42 |
6,93 |
14,66 |
11,77 |
7,23 |
2,54 |
10,0 |
|
|
7 |
0,32 |
2,34 |
6,08 |
13,58 |
10,76 |
6,40 |
2,46 |
9,5 |
||
|
6 |
0,34 |
2,27 |
5,24 |
12,50 |
9,78 |
5,58 |
2,38 |
8,9 |
||
|
5 |
0,34 |
2,22 |
4,40 |
11,50 |
8,84 |
4,74 |
2,34 |
8,6 |
||
|
4 |
0,36 |
2,17 |
3,56 |
10,51 |
7,90 |
3.92 |
2,28 |
8,3 |
||
|
3 |
0,36 |
2,18 |
2,71 |
9,68 |
7,07 |
3,07 |
2,30 |
8,4 |
||
|
2 |
0,36 |
2,19 |
1,86 |
8,86 |
6,24 |
2,22 |
2,30 |
8,4 |
||
|
4,0 |
8 |
0,29 |
2,46 |
7,40 |
15.27 |
12,32 |
7,69 |
2,58 |
10,4 |
|
|
7 |
0,30 |
2,40 |
6,49 |
14,17 |
11,29 |
6,79 |
2,52 |
9,9 |
||
|
6 |
0,32 |
2,34 |
5,58 |
13,07 |
10,26 |
5,90 |
2,46 |
9,4 |
||
|
5 |
0,33 |
2,29 |
4,69 |
12,02 |
9,27 |
5,02 |
2,41 |
9,1 |
||
|
4 |
0,34 |
2,24 |
3,80 |
10,97 |
8,28 |
4,14 |
2,36 |
8,7 |
||
|
3 |
0,34 |
2,25 |
2.88 |
10,08 |
7,38 |
3,22 |
2,37 |
8,8 |
||
|
2 |
0,34 |
2,26 |
1,97 |
9,20 |
6,49 |
2,31 |
2,38 |
8,8 |
||
|
4,5 |
8 |
0,29 |
2,48 |
7,82 |
15,76 |
12,78 |
8.11 |
2,60 |
10,4 |
|
|
7 |
0,30 |
2,41 |
6,86 |
14,58 |
11,68 |
7,16 |
2,53 |
9,9 |
||
|
6 |
0,32 |
2,34 |
5,90 |
13,40 |
10,58 |
6,22 |
2,46 |
9,5 |
||
|
5 |
0,33 |
2,30 |
4,94 |
12,32 |
9,54 |
5,27 |
2,42 |
9,2 |
||
|
4 |
0 34 |
2,26 |
4,00 |
11,23 |
8,52 |
4,34 |
2,38 |
8,8 |
||
|
3 |
0,34 |
2,27 |
3,03 |
10.29 |
7,57 |
3,37 |
2,34 |
8,9 |
||
|
2 |
0,34 |
2,28 |
2,06 |
9,36 |
6,62 |
2,40 |
2,40 |
9,0 |
||
|
5,0 |
8 |
0,29 |
2,50 |
8,24 |
16,24 |
13,24 |
8,53 |
2,62 |
10,4 |
|
|
7 |
0,30 |
2,42 |
7,22 |
14,98 |
12,06 |
7,52 |
2,54 |
10,0 |
||
|
6 |
0,32 |
2,35 |
6,21 |
13,73 |
10,91 |
6.53 |
2,47 |
9,5 |
||
|
5 |
0,33 |
5,32 |
5,20 |
12,61 |
9,82' |
5,53 |
2,44 |
9,2 |
||
|
4 |
0,34 |
2,28 |
4,19 |
11,49 |
8,75 |
4,53 |
2,40 |
9,0 |
||
|
3 |
0,34 |
2,29 |
3,18 |
10,50 |
7,76 |
3,52 |
2,31 |
9,0 |
||
|
2 |
0,33 |
2,30 |
2,16 |
9,52 |
6,76 |
2,49 |
2,42 |
9,1 |
||
ПРИЛОЖЕНИЕ 32
Гидравлические данные для лотков на организованных руслах
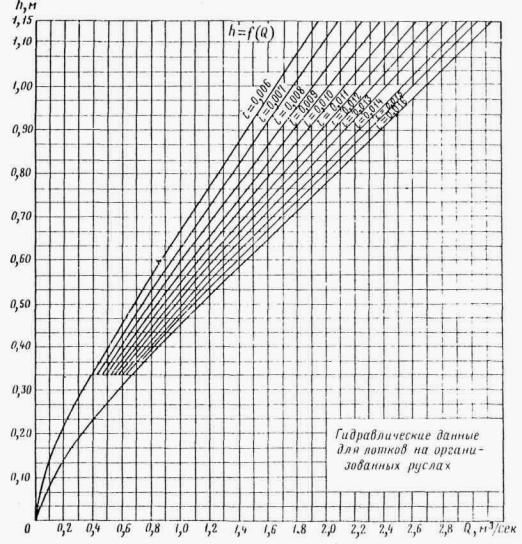
ПРИЛОЖЕНИЕ 33
Гидравлические данные для лотков на организованных руслах (инв.№ 160)
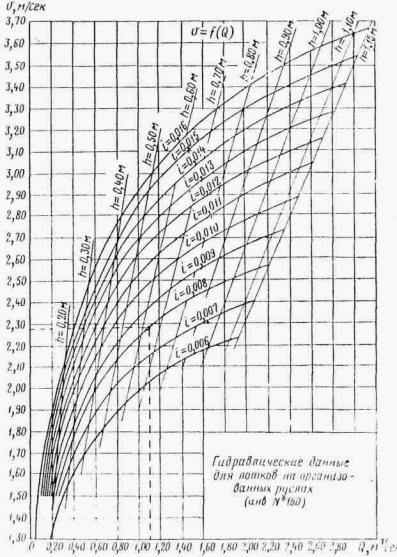
IIример. Дано Q = 1,1 м3/сек; l = 0,008; получаем v = 2,28 м/сек
ПРИЛОЖЕНИЕ 34
Гидравлические данные для лотков на неорганизованных руслах
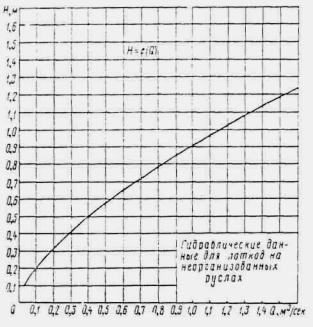
ПРИЛОЖЕНИЕ 35
Гидравлические данные для лотков на неорганизованных руслах (инв.№ 160)
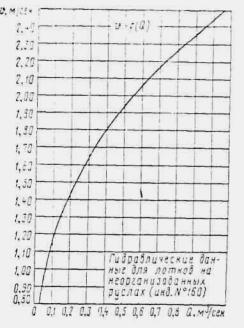
ЛИТЕРАТУРА
1. Чертоусов М.Д. Гидравлика (специальный курс). Госэнергоиздат, 1962.
2. Андреев О.В., Болдаков Е.В. и др. Краткий справочник по трубам и малым мостам. Автотрансиздат, 1963.
3. Богомолов А.И., Константинов Н.М. Примеры гидравлических расчетов. Автотрансиздат, 1962.
4. Андреев О.В., Болдаков Е.В. и др. Расчет отверстий искусственных сооружений по предельным состояниям. Автотрансиздат, 1963.
5. Агроскин И.И., Дмитриев Г.Т., Пикалов Ф.И. Гидравлика. М.-Л. Изд-во «Энергия», 1964.
6. Павловский Н.Н. Собрание сочинений, т. I. Р1 изд-во АН СССР, 1956.
7. Строительные нормы и правила. Часть II, раздел Д. Глава I. СНиП П-Д.1-62. Железные дороги колеи 1524 мм общей сети. Нормы проектирования. Стройиздат, 1964.
8. Строительные нормы и правила, часть II, раздел Д. СНиП П-Д.2-62. Железные дороги колеи 1524 мм промышленных предприятий. Стройиздат, 1963.
9. Строительные нормы и правила. Часть II. раздел Д. СНиП П-Д.5-62. Автомобильные дороги общей сети СССР. Стройиздат, 1964.
10. Строительные нормы и правила, часть II, раздел Д. СНиП П-Д.7-62. Мосты и трубы. Стройиздат, 1963.
11. Технические условия проектирования железнодорожных, автодорожных и городских мостов и труб. СН 200-62. Трансжелдориздат, 1962.
12. Временные нормы допускаемых скоростей течения воды в постоянных железнодорожных гидротехнических сооружениях. Трансжелдориздат, 1952.
13. Рабухин Л.Г. Сборный обтекаемый открылок к водопропускной трубе. Издание НТО ж.-д. транспорта, Тбилиси, 1966.
14. Рабухин Л.Г. О работе водопропускной трубы «с крышкой» на входном оголовке. «Известия высших учебных заведений. Строительство и архитектура», 1961, № 1.
15. Рабухин Л.Г. Исследование работы водопропускной трубы с горизонтальным козырьком над входным отверстием. «Автомобильные дороги», 1963, № 7.
16. Большаков В.А. и др. Сборник задач по гидравлике. Киев, «Будивельник», 1964.
17. Лиштван Л.Л. Об учете распластывания паводочной волны при проектировании малых мостов и труб. «Транспортное строительство», 1960, № 4.