Рекомендации Рекомендации по расчету и проектированию путепроводов на подрабатываемых территориях
|
Донецкий |
НИИ
строительных |
РЕКОМЕНДАЦИИ
по расчету и проектированию путепроводов
на подрабатываемых территориях
Донецк 1984
Рекомендованы к изданию решением ученого совета Донецкого Промстройниипроекта Госстроя СССР.
Рекомендации содержат основные положения по расчету и проектированию автодорожных и железнодорожных путепровод ов на подрабатываемых территориях II - IV групп.
Рассмотрены баллонные путепроводы с разрезными, температурно-неразрезными и неразрезными пролетными строениями. Приведены методики определения дополнительных усилий в конструкциях при вынужденных смещениях основания. Предложены конструктивные меры защиты путепроводов от влияния горных выработок. Даны примеры расчета.
Разработаны Донецким Промстройниипроектом Госстроя СССР (кандидаты техн. наук В.Р. Шнеер, А.И. Братанчук, инженеры А.А. Муха, И.Г. Коваль, О.А. Синюгин, И.И. Хитайлова), НИИСК Госстроя СССР (кандидаты техн. наук Н.С. Метелюк, И.А. Лукашенко, инж. С.А. Недодатко), Донецким филиалом Укркоммунниипроект МЖКХ УССР (инж. И.А. Федоренко), Донецким филиалом Укргипродор Миндорстроя УССР (инж. А. Н. Гладышева) под общей редакцией кандидатов техн. наук В.Р. Шнеера и Н.С. Метелюка.
Предназначены для инженерно-технических работников, занимающихся проектированием путепроводов на подрабатываемых территориях.
СОДЕРЖАНИЕ
|
I. Общие положения 2. РАСЧЕТ ПУТЕПРОВОДОВ КАК ПЛОСКИХ СТЕРЖНЕВЫХ СИСТЕМ 3. РАСЧЕТ ОПОР 4. ПРОСТРАНСТВЕННЫЙ РАСЧЕТ ПРОЛЕТНЫХ СТРОЕНИЙ 5. КОНСТРУКТИВНЫЕ РЕШЕНИЯ И МЕРЫ ЗАЩИТЫ ПУТЕПРОВОДОВ Приложение I ОПРЕДЕЛЕНИЕ ДЛИТЕЛЬНОЙ ЖЕСТКОСТИ ЖЕЛЕЗОБЕТОННЫХ ОПОР ПУТЕПРОВОДОВ Приложение 2 ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ЖЕСТКОСТИ ОСНОВАНИЯ Приложение 3 ПРИМЕРЫ РАСЧЕТА ПУТЕПРОВОДОВ
|
I. Общие положения
1.1. Настоящие Рекомендации предназначены для использования при проектировании автодорожных и железнодорожных путепроводов на подрабатываемых территориях II - IV групп.
1.2. Рекомендации содержат положения по расчету дополнительных усилий в конструкциях и их перемещений с учетом фактора времени, а также конструктивные меры защиты путепроводов от влияния горных выработок.
Воздействия подработки следует учитывать при расчете конструкций путепроводов на особые сочетания нагрузок.
1.3. Исходными данными при расчете конструкций путепроводов на воздействия, обусловленные влиянием горных выработок, являются:
объемно-планировочные и конструктивные решения объектов;
величины и характер постоянных нагрузок;
физико-механические характеристики грунтов основания;
величины и характер ожидаемых деформаций земной поверхности на участке строительства.
При расчете конструкций путепроводов с учетом фактора времени дополнительно следует учитывать длительность деформирования земной поверхности, изменение жесткостных характеристик железобетонных конструкций и основания.
В этом случае в качестве дополнительных исходных данных принимают:
условия изготовления железобетонных конструкций и возраст бетона к началу подработки сооружения;
сведения о климатических условиях в районе строительства; характеристики длительных деформативных свойств грунтов;
продолжительность деформирования основания от подработки.
1.4. Объемно-планировочные и конструктивные решения путепроводов, а также величины и характер постоянных нагрузок устанавливают по имевшейся проектной документации.
1.5. Физико-механические характеристики грунтов основания и обратных засыпок определяют, как правило, по данным полевых и лабораторных испытаний. При их отсутствии физико-механические характеристики грунтов допускается определять по данным соответствующих СНиП и СН.
1.6. Расчетные значения прочностных и деформационных характеристик грунтов при определении нагрузок, действующих на путепровод при сдвижении основания, должны приниматься равными нормативным.
1.7. Ожидаемые деформации земной поверхности на участке строительства определяют по маркшейдерским расчетам.
1.8. Продолжительность деформирования основания от подработки рекомендуется принимать равной общей продолжительности процесса сдвижения земной поверхности.
1.9. Изменение жесткостных характеристик железобетонных конструкций во времени от влияния ползучести бетона допускается не учитывать, если срок работы сооружения до начала подработки составляет, согласно указаниям прил. 3 СН 365-67, более трех лет.
1.10. В проекте путепровода, возводимого на подрабатываемой территории, рекомендуется предусматривать проведение работ, связанных с инструментальными наблюдениями за деформациями сооружения и окружающей его земной поверхности в период подработки.
2. РАСЧЕТ ПУТЕПРОВОДОВ КАК ПЛОСКИХ СТЕРЖНЕВЫХ СИСТЕМ
2.1. В качестве расчетных воздействий подрабатываемого основания принимают: относительную горизонтальную деформацию растяжения или сжатия ε и радиус кривизны выпуклости или вогнутости R.
Возможными сочетаниями воздействий от подработки являются:
горизонтальная деформация растяжения + ε и кривизна выпуклости + K ;
горизонтальная деформация сжатия - ε и кривизна вогнутости - K.
2.2. Расчетные вертикальные Δ hi , горизонтальные Δ li перемещения и наклоны Δφ i основания под фундаментами путепровода (рис. 1), обусловленные горизонтальными деформациями растяжения-сжатия и кривизны, определяют по формулам:
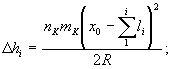 (1)
(1)
![]() (2)
(2)
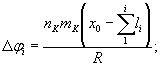 (3)
(3)
где nK и mK - коэффициенты перегрузки и условий работы для кривизны, принимаемые по СНиП II -8-78;
n ε и m ε - то же, для относительных горизонтальных деформаций;
x 0 - расстояние от центра тяжести подошвы фундамента нулевой опоры (устоя) до центра деформаций сооружения (НДС).
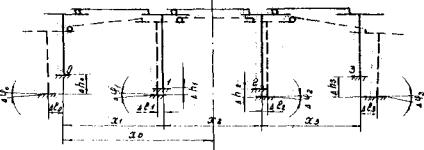
Рис. 1. К определению расчетных перемещений основания под фундаментами опор
2.3.Характер распределения и величины дополнительных усилий в конструкциях путепроводов, обусловленные неравномерными деформациями основания, зависят от жесткостных характеристик опор и основания, изменения этих величин во времени, типов фундаментов и опорных частей.
2.4. Для путепровода с разрезными пролетными строениями, опирающимися одним концом через шарнирно-неподвижные, а другим через шарнирно-подвижные опорные части, продольные усилия Xi и значение х0 определяют решением статически неопределимой рамы (рис. 2).
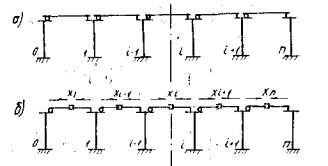
Рис. 2. К расчету путепровода с шарнирными опорными частями
а - расчетная схема; б - основная система метода сил
Система уравнений содержит канонические уравнения метода сил и дополнительное уравнение, определяющее ЦДС относительно нулевой опоры
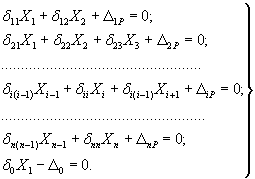 (4)
(4)
2.5. Единичные перемещения определяют по формулам:
δ i(i-1) = - δ 0 i -1 ; (5)
δ ii = δ 0 i -1 + δ 0 i ; (6)
δ i (i+1) = - δ 0 i , (7)
где δ0 i-1 и δ0 i - горизонтальные перемещения верха ( i-1)-й и i-й опор от единичной горизонтальной силы.
2.6. Единичное перемещение верха промежуточной опоры δ0 i определяют по формуле
δ 0 i = u0ci+u0ri, (8)
где u 0 ci - перемещение, обусловленное изгибом стоек, определяемое по формуле
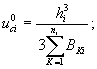 (9)
(9)
u0 ri - перемещение, обусловленное податливостью основания, определяемое по формуле (10) для опор с фундаментами на естественном основании и (11) - для опор со свайными фундаментами:
![]() (10)
(10)
![]() (11)
(11)
где hi - высота опоры (стойки) от обреза фундамента до верха ригеля;
ni - количество стоек i-й опоры;
B Ki - жесткость K-й стойки i-й опоры при изгибе в плоскости продольной оси путепровода;
Hi - высота опоры от подошвы фундамента до верха ригеля;
вф i - размер подошвы фундамента опоры в направлении продольной оси путепровода;
E и μ - соответственно модуль деформации и коэффициент Пуассона грунта, принимаемые средними в пределах сжимаемой толщи;
h в - коэффициент, принимаемый по прил. 3 СНиП II-16-74;
![]() и
и ![]() - горизонтальное
перемещение и угол поворота ростверка, определяемые согласно Руководству по
проектированию свайных фундаментов (М.: Стройиздат, 1980).
- горизонтальное
перемещение и угол поворота ростверка, определяемые согласно Руководству по
проектированию свайных фундаментов (М.: Стройиздат, 1980).
2.7. Единичное перемещение верха промежуточной опоры рекомендуется определять с учетом длительных деформативных свойств конструкции и основания по формуле
![]() (12)
(12)
где A ti - величина, определяемая по формуле
![]() (13)
(13)
fti - переменный во времени безразмерный коэффициент, вычисляемый по формуле
![]() (14)
(14)
В t пр i - приведенная жесткость i-й опоры, определяемая по прил. 1;
K t i - коэффициент жесткости основания i-й опоры, определяемый по прил. 2;
Dti - величина, определяемая по формуле
![]() (15)
(15)
Jф i - момент инерции подошвы фундамента i-й опоры в плоскости продольной оси путепровода.
2.8. Единичное перемещение верха крайней опоры (устоя) определяют при горизонтальных деформациях растяжения (+ ε) и сжатия (- ε) соответственно по формулам:
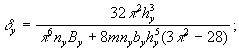 (16)
(16)
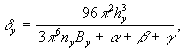 (17)
(17)
где α , β и γ - определяются по формулам:
α = 24m n у b y h y 4 (6 π 2 h ш + 3 π 2 hy -16 π h ш -28 hy ); (18)
β = 48 π 2 mhy 3 (2 h ш + h р y )( B ш - b y ny )h p y ; (19)
γ = 2 π 2 mB ш h у h 2 ш [4 hy (6 h у + π h ш ) + π h ш (4 h у + π h ш )]; (20)
h y - высота стойки устоя от обреза фундамента до верха ригеля;
bу - условная ширина стойки устоя в и, принимаемая равной bу = b+1 м для стоек шириной b ≥ 0,8 м и bу = 1,5 b+0,5 м - для остальных размеров сечения стоек;
Ву - жесткость стойки устоя при изгибе в плоскости продольной оси путепровода;
n у - количество стоек устоя;
hpy - высота ригеля устоя;
hш и Вш - высота и ширина шкафной стенки;
m - коэффициент пропорциональности для грунта, принимаемый по прил. 25 СН 200-62.
2.9. Единичное перемещение верха свайной опоры (промежуточной или устоя) определяют по формуле
![]() (21)
(21)
где h pi - высота ригеля (ростверка) опоры.
2.10. Вынужденные перемещения Δ i р в основной системе определяют по формуле
Δ ip = - Δ i -1 + Δ i , (22)
где Δ i - величины, определяемые по формуле
Δ i = Δl i +[ Hi + δ i ( N л + N п )] Δφ i , (23)
в которой Δ l i и Δφ i определяют по формулам ( 2) и ( 3),
N л и N п - опорные реакции от нормативной постоянной нагрузки пролетных строений, опирающихся на i -ю опору.
2.11. При расчете путепроводов с учетом фактора времени определение продольных усилий X i производится в процессе ряда последовательных приближений с уточнением на каждом этапе расчета жесткости опор. Практически достаточно выполнить трехкратное приближение.
Определение усилий Xi производится для расчетного момента времени t, рекомендации по определению которого приведены в прил. 1. Для дальнейшего расчета используются максимальные значения Xi.
2.12. Необходимо производить анализ величин X i, найденных в результате решения системы уравнений ( 4), путем сравнения максимального значения усилия с величиной силы трения, определяемой для K-го пролета, по формуле
T k = Nf, (24)
где N - опорная реакция от нормативной постоянной нагрузки;
f - коэффициент трения в подвижных опорных частях.
Если ХK ≤ Т K, полученные решением системы уравнений ( 4) значения являются окончательными. Если Х K > Т K, то расчет повторяют, полагая в системе уравнений ( 4) значение Х K равным по абсолютной величине TK, но с сохранением знака заменяемого усилия. Кроме того, в каноническом уравнении для K-го пролета в правую часть вместо нуля записывают неизвестное перемещение uK. В результате решения скорректированной системы уравнений ( 4) определяют усилия X 'i (за исключением k -го пролета, где это усилие равно Т K) и перемещение u' K. Выполняют анализ найденных усилий и в случае необходимости производят следующую корректировку системы уравнений ( 4). Расчет путепровода считается законченным, если максимальное усилие в пролете удовлетворяет условию Xmn ≤ Tm. Полученные в результате расчета значения X i n и u n i являются исходными при определении дополнительных усилий и перемещений в путепроводе от влияния горных выработок.
2.13. При расчете i-й опоры (см. рис. 2) учитывают: горизонтальные силы X i n и X n i +1 в пролетных строениях, опирающихся на i-ю опору;
эксцентриситет η uni +1 вертикальной нагрузки от (i+1)-го пролетного строения, опирание которого на i -ю опору является шарнирно-подвижным (при катковых опорных частях η = 0,5);
эксцентриситет приложения нагрузки от пролетных строений и собственного веса опоры, обусловленный ее креном, определяемым по формуле
![]() (25)
(25)
2.14. При проектировании деформационного шва над i -й опорой учитывают величину взаимного перемещения концов пролетных строений над этой опорой, равную uni +1 на эту же величину необходимо увеличить ширину ригеля i-й опоры.
2.15. Для путепровода с разрезными пролетными строениями, опирающимися обоими концами через деформируемые резиновые или слоистые опорные части (рис. 3), продольные усилия Х i и значение x0 определяют решением системы уравнений ( 4), в которой дополнительное уравнение, определяющее ЦДС относительно нулевой опоры, имеет вид
![]() (26)
(26)
Единичные перемещения δ i ( i -1) и δ i ( i +1) определяют по формулам ( 5) и ( 7), а δ ii - по формуле
δ ii = δ i (i-1) + δ 0 i +2 δ i p , (27)
где δ i p - единичное перемещение деформируемых опорных частей i-го пролета, вычисляемое по формуле
![]() (28)
(28)
hp - суммарная толщина слоев резины опорной части;
nр - количество опорных частей в поперечном направлении путепровода под одним из концов пролетного строения;
Fp - площадь горизонтального сечения опорной части;
Gр - модуль сдвига резины.
Единичные перемещения верха промежуточных опор и устоев определяют по пп. 2.6- 2.9 настоящих Рекомендаций.
Расчет выполняется методом попыток. Задаваясь положением ЦДС в k-м пролете, решают систему уравнений ( 4). Если найденное значение Х0 не соответствует расположению ЦДС в k-м пролете, то расчет повторяют, располагая ЦДС в другом пролете.
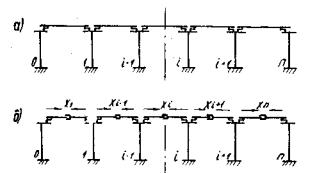
Рис. 3. К расчету путепровода с деформируемыми опорными частями
а - расчетная схема; б - основная система метода сил
2.16. Продольные усилия Xi в путепроводах с разрезными пролетными строениями, опирающимися обоими концами через деформируемые опорные части (см. рис. 3), рекомендуется определять с учетом фактора времени решением системы уравнений ( 4), в которой единичные перемещения δ i ( i -1) и δ i (+1) для промежуточных опор определяются по формулам ( 5), ( 7), ( 12), а величина δ ii - по формуле
![]() (29)
(29)
где A ' ti - величина, определяемая по формуле
A ' ti = ф ti hi ; (30)
f ' ti - безразмерный коэффициент, определяемый из выражения
![]() (31)
(31)
ф ti - величина, определяемая по формуле
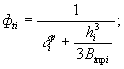 (32)
(32)
D ' ti - величина, определяемая по формуле
![]() (33)
(33)
δ p i - определяется по формуле ( 28).
При определении продольных усилий Xi с учетом фактора времени следует руководствоваться требованиями п. 2.11.
2.17. Полученные в результате расчета величины усилий не должны превышать предельного значения, определяемого по формуле
![]() (34)
(34)
В противном случае принимают опорные части с большей податливостью. Если и в этом случае условие Xi ≤ Хпр не удовлетворяется, то рекомендуется применить разгрузку опорных частей как меру защиты путепровода (см. разд. 5). При этом в качестве расчетных усилий принимают: в пролете с максимальным значением усилия Х K , найденного решением системы уравнений ( 4), Х K = Хпр в остальных пролетах
![]() (35)
(35)
2.18. При расчете i-й опоры путепровода с деформируемыми опорными частями (см. рис. 3) учитывают: горизонтальные силы Xi и Х i+1 ( X ' i и X ' i+1) в пролетных строениях, опирающихся на i-ю опору, а также эксцентриситет приложения нагрузок от пролетных строений и собственного веса опоры, обусловленный ее креном, вычисляемым по формуле ( 25), в которой вместо X n i и X n i+1 принимают Xi и Xi+1 (X 'i и X 'i+1).
2.19. Величина взаимного смещения концов пролетных строений над i-й опорой зависит от усилив в смежных пролетах и определяется по формуле
ui = δ p i Xi + δpi +1 Xi +1 , (36)
где X i и Xi+1 - усилия, найденные решением системы уравнений ( 4) или скорректированные согласно п. 2.18.
Для реализации найденных величин u i ширину ригеля i - й опоры увеличивают на 2 ui .
2.20. Для путепровода с температурно-неразрезными пролетными строениями и деформируемыми (резиновыми или слоистыми) опорными частями (рис. 4) продольные усилия Xi и значение Х0 определяют решением системы уравнение ( 4), в которой дополнительное уравнение, определяющее ЦДС относительно нулевой опоры, имеет вид
( δ 0 + δ р 1 ) X 1 - Δ 0 = 0. (37)
Единичные перемещения вычисляют по формулам:
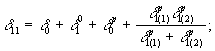 (38)
(38)
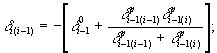 (39)
(39)
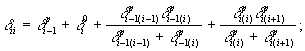 (40)
(40)
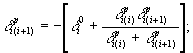 (41)
(41)
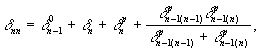 (42)
(42)
где δ p i ( i ) - единичное перемещение деформируемых опорных частей i -го пролета над i - й опорой;
δp i ( i + 1) - то же, ( i +1)-г o пролета.
2.21. Единичные перемещения рекомендуется определять с учетом фактора времени по формулам:
![]() (43)
(43)
![]() (44)
(44)
![]() (45)
(45)
![]() (46)
(46)
в которых A ' ti определяется по формуле ( 30) с учетом формулы (47).
Значение δ i i определяется по формуле ( 29), в которой величину Ф ti определяют из выражения
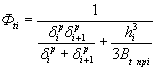 (47)
(47)
При определении продольных усилий X i с учетом фактора времени следует руководствоваться требованиями п. 2.11.
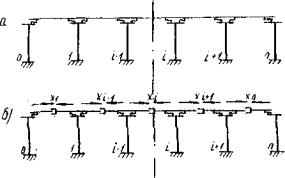
Рис. 4. К расчету путепровода с температурно-неразрезными пролетными строениями
а - расчетная схема; б - основная система метода сил
2.22. Полученные в результате расчета величины усилий в пролетных строениях должны удовлетворять требованиям, предъявляемым к деформациям опорных частей. Соответствующее условие для i-й промежуточной опоры имеет вид
![]() (48)
(48)
где δпр - меньшее из двух предельных значений для опорных частей i -го и (i+1)-го пролетов, равное 0,9 h p .
Если условие (48) не удовлетворяется, то необходимо принять опорные части с большей податливостью или предусмотреть их разгрузку (см. разд. 5). При этом в качестве расчетных усилий Q' i принимают:
для опоры с максимальным значение результирующего усилия Q K - предельную величину, определяемую по формуле
![]() (49)
(49)
для остальных промежуточных опор
![]() (50)
(50)
2.23. Кроме усилий Q i (или Q ' i) при расчете каждой промежуточной опоры учитывает эксцентриситет приложения нагрузок от пролетных строений и собственного веса опоры, обусловленный ее креном, определяемым по формуле
![]() (51)
(51)
2.24. Расчет и проектирование крайних опор (устоев) в путепроводах с температурно-неразрезными пролетными строениями выполняется аналогично их расчету и проектированию в разрезных путепроводах.
2.25. В случае применения разгрузки опорных частей опоры перемещаются относительно пролетного строения. Поэтому ширину ригеля каждой опоры принимают с учетом этих перемещений, определяемых по формуле
vi = Δ i - δ пр , (52)
где Δ i - величина, определяемая по формуле ( 23);
δ пр - то до, что и в формуле ( 48).
Ширину ригеля увеличивают с учетом влияния подработки на величину 2v i .
2.26. Путепроводы с неразрывными пролетными строениями на подрабатываемых территориях будут испытывать дополнительные усилия не только от горизонтальных перемещений Δ li наклонов Δφ i , но также и от неравномерных вертикальных перемещений оснований опор Δ hi .
2.27. Продольные усилия Х i и значение х0 в путепроводах с неразрезными пролетными строениями и деформируемыми (резиновыми или слоистыми) опорными частями (рис. 5) определяют решением системы уравнений ( 4), в которой дополнительное уравнение, определяющее ЦДС относительно нулевой опори, принимают в виде ( 37), а единичные перемещения вычисляют по формулам:
δ i (i-1) = -( δ 0 i -1 + δ p i -1 ); (53)
δ ii = δ0i-1+δ0i+δpi-1+δpi; (54)
δ i (I+1) = -(δ0i+δpi). (55)
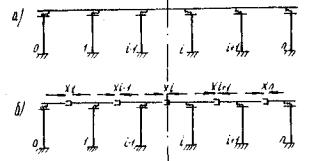
Рис. 5. К расчету путепровода с неразрезным пролетным строением
а - расчетная схема; б - основная система метода сил
2.28. Единичные перемещения рекомендуется определять с учетом фактора времени:
δ ii - по формуле ( 29), δi( i-1), δi( i-1) - по формулам:
![]() (56)
(56)
![]() (57)
(57)
При определении продольных усилий Xi с учетом фактора времени следует руководствоваться требованиями п. 2.11.
2.29. Результирующие горизонтальных усилий, действующие на опорные части, не должны превышать предельных значений, определяемых по формуле ( 34). В противном случае переходят на опорные части с большей податливостью или применяют разгрузку (см. разд. 5).
2.30. При расчете на неравномерные вертикальные перемещения основания Δ hi пролетные строения рассчитывают как неразрезные балки на упругих опорах.*
_________________________
* Клепиков С.Н. Расчет конструкций на упругом основании, Киев: Вуд i вельник,1967.
2.31. Рекомендуется выполнять проверку правильности решения системы уравнений ( 4). Полученные значения неизвестных должны удовлетворять уравнениям:
при расчете путепровода по п. 2.4
δ n Xn + Δ n =0; (58)
при расчете путепровода по п. 2.15
![]() (59)
(59)
при расчете путепроводов по п. п. 2.20, 2.27
(δ n + δpn ) Xn + Δ = 0. (60)
3. РАСЧЕТ ОПОР
3.1. Многостоечные опоры путепроводов (рис. 6) рекомендуется рассчитывать как статически неопределимые рамы на неравномерно деформируемом основании.
3.2. Расчет опор с фундаментами на естественном основании на воздействие горизонтальных деформаций производят согласно требованиям Руководства по проектированию зданий и сооружений на подрабатываемых территориях. Башенные, транспортные и заглубленные сооружения, трубопроводы (Донецкий Промстройниипроект, НИИСК, Донецк, 1982), а на воздействие кривизны - в соответствии с требованиями настоящих Рекомендаций.
Дополнительные усилия в многостоечных опорах со свайными фундаментами определяют с учетом совместного влияния горизонтальных деформаций и кривизны.
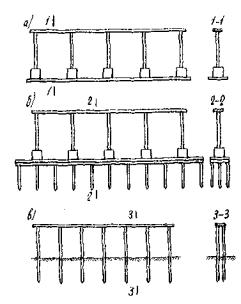
Рис. 6. Многостоечные опоры путепроводов
а - с фундаментами на естественном основании; б - со свайными фундаментами; в - свайные
3.3. Расчет опор рекомендуется производить в два этапа.
На первом этапе, используя принцип начала возможных перемещений, определяют, с учетом деформативности опоры и основания, значения реактивного отпора грунта по формуле
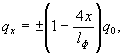 (61)
(61)
где q 0 - максимальное значение реактивного отпора грунта;
l ф - размер фундаментной плиты в плоскости опоры, а для опор со свайными фундаментами - расстояние между осями крайних свай;
х - текущая координата относительно края фундамента.
В формуле (61) знак «+» принимают при кривизне вогнутости, «-» - при кривизне выпуклости.
На втором этапе, считая реактивный отпор грунта внешней нагрузкой, методами строительной механики определяют дополнительные усилия в элементах рамы.
3.4. Максимальное значение реактивного отпора грунта определяют по формуле
![]() (62)
(62)
где k 0 - погонный коэффициент жесткости основания при сжатии;
η - максимальное значение разности оседаний земной поверхности под фундаментной плитой, вычисляемое по формуле
![]() (63)
(63)
z 1 - прогиб фундаментной плиты или свайного ростверка.
3.5. Погонный коэффициент жесткости основания при сжатии определяют по формулам:
для опор с фундаментами на естественном основании
![]() (64)
(64)
для опор со свайными фундаментами
![]() (65)
(65)
где kl - коэффициент, принимаемый по прил. 3 СНиП II-16-74;
B с,св - жесткость сваи при сжатии;
lN - длина сжатия сваи, определяемая по прил. 15 Руководства по проектированию свайных фундаментов (М.: Стройиздат, 1980);
dcв - расстояние между осями свай в плоскости опоры;
n - количество свай в ряду (в направлении, перпендикулярном плоскости опоры).
3.6. Значение z1 определяют решением системы линейных алгебраических уравнений:
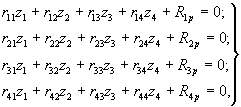 (66)
(66)
где rij - единичные реакции;
Rip - грузовые члены.
3.7. Единичные реакции rij системы уравнений (66) определяют по формулам:
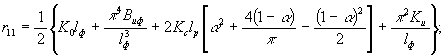 (67)
(67)
![]() (68)
(68)
![]() (69)
(69)
![]() (70)
(70)
r 22 = k0l ф + kclp (71)
![]() (72)
(72)
r 24 = r42 = -Kclp; (73)
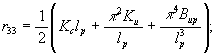 (74)
(74)
![]() (75)
(75)
r 44 = Kclp , (76)
где Виф и Вир - жесткости фундаментной плиты и ригеля;
K с и K и - коэффициенты, определяемые по формулам:
![]() (77)
(77)
![]() (78)
(78)
B с.ст и B и.cт - жесткости стойки при сжатии и изгибе;
l р - расстояние между осями крайних стоек опоры;
h ст - высота стойки;
d cт - расстояние между осями стоек;
α - коэффициент, определяемый по формуле
![]() (79)
(79)
В формулах ( 68), ( 70), ( 72) и ( 75) верхний знак принимается при кривизне вогнутости, нижний - выпуклости.
3.8. Грузовые члены R i p системы уравнений ( 66) определяют по формулам:
от горизонтальных деформаций сжатия и кривизны вогнутости:
![]() (80)
(80)
![]() (81)
(81)
от горизонтальных деформаций растяжения и кривизны выпуклости:
![]() (82)
(82)
![]() (83)
(83)
где h p - высота свайного ростверка.
В обоих случаях значения R3p - R 4р = 0.
В формулах (80) и (82) второе слагаемое учитывается только в опорах со свайными фундаментами, где Δ М 1 и Δ H 1 - дополнительные изгибающий момент и поперечная сила в голове крайней сваи, вызванные горизонтальными деформациями основания и определяемые в первом приближении без учета изгиба ростверка решением системы уравнений:
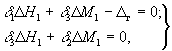 (84)
(84)
где δ 1 , δ 2 и δ 3 - единичные перемещения головы сваи от поперечной силы и изгибающего момента, определяемые по прил. 15 Руководства по проектированию свайных фундаментов (М. :Стройиздат, 1980);
Δ г - горизонтальное перемещение грунта, определяемое по формуле
![]() (85)
(85)
3.9. Рекомендуется выполнять проверку найденных значений z i по условиям:
при горизонтальных деформациях сжатия и кривизне вогнутости:
![]() (86)
(86)
![]() (87)
(87)
![]() при горизонтальных
деформациях растяжения и кривизне выпуклости:
при горизонтальных
деформациях растяжения и кривизне выпуклости:
![]() (88)
(88)
![]() (89)
(89)
3.10. Дополнительные изгибающий момент Δ Mi и поперечная сила Δ Н i в голове i - й сваи определяются решением системы уравнений:
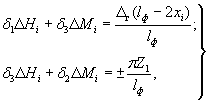 (90)
(90)
где x i - расстояние от I -й до i - й сваи.
Во втором уравнении системы (90) знак «+» принимают при кривизне вогнутости, «-» - при кривизне выпуклости.
3.11. Дополнительное продольное усилие в i - й свае определяют по формулам: при горизонтальных деформациях сжатие и кривизне вогнутости
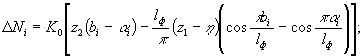 (91)
(91)
при горизонтальных деформациях растяжения и кривизне выпуклости
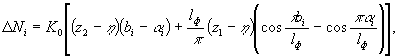 (92)
(92)
где bi и α i - расстояния, принимаемые равными: для первой сваи b 1 = 0,5dсв, α 1 = 0; для промежуточной сваи b i = ( i -0,5)dсв, α i =(i-1,5) d cв ; для n -й сваи bn = l ф , α n = l ф -0,5 d св .
3.12. Сумма дополнительных продольных усилий в сваях от воздействий горизонтальных деформаций и соответствующей им кривизны должна быть равна нулю
![]() (93)
(93)
где n cв - количество рядов свай в плоскости опоры.
3.13. Дополнительные усилия в голове i-й сваи свайной опоры определяют решением системы уравнений (90) и по формулам (91), (92), в которых значения z1 и z 2 определяют из системы уравнений:
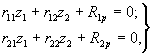 (94)
(94)
где r i j - единичные реакции, определяемые по формулам ( 67) и ( 68);
Rip - грузовые члены, определяемые по формулам ( 80) - ( 83).
3.14. Полученные значения дополнительных усилий в головах свай используют для определения дополнительных усилий в других расчетных сечениях согласно требованиям СНиП II-17-77.
4. ПРОСТРАНСТВЕННЫЙ РАСЧЕТ ПРОЛЕТНЫХ СТРОЕНИЙ
4.1. При расчете пролетного строения с учетом пространственной работы в качестве воздействия подрабатываемого основания принимают кривизну земной поверхности.
Расчетные величины неравномерных смещений смежных опор определяют для схемы расположения путепровода, при которой диагональ пролетного строения между этими опорами совпадает с направлением нормали к образующей кривизны земной поверхности (рис. 7).
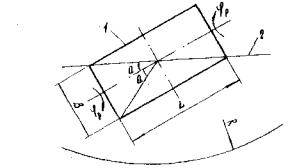
Рис. 7. К определению вертикальных перемещений пролетных строений при искривлении основания
1 - пролетное строение; 2 - нормаль к образующей кривизны земной поверхности
4.2. Значение тангенса угла поворота ригеля относительно его нулевой точки, лежащей на нормали к образующей кривизны земной поверхности, определяют по формуле
![]() (95)
(95)
где В - ширина пролетного строения;
α - угол между продольной осью и диагональю пролетного строения, вычисляемый по формуле
![]() (96)
(96)
L - длина пролетного строения между смежными опорами.
4.3. Линейные вертикальные перемещения заданных точек ригеля относительно его нулевой точки определяют по формуле
yi = α i tg φ p , (97)
где α i - расстояние от нулевой до i - й точки ригеля.
4.4. При расчете пролетного строения на неравномерные вынужденные вертикальные смещения опорных сечений принимают допущение о том, что балки (плиты) отделены друг от друга продольными сечениями, а распределение усилий между ними происходит не по всей длине пролетного строения, а только в нескольких задаваемых точках*. Рекомендуется делить пролет на 10 частей.
_______________
* Гибшман И.Е. Проектирование транспортных сооружений. М. :Транспорт, 1980.
4.5. В качестве неизвестных усилий в точках сопряжения плит проезжей части в продольных сечениях ребристого пролетного строений принимают изгибающие моменты mi и поперечные силы qi ( рис. 8), определяемые решением системы 2 rn канонических уравнений неразрывности деформаций
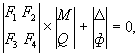 (98)
(98)
где F1, F 2 , F3, F 4 - блочные матрицы r -го порядка:
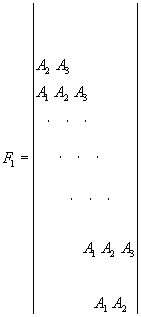 (99)
(99)
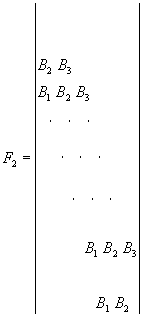 (100)
(100)
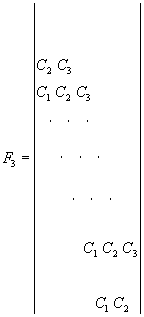 (101)
(101)
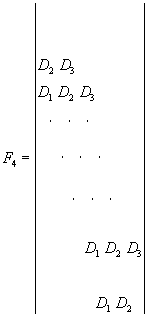 (102)
(102)
А 1 , А2, А3; В1, В2, В3; С1, С2, С3; D 1 , D 2 , D 3 - квадратные матрицы n -го порядка, образуемые соответственно элементами a jk 1 , a jk 2 , a jk 3 , b jk 1 , b jk 2 , b jk 3 , c jk 1 , c jk 2 , c jk 3 , d jk 1 , d jk 2 d jk 3 , например
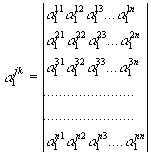 (103)
(103)
М и Q - блочные матрицы-столбцы:
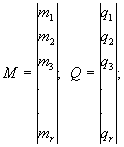 (104)
(104)
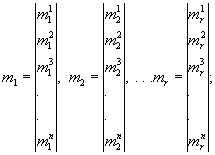 (105)
(105)
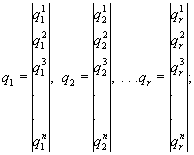 (106)
(106)
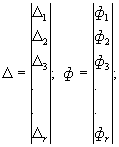 (107)
(107)
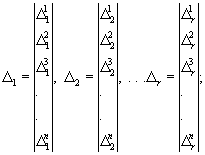 (108)
(108)
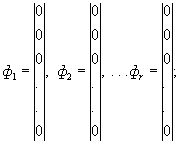 (109)
(109)
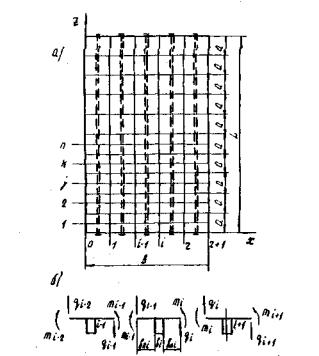
Рис. 8. Схема расчета ребристого пролетного строения
а - план; б - поперечное сечение
4.6. В системе канонических уравнений ( 98) коэффициентами при неизвестных являются перемещения основной системы, вызываемые единичными силами и моментами, действующими по направлениям отброшенных связей. Численные значения этих коэффициентов определяют по формулам:
α jk 1 ;= θ jk i (0,5 bi + bni ); (110)
![]() (111)
(111)
α jk 3 = - θ jk i+ 1 (0,5bi+1+bn(i+1)); (112)
bjk 1 ;= -fjki+ θ jk i (0,5bi+bni)2; (113)
![]() (114)
(114)
![]() (115)
(115)
с 1 jk = - θ i jk ; (116)
![]() (117)
(117)
с3 jk = - θ i+1 jk; (118)
d 1 jk = - θ jk i (0,5bi+bni); (119)
![]() (120)
(120)
d 3 jk = θ jk i+ 1 (0,5bi+1+bn(i+1)); (121)
где α 1 jk - линейное перемещение в поперечном сечении j по направлению силы qij от момента mki -1 , действующего в поперечном сечении k;
a 2 jk - то же, от момента mki = 1;
a 3 jk - то же, от момента mki +1 = 1;
b 1 jk - то же, от силы qki -1 = 1, действующей в поперечном сечении k ;
b 2 jk - то же, от силы qk i = 1;
b 3 jk - то же, от силы q k i +1 = 1;
c 1 j k - угол поворота в поперечном сечении j по направлению момента m j i от момента mki -1 = 1, действующего в поперечном сечении k;
c 2 j k - то же от момента mki = 1,
c 3 j k – то же от момента от момента mki +1 = 1;
d 1 j k - то же, от силы qki -1 = 1, действующей в поперечном сечении k ;
d 2 jk - то же, от силы qki = 1;
d 3 jk - то же, от силы qki +1 = 1;
fijk - вертикальное перемещение в см i - й балки в произвольном поперечном сечении j от вертикальной единичной силы, действующей в k -м сечении, определяемое с учетом кососимметричности расчетной схемы по формуле
![]() (122)
(122)
θ i jk - угол поворота i - й балки в произвольном поперечном сечении j от единичного момента, действующего в k -м сечении, определяемый по формуле
![]() (123)
(123)
L - пролет балки, см;
Fjk - коэффициент,
определяемый по табл. 1 в зависимости от относительных координат
рассматриваемого сечения ![]() и сечения
и сечения ![]() , в котором действует единичная сила;
, в котором действует единичная сила;
ujk - коэффициент,
определяемый по табл. 2 в зависимости от относительных координат
рассматриваемого сечения ![]() и сечения
и сечения ![]() в котором действует
единичный момент;
в котором действует
единичный момент;
J i - момент инерции на изгиб в поперечном направлении приведенного сечения участков плиты шириной α ;
J δ i - момент инерции приведенного сечения балки относительно его центра тяжести;
Jkp , i - момент инерции сечения балки при чистом кручении;
E - начальный модуль упругости бетона при сжатии и растяжении;
G - модуль упругости бетона при сдвиге;
Δ j i - взаимное смещение балок в точке пересечения сечений i и j (вертикальное перемещение ( i +1)-й балки относительно i-й балки в сечении j ), определяемое по формуле
![]() (124)
(124)
b 0 - расстояние между осями i - й и ( i +1)-й балок;
tgφр - тангенс угла поворота ригеля, определяемый по формуле ( 95).
Примечание. В формулах ( 111), ( 114), ( 117) и ( 120) последние два слагаемых равны нулю при всех значениях k , кроме - k = j.
Таблица 1
|
Zj / L |
Zk / L |
||||
|
0,05 |
0,15 |
0,25 |
0,35 |
0,45 |
|
|
0,05 |
1,62 |
3,50 |
3,70 |
2,74 |
0,98 |
|
0,15 |
3,50 |
8,82 |
9,90 |
7,38 |
2,70 |
|
0,25 |
3,70 |
9,90 |
12,50 |
9,90 |
3,70 |
|
0,35 |
2,70 |
7,38 |
9,90 |
8,82 |
3,50 |
|
0,45 |
0,98 |
2,74 |
3,70 |
3,50 |
1,62 |
Таблица 2
|
Zj /L |
Zk /L |
||||
|
0,05 |
0,15 |
0,25 |
0,35 |
0,45 |
|
|
0,05 |
0,045 |
0,035 |
0,025 |
0,015 |
0,005 |
|
0,15 |
0,035 |
0,105 |
0,075 |
0,045 |
0,015 |
|
0,25 |
0,025 |
0,075 |
0,125 |
0,075 |
0,025 |
|
0,35 |
0,015 |
0,045 |
0,075 |
0,105 |
0,035 |
|
0,45 |
0,005 |
0,015 |
0,025 |
0,035 |
0,045 |
4.7. При расчете плитного пролетного строения, устраиваемого из сборных балочных плит, шарнирно соединенных друг с другом, в качестве неизвестных усилий в продольных сечениях в местах шарниров принимают поперечные силы q 1 ( рис. 9), определяемые решением системы r n канонических уравнений неразрывности деформации
| F| ×| Q |+| Δ| = 0, (125)
где F - блочная матрица r -го порядка
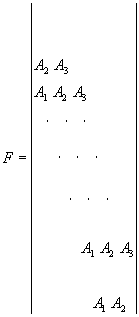 (126)
(126)
А 1 , А2 и А3 - квадратные матрицы n -го порядка, образуемые соответственно элементами а 1 jk , а 2 jk и а 3 jk например
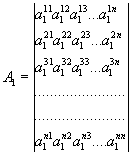 (127)
(127)
Q - блочная матрица-столбец
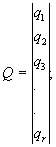 (128)
(128)
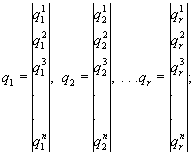 (129)
(129)
Δ - блочная матрица-столбец
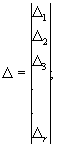 (130)
(130)
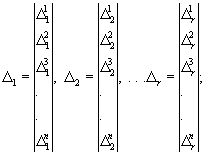 (131)
(131)
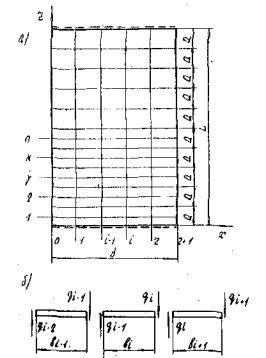
Рис. 9. Схема расчета плитного пролетного строения
а - план; б - поперечное сечение
4.8. В системе канонических уравнений ( 125) коэффициентами при неизвестных являются перемещения основной системы, вызываемые единичными силами, действующими по направлениям отброшенных связей. Численные значения этих коэффициентов определяют по формулам:
![]() (132)
(132)
![]() (133)
(133)
![]() (134)
(134)
где α 1 jk - линейное перемещение в сечении j по направлению силы qij от qi -1 k = 1, действующей в поперечном сечении k (учитываются податливость опорных частей, прогиб и закручивание балочной плиты);
α 2 jk - то же, от силы qik = 1;
α 3 jk - то же, от силы qi + 1 k = 1;
fijk - вертикальное перемещение i - й балочной плиты в произвольном поперечном сечении j от единичной силы, приложенной в k -м сечении, определяемое с учетом кососимметричности расчетной схемы согласно п. 4.9;
θijk - то же, угол поворота от единичного закручивающего момента, определяемый согласно п. 4.10;
Δ i j - взаимное смещение примыкающих продольных граней i -й и ( i +1)-й балочных плит в точке пересечения сечений i и j при неравномерном оседании опорных частей, определяемое согласно п. 4.11.
4.9. Вертикальное перемещение i - й балочной плиты в произвольном поперечном сечений / от единичной силы, приложенной в k -м сечении (рис. 10,а), определяют по формуле
fijk = fi,0jk+fi,ujk, (135)
где fi,0 jk - перемещение от деформации опорных частей, вычисляемое при ленточных и точечных деформируемых опорных частях соответственно по формулам:
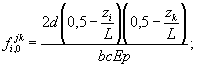 (136)
(136)
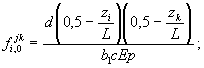 (137)
(137)
d - высота опорной части. Для слоистых резиновых опор ных частей принимается равной суммарной толщине слоев резины hp ;
b и b 1 - размер в направлении поперечной оси путепровода соответственно ленточной и точечной опорных частей;
с - размер опорной части в направлении продольной оси путепровода;
Ер - модуль упругости опорной части при осевом сжатии статистической нагрузкой;
Fi , u jk - перемещение от изгиба балочной плиты, вычисляемое по формуле (122).
4.10. Угол поворота i -й балочной плиты в произвольном поперечном сечении j от единичного закручивающего момента, приложенного в k-м сечении (см. рис. 10,б), определяет по формуле
θ i jk = θ i ,0 jk + θ i , kp jk , (138)
где θ i ,0 jk - угол поворота от деформации опорных частей, определяемый для случаев с ленточными и точечными деформируемыми опорными частями соответственно по формулам:
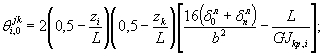 (139)
(139)
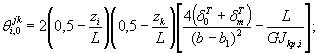 (140)
(140)
δ 0 - коэффициент, характеризующий податливость опорной части при сжатии, определяемый соответственно для ленточных и точечных опорных частей по формулам:
![]() (141)
(141)
![]() (142)
(142)
δ n - коэффициент, характеризующий податливость балочной плиты при скручиваний, определяемый соответственно при ленточных и точечных опорных частях по формулам
![]() (143)
(143)
![]() (144)
(144)
θ i , kp jk - угол поворота от скручивания балочной плиты, определяемый по формуле (123).
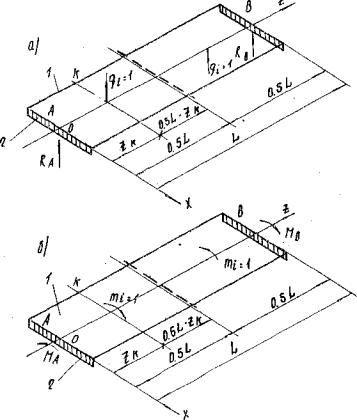
Рис. 10. Расчетные схемы балочной плиты
а - при загружении вертикальной силой; б - то же, закручивающим моментом; 1 - балочная плита; 2 - деформируемая опорная часть
4.11. Взаимное смещение примыкающих продольных граней смешных балочных плит в произвольном поперечном сечении определяют по формуле
![]() (145)
(145)
где Δ i ( i +1) - величина взаимного смещения примыкающих граней i-й и (i+1)-й плит в опорном сечении, определяемая по формуле
![]() (146)
(146)
где b - ширина балочной плиты;
tg φ p - тангенс угла поворота ригеля, определяемый по формуле ( 95);
δ 0 , δ n - коэффициенты, определяемые по формулам ( 141) или ( 142) и ( 143) или ( 144) соответственно для ленточных и точечных опорных частей.
4.12. При расчете пролетного строения на вынужденные смещения опор необходимо выполнять проверку наличия контакта балочных плит с спорными частями, являющимися односторонними связями плит с ригелем, соответственно при ленточных и точечных деформируемых опорных частях по условиям (147) и (148):
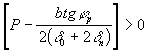 (147)
(147)
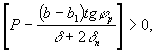 (148)
(148)
где Р - опорная реакция балочной плиты от постоянных нормативных нагрузок.
Если при определенных исходных данных в результате расчета балочных плит в основной системе условия (147) или (148) не удовлетворяются, то необходимо изменить исходные данные (понизить жесткость балочных плит при кручении или жесткость при сжатии деформируемых опорных частей) и повторить расчет. Система пригодна к эксплуатации при удовлетворении условий (147) или (148), т.е. когда нет вероятности нарушения контакта балочных плит пролетных строений с опорными частями.
5. КОНСТРУКТИВНЫЕ РЕШЕНИЯ И МЕРЫ ЗАЩИТЫ ПУТЕПРОВОДОВ
5.1. На подрабатываемых территориях II - IV групп рекомендуется применять балочные системы путепроводов с неразрезными, температурно-неразрезными и разрезными пролетными строениями.
При проектировании автодорожных путепроводов с пролетами до 20 м предпочтение следует отдавать плитным неразрезным и температурно-неразрезным конструкциям, а более 20 м - ребристым температурно-неразрезным конструкциям.
Для железнодорожных путепроводов рекомендуются ребристые разрезные конструкции пролетных строений.
Окончательный выбор типа пролетного строения производится на основании технико-экономического сравнения вариантов, разработанных с учетом настоящих Рекомендаций.
5.2. Исходными данными для назначения конструктивных мер защиты являются результаты расчетов дополнительных усилий в конструкциях и их перемещений, обусловленных влиянием подработки.
5.3. Защиту путепроводов рекомендуется производить по комбинированной схеме: усиление конструкции и обеспечение податливости их сопряжений в соответствии с результатами расчетов на воздействия от подработки.
5.4. При назначении конструктивных мер защиты путепроводов на подрабатываемых территориях следует ориентироваться на применение проверенных в практике Мостостроения конструкций и узлов этих сооружений,
5.5. Опоры путепроводов рекомендуется применять многостоечные рамные с фундаментами на естественном основании.
5.6. Пазухи котлованов под фундаменты рекомендуется заполнять материалами с низким модулем деформаций с целью улучшения условий работы опор при горизонтальных перемещениях и наклонах основания.
5.7.Армирование железобетонных стоек опор и фундаментов на дополнительные, усилия, обусловленные деформационными воздействиями подрабатываемого основания, следует принимать симметричным.
5.8. Ширину ригеля опоры необходимо увеличивать согласно расчету путепровода как плоской стержневой системы на воздействие горизонтальных деформаций и кривизны земной поверхности.
5.9. В качества опорных частей автодорожных путепроводов рекомендуется применять деформируемые опорные части, обладающие всесторонней податливостью, что создает наиболее благоприятные условия для пространственной работы пролетных строений.
5.10. Для расширения области применения деформируемых опорных частей в автодорожных путепроводах на подрабатываемых территориях рекомендуется, по мере достижения опорными частями предельных деформаций на какой-либо опоре, производить их разгрузку путем кратковременного минимального подъема пролетного строения над опорой.
5.11. Для установки гидравлических домкратов необходимо на боковых поверхностях ригелей предусматривать опорные столики или закладные детали для последующей приварки столиков (при отдаленных сроках подработки). Количество опорных столиков (или закладных деталей) и их размещение на боковых поверхностях ригеля принимают в зависимости от типа пролетного строения (ребристое или плитное), величины нагрузки от собственного веса пролетного строения, а также предполагаемой грузоподъемности гидравлических домкратов.
5.12. При соответствующем обосновании допускается предусматривать разгрузку деформируемых опорных частей при помощи инвентарных устройств для подъема пролетных строений.
5.13. Если проектом путепровода предусматривается разгрузка опорных частей, то он должен содержать указания по технологии подъема пролетных строений. Подъем необходимо производить синхронно по обе стороны от опоры, на которой производится разгрузка опорных частей. С этой целью все домкраты, участвующие в разгрузке опорных частей на данной опоре, объединяют в одну гидросистему с механической или ручной (для небольших путепроводов) насосной станцией.
5.14. Конструкции деформационных швов автодорожных путепроводов принимают в зависимости от расчетных величин перемещений пролетных строений. Для путепроводов с разрезными пролетными строениями рекомендуется существующая номенклатура типов швов.*
_____________________________
* Шестериков В.И, Деформационные швы в автодорожных мостах. - М.: Транспорт, 1978.
Для путепроводов с неразрезными и температурно-неразрезными пролетными строениями, наряду с существующими, предлагается конструктивное решение деформационного шва на устое с заменяемыми плитами (рис. 11).
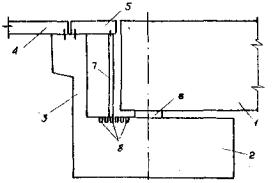
Рис. 11. Конструкция деформационного шва на устое
1 - пролетное строение; 2 - ригель; 3 - шкафная стенка; 4 - переходная плита; 5 - заменяемая плита; 6 - опорная часть; 7 - переставные стойки; 8 - отверстия для фиксации стоек
5.15. Для железнодорожных путепроводов на подрабатываемых территориях рекомендуется применение массивных опор, включающих средства регулирования, обеспечивающие возможность устранения крена опор и компенсации горизонтальных смещений основания.
5.16. Конструкция регулируемой опоры показана на рис. 12. Опора 1, жестко связанная с подколенником 2, опирается на опорную пяту 3, свободно лежащую на поверхности фундамента 4. По периметру подколенника со стороны, прилегающей к опорной пяте, устраивают ниши 5 для размещения гидравлических домкратов, служащих для рихтовки опоры по вертикали с целью устранения крена. Возможность отделения подколонника от опорной пяты достигается устройством между ними разделительного шва 6.
Между прилегающими поверхностями опорной пяты 3 и обреза фундамента 4 выполняют шов скольжения 7. Для фиксации пяты от горизонтальных смещений при эксплуатации путепровода используют консольные упоры 8 и инвентарные железобетонные вкладыши 9. При необходимости рихтовки опоры по горизонтали вкладыши 9 удаляют, а в пространстве между боковыми поверхностями опорной пяты и консольными упорами горизонтально размещают гидравлические домкраты.
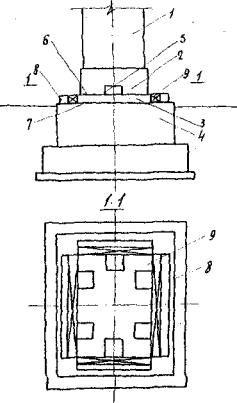
Рис. 12. Конструкция регулируемой массивной опоры
1 - опора; 2 - цокольная часть опоры; 3 - опорная пята; 4 - фундамент; 5 - домкратная ниша; б - разделительный шов; 7 - шов скольжения; 8 - консольные упоры; 9 - инвентарные вкладыши
5.17. Размеры и количество домкратных ниш в подколеннике определяют по условиям размещения гидравлических домкратов грузоподъемностью 100 или 200 т, суммарная грузоподъемность которых должна не менее чем в 1,3 раза превышать вертикальную постоянную нагрузку в уровне разделительного шва.
5.18. Величину горизонтальной силы, необходимой для смещения опоры, определяют по формуле
T = hKT p Nc , (149)
где h - коэффициент запаса по шву, принимаемый равным 2;
K tp - коэффициент трения, принимаемый в зависимости от конструкции шва скольжения по СНиП II-8-78.
Nc - постоянная вертикальная нагрузка в уровне разделительного шва.
5.19. Шов скольжения рекомендуется выполнять из двух слоев листового полиэтилена с прослойкой графита. Плоскость шва должна быть выровнена с таким расчетом, чтобы отклонения его размеров по вертикали не превышали 5 мм на 1 м2 поверхности шва.
5.20. Консольные упоры рассчитывают на действие силы Т. В зависимости от требуемого количества гидравлических домкратов упоры могут выполняться отдельно под каждый домкрат или в виде ленты. Расстояние между боковыми поверхностями опорной пяты и консольными упорами принимают в соответствии с расчетной величиной компенсации горизонтальных смещений основания.
5.21. Все железобетонные конструкции регулируемой опоры, контактирующие с гидравлическими домкратами, рассчитывают на местное сжатие. Нагрузку от домкратов рекомендуется передавать через стальные плиты размером 250 × 250 мм и толщиной не менее 20 мм.
5.22. Расчет регулируемой опоры на устойчивость положения против опрокидывания производят для горизонтального сечения в уровне разделительного шва.
5.23. Конструкция рельсового пути на железнодорожном путепроводе должна обеспечивать возможность его рихтовки при неравномерных оседаниях основания. С этой целью путь рекомендуется проектировать на щебеночном балласте, а ширину пролетного строения принимать с учетом расчетной величины подъема пути и наращивания балласта.
Приложение I
ОПРЕДЕЛЕНИЕ ДЛИТЕЛЬНОЙ ЖЕСТКОСТИ ЖЕЛЕЗОБЕТОННЫХ ОПОР ПУТЕПРОВОДОВ
1. Жесткость внецентренно сжатых железобетонных сечений стоек опор путепроводов определяется с учетом ползучести бетона в расчетный момент времени t по формуле
В t = E δ J п p mt , (1)
где E δ - начальный модуль упругости бетона, определяемый согласно СНиП II-21-75;
J пр - приведенный момент инерции поперечного сечения стойки относительно нейтральной оси, определяемый по формулам (2), (3) настоящего приложения;
mt - коэффициент изменения жесткости во времени, определяемый согласно п. 3 настоящего приложения. За расчетный момент времени t принимается момент, численно равный общей продолжительности деформирования основания от подработки.
2. Приведенный момент инерции симметрично армированного железобетонного сечения стойки на участках без трещин в растянутой зоне определяется с учетом растянутой зоны бетона по формуле
![]() (2)
(2)
где J δ - момент инерции бетонного сечения;
n - величина, определяемая по формуле
![]() (3)
(3)
E α - модуль упругости арматуры;
x - высота сжатой зоны сечения, определяемая из выражения (8) с учетом рекомендаций п. 4 настоящего приложения;
F α - площадь арматуры, расположенной у одной из противоположных граней сечения, перпендикулярных плоскости действия изгибающего момента.
Приведенный момент инерции на участках с трещинами определяется без учета растянутой зоны бетона по формуле
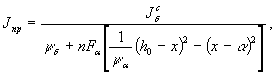 (4)
(4)
где J δ c - момент инерции сжатой зоны бетона;
ψδ - коэффициент, определяемый согласно требованиям СНиП II-21-75;
ψα - коэффициент, определяемый согласно требованиям СНиП II-21-75 при кратковременном действии длительно действующей части силовых нагрузок совместно с деформационными воздействиями.
3. Коэффициент изменения жесткости сечения на участках стоек, работающих без трещин, определяется по формуле
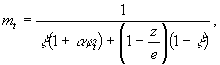 (5)
(5)
где φ t - характеристика ползучести бетона в расчетный момент времени t, определяемая согласно требованиям прил. 3 СН 365-67 (за начало нагружения принимается момент времени, в который появляются деформационные воздействия от подработки);
α - коэффициент, принимаемый по таблице настоящего приложения;
z - плечо внутренней пары, вычисляемое по формуле
z = h0-0,33x; (6)
е - эксцентриситет приложения внешней продольной силы N в сечении относительно центра тяжести растянутой арматуры, определяемый по формуле
![]() (7)
(7)
ξ - относительная высота сжатой зоны сечения, определяемая по формуле
![]() (8)
(8)
h - высота сечения стойки в плоскости действия изгибающего момента;
е н - начальный эксцентриситет приложения внешней продольной силы N в сечении относительно центра тяжести растянутой арматуры, определяемый по формуле
![]() (9)
(9)
е 0 - начальный эксцентриситет внешней силы N относительно центра тяжести сечения;
Mg - дополнительный изгибающий момент в сечении, вызванный деформационными воздействиями от подработки.
|
φ t |
æ |
||||||||||
|
0,00 |
0,05 |
0,10 |
0,15 |
0,20 |
0,25 |
0,30 |
0,35 |
0,40 |
0,45 |
0,50 |
|
|
0,1 |
1,00 |
0,95 |
0,90 |
0,86 |
0,83 |
0,79 |
0,76 |
0,73 |
0,70 |
0,68 |
0,66 |
|
0,5 |
1,00 |
0,94 |
0,89 |
0,84 |
0,80 |
0,76 |
0,73 |
0,69 |
0,67 |
0,64 |
0,61 |
|
1,0 |
1,00 |
0,93 |
0,86 |
0,81 |
0,77 |
0,73 |
0,69 |
0,65 |
0,62 |
0,59 |
0,56 |
|
1,5 |
1,00 |
0,92 |
0,85 |
0,79 |
0,74 |
0,69 |
0,65 |
0,61 |
0,58 |
0,55 |
0,52 |
|
2,0 |
1,00 |
0,91 |
0,83 |
0,76 |
0,71 |
0,66 |
0,61 |
0,58 |
0,54 |
0,51 |
0,48 |
|
1,5 |
1,00 |
0,90 |
0,81 |
0,74 |
0,68 |
0,63 |
0,58 |
0,54 |
0,51 |
0,48 |
0,45 |
|
3,0 |
1,00 |
0,89 |
0,80 |
0,72 |
0,66 |
0,60 |
0,56 |
0,51 |
0,48 |
0,45 |
0,42 |
Примечания: 1. Величина æ = n μ x , где ![]()
2. Для промежуточных значений φ t и æ коэффициент α определяется линейной интерполяцией.
На участках с трещинами коэффициент mt определяется по формуле
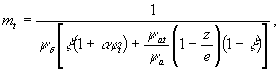 (10)
(10)
где φ at - коэффициент, определяемый согласно требованиям СНиП II-21-75 при длительном действии силовых нагрузок совместно с деформационными воздействиями.
4. Относительная высота сжатой зоны симметрично армированного сечения стойки, работающей без трещин в растянутой зоне, определяется по формуле
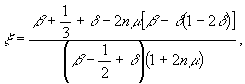 (11)
(11)
где β , δ , μ - величины, определяемые по формулам
![]()
b - ширина сечения стойки.
На участках с трещинами относительная высота сжатой зоны определяется из решения уравнения
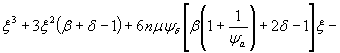 (12)
(12)
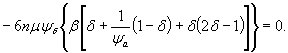
5. Момент трещинообразования для сечений стоек опор автодорожных путепроводов определяется в соответствии с требованиями СНиП II-21-75. Расчет по образованию трещин в опорах железнодорожных путепроводов, подверженных воздействию многократно повторной нагрузки, производится в соответствии с требованиями СНиП II-21-75. Максимальные растягивающие напряжения в бетоне определяются согласно СH 365-67 и СНиП II-21-75.
6. Жесткость сечений железобетонных стоек опор при расчете на деформационные воздействия от подработки допускается принимать постоянной по высоте и равной условной приведенной жесткости сечения, определяемой по формуле
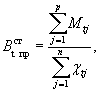 (113)
(113)
где Mt j - наибольший изгибающий момент на j-м участке высоты стойки в расчетной момент времени t, где он условно принимается постоянным по высоте j -го участка. Рекомендуется разбивать стойку по высоте не менее чем на пять участков (р = 5);
χ tj - кривизна оси j -го участка стойки, определяемая по формуле
![]() (14)
(14)
Bt j - жесткость сечения j-го участка, определяемая согласно п. 1 настоящего приложения.
7. Приведенная жесткость i - й опоры определяется по формуле
![]() (15)
(15)
где m - количество стоек в опоре;
В t пр. k - приведенная жесткость k -й стойки, определяемая по формуле (13) настоящего приложения.
8. Дополнительные усилия в стойках опоры, возникающие
от деформационных воздействий, вызванных подработкой, распределяются пропорционально величинам их приведенных жесткостей.
9. Учитывая, что жесткость сечений опоры зависит от действующих внутренних усилий, определение приведенной жесткости опор и дополнительных усилий в них производится путем последовательных приближений. На первом этапе расчета величину Mt допускается принимать с учетом Mg , полученного из упругого расчета, на последующих - Mt определяется как сумма изгибающего момента от длительно действующей части силовых нагрузок и дополнительного М g , найденного на предыдущем этапе.
Приложение 2
ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТОВ ЖЕСТКОСТИ ОСНОВАНИЯ
1. Длительный коэффициент жесткости основания в расчетный момент времени t определяется по формуле
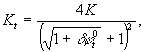 (I)
(I)
где K - условно-мгновенный коэффициент жесткости линейно-деформируемого основания, определяемый по прил. 2 СНиП II-8-78;
δ - безразмерный коэффициент, зависящий от гибкости фундамента, принимаемый для жестких фундаментных конструкций равным 1;
φ t 0 - обобщенная характеристика длительного деформирования (ползучести) грунтов основания при сжатии.
2. Обобщенная характеристика длительного деформирования грунтов основания при сжатии определяется по данным штамповых испытаний по формуле
φ t 0 = φ∞ 0 ut , (2)
где φ ∞ 0 - предельное значение характеристики, определяемое по формуле
![]() (3)
(3)
S ∞ - полная условно-стабилизированная осадка основания при длительности испытаний 7-10, 15, 20-25 сут соответственно для сильно-, средне- и малосжимаемых грунтов;
S 0 - условно-мгновенная, осадка, определяемая не более чем через 5 с. после статического приложения нагрузки;
ut - функция характеризующая длительность деформирования основания, определяемая в момент времени t по прил. 2 СНиП II-8-78.
3. Для предварительной оценки влияния длительных деформативных свойств грунтов на напряженно-деформированное состояние путепроводов при подработке величина коэффициента жесткости основания определяется по указаниям прил. 2 СНиП II-8-78.
Приложение 3
ПРИМЕРЫ РАСЧЕТА ПУТЕПРОВОДОВ
Пример 1
Определить дополнительные усилия и перемещения в конструкциях путепровода от воздействий подрабатываемого основания
Исходные данные: проектируется трехпролетный путепровод с разрезными пролетными строениями, деформируемыми опорными частями, многостоечными опорами и фундаментами на естественном основании (рис. 1); параметры опор: нулевая опора (устой): h y =7 м, Ну = 8,3 м, b = 0,4 м, b у = 1,1 м, h py = 0,5 м, h ш = 1,44 м, Вш = 9,8 м, n у = 4, Ву = 18,14 × 107 Па м4; первая и вторая опоры: h 1 = h 2 = 7 м, H1 = H2 = 8,3 м, b ф 1 = b ф 2 = 2,8 м, l ф 1 = l ф 2 = 9,6 м, n 1 = n 2 = 4, В1 = B 2 = 10,5 × 107 Па м4; третья опора (устой): hy = 6,5 м, Ну = 7,8 м, b = 0,4 м, by = 1,1 м, hpy = 0,5 м, h ш = 1,08 м, Вш = 9,8 м, n у = 4, Ву = 18,14 104 Па м4; параметры опорных частей: типа РОЧСП 30 × 40-8,9 для пролетных, строений длиной 21 м: h p = 0,065 м, np = 5, Fp = 0,12 м2, G р = 106 Па, типа РОЧСП 30 × 40-3,3 для пролетного строения длиной 12 м: h p = 0,025 м, n = 5, F р = 0,12 м2, G р = 106 Па; опорные реакции пролетных строений от нормативной постоянной нагрузки: Nоп = 159,13 104 Н, Н1л = Н1п = 159,13 104 Н, Н2л = 159,13 104 Н, N 2п = 83,36 104 Н, N 3л = 83,36 104 Н; характеристики грунта основания: Е = 1,8 107 Па, μ = 0,2; конусы насыпи подходов отсыпаны из мелких песков, для которых, согласно прил. 25 СН 200-62, m = 5 106 Н/м4; ожидаемые деформации земной поверхности: относительные горизонтальные деформации растяжения - сжатия ε = 4 10-3, радиус кривизны выпуклости - вогнутости R = 10 км.
1. Определяем единичные перемещения верха опор.
Опора 0. При горизонтальных деформациях растяжения по формуле ( 16)
![]()
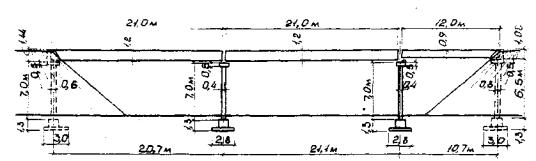
Рис. 1. Схема путепровода
Для определения δ при горизонтальных деформациях сжатия предварительно по формулам ( 18) - ( 20) вычислим:
α = 24 × 5 × 106 × 4 × 1,1 × 74(6 × 3,142 × 1,44+3 × 3,142 × 7-16 × 3,14 × 1,44-28 × 7) = 3028982,6 · 107 Н · м2;
β = 48 × 3,142 × 5 × 106 × 73(2 × 1,44+0,5)(9,8-4 × 1,1) × 0,5 = 802036,9 × 107 Н · м2;
γ = 2×3,142×5×106×9,8×7×1,442[4×7(6×7+3,14×1,44)+3,14×1,44(4×7+3,14×1,44)] =
= 2033020,5×107 Н · м2.
По формуле ( 17)
![]()
Опоры 1 и 2. По формуле ( 8) с учетом формул ( 9) и ( 10)
![]()
Опора 3. При горизонтальных деформациях растяжения по формуле ( 16)
![]()
Для определения δ y при горизонтальных деформациях сжатия предварительно по формулам ( 18)-( 20) вычислим:
α = 24 × 5 × 106 × 4 × 1,1 ×6,5 4 (6 × 3,142 × 1,08+3 × 3,142 ×6,5 -16 × 3,14 × 1,08-28 ×6,5 ) =
= 1874658,3×107 Н · м2;
β = 48 × 3,142 × 5 × 106 ×6,5 3 (2 × 1,08+0,5)(9,8-4 × 1,1) × 0,5 = 466719,6 × 107 Н · м2;
γ = 2×3,142×5×106×9,8×6,5×1,082[4×6,5(6×6,5+3,14×1,08)+3,14×1,08(4×6,5+3,14×1,08)] =
= 880379,0×107 Н · м2.
По формуле ( 17)
![]()
2. Определяем единичные перемещения деформируемых опорных частей по формуле ( 28):
для первого и второго пролетов
![]()
для третьего пролета
![]()
3. Определяем вынужденные перемещения фундаментов путепровода.
При горизонтальных деформациях растяжения и кривизне выпуклости по формуле ( 23) с учетом формул ( 2) и ( 3) вычисляем:
![]()
![]()
![]()
![]()
![]()
Вынужденные перемещения в основной системе по формуле ( 22):
Δ 1р = -0,004001х0+0,004125х0-0,085383 = 0,000124х0-0,085383;
Δ2 р = -0,004125х0+0,085383+0,004095х0-0,171168 = 0,00003х0-0,085765;
Δ 3р = -0,004095х0+0,171167+0,003962х0-0,211967 = -0,000133х0-0,0408.
При горизонтальных деформациях сжатия и кривизне вогнутости по формуле ( 23) с учетом формул ( 2) и ( 3) вычисляем:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Вынужденные перемещения в основной системе по формуле ( 22):
Δ 1р = 0,004х0-0,004125х0+0,085385 = -0,000125х0+0,085385;
Δ2 р = 0,004125х0-0,085385-0,004095х0+0,171168 = 0,00003х0+0,085783;
Δ 3р = 0,004095х0-0,171168-0,003961х0+0,211968 = 0,000134х0-0,04075.
4. Определяем единичные перемещения по формулам ( 5), ( 7) и ( 27).
При горизонтальных деформациях растяжения и кривизне выпуклости
δ 11 = (0,201690+5,132368+2×1,063333)×10-7 = 7,500724×10-7 м/Н;
δ 33 = (5,132368+0,221061+2×0,416667)×10-7 = 6,186763×10-7 м/Н.
При горизонтальных деформациях сжатия и кривизне вогнутости:
δ 11 = (0,053462+5,132368+2×1,083333)×10-7 = 7,352496×10-7 м/Н;
δ 33 = (5,132368+0,075775+2×0,416667)×10-7 = 6,041477×10-7 м/Н.
Остальные единичные перемещения б обоих случаях будут одинаковы:
δ 12 = δ21 = -5,132368×10-7 м/Н;
δ 22 = 2×(5,132368+1,083333)×10-7= 12,431402×10-7 м/Н;
δ 23 = δ32 = -5,132368×10-7 м/Н.
5. Задаемся положением ЦДС в третьем пролете. Тогда дополнительное уравнение ( 26) системы уравнений ( 4) примет вид:
при горизонтальных деформациях растяжения и кривизне выпуклости
0,201690×10-7х1+2×1,083333×10-7(х1+х2)+0,416667×10-7х3-0,004001х0 = 0
или, после приведения,
2,368356×10-7+2,166666×10-7+0,416667×10-7-0,0,40001 = 0;
при горизонтальных деформациях сжатия и кривизне вогнутости
2,220128×10-7х1+2,166666-10-7х2+0,416667×10-7х3+0,004х0 = 0.
6. Составляем систему уравнений ( 4).
При горизонтальных деформациях растяжения и кривизне выпуклости
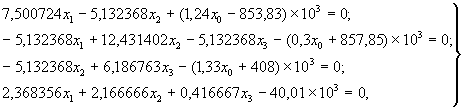
откуда х1 = 371221,3 Н; х2 = 387541,2 Н; х3 = 397566,3 Н; х0 = 47,1 м.
При горизонтальных деформациях сжатия и кривизне вогнутости
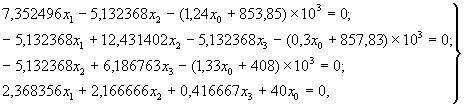
откуда x1 = -392132 Н; х2 = -407140,2 Н; х3 = -424065 Н; х0 = 48,235 м.
7. Выполняем проверку правильности решения системы уравнений ( 4) по уравнению ( 59):
при горизонтальных деформациях растяжения и кривизне выпуклости
(0,221061+0,416667)×10-7×397566,3+0,003962×47,1-0,211967 = 0;
при горизонтальных деформациях сжатия и кривизне вогнутости
-(0,075775+0,416667)×10-7×424065-0,003961×48,235+0,211918 = 0.
8. Проверяем выполнение требования п. 2.17.
При горизонтальных деформациях растяжения и кривизне выпуклости соответственно в 1, 2 и 3-м пролетах:
![]()
![]()
![]()
При горизонтальных деформациях сжатия и кривизне вогнутости максимальное усилие в 3-м пролете
Х 3 = 424065 Н < Хпр = 540000 Н.
9. Определяем величины взаимных смещений концов пролетных строений над опорами по формуле ( 36).
При горизонтальных деформациях растяжения и кривизне выпуклости
u 0 = 1,083333×10-7×371221,3 = 0,04 м;
u 1 = 1,083333×10-7×(371221,3+387541,2) = 0,082 м;
u 2 = 1,083333-×10-7×387541,2+0,416667×10-7×397566,3 = 0,059 м;
u 3 = 0,416667×10-7×397566,3 = 0,017 м
При горизонтальных деформациях сжатия и кривизне вогнутости
u 0 = 1,083333×10-7×|-392132 | = 0,042 м;
u 1 = 1,083333×10-7×|-392132-407140,2| = 0,087 м;
u 2 = 1,083333×10-7×|-407140,2|+0,416667×10-7×|-424065| = - 0,062 м;
u 3 = 0,416667×10-7×424065 = 0,018 м.
Пример 2
Определить дополнительные усилия в конструкциях опоры путепровода от воздействия кривизны основания
Исходные данные: проектируется многостоечная опора с фундаментами на естественном основании (рис. 2); жесткостные характеристики элементов опоры: Виф = 457×106 Па м4, Вир = 1188,5×106 Па м4, Вс.ст = 8542,9×106 Па м2, Ви.ст = 183,74×106 Па м4; характеристика грунта основания: Е =3,5×107 Па, μ = 0,17; ожидаемый радиус кривизны вогнутости земной поверхности R = 3 км.
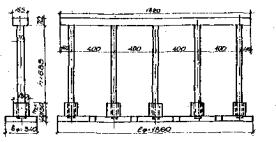
Рис. 2. Многостоечная опора
1. Определяем максимальное значение разности оседания земной поверхности под фундаментной плитой по формуле ( 63)
![]()
2. Определяем погонный коэффициент жесткости основания по формуле ( 64)
![]()
3. Определяем коэффициенты K с и K и по формулам ( 77) и ( 78):
![]()
![]()
4. Определяем коэффициент α по формуле ( 79)
![]()
5. Определяем единичные реакции по формулам ( 67)-( 76):
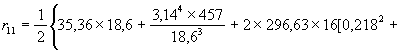
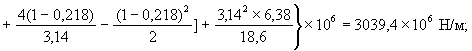
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
6. Определяем грузовые члены по формулам ( 80) и ( 81):
![]()
![]()
7. Решением системы уравнений ( 66)
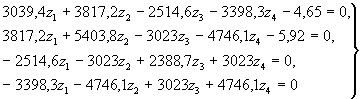
определяем значение z1 = 0,0117 м, z 2 = 0,00155 м, z 3 = 0,00883 м, z4 = 0,0043 м.
8. Выполняем проверку найденных значений zi по условиям ( 86) и ( 87)
![]()
![]()
9. Определяем максимальное значение реактивного отпора грунта по формуле ( 62)
![]()
10. Записываем выражение для определения значений реактивного отпора грунта как функцию от x :
![]()
11. Выполняем расчет многостоечной опоры как рамы на действие реактивной нагрузки.
Эпюра дополнительных изгибающих моментов в опоре от воздействия кривизны земной поверхности показана на рис. 3.
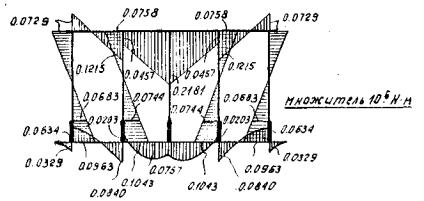
Рис. 3. Эпюра дополнительных изгибающих моментов в опоре