Рекомендации Рекомендации по выбору методов расчета коэффициента устойчивости склона и оползневого давления
МИНИСТЕРСТВО МОНТАЖНЫХ И
СПЕЦИАЛЬНЫХ
СТРОИТЕЛЬНЫХ РАБОТ УССР
УКРГЛАВСПЕЦСТРОЙ
УКРСПЕЦСТРОЙПРОЕКТ
РЕКОМЕНДАЦИИ
ПО ВЫБОРУ МЕТОДОВ РАСЧЕТА
КОЭФФИЦИЕНТА УСТОЙЧИВОСТИ СКЛОНА
И ОПОЛЗНЕВОГО ДАВЛЕНИЯ
Центральное бюро научно-технической информации
Москва - 1986
Рекомендации по выбору методов расчета коэффициента устойчивости склона и оползневого давления разработаны на основе анализа существующих способов расчета, сравнения их применительно к практическим вычислениям, а также экспериментальных исследований, выполненных специально для разработки настоящих рекомендаций.
В работе проанализированы существующие способы расчета, усовершенствованы их конечные формулы, приведены рекомендации по рациональной области использования каждого метода, по способам учета действия грунтовых вод и сейсмических воздействий, а также по принципам построения эпюры оползневого давления.
Рекомендации предназначены для инженерно-технических работников проектных и строительных организаций.
Рекомендации разработаны канд. техн. наук Л.К. Гинзбургом.
УСЛОВНЫЕ ОБОЗНАЧЕНИЯ
γ, γ i - удельный вес грунта (индекс « i » обозначает номер рассматриваемого отсека из всех, на которые условно разбит оползневой блок);
γ ч - удельный вес твердых частиц грунта;
γск - удельный вес скелета (вес твердой фазы в единице объема грунта);
W - влажность грунта в процентах;
γω - удельный вес воды;
n - пористость грунта;
γв, γв i - удельный вес грунта, взвешенного в во де;
γбр - удельный вес грунта, полностью насы щенного водой (без взвешивания);
e - коэффициент пористости грунта;
ci , φi - удельное сцепление и угол внутреннего трения (параметры сопротивления сдвигу или сдвиговые характеристики) в уровне подошвы отсека (по поверхности скольжения в данном отсеке);
c в i , φ в i - сдвиговые характеристики грунта в замоченном состоянии;
σ ni - нормальное напряжение в рассматриваемой точке отсека;
F р i = tg φi + ci / σni - коэффициент сопротивления сдвигу;
Ψ р i = arctg F р i - угол сдвига;
H - высота склона по вертикали;
β - угол наклона поверхности склона к горизонту;
li - длина подошвы или основания отсека (длина плоской поверхности скольжения в пределах отсека или длина хорды, соединяющей границы подошвы отсека);
L - длина линии скольжения для всего рассматриваемого участка склона;
ai - длина отсека по горизонтали в плоско сти чертежа;
h ср. i - средняя толщина оползневого грунта в рассматриваемом отсеке;
V - объем грунта;
α i - угол наклона подошвы отсека к горизонту (угол наклона плоской поверхности скольжения в пределах отсека, а в случае криволинейной поверхности скольжения - угол наклона хорды, соединяющей границы подошвы отсека);
Ωi - площадь подошвы отсека;
b - ширина оползневого блока в плоскости, перпендикулярной чертежу;
hi - гидравлический напор в отсеке (средняя высота водонасыщенной части отсека);
ωi = a i / hi - площадь сечения потока грунтовых вод в данном отсеке (в плоскости чертежа);
β ф i - уклон кривой депрессии (угол наклона к горизонту равнодействующей гидродинамического (фильтрационного) давления);
i = sin β ф i - гидравлический градиент (падение гидравлического напора на единицу длины в направлении течения);
Pi - полный вес одного из отсеков, на которые разбивается оползневой блок (с учетом внешней временной и постоянной нагрузок, находящихся в пределах отсека);
P в i - вес отсека с учетом взвешивания водой;
Ni = Pi cos αi - нормальная составляющая веса отсека;
Qi = Pi sin αi - сдвигающая сила (касательная составляющая веса отсека);
Ti = Ni tg φi - сила трения;
C i = cili - сила сцепления (при принятии b = 1,0);
Ri = Ti + Ci = Ni tg φi + cili = Pi cos αi tg φi + cili - суммарная удерживающая касательная сила (сопротивление перемещению i -го отсека по поверхности скольжения);
ji - фильтрационная сила (гидродинамическое давление) в i -ом отсеке;
Ei - результирующее давление от одного отсека;
E оп - суммарное оползневое давление сползающего блока;
K у - коэффициент запаса устойчивости склона (фактический коэффициент устойчивости);
K у э - задаваемый коэффициент устойчивости (для укрепляемого склона);
Q с , Q с i - сейсмическая сила.
ПРЕДИСЛОВИЕ
Вследствие освоения под строительство территорий, которые раньше считались непригодными, все чаще приходится возводить здания и сооружения на косогорах и неустойчивых склонах. При этом, кроме задач обеспечения надежности возводимых корпусов, требуется решать вопросы сохранения окружающей среды и экономного использования территории. В решениях XXVII съезда КПСС, в новой Конституции СССР, а также в принятом ЦК КПСС и Советом Министров СССР постановлении «О дополнительных мерах по усилению охраны природы и улучшению использования природных ресурсов» указывается на необходимость разработки и осуществления мероприятий по охране окружающей среды, более экономного использования свободных земель при строительстве промышленных и гражданских сооружений.
В связи с этим вопрос рационального проектирования и строительства на неустойчивых склонах в настоящее время приобрел наиболее актуальное значение. Для организаций Министерства монтажных и специальных строительных работ, которые не только возводят специальные сооружения на оползнеопасных территориях, но также занимаются проектированием и строительством самих противооползневых конструкций, вопрос достоверной оценки степени устойчивости склона является особенно важным.
Однако четких рекомендаций о том, какими методами следует оценивать степень устойчивости склона, на котором необходимо вести строительство, а также какие способы применять для определения давления на противооползневое сооружение, в настоящее время в нормативной литературе не существует. Разбросанные по большому количеству литературных источников методы расчета нередко весьма противоречивы и трудно применимы для практических вычислений.
Поэтому в настоящих рекомендациях проанализированы основные из существующих методов расчета, сделаны выводы о том, для каких условий какие методы целесообразнее применять. Кроме того, все методы расчета приведены к формам, удобным для практического применения.
Простота выведенных конечных формул позволит пользоваться ими не только проектным организациям, но также и монтажным специализированным управлениям и трестам, которым нередко требуется оперативно оценить степень устойчивости склона, на котором необходимо устанавливать механизмы и производить специальные и монтажные работы.
Кроме целей выбора наиболее рациональных способов расчета, анализ существующих методов позволит, во-первых, ознакомить проектировщиков и строителей с существующим уровнем знаний по данному вопросу, во-вторых, использовать ими способ оценки устойчивости склонов параллельно различными методами (что дает большую достоверность оценки), в-третьих, благодаря настоящим рекомендациям, выбрать из всех существующих именно те методы, которые в каждом конкретном случае помогут получить наиболее верный результат.
В работе приведены существующие способы расчета коэффициента устойчивости склона и величины оползневого давления в преобразованном (для удобства применения) виде, разработаны рекомендации по способам учета грунтовых вод и сейсмических воздействий, произведено сравнение различных методов расчета и даны рекомендации по областям применения каждого из них, а также по способам построения эпюры оползневого давления, необходимой для проектирования противооползневых конструкций.
I . ИСХОДНЫЕ ПОЛОЖЕНИЯ
1.1 . Основные предпосылки
При проектировании любых противооползневых мероприятий, при строительстве на неустойчивых склонах или при размещении механизмов на откосах, склонах или бортах оврагов работы следует начинать с оценки степени устойчивости наклонной поверхности земли. Такая оценка производится путем вычисления так называемого коэффициента устойчивости, который характеризуется отношением сил, удерживающих массив грунта на наклонной поверхности, к силам, сдвигающим этот массив. Для проектирования противооползневых мероприятий нередко требуется еще определять величину давления грунта от смещающегося массива на ограждающую конструкцию (оползневое давление). Для таких вычислений существует очень большое количество расчетных методов, которые, по существу, не регламентированы нормативными документами.
Большинство из существующих методов расчета устойчивости склонов было разработано для вычисления коэффициента устойчивости склона. Затем эти расчеты (как правило, автором данной работы) преобразовывались для определения так называемого оползневого давления, т.е. давления, передающегося от неустойчивых грунтовых масс оползневого склона. При этом для расчета противооползневых удерживающих конструкций разработаны способы построения эпюры оползневого давления по протяженности оползня.
Все расчетные методы оценки степени устойчивости склонов основаны на применении теории предельного равновесия, рассматривающей предельное напряженное состояние грунтового массива. В расчетной модели принимается ряд условных допущений:
используется гипотеза затвердевшего тела (призма возможного смещения рассматривается в виде затвердевшего клина);
рассматривается узкая полоса склона шириной 1 м; условия ее работы сохраняются для всего склона;
допускается определенная форма поверхности скольжения;
при пользовании основным критерием прочности (τ = s tg φ + c ) напряжения заменяются силами;
в некоторых методах силы взаимодействия между отсеками, на которые разбивается оползневой блок, не учитываются;
принимаются излагаемые далее допущения о значениях и проявлениях давления грунтовых вод и сейсмической силы;
в некоторых методах при рассмотрении равновесия массива принимается одно уравнение статики;
в отдельных случаях теория предельного равновесия применяется к грунтовому массиву, находящемуся в запредельном состоянии (при K у < 1).
Несмотря на перечисленные допущения и исходя из необходимости охватить как можно больше встречающихся на практике случаев (разнородное геологическое сложение склонов, наличие грунтовых вод, воздействие сейсмических сил и т.д.), эти методы расчета, хотя и не вполне математически и физически строгие, необходимы для разработки простых инженерных способов оценки устойчивости склонов и откосов.
При расчетах оползневого давления положение наиболее опасной поверхности скольжения, как правило, принимается уже установленным. Существует множество натурных и теоретических методов установления поверхности скольжения. Из натурных необходимо отметить следующие методы: визуального наблюдения за проходимыми при бурении скважин и шурфов породами - по зеркалам и штрихам скольжения, по повышенной влажности грунтов и т.д.; глубинного репера из отрезков труб (Е.П. Емельяновой); глубинного шлангового репера; глубинного репера с электрическим фиксатором смещений. (И.Я. Баранова); обратного поплавкового отвеса; метод М.Н. Рубаника; динамического и статического зондирования (определение поверхности скольжения по областям с пониженным сопротивлением перемещению зонда); длительного наблюдения за относительным смещением колец, которыми обсажена наблюдательная скважина, и др. Из теоретических можно отметить методы Б.М. Ломизе, И.В. Федорова [ 26], Г.М. Шахунянца [ 38, 39], Г.Л. Фисенко и др.
Нередко поверхность скольжения предопределена самим геологическим строением склона, например, когда покровные грунты (делювий) сползают по коренным породам. Однако в таких случаях к анализу следует подходить с осторожностью. Если коренными породами являются полускальные грунты (аргиллиты, алевролиты, известняки, и т.д.), то поверхность скольжения может проходить и выше, и ниже кровли таких пород. В окончательном виде для упрощения расчетов поверхность скольжения принимается в виде простейших форм - из ломаных линий, из дуг окружности и т.д.
Положение поверхности скольжения, так же как и значения прочностных характеристик грунтов ( c и φ ), установленные по материалам инженерно-геологических изысканий, следует при практическом проектировании уточнять обратными расчетами, исходя из значения коэффициента устойчивости склона, приблизительно соответствующего его значению при фактическом состоянии склона (при неустойчивом положении склона K у ≈ 1). При этом, в соответствии с результатами исследований многих советских ученых (М.Н. Гольдштейн, Э .М. Добров, Ю.К. Зарецкий, Н.Н. Маслов, Г.И. Тер-Степанян, А.Я. Туровская, Н.А. Цытович и др.), значения сдвиговых характеристик грунтов на уровне поверхности скольжения могут быть снижены вследствие возможного изменения их во времени с учетом ползучести. Такое снижение прочностных свойств грунтов (особенно глинистых) в некоторых условиях может быть значительным, что необходимо учитывать при проектировании.
Для практических расчетов возможно применять метод учета реологических свойств грунтов, разработанный проф. Н.Н. Масловым [ 15]. Как известно, по Н.Н. Маслову сопротивляемость грунта сдвигу представляется выражением:
sp ω = p tg φω + Σω + c с , ( 1)
где p - действующее в породе по данной площадке нормальное напряжение;
φω - угол внутреннего трения при влажности W ;
Σω - связность породы водно-коллоидной природы и обратимого характера при влажности W ;
c с - жесткое структурное сцепление с характером необратимых связей.
Ползучесть проявляется, когда действительные сдвигающие напряжения τ лежат в пределах
p tg φω + c с < τ < p tg φω + Σω + c с . ( 2)
В таком случае прочность грунта обеспечивается на тот или иной период, однако в связи с деформацией ползучести возможно нарушение необратимого сцепления c с во времени с общим падением прочности грунта.
В реологическом анализе весьма важным оказывается расчленение присущего глинистому грунту общего сцепления с на слагающие его обратимое Σω и необратимое c с сцепления. Этот анализ выполняется путем сопоставления значений сопротивления породы сдвигу в монолите и при сдвиге «плашек» породы по искусственно подготовленной поверхности. Затем проводится длительное испытание на сдвиг с контролируемой деформацией под действующей нагрузкой τ для определения возможного снижения значений φω , Σω и c с во времени и характеристик вязкости грунта.
По методике Н.Н. Маслова может быть выполнен прогноз скорости перемещения вниз по склону оползневых масс на длительный период и интенсивности деформаций смещения подпорных сооружений.
В случаях, когда по материалам инженерно-геологических изысканий и имеющихся теоретических методов положение наиболее опасной поверхности скольжения установить не удается, расчетные методы оценки устойчивости склонов в прямом виде применить не представляется возможным. В таких случаях следует использовать вариационные методы расчета, предложенные А.Д. Гиргидовым, М.Н. Гольдштейном, А.Г. Дорфманом, У.Х. Магдеевым и др.
При расчетах устойчивости склона или оползневого давления сползающий грунтовый блок членится вертикальными линиями на ряд отсеков. Обычно отсеки принимаются такими, чтобы без потери точности можно было в их пределах принимать поверхность за плоскость, а состояние грунта, очертание склона, действие внешних сил и т.п. практически однородными. Как правило, ширина отсеков не должна превышать 5 - 6 м.
Введем допущение относительно точки приложения и направления равнодействующей оползневого давления. Если оползневое давление считать активным, то, по мнению автора, схема его распределения по высоте аналогична схеме распределения активного давления от клина сползания по теории Кулона. При введении допущения о такой аналогии вертикальную эпюру оползневого давления по высоте расчетного сечения склона следует принять треугольной (это подтверждается и тем, что на уровне поверхности скольжения давление является максимальным). Автором проводились вариационные расчеты, которые давали возможность построить вертикальную эпюру оползневого давления. Такие эпюры по форме совпадали с треугольником. Кроме того, величина плеча приложения силы E оп от поверхности скольжения при определении по методам Г.М. Шахунянца и ДИИТа, как правило, получалась близкой к одной трети мощности оползневой толщи. Такое же значение плеча рекомендуют и другие исследователи [ 17, 26, 39]. В связи со сказанным в данной работе принимается допущение о распределении оползневого давления по высоте расчетного сечения склона в виде треугольной эпюры. Также допускается, что реакция противооползневого удерживающего сооружения направлена по горизонтали. В связи с этим далее определяется, как правило, горизонтальная равнодействующая оползневого давления.
Кроме того, зададимся значением коэффициента устойчивости укрепляемого склона K у э , на которое умножается суммарное значение сдвигающих сил при вычислении оползневого давления (далее показано, что умножать на K у э необходимо именно сдвигающие силы, а не результирующее значение оползневого давления E оп ).
В справочниках по основаниям и фундаментам приводятся значения коэффициента устойчивости K у при укреплении склонов с помощью обычных противооползневых мероприятий. При таком укреплении степень неопределенности задачи достаточно высока, поэтому указанные значения K у сравнительно велики. С повышением точности расчетов и с применением более рациональных противооползневых конструкций значение требуемого коэффициента устойчивости должно снижаться.
В одной из своих работ Н.Н. Маслов писал, что возникает вполне оправданное представление о возможности при закреплении действующих оползней ограничиваться лишь весьма небольшим превышением значения K у над единицей. В большинстве случаев при подобных обстоятельствах оказывается достаточным задаваться значениями K у от 1,05 до 1,1. При этом далее слабое торможение может остановить оползень.
При проектировании удерживающих сооружений глубокого заложения тем более не следует задаваться слишком большим коэффициентом устойчивости, поскольку такие конструкции рассчитываются на весь избыток сдвигающих сил.
В связи с изложенным, при расчете противооползневой удерживающей конструкции задаваемый коэффициент устойчивости рекомендуется принимать в пределах [ 6]:
1,01 ≤ K у э ≤ 1,1. ( 3)
Из всех существующих в настоящее время методов расчета автором были рассмотрены лишь те, которые наиболее широко используются для вычисления коэффициента устойчивости склона, и те, которые можно применить для определения оползневого давления. В работе не рассматривались так называемые пространственные методы расчета, в которых вычисления ведутся не для полосы склона шириной 1 м, а для всего объема грунта. По мнению автора, значительное усложнение расчетов в таких методах не оправдывается каким-либо уточнением результатов. Дело в том, что грунтовые условия по ширине склона весьма неоднородны, прочностные характеристики грунтов резко изменяются даже на соседних площадках, следовательно, объединять разнородные условия в один расчет смысла не имеет. Более правильным будет проводить расчет для каждого поперечника в отдельности (и в нем принимать полосу склона шириной 1 м), однако, таких поперечников на склоне выделять как можно больше - для всех мест с изменяющимися физико-механическими и прочностными характеристиками грунтов.
1.2 . Учет действия грунтовых вод
Действие грунтовых вод на состояние оползневого склона проявляется различными путями. Вода оказывает взвешивающее действие на слагающие склон породы, изменяя силы гравитации. Насыщая грунты, вода изменяет их физико-механические характеристики и, в частности, сдвиговые характеристики, уменьшая величину сопротивления сдвигу. Кроме того, грунтовые воды, смачивая возможные поверхности скольжения, в виде смазки уменьшают силы трения. При этом вода, взвешивая грунтовый скелет, снижает за счет порового давления нормальные напряжения σ в плоскости сдвига и может привести к почти полному снятию внутреннего трения в грунте [ 7]. Механизм этого явления ясен из уравнения сдвига
τ = (σ - u ) tg φ + c . ( 4)
Легко видеть, что при достаточном возрастании порового давления u величина σ - u может оказаться равной нулю, и тогда сопротивление грунта сдвигу τ будет определяться только сцеплением. Таким образом, вода снижает несущую способность грунта [ 18].
Важным фактором является также проявление фильтрационного давления грунтовых вод. Как известно, фильтрационное давление создается во всех случаях движения подземных вод. Где есть градиент, где наблюдается уклон поверхности свободного подземного потока или линии пьезометрического уровня для напорных вод, там есть падение напора. Падение напора вызывается преодолением сопротивления течению воды в грунте. Это сопротивление в виде реакции и создает фильтрационное давление. Обычно подземный поток течет в сторону поверхности склона. Понятно, что при этом толща, слагающая склон, испытывает фильтрационное давление, имеющее одинаковое основное направление с оползневым давлением. Следовательно, фильтрационное давление является одним из факторов - побудителей к развитию оползневых явлений.
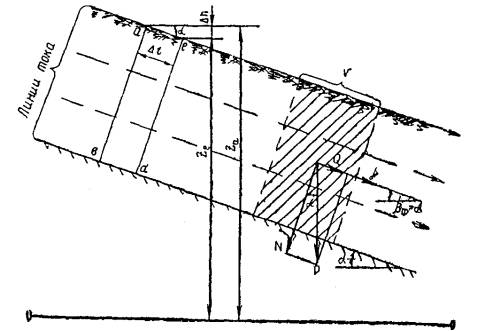
Рис. 1 . Наклонный пласт водонасыщенного грунта
Разберем действие фильтрационного давления для случая наклонного пласта грунта, залегающего на водоупоре, параллельном поверхности (рис. 1). Этот случай благодаря своей простоте позволяет отчетливо представить сущность рассматриваемого вопроса [ 16]. Кроме того, он имеет и практическое значение, так как весьма часто встречается в задачах об устойчивости оползневых склонов и, в виде одного из допущений, может быть использован в большинстве действительных случаев.
Пусть поры грунта полностью насыщены водой и линии тока воды параллельны поверхности откоса. Тогда последняя является, вместе с тем, верхней линией тока, а также и линией депрессии, так как на нее непосредственно действует во всех точках атмосферное давление.
Как известно из гидравлики, линии, перпендикулярные к линии тока, представляют собой эквипотенциальные линии, то есть во всех точках каждой такой линии вода поднялась бы в пьезометрических трубках до одного и того же пьезометрического уровня. Отсюда следует, что вдоль отрезков линий тока, проведенных между двумя эквипотенциальными линиями, будет наблюдаться одинаковая разность пьезометрических уровней, а, следовательно, и одинаковая разность напоров. В данном случае разность напоров Δh между двумя соседними эквипотенциальными линиями, например, ab и ed , будет равна разности отметок точек a и e , т.е. za - ze . Следовательно, Δh = za - ze . Соответствующая длина линии тока будет равна:
Δ l = Δh/ sin α = ( za - ze)/ sin α.
Таким образом, градиент окажется равным:
i = Δh/Δl = ( za - ze) sin α/( za - ze) = sin α. ( 5)
Но поскольку принято α = β ф , то
i = sin β ф . ( 6)
Гидродинамическое (фильтрационное) давление на единицу объема грунта равно градиенту (разности напоров на единицу длины, т.е. объему столба воды), умноженному на удельный вес воды:
j един. = i γω = γωsin β ф . ( 7)
Общее давление на некоторый слой грунта объемом V будет равно:
j = Vj един. = V γωs in β ф = V γω sin α . ( 8)
Это давление направлено вдоль линий тока, параллельно поверхности откоса, и является сдвигающей силой.
Пусть поверхностью скольжения является кровля водоупора. Собственный вес грунта в объеме V с учетом взвешивания будет равен: P в = ( γ - γω ) V . Сдвигающая составляющая этого веса Q также направлена вдоль откоса книзу и равна: Q = P в sin α , а нормальная к поверхности скольжения составляющая N = P в cos α. Таким образом:
Q = ( γ - γω ) V sin α ; N = (γ - γω )V cos α. ( 9)
Общая сдвигающая сила равна Q + j , а удерживающая сила трения T = N tg φ (если в грунте отсутствует сцепление, в противном случае следует добавить силу cL ). Коэффициент устойчивости склона для слоя объемом V будет равен:
![]() . ( 10)
. ( 10)
При отсутствии фильтрационного и взвешивающего давлений этот коэффициент был бы равен:
![]() ( 11)
( 11)
Следовательно, при насыщении откоса водой коэффициент устойчивости снижается в γ / ( γ - γω ) раз, то есть во столько раз, во сколько вес скелета грунта в воздухе больше веса скелета с учетом взвешивания в воде.
Легко видеть, что ту же формулу коэффициента устойчивости можно получить, не рассматривая отдельно фильтрационного давления, а определяя сдвигающую силу исходя из объемного веса грунта γ (то есть веса скелета вместе с водой), а удерживающую силу трения - исходя из веса скелета с учетом взвешивания ( γ - γω ) :
![]() ( 12)
( 12)
Такой способ оценки устойчивости склона обычно называют «методом взвешивания» и нередко применяют при практических расчетах. Физический смысл этого метода заключается в том, что напор грунтовых вод способен оказать на покровную толщу пород взвешивающее противодавление и тем самым снизить действующие в контактной зоне силы сопротивления сдвигу за счет снижения сил трения. Вместе с тем в этих условиях возникает возможность дополнительного водонасыщения грунтов и снижения сопротивляемости их сдвигу. Сдвигающее же усилие в этом случае останется без изменения, так как силы гравитации сохраняются прежней величины (имеется водонасыщение не по всей высоте грунтовой толщи).
Поскольку пьезометрический уровень, соответствующий какой-либо точке поверхности скольжения, находится на отметке пересечения с поверхностью депрессии эквипотенциали, проходящей через эту точку, то нейтральное (поровое) давление в этой точке равно γω h (где h - пьезометрическая высота в данной точке) и направлено по нормали к поверхности скольжения. Следовательно, оно должно быть вычтено из нормального давления, создаваемого весом грунта, находящегося выше поверхности скольжения. Приближенно можно принимать, что пьезометрическая высота h в каждой точке поверхности скольжения равна вертикальному расстоянию между этой точкой и поверхностью депрессии. Это почти точно для пологих откосов (с крутизной меньшей, чем 1:2,5) и идет в запас устойчивости для более крутых откосов. Тогда учет действия воды в порах при расчете устойчивости может выполняться следующим образом. При определении нормального давления по поверхности скольжения от него отнимается величина, равная γω h , а при определении сдвигающих сил учитывается полный объемный вес грунта без взвешивания (т.е. вес скелета плюс вес воды в порах). То есть опять приходим к методу взвешивания.
Итак, учет действия напорных грунтовых вод может производиться двумя способами.
Первый способ учета действия грунтовых вод - метод использования величины гидродинамического давления. Заключается он в следующем:
сдвиговые характеристики грунта в уровне поверхности скольжения принимаются для случая его водонасыщения ( c в , φв);
собственный вес грунта во всех расчетах принимается с учетом взвешивания в воде части оползневого отсека между кривой депрессии и поверхностью скольжения;
к величине сдвигающей силы добавляется величина гидродинамического давления j = V γωsin β ф .
Поскольку, как правило, к оползневому грунту приурочен грунтовый поток, разгружающийся вблизи основания склона, можно с некоторым приближением считать, что в пределах каждого отсека равнодействующая гидродинамического давления параллельна депрессионной кривой, а средний градиент напора в отсеке ii = sin β ф i , где β ф i - угол наклона к горизонту хорды, соединяющей точки пересечения депрессионной кривой с границами отсека. То есть принимаем, что уклон кривой депрессии совпадает с наклоном равнодействующей гидродинамического давления. Положение депрессионной поверхности определяется по материалам инженерно-геологических изысканий и длительных наблюдений с помощью поропьезометров. По результатам экспериментальных данных [ 35] установлено, что направление грунтового потока в сторону напорного откоса приближается (стремится) к линии откоса, поэтому в пределе гидравлический градиент иногда может быть принят равным sin β , где β - угол наклона откоса к горизонту.
При выполнении расчетов устойчивости склонов, как правило, будем принимать, что направление гидродинамической силы параллельно поверхности скольжения в данном отсеке (основанию отсека). В таком случае эту силу можно целиком (без разложения на составляющие) прибавлять к сдвигающей силе. Это, разумеется, не совсем правильно, однако, значительно упрощает расчет и идет в запас прочности. Раскладывать гидродинамическую силу рекомендуется лишь тогда, когда ее наклон будет значительно отличаться от наклона поверхности скольжения (более чем на 10 %). Следует отметить, что при необходимости разложения гидродинамической силы на составляющие (при значительных ее наклонах) его следует выполнять с учетом градиентов потока в соответствующих направлениях, отвечающих гидродинамической сетке фильтрационного потока. При рассмотрении метода Ю.И. Соловьева будет показано, что разложение гидродинамической силы на составляющие значительно усложняет расчет. Этот первый способ учета действия грунтовых вод будем преимущественно применять в таких методах расчета устойчивости склона или величины оползневого давления, в конечных формулах которых нет явно выраженных отдельных величин удерживающей и сдвигающей сил. Однако этот способ приемлем и в любых других случаях.
Второй способ учета действия грунтовых вод - метод взвешивания. Заключается он в следующем:
сдвиговые характеристики грунта в уровне поверхности скольжения принимаются для случая его водонасыщения ( c в , φв);
при определении сил, сдвигающих массив грунта, принимается полный вес отсеков без учета взвешивающего действия грунтовых вод, а при определении сил, удерживающих массив грунта, принимается вес отсеков с учетом взвешивающего действия грунтовых вод в части, находящейся между кривой депрессии и поверхностью скольжения (при этом в вес отсека включается полный объемный вес грунта, находящегося в зоне капиллярного насыщения выше кривой депрессии).
Этот второй способ учета действия грунтовых вод используется для методов расчета, в которых удерживающие и сдвигающие силы оказываются явно выраженными. В целом же оба рассмотренных способа учета действия напорных грунтовых вод равноценны и могут в одинаковой степени применяться в инженерных расчетах.
При отсутствии напорных грунтовых вод и наличии обычного водонасыщения грунтов откоса в расчете коэффициента устойчивости или величины оползневого давления учитываются лишь все физико-механические характеристики пород в замоченном состоянии. Взвешивающее же действие воды или гидродинамическое давление в таком случае не учитывается.
Для возможности оперирования имеющимися в каждом конк ретном случае физико-механическими характеристиками грунтов вспомним различные способы определения объемного веса грунта при его водонасыщении или увлажнении. Объемный вес γ грунта в естественном состоянии с влажностью W равен:
γ = γ r (1 + 0,01 W )/(1 + e ). ( 13)
Объемный вес γбр грунта, полностью насыщенного водой (вес грунта брутто), определяется по формуле
γбр = ( γr + γωe )/(1 + e ) = γ в + γω = γ ск + n γω . ( 14)
Объемный вес γв грунта, взвешенного в воде (взвешенный объемный вес грунта), определяется по следующим формулам:
для водопроницаемых грунтов (пески, гравий, щебень, трещиноватые полускальные породы и т.д.)
γв = ( γr - γω )/(1 + e ); ( 15)
для непроницаемых и слабопроницаемых грунтов (глинистых, монолитных скалистых, супесей, плотных песков и т.д.)
γв = γ - γω = γск - (1 - n ) γω . ( 16)
Все физико-механические характеристики грунтов, в том числе и характеристики сопротивляемости грунтов сдвигу ci и φi , различны в основаниях отсеков, находящихся ниже уровня грунтовых вод и выше их. Поэтому целесообразно границы отсеков располагать так, чтобы эти границы совпадали с переходом от части основания блока, находящейся выше грунтовых вод, к части, находящейся под ними.
В заключение данного параграфа необходимо оговориться, что приведенные здесь способы учета действия грунтовых вод являются далеко не единственными. Например, И.В. Федоров [ 26] предложил способ расчета устойчивости откосов с учетом фильтрационных сил, удовлетворяющий всем условиям статики, графоаналитическим методом. Некоторые элементы данного способа будут нами использованы при рассмотрении соответствующих методов оценки устойчивости склонов и откосов. Этим же автором [ 27] проанализированы выведенные различными исследователями уравнения движения воды в пористых средах и предложена для практического использования методика расчета эффективного давления по подошве элемента при учете фильтрационных сил.
Р.Р. Чугаевым выведены дифференциальные уравнения движения жидкости в грунте и получены выражения для учета фильтрационных сил [ 32, 33, 35]. При произвольной поверхности скольжения (образованной системой плоскостей) фильтрационные силы можно учитывать с использованием контурного способа Иванова, для которого достаточно располагать только данными о распределении напоров на границах блока. Этим вопросом занимались и многие другие советские и зарубежные ученые (Н.П. Пузыревский, Б.И. Покровский, Д.В. Тейлор, Е.Д. Кадомский, И. Оде, Н.А. Цытович, Н.С. Моргунов, К.И. Фоменко, Ю.А. Соболевский, М.Е. Харр и др.). В некоторых случаях получены решения, отличающиеся большой точностью. Однако, из-за ограниченности места, мы не будем здесь подробно рассматривать все эти решения. Как показал И.В. Федоров [ 26], учет фильтрационных сил по упрощенной формуле дает незначительные расхождения (до 1,5 %) по сравнению с точными решениями. Этот способ учета особенно применим в практике, так как не требует построения фильтрационной сетки. Для учета фильтрационных сил в данном случае требуется построение лишь кривой депрессии и определение участка высачивания.
Следует заметить, что оценка коэффициента устойчивости с учетом фильтрационных сил по упрощенной формуле будет давать приемлемые результаты только в тех случаях, когда эквипотенциальные линии несущественно отличаются от вертикальных линий.
В связи с вышеизложенным для практического проектирования удерживающих конструкций мы будем применять лишь приведенные в настоящем параграфе два способа учета действия напорных грунтовых вод - метод использования величины гидродинамического давления и метод взвешивания.
Применение более сложных методов учета гидродинамического давления оправдывается в тех случаях, когда имеются значительные напоры грунтовых вод или когда склон омывается акваториями, уровень воды в которых может резко изменяться, и т.д.
1.3 . Учет сейсмических воздействий
Рассмотрим теперь особенности расчета устойчивости склонов или откосов в сейсмических районах [ 16, 20, 23, 39]. Поскольку методика расчета в данной работе будет приводиться в основном применительно к условиям оползневых склонов Южного берега Крыма, Кавказа и Закарпатья, в большинстве своем находящихся в сейсмических районах, действие сейсмики будем учитывать во всех выводимых формулах.
Сила землетрясения оценивается по двенадцатибалльной шкале. Весь Советский Союз районирован по сейсмичности. Для каждого района указывается максимальная балльность, которой может достигнуть землетрясение в этом районе. Расчеты откосов и склонов в районах, для которых сила землетрясения оценивается в 7 баллов и выше, производятся с учетом сейсмичности. Однако на отдельных участках одного и того же по балльности района фактическая сила землетрясений может отличаться от средней в зависимости от геологических условий. Неблагоприятными в сейсмическом отношении являются: насыщенные водой гравийные, песчаные и лессовидные грунты; мягкопластичные и текучие глинистые грунты; участки местности с сильно расчлененным рельефом - обрывистые берега, овраги, ущелья; выветрелые и сильно нарушенные породы; участки с близким расположением линий тектонических разрывов. Менее опасны в сейсмическом отношении невыветрелые скальные грунты, а также плотные и маловлажные крупнообломочные грунты.
При проектировании укрепления оползневых склонов или строительства сооружений на них следует учитывать их геологическое строение. В неблагоприятных геологических условиях, указанных выше, средняя сейсмическая балльность района должна повышаться на один балл; при благоприятных условиях - понижаться на один балл.
Учет сейсмического воздействия при расчете противооползневых удерживающих конструкций осуществляется добавлением к расчетным усилиям так называемой сейсмической силы.
Сейсмическая сила Q с приближенно определяется как доля от веса массы грунта, которая претерпевает сейсмическое воздействие:
Q с = μ P , ( 17)
где μ - коэффициент динамической сейсмичности, значения которого рекомендуется при расчете естественных склонов принимать по табл. 1. При расчете искусственных откосов (насыпи дорог, плотины т.д.) значения коэффициента из табл. 1 следует (приближенно) увеличивать в 1,5 раза.
Таблица 1
Коэффициент динамической сейсмичности μ
|
Сейсмическая балльность района |
1 - 6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
μ |
0,00 |
0,025 |
0,050 |
0,10 |
0,25 |
0,50 |
> 0,75 |
Направление силы Q с рекомендуется считать наиболее неблагоприятным. В связи с этим будем принимать, что силы сейсма в каждом отсеке оползневого блока направлены параллельно основанию отсека, то есть совпадают с направлением сдвигающей силы в этом отсеке. Тогда при разбивке оползневого блока на отсеки сейсмические силы будем учитывать в отдельности при рассмотрении каждого отсека (складывать их со сдвигающими силами). Это, конечно, принципиально неточно, ибо направление сейсмического воздействия должно быть, естественно, единым по длине всего оползневого блока (соответствующим направлению ускорения сейсмической волны). Однако допущение о существовании в каждом отсеке своего направления сейсмической силы значительно упрощает дальнейший расчет и идет в запас прочности.
При сплошном водонасыщении оползневого массива сейсмические силы следует учитывать не только от веса грунта, но аналогичным образом и от веса воды.
Приведенный способ учета сейсмической силы, несомненно, является упрощенным. Однако его простота при применении в инженерных расчетах оправдывает имеющуюся неточность, которая может быть ликвидирована с помощью длительных экспериментальных исследований.
Р.Р. Чугаев [ 34] предложил для учета сейсмического воздействия рассчитываемый оползневой блок целиком поворачивать на угол отклонения результирующей объемной силы (равной равнодействующей вертикальной силы и горизонтальной силы сейсмического воздействия) от вертикали. При этом результирующая объемная сила становится вертикальной. Затем расчет выполняется в обычном порядке при вертикально действующих объемных силах, но для нового положения отсека, при котором на угол отклонения повернуты все элементы блока - верхний и нижний контуры, границы слоев, депрессионная линия, горизонт воды и т.д. Мы при рассмотрении расчетных методов этот способ учета сейсмической силы использовать не будем ввиду его сложности.
II . МЕТОДЫ РАСЧЕТА
2.1 . Метод круглоцилиндрической поверхности скольжения
Способ круглоцилиндрической поверхности широко описан в технической литературе [ 8, 15, 17, 19, 25, 26, 28, 29, 30, 31, 34, 39], однако, не всегда одинаково трактуется у разных авторов.
Этот метод весьма распространен в строительной практике и применяется с помощью самых различных приемов. Поэтому существует большое количество названий рассматриваемого метода и его разновидностей: шведский метод отсеков, метод В. Феллениуса, шведский метод круглоцилиндрических поверхностей скольжения, метод Терцаги, метод Терцаги-Крея, метод Петтерсона, метод вертикальных элементов, метод Иванова-Тейлора, метод Свена Гультена, метод весового давления и т.д.
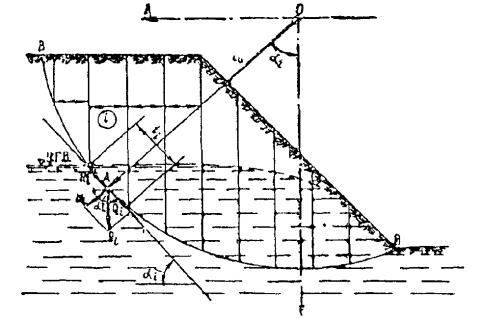
Рис. 2 . Метод круглоцилиндрической поверхности скольжения
Метод круглоцилиндрической поверхности скольжения целесообразно применять, когда откос сложен однородными грунтами. Метод предполагает, что сползание грунта может произойти лишь в результате вращения оползающего массива вокруг центра О (рис. 2). Следовательно, поверхность скольжения ВВ в данном случае будет представлена дугой некоторого круга с радиусом r , очерченного из центра О . Оползающий массив рассматривается при этом как некоторый твердый блок, всеми своими точками участвующий в одном общем движении.
Степень устойчивости откоса оценивается различными методами («метод площадей», «метод круга трения» и т.д.). Принципиально наиболее простым из них и одновременно наиболее распространенным в нашей стране является так называемый метод моментов, сущность которого заключается в следующем.
Оползающий массив находится под воздействием двух моментов: момента M вр , вращающего массив, и момента M уд , удерживающего массив. Коэффициент устойчивости склона K у определяется отношением этих моментов, т.е.
K у = M уд / M вр . ( 18)
Грунтовые воды оказывают взвешивающее влияние на породы и фильтрационное (гидродинамическое) давление на весь массив, как было описано выше. Вращающий момент определяется умножением сдвигающих сил на плечо до центра вращения О, а удерживающий момент - умножением сил сопротивления сдвигу на аналогичное плечо. При этом, так как угол наклона касательной к поверхности скольжения и веса отдельных частей массива не постоянны, приходится расчленять воображаемый оползневой массив (сползающий блок) на n расчетных отсеков, для каждого из которых определяют силы сопротивления сдвигу и сдвигающие силы. Тогда коэффициент запаса устойчивости склона находится как отношение сумм тех и других моментов:
K у = Σ M уд /Σ M вр . ( 19)
Подробный вывод окончательных формул для определения коэффициента устойчивости методом цилиндрических поверхностей приведен у многих авторов. Поэтому мы их здесь дадим без выводов.
При отсутствии грунтовых вод
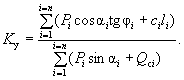 ( 20 -а)
( 20 -а)
При простом затоплении откоса
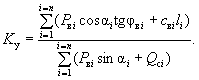 ( 20-б)
( 20-б)
При воздействии на откос фильтрационного потока:
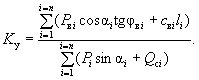 ( 20-в)
( 20-в)
Кроме участвующих в написанных выше формулах сил, в грунтовом массиве имеются еще неизвестные по величине давления грунта на вертикальные боковые грани отсеков. Последние силы являются внутренними по отношению ко всему сползающему массиву и внешними по отношению к отдельным выделенным элементам. Так как независимо от величины и направления боковых давлений сумма всех вертикальных сил должна равняться общему весу сползающего клина, то в методах круглоцилиндрических поверхностей скольжения принимается, что силы бокового давления, действующие на вертикальные грани отдельных элементов грунта, можно не учитывать при определении условий равновесия всего сползающего массива.
Из других способов, использующих круглоцилиндрическую поверхность скольжения, следует упомянуть метод круга трения (приемы Гультина и Петерсона, Казагранде, Крея, Тейлора, Гольдштейна, Федорова и др.), метод многоугольника сил Фрелиха, метод Како, метод Чугаева-Вяземского, метод Бишопа и пр. Все они являются сравнительно эффективными для оценки степени устойчивости склонов, но трудно применимы для определения величины оползневого давления. То же следует сказать о методах расчета устойчивости откоса по кривой скольжения, имеющей форму логарифмической спирали (например, метод Рендулика).
На практике рассматриваемый метод часто осложняется неопределенностью в положении центра вращения О . Его координаты, а также радиус r определяются так, чтобы отразить в расчете наиболее невыгодное положение принимаемой поверхности скольжения, при котором значение коэффициента устойчивости K у получается минимальным из возможных для данного склона (откоса). Очень часто положение центра О устанавливают подбором путем проведения нескольких расчетов для отыскания наиболее опасного для данного случая положения поверхности скольжения. Такой ход расчета связан со значительной трудоемкостью.
Имеются и другие причины, по которым метод круглоцилиндрической поверхности скольжения сложно использовать при проектировании противооползневых удерживающих конструкций глубокого заложения. Например, это связано с тем, что оползневое проявление чаще всего развивается в тех естественных склонах, толща которых сложена пластами различных пород (нередко со слабыми прослойками). Для таких же случаев неоднородных грунтов расчет методом круглоцилиндрической поверхности скольжения не вполне пригоден.
2.2 . Метод Ю.И. Соловьева
В 1962 г. Ю.И. Соловьев предложил при расчете устойчивости откосов, в таком же гипотетическом грунте, какой принимали Герсеванов и Терцаги, воспользоваться принципом возможных перемещений [ 2, 8, 22]. Поверхность скольжения при этом должна рассматриваться как поверхность контакта между клином обрушения и подстилающим грунтом, по которой на клин действуют односторонние силы связи и внешние касательные силы сцепления и трения (рис. 3). Коэффициент устойчивости склона по Ю.И. Соловьеву представляет собой отношение работ удерживающих и сдвигающих сил на перемещении, которое для всех отсеков имеет одинаковую горизонтальную составляющую u о . Это означает, что при скольжении всего клина, он сохраняет сплошность и в нем отсутствуют разрывы, но могут происходить касательные смещения по вертикальным плоскостям, по которым, в соответствии с принятым предположением о свойствах гипотетического грунта, сопротивление сдвигу отсутствует. Возможные перемещения S , которые допускаются связями системы, будут происходить вдоль поверхности скольжения и для любого отсека будут равны:
S = u о /cos αi .
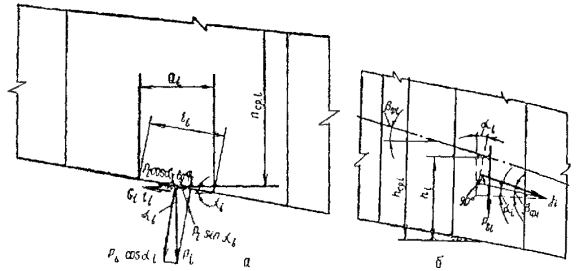
Рис. 3 . Метод Ю.И. Соловьева:
а - основная схема; б - учет фильтрационного давления
Как известно, принцип возможных перемещений гласит: необходимое и достаточное условие равновесия состоит в том, что сумма работ всех сил на виртуальных перемещениях системы должна быть равна нулю.
Напишем выражения работ сдвигающих и удерживающих сил на возможных (виртуальных) перемещениях:
работа сдвигающих сил
A сдв = ∫ SdQ = ∫( u о / cos α ) × P sin αdx ;
A сдв = u о ∫ P tg αdx ; ( 21)
работа удерживающих сил
A уд = -∫ SdR = -∫( u о / cos α )( P cos α tg φdx + c ( dx / cos α );
A уд = - u о ∫ ( P tg φ + c / cos 2 α ) dx . ( 22)
Поскольку в данном случае заранее известно, что система сдвигающих и удерживающих сил в общем случае неуравновешена, то для того, чтобы сумма работ этих сил на виртуальных перемещениях была равна нулю, необходимо сдвигающие силы увеличить в K у раз, т.е. положить
K у A сдв + A уд = 0. ( 23)
Безразмерный числовой множитель K у в этом выражении и есть коэффициент запаса устойчивости. Принимая во внимание полученные выражения для работ удерживающих и сдвигающих сил, найдем
K у = - A уд / A сдв = 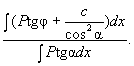 ( 24)
( 24)
Если применяется метод численного интегрирования с разбивкой призмы обрушения (оползневого блока) на конечное число элементов (отсеков), то работа удерживающих сил на возможных перемещениях для одного отсека будет равна:
A уд i = ( u о / cos αi ) ( Pi cos αitg φi + cili ) = u о ( Pi tg φi + cili / cos αi ), ( 25)
а работа сдвигающих сил для одного отсека будет равна:
A сдв i = ( u о / cos αi ) ( Pi sin αi + Q с i ) = u о ( Pi tg α i + Q с i / cos αi ). ( 26)
Тогда коэффициент устойчивости склона по данному методу определится как отношение суммы работ удерживающих сил к сумме работ сдвигающих сил на возможных перемещениях:
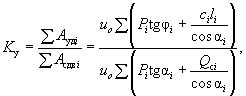 ( 27)
( 27)
и при отсутствии грунтовых вод выразится формулой
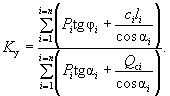 ( 28-а)
( 28-а)
При обычном затоплении склона грунтовыми водами коэффициент устойчивости будет иметь следующее значение:
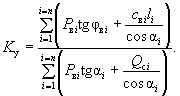 ( 28-б)
( 28-б)
Выведем эту же формулу для случая, когда на склоне проявляется гидродинамическое давление. Причем для примера примем, что наклон фильтрационной силы значительно отличается от наклона поверхности скольжения, в связи с чем требуется раздельно учитывать обе составляющие этой силы.
Вес грунта в каждом выделенном отсеке будем принимать с учетом взвешивания в воде (за минусом веса воды в данном отсеке между поверхностью скольжения и депрессионной кривой), но прибавлять к его нормальной составляющей величину проекции гидродинамического давления на нормаль к поверхности скольжения. Кроме того, к сдвигающим силам добавим проекцию гидродинамического давления на направление поверхности скольжения (см. рис. 3, б). Вес грунта с учетом взвешивания
P в i = γ i h ср. i ai - γωhiai ;
фильтрационное давление
ji = γ ω ωiii = γωhiaiii .
Его проекция на нормаль к поверхности скольжения:
γωhiaiiisin ( β ф i - αi ).
Его проекция на поверхность скольжения:
γωhiaiiicos ( β ф i - αi ).
С учетом этих сил выражения работ для каждого отсека будут:
A уд i
= ( u о / cos αi ) [ P в i cos αitg φ в i
+ γωhiaiiisin ( β ф i - αi ) tg φ в i
+ c в i li ] = u о {[ P в i + γωhiaiii ![]() ] tg φ в i + c в i li / cos αi } ;
] tg φ в i + c в i li / cos αi } ;
A сдв i = ( u о / cos αi ) [ P в i sin αi + γωhiaiiicos ( β ф i - αi ) + Qci ] = u о [ P в i sin αi / cos αi + γωhiaiii ( cos β ф i cos αi + sin β ф i sin αi )/ cos αi + Q с i / cos αi ] = u о [ P в i + γωhiaiiisin β ф i ] tg αi + u о ( γωhiaiii cos β ф i + Q с i / cos αi ) .
Тогда:
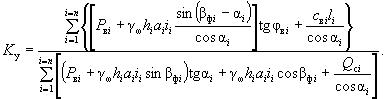 ( 28-в)
( 28-в)
Как видим, выражение для коэффициента устойчивости при учете гидродинамического давления получается сравнительно сложным. Поэтому, где это возможно, проще учитывать гидродинамическое давление, принимая направление его действия параллельным поверхности скольжения (без разложения на составляющие).
Необходимо также помнить, что, как указывалось выше, при разложении фильтрационных сил на направления вертикали и касательной к поверхности скольжения следует учитывать изменение градиента в различных направлениях. Это еще более усложнит расчет.
В 1969 г. М.Н. Гольдштейн [ 8] показал, что хотя по поверхности скольжения действуют силы трения, т.е. силы, не имеющие потенциала, тем не менее и в этом случае принцип возможных перемещений применим к рассматриваемой задаче. Действительно, в соответствии с формулировкой принципа возможных перемещений, данной Фурье для необратимых перемещений и пригодной также для сил, не имеющих потенциала, можно утверждать, что в состоянии предельного равновесия в равную нулю сумму работ на возможных перемещениях всех сил, действующих на систему, должны быть включены и силы трения, заменяющие действие внутренних связей, существовавших в системе до образования поверхности раздела в виде поверхности скольжения. Эти силы, естественно, должны быть полностью мобилизованы. Важное условие применимости к данной задаче принципа возможных перемещений заключается в том, что при рассмотрении всего клина обрушения не требовалось учитывать работу внутренних сил на относительных перемещениях отдельных его элементов. Но в случае гипотетического грунта Герсеванова и при условии, что отсеки являются жесткими, а их виртуальные перемещения не нарушают имеющихся кинематических связей, указанное условие выполняется. При этом очевидно, что либо поверхность скольжения должна быть круглоцилиндрической, либо пяты отсеков должны иметь форму, позволяющую им скользить по поверхности сдвига, не наклоняясь и не деформируясь (например, в виде дуг, соприкасающихся с поверхностью сдвига в одной точке).
Иногда проектировщики этим методом определяют оползневое давление, представляя его как разность между знаменателем и числителем в написанных формулах коэффициента устойчивости. Однако такое определение оползневого давления нельзя считать правильным, поскольку числитель и знаменатель выражения коэффициента устойчивости в данном случае есть не силы, а работы.
2.3 . Метод F р
Метод F р (приближенный метод равнопрочного откоса или метод Н.Н. Маслова) более применим для проектирования искусственных откосов, а не для оценки степени устойчивости естественных склонов [ 13, 15]. Однако мы рассмотрим этот метод, поскольку разработанные в нем оригинальные приемы могут быть использованы при решении различных инженерных задач.
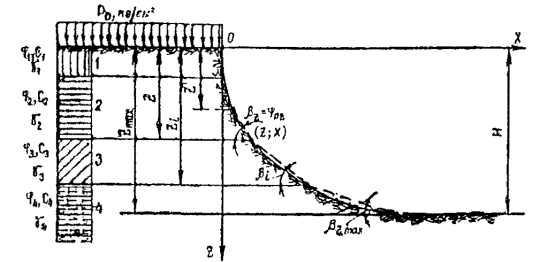
Рис. 4 . Метод F р
Метод F р основывается на положении, что степень устойчивости откоса или склона определяется минимальной величиной коэффициента K у из всех его значений по высоте откоса. Вместе с тем для каждого из горизонтов (рис. 4) величина K у определяется из условия
K у = tg ψ р /tg β. ( 29)
где β - угол наклона к горизонту откоса в рассматриваемой точке;
ψ р - угол сопротивления сдвигу на этом горизонте (или угол сдвига).
Угол сопротивления сдвигу ψ р для сыпучих (зернистых) грунтов, лишенных сцепления ( c = 0), равен углу внутреннего трения, т.е. ψ р = φ . Тогда написанная выше формула приобретает для таких грунтов следующий вид:
K у = tg φ/tg β . ( 30)
Так как tg ψ р = F р = tg φ + c / σn , то для рассматриваемого случая
tg ψ р = F р z = tg φ + c / γz . ( 31)
При наличии за бровкой откоса равномерно распределенной нагрузки p о последнее выражение приобретает вид:
F р z = tg φ + c /( γz + p о ). ( 32)
Очевидно, что φ и c должны подставляться в приведенные выше формулы применительно к своим значениям для рассматриваемого пласта и степени консолидации грунта. Объемный вес γ определяется здесь своим средним значением для всей толщи, перекрывающей данный горизонт, с учетом в необходимых случаях взвешивания грунта водой.
Равнопрочный откос в состоянии своего предельного равновесия по методу F р определяется условием, что для каждой точки откоса с глубиной z от свободной поверхности удовлетворяется условие:
βz = ψ р z . ( 33)
Иными словами, на каждом горизонте z угол наклона откоса к горизонту βz численно равен углу сопротивления сдвигу ψ р z , характерному для данного горизонта.
Профиль равнопрочного откоса, как правило, имеет криволинейное очертание, более крутое в верхней и более пологое в нижней части.
Построение такого откоса, а равным образом и откоса с наперед заданным значением коэффициента K у по выражению ( 29) может быть осуществлено графически и аналитически. В последнем случае используется следующее выражение (проф. Н.Н. Маслов):
x = (1/ γt g 2 φ ){ tg φ γz + c ln ( tg φ p о + c ) - c ln [ t g φ ( γz + p о ) + c ]} , ( 34-а)
где x - абсцисса точки на поверхности откоса, отвечающая глубине z расчетного горизонта от поверхности толщи.
При отсутствии за бровкой откоса нагрузки ( p о = 0) предыдущее выражение упрощается:
x = (1/ γt g 2 φ )[ tg φ × γz + c ln c - c ln ( t g φ × γz + c )]. ( 34-б)
Аналитический метод построения равнопрочного откоса является более точным, чем графический. Однако при наличии в толще откоса нескольких пластов с различными механическими характеристиками этот метод становится излишне громоздким и явно уступает графическому приему.
Сущность графического приема по методу F р базируется на использовании выражения, вытекающего из ранее написанной зависимости ( 29):
tg β = (1/ K у ) tg ψ р . ( 35)
Откос разделяется по высоте на ряд расчетных слоев с подошвой на глубинах z 1 , z 2 , …, zn от поверхности толщи. При уменьшении мощности этих слоев точность построения повышается. При наличии в толще откоса пластов различных пород соответствующие расчетным слоям горизонты должны совпадать с контактами этих пластов. Далее для каждого из этих горизонтов с глубиной zi находят значение угла сопротивления сдвигу ψ р z по выражению ψ р z = arctg Fpz через значение коэффициента сопротивления сдвигу
Fpz = tg φi + ci /( γz + p о ).
После этого определяют соответствующие найденным значениям углов сопротивления сдвигу ψ р z величины углов откоса β , задавшись тем или иным коэффициентом запаса устойчивости K у . В равновесном положении K у = 1. В этом случае имеет место соблюдение равенства βz = ψ р z .
Построение откоса начинается с нижней его точки для zmax = H . Здесь откладывается отвечающий данному горизонту угол β zmax . Продолжаем определяющую его линию до пересечения со следующим горизонтом на глубине zi . В точке пересечения откладываем снова угол βz , соответствующий этому горизонту. Находим новое пересечение определяющей его линии с очередным менее глубоко расположенным горизонтом и т.д., вплоть до выхода откоса на поверхность. Полученные указанным выше построением точки пересечения расчетных горизонтов с линиями, определяющими углы откосов βi , соединяем плавной кривой. На этом построение равнопрочного откоса графическим методом заканчивается.
Отметим, что при отсутствии на поверхности толщи за бровкой откоса нагрузки, т.е. при p о = 0, и при наличии в грунте даже самого незначительного сцепления c угол откоса β на поверхности толщи при z = 0 становится равным 90°. Это положение вытекает из выражения
ψ р = arctg F р = arctg ( tg φ + c / γz ) при z = 0 c ≠ 0 = arctg µ = 90°. ( 36)
Рассмотренный метод дает, как мы видели, возможность построить равнопрочный откос, т.е. откос, на всем протяжении которого по высоте коэффициент устойчивости одинаков. Однако метод F р не может быть применен для расчета величины оползневого давления.
2.4 . Метод Р.Р. Чугаева
Р.Р. Чугаев [ 34] этот метод называет еще методом плоских поверхностей сдвига, ибо он применим лишь в случаях, когда поверхность скольжения является плоской или состоит из отдельных прямолинейных участков.
В данном методе обозначаются: φд, c д - действительные величины угла внутреннего трения и сцепления, т.е. величины, которыми характеризуется рассматриваемый грунт; φ к , c к - критические значения угла внутреннего трения и сцепления, т.е. те значения, которые надо придать грунту, чтобы рассматриваемый оползневой блок пришел в состояние предельного равновесия; τк, σк - критические величины касательного и нормального напряжений, т.е. величины, которые появляются в момент предельного равновесия.
Заменив действительный земляной откос моделью отвердевшего оползневого блока, можем составить для него, в результате расчета в соответствии с формулой τк = σк tg φк + c к , соответствующее уравнение предельного равновесия в виде
c к = f 1 ( tg φк) или c к = f 2 (φк). ( 37)
Графически это уравнение представлено на рис. 5 кривой ab , которая называется кривой связи. Каждая точка этой кривой дает нам пару значений c к и φ к , при которых рассматриваемый блок находится в состоянии предельного равновесия. Через φ к о обозначено то значение φ к , при котором c к = 0; через c к о обозначено то значение c к , при котором φ к = 0. Непосредственные подсчеты показывают, что кривая связи ab , как правило, близка к прямой.
Если значения φ д и c д дают точку m , лежащую ниже кривой связи ab , то рассматриваемый оползневой блок является неустойчивым, так как слагающий его грунт имеет характеристики сдви га менее критических значений. Если же величины φ д и c д дают точку n , лежащую выше кривой связи ab , то рассматриваемый блок находится в устойчивом равновесии; при этом чем дальше точка n располагается от кривой ab , тем больший запас устойчивости имеет данный массив грунта.
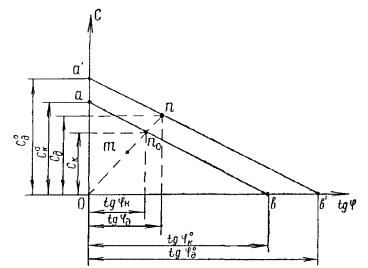
Рис. 5 . Кривые связи
Чтобы исправить погрешности принятой модели отвердевшего тела и приближенного способа расчета этой модели, а также погрешности в определении принятых для расчета величин φ д и c д , полученную расчетом прямую связи ab переносим параллельно самой себе на некоторое расстояние в положение a ' b ' , т.е. в положение линии, проведенной через заданную точку n параллельно теоретической кривой связи ab . Именно эта прямая a ' b ' есть прямая связи, проведенная с надлежащим запасом. Искомый коэффициент запаса K у должен в аналитической форме отражать перенос прямой ab в положение a ' b ' . Поэтому в данном методе принимается, что для величины K у можно написать, например, выражения (см. рис. 5):
K у = ( tg φ д )/ tg φ к = c д / c к ( 38-а)
или
K у = φ д / φ к = c д / c к . ( 38-б)
Далее расчет устойчивости склона, основанный на использова нии модели отвердевшего блока обрушения, сводится к расчету ряда произвольно заданных отсеков обрушения. При этом в процессе рассмотрения того или иного произвольно заданного блока в общем случае последовательно решаются две независимые друг от друга задачи:
1 ) рассчитывается так называемая предельная схема данного оползневого блока, причем, исходя из уравнения предельного равновесия, относящегося к этой схеме, устанавливаются критические значения угла внутреннего трения и силы сцепления грунта;
2 ) зная эти критические величины, устанавливается на их основе численное значение коэффициента запаса устойчивости данного оползневого блока.
В выводах Р.Р. Чугаева [ 34] уравнение предельного равновесия для оползневого блока, ограниченного снизу произвольной поверхностью сдвига (образованной несколькими плоскостями), дается для нескольких способов расчета:
а) способа горизонтальных сил взаимодействия, основанного на допущении, что η = 0, где η - угол наклона к горизонту силы E взаимодействия, передающейся от одного вертикального отсека к соседнему через боковую вертикальную поверхность;
б) способ предельно наклонных сил взаимодействия, основанный на допущении, что η = Ψ рк , где Ψ рк - критический угол сдвига (равный в случае сыпучего грунта величине φ к );
в) способ наклонных сил взаимодействия, основанный на допущении, что η = 0,5 Ψ рк .
Однако при выборе наиболее рациональных способов расчета Р.Р. Чугаев доказывает, что в случае обычных земляных откосов, когда β ≤ 50 - 60°, следует пользоваться способом наклонных сил, основанном на допущении, что η = 0,5 Ψ рк . Поэтому мы будем здесь рассматривать только этот способ.
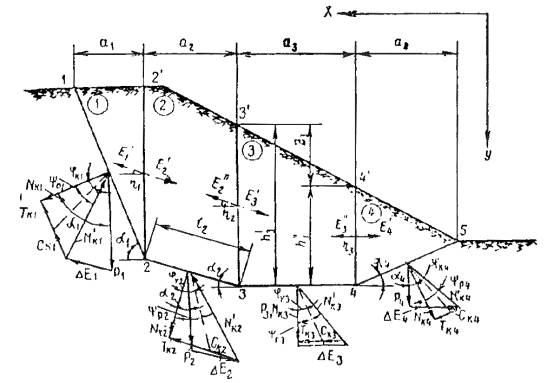
Рис. 6 . Метод Р.Р. Чугаева
Представим на рис. 6 оползневой откос, ограниченный снизу заданной поверхностью скольжения 1 - 2 - 3 - 4 - 5, которая образована несколькими плоскостями. Разобьем оползневой блок вертикалями на соответствующее число отдельных отсеков (принимаемых далее твердыми телами). Считаем, что силы E взаимодействия между отдельными отсеками, передающиеся через их вертикальные границы, наклонены к горизонту под углами ηi = 0,5 Ψ р i . Далее строим на рис. 6 соответствующие многоугольники сил, в которых N 'к i - реакция основания в момент предельного равновесия, действующая на подошву i -го отсека и подсчитанная с учетом сил N к i , T к i , c к i . Затем составляем уравнения равновесия, проектируя все силы на горизонтальную ось. При этом считаем, что предельное равновесие имеет место не только в районе поверхности сдвига, но и в районе всех вертикальных границ, которыми мы разбиваем оползневой блок на отдельные отсеки. Причем в процессе данных выводов эффект действия сил сцепления заменяется эффектом, который получается в результате обжатия грунта в отдельном отсеке всесторонним нормальным давлением интенсивностью
q = c к /tg φ к . ( 39)
В результате определенных преобразований (подробный вывод можно найти в книге Р.Р. Чугаева [ 34]) получается уравнение предельного равновесия для однородного связного грунта:
![]() ( 40)
( 40)
где
![]() ( 41)
( 41)
zi - разность отметок поверхности земли с левой и с правой сторон отсека (например, точек 3' и 4' на рис. 6; если отметка точки 4' больше отметки точки 3', то zi приобретает отрицательное значение).
Пользуясь уравнением предельного равновесия ( 40), можно легко построить для данного оползневого блока кривую связи c к = f ( φк ). Для этого, зная размеры блока, следует задаваться величиной φк и затем по формуле ( 40) вычислять соответствующие значения c к . То есть уравнение предельного равновесия решается только подбором.
При рассмотрении равновесия отдельного отсека, кроме того, отыскивается вектор геометрической суммы сил Ei ' и Ei " , действующих на данный отсек слева и справа:
ΔEi = Ei' + Ei" , ( 42 )
а также величина горизонтальной проекции ΔExi этого вектора (для однородного связного сухого грунта):
ΔExi = ± PiAoi cos ( φ к /2) - { Aoi cos ( ω к /2)[ zi c tg ( αi ![]() φ к )
φ к ) ![]() a i ] + ( hi " - h ' i )} c к / tg φ к , ( 43)
a i ] + ( hi " - h ' i )} c к / tg φ к , ( 43)
где zi , h ' i , h " i - геометрические размеры, показанные на рис. 6 для третьего отсека. Причем zi не есть разница между h ' i и h " i , а превышение левой верхней точки отсека над правой (при наклонной подошве отсека это не одно и то же).
Величины zi и ( h " i - h ' i ) могут быть как положительными, так и отрицательными; угол α i всегда должен считаться положительным.
Применяя принципы теории предельного равновесия к запредельному состоянию, можем допустить, что горизонтальная составляющая суммарного оползневого давления в конце n -го отсека будет равна:
E оп = ![]() ( 44)
( 44)
или
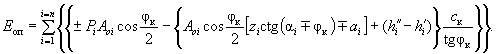 ( 45)
( 45)
В написанных зависимостях верхний знак отвечает нисходящей (падающей), а нижний - восходящей (поднимающейся) поверхности сдвига. В случае отсека, имеющего горизонтальную подошву, можно пользоваться или верхними знаками или нижними - результат расчета от этого не должен изменяться.
При определении оползневого давления в запредельном состоянии склона сдвиговые характеристики грунта c к и φ к , с определенным допущением, можно принимать для состояния предельного равновесия. При этом, если в склоне уже появлялись оползневые подвижки, сдвиговые характеристики можно определять непосредственно для грунта, находящегося в уровне поверхности скольжения. В таком случае рекомендуется применять методы натурного определения c и φ непосредственно в шурфе.
Далее преобразовываем приведенные выше зависимости для случая неоднородного грунта, а также учета фильтрационных и сейсмических сил.
Следует различать неоднородность грунта в отношении его объемного веса и в отношении его прочностных характеристик φ д и c д .
Учет неоднородности в отношении γ осуществляется относительно просто. В уравнение предельного равновесия ( 40) и формулу оползневого давления ( 45) входят величины собственного веса отдельных отсеков, на которые разбивается данный оползневой блок. Очевидно, что в случае, когда тот или другой рассматриваемый отсек состоит из частей, образованных грунтом разного объемного веса, величина которого нам задана, то возможно подсчитать собственные веса этих отдельных частей, а затем их сложить. Или же для всего отсека принимать средневзвешенное значение объемного веса грунта.
Учет неоднородности грунта в отношении φд и c д осуществляется в рассматриваемом методе расчета следующим образом.
В процессе всех вычислений принимаем в расчет только те величины φд и c д , которые относятся к грунту, расположенному непосредственно вблизи поверхности скольжения. Значениями φд и c д , относящимися к грунту, расположенному внутри оползневого блока (вдали от поверхности скольжения), не интересуемся. Поэтому с целью облегчить расчет, разбиваем оползневой блок на отсеки таким образом, чтобы в пределах подошвы каждого отдельного отсека грунт был бы однородным в отношении φд и c д . Кроме того, чтобы не усложнять расчет, будем принимать угол сдвига Ψ рк не для грунта, расположенного в районе граничной вертикали, расчленяющей оползневой блок на отсеки (как это требуется), а для грунта в районе рассматриваемого участка поверхности скольжения (часто эти углы по величине совпадают).
Следующее допущение связано с вопросом о доведении данного действительного оползневого блока до его предельной схемы.
Чтобы получить предельную схему, представим себе, что прочностные характеристики грунта φд и c д постепенно уменьшаются до тех пор, пока рассматриваемый оползневой блок не придет в состояние предельного равновесия. При этом считаем, что в процессе такого воображаемого уменьшения прочностных характеристик величина отношения между отдельными характеристиками (между отдельными значениями φд или между отдельными значениями c д ) все время сохраняется постоянной. Теперь выберем произвольно какой-то участок поверхности скольжения и назовем его основным. Он будет обладать прочностными характеристиками φ д ос и c д ос , а при переходе к предельной схеме - критическими характеристиками φ к ос и c к ос . Допущение заключается в том, что, если для какого-то i -го отсека φ д i / φ д ос = εi и c д i / c д ос = μi , то φ к i / φ к ос = εi и c к i / c к ос = μi . Очевидно, каждый участок поверхности скольжения здесь характеризуется своим постоянным значением коэффициентов ε и μ . Кривую связи в данном случае приходится строить в виде кривой
c к ос = f ( φ к ос ) или c к ос = f [( tg φ к )ос]. ( 46)
Учитывая принятые допущения, можем на основании общих выводов [ 34] написать уравнение предельного равновесия для сухого связного неоднородного (в отношении φ д и c д ) грунта в следующем виде:
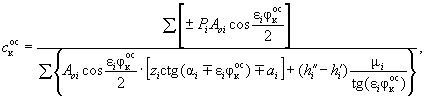 ( 47)
( 47)
где
![]() ( 48)
( 48)
Ясно, что в этих выражениях произведения εiφ к ос и μic к ос представляют собой критические прочностные характеристики грунта в каждом i -ом отсеке. Если эти характеристики φ к i = εiφ к ос и c к i = μic к ос могут быть каким-либо образом определены, то возможно получение уравнений равновесия для основного участка:
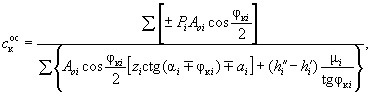 ( 47-а)
( 47-а)
где
![]() ( 48-а)
( 48-а)
Соответственно оползневое давление выразится формулой
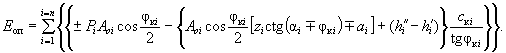 ( 49)
( 49)
В способы учета фильтрационной и сейсмической силы, предложенные Р.Р. Чугаевым, внесем некоторые изменения. Дело в том, что Р.Р. Чугаев рассматривает лишь случаи устойчивости откосов земляных плотин в гидротехническом строительстве. Для таких сооружений учет действия воды, разумеется, гораздо сложнее, чем для естественных склонов с неполным водонасыщением грунта. В гидротехнических сооружениях требуется учитывать действие давления сплошной акватории с одной стороны насыпи, возможность быстрых спадов уровня воды в водохранилище, интенсивную фильтрацию наружу откоса или внутрь его и т.д. Мы же рассматриваем лишь действие грунтовых вод, находящихся в естественном склоне в покое или фильтрующихся наружу откоса (нередко даже в виде отдельных струйчатых потоков). Поэтому мы упростим способ определения гидравлической силы ji , предложенный Р.Р. Чугаевым, и примем его таким же, как и для других рассматриваемых нами методов расчета. Более просто будем учитывать и сейсмические воздействия (также аналогично учету в других методах расчета). В работе же [ 34] Р.Р. Чугаев предлагает особый способ расчета устойчивости откоса с учетом сейсмических сил, названный им способом поворота откоса (см. выше). В процессе указанных упрощений отдельно наклон рассматриваемых сил не будем учитывать, так как значительное усложнение расчета не оправдывается получаемым уточнением.
При таких допущениях уравнение предельного равновесия и формула оползневого давления для связного неоднородного грунта с учетом гидродинамической и сейсмической сил выразятся выражениями
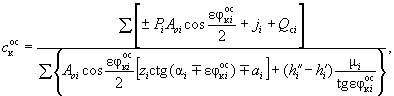 ( 50)
( 50)
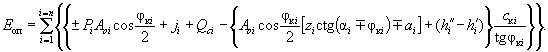 ( 51)
( 51)
Расчет устойчивости откоса (определение коэффициента устойчивости K у ) по методу Р.Р. Чугаева (при использовании способа наклонных сил) строится следующим образом: исходя из соответствующего уравнения предельного равновесия, составленного для рассматриваемого оползневого блока, находится величина tg φ к (или φ к ), затем по формуле ( 38-а) или ( 38-б) вычисляется искомая величина K у .
При этом, как правило, расчету следует подвергать не заданный оползневой блок, а несколько упрощенную его схему: различные детали, касающиеся, например, очертания откоса или грунтов, слагающих его тело, при расчете следует опускать, если заранее очевидно, что они не могут существенно влиять на окончательные результаты расчета. При вычислении tg φ к (или φ к ) обычно применяется способ пробных попыток. Для этого можем, например, использовать графический прием, представив уравнение предельного равновесия в виде функции F (φк). Особенно это удобно в случае однородного сыпучего грунта, когда c к = 0. Тогда величину F (φк) подсчитывают для различных углов φк и строят кривую F (φк) на графике зависимости F (φк) от φк. Искомое значение φк будет то, при котором величина F (φк) обращается в нуль.
Однако возможно определять K у сразу, без промежуточного определения φк. В таком случае коэффициент устойчивости склона определяется (подбором или графически) из уравнения
F 1 ( K у ) = F 2 ( K у ), ( 52)
где (учитывая выражения ( 38-а ) и ( 38-б ))
F 1 ( K у ) = 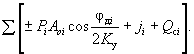 ( 53)
( 53)
F 2 ( K у ) =
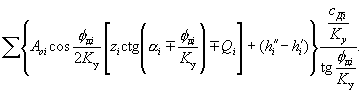 ( 54)
( 54)
В этих зависимостях
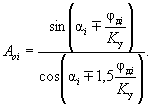 ( 55 )
( 55 )
Далее, задаваясь различными значениями K у = 1,0; 1,1; 1,2; 1,3; 1,4, на общем графике строятся кривые функций F 1 ( K у ) и F 2 ( K у ). Точка пересечения этих кривых (рис. 7) дает искомое значение K у . То есть коэффициент устойчивости K у рассматриваемого склона равен значению, при котором становятся тождественно равными функции F 1 ( K у ) и F 2 ( K у ) .
Для однородных грунтов уравнение предельного равновесия будет иметь вид
![]() ( 56)
( 56)
где
![]()
В таком случае имеется еще один способ определения коэффициента устойчивости K у . Для этого по уравнению ( 56) строят график-кривую связи (см. рис. 5), задаваясь произвольными значениями φк и определяя c к . Все точки кривой связи для данного оползневого блока удовлетворяют условию K у = 1. На график наносится также точка п с нормативными значениями tg φ и c , через которую проводится линия, параллельная кривой связи и луч on через начало координат 0 графика. Далее коэффициент устойчивости склона определяется по одному из соотношений:
![]() ( 57 )
( 57 )
При заданном K у (то есть при проектировании удерживающих конструкций, обеспечивающих требуемый коэффициент запаса устойчивости по сравнению с предельным состоянием) оползневое давление может быть представлено выражением
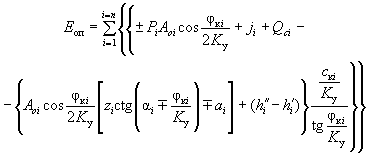 , ( 58 )
, ( 58 )
где
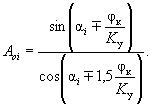 ( 59)
( 59)
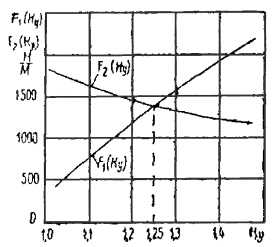
Рис. 7 . Определение K у методом Р.Р. Чугаева
В данном выражении φ к i и c к i - значения прочностных характеристик грунта, определенные натурными методами для каждого из отсеков оползневого блока, требующего укрепления (то есть находящегося в состоянии, близком к предельному). Если же предполагается укрепление склона, состояние которого в данный момент устойчиво, но может приблизиться к предельному в результате внешних воздействий (подрезка склона, нагружение его и т.д.), то для таких условий натурно устанавливаются φд и c д , а затем определяются φ к и c к с помощью уравнения предельного равновесия (методом пробных попыток).
Подсчитывать давление при K у = 1 и затем умножать итоговую цифру на коэффициент устойчивости нельзя, так как это неизбежно занижает суммарную величину оползневого давления. При последовательном суммировании по уравнению ( 58) величин для каждого последующего сечения следует проверять знак получаемой суммы. Если для какого-либо сечения результирующая сумма будет равна нулю или приобретет отрицательный знак, отсеки выше этого сечения при суммировании не учитываются, так как имеют собственный запас устойчивости (равный или больший требуемого) и не оказывают давления на нижележащие участки.
Рассмотренный метод Р.Р. Чугаева имеет важное теоретическое значение. Однако в практическом смысле он более применим, как мы уже видели, для искусственных откосов гидротехнических сооружений. Для расчета устойчивости естественных оползневых склонов его использование менее оправдано по следующим причинам. Метод исходит из того, что в момент расчета устойчивости откоса прочностные характеристики слагающего его грунта более критических - тех, которые возникнут в этом же грунте при достижении им состояния предельного равновесия. То есть, рассчитывается откос, коэффициент устойчивости которого, как правило, более единицы. Проектирование же удерживающих конструкций и противооползневых мероприятий ведется обычно для укрепления неустойчивых или опасных в оползневом отношении склонов, у которых обычно коэффициент устойчивости менее или близок к единице, а значения определенных натурным путем в данный момент прочностных характеристик близки к критическим. По сути, в таком случае нам известны φк и c к и неизвестны φ д и c д , то есть K у этим методом определить невозможно. Разумеется, можно возразить, что при наличии φ к и c к коэффициент устойчивости должен равняться единице. Однако вспомнив наше допущение о применении принципов теории предельного равновесия к запредельному состоянию, поймем, что коэффициент устойчивости склона (с конфигурацией, которую мы ему собираемся придать, восстановив после оползания и укрепив удерживающей конструкцией) может быть и менее единицы. Следовательно, применять метод Р.Р. Чугаева для расчета коэффициента устойчивости неустойчивых или малоустойчивых склонов, без дополнительных преобразований, несколько неверно.
Способ же определения оползневого давления по написанной выше формуле ( 58) следует опробовать в сравнении с другими рассматриваемыми в данной работе методами.
Несколько теряет метод Р.Р. Чугаева и в том отношении, что уравнение предельного равновесия решается (в отношении φк и K у ) методом подбора. Кроме того, методы учета действия гидродинамической и сейсмической сил, вполне приемлемые для случаев расчета гидротехнических сооружений (для которых они и разработаны Р.Р. Чугаевым), для расчета обычных естественных склонов неоправданно сложны.
2.5 . Метод горизонтальных сил
Другие употребляемые названия этого способа расчета [ 13, 15, 24, 26]: метод Маслова-Берера, шанхайский метод, метод горизонтальных сил Маслова. Применяется в случаях, когда откос сложен разнородными грунтами и оползень происходит по известной произвольной поверхности скольжения. Предполагается, что эта поверхность скольжения (положение и очертание) уже установлена хотя бы на части ее простирания каким-либо из опытных или теоретических способов. На неизвестной части поверхность скольжения устанавливается методом подбора. В условиях плоской задачи эта криволинейная поверхность скольжения с некоторым приближением может быть заменена в плоскости чертежа той или иной совокупностью прямых линий - линий скольжения. В соответствии с этим весь массив грунта возможно разбить на отдельные отсеки. Практически поступают наоборот: массив грунта разделяют на отдельные отсеки из таких соображений, чтобы каждый расчетный отсек состоял, по возможности, из более-менее однородного грунта (для простоты вычислений). Каждую линию скольжения в отдельном отсеке принимают за прямую линию (рис. 8, б).
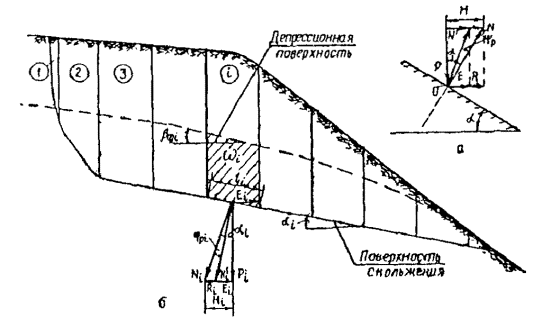
Рис. 8 . Метод горизонтальных сил:
а - основной принцип; б - использование для расчета устойчивости склона
На рисунке 8, а сила N - нормальная к поверхности скольжения составляющая реакции веса P некоторого выделенного расчетного отсека, при условии, что φ = 0 и c = 0. Сила N ' - также реакция P , по при наличии в грунте на поверхности скольжения трения и сцепления; направление силы N ' определяется углом трения φ или углом сдвига Ψ р при наличии в грунте сцепления ( c ≠ 0).
Сила H как проекция на горизонтальную ось силы N представляет собой распор, т.е. давление на вертикальную стенку выделенного по рис. 8, б нижерасположенного отсека при отсутствии в грунте трения и сцепления. Сила R - часть распора H , воспринимаемая трением и сцеплением; E - непогашенная часть распора H .
Очевидно, что
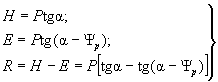 ( 60)
( 60)
Напомним, что угол сопротивления сдвигу Ψ р = arctg F р , где F р - коэффициент сопротивления сдвигу, определяемый по формуле
F р = tg φ + c/σn. ( 61)
Эта формула получена из уравнения прочности
τn = σntg φ + c = σn ( tg φ + c / σn ) = σn F р , ( 62)
причем в каждом отсеке
σni = (Picos αi)/li. ( 63)
Знак силы Hi определяется знаком угла наклона поверхности скольжения αi к горизонту. При совпадении направлений поверхности скольжения и самого откоса угол αi , а следовательно и горизонтальная сила Hi , имеют положительное значение, и наоборот.
Располагая величинами Σ Hi и ΣRi по отсекам всего оползне ного блока мы можем вычислить отвечающий ему коэффициент запаса устойчивости (с учетом сейсмических сил):
K у = ΣRi /( Σ Hi + ΣQci ). ( 64)
При наличии в склоне фильтрационного потока он вызывает на оползающие массы грунта дополнительное давление j , определяемое по формуле (в условиях плоской задачи)
ji = γωωisin β ф i . ( 65)
Направление линии действия фильтрационной силы ji в пределах каждого из отсеков принимается параллельным кривой депрессии в данном отсеке. Таким образом определяется угол β ф i , который образует линия действия ji с горизонтом. Коэффициент запаса устойчивости K у оползневого тела в данном случае (при учете фильтрационного давления) будет определяться следующим выражением:
K у = ΣRi /( Σ Hi + Σjicos β ф i + ΣQci ). ( 66)
В развернутом виде формулы вычисления коэффициента устойчивости методом горизонтальных сил имеют следующий вид.
Без учета фильтрационного давления
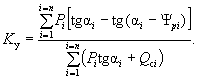 ( 67-а)
( 67-а)
С учетом фильтрационного давления
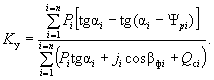 ( 67-б)
( 67-б)
Горизонтальное давление Ei от расчетного отсека на нижерасположенный (см. рис. 8, б) будет равно разности между распором Hi и силой сопротивления Ri . Используя формулы коэффициента устойчивости, мы получим следующее выражение для горизонтального давления:
Ei = K у (Hi + Qci) - Ri, ( 68)
а при наличии фильтрационного давления:
Ei = K у ( Hi + ji cos β ф i + Qci ) - Ri . ( 69)
Направление сейсмической силы, как и в предыдущих методах расчета, в запас принимаем совпадающим с направлением основной сдвигающей силы. Следовательно, суммарное горизонтальное оползневое давление будет равно:
без учета фильтрационного давления
E оп = K у Σ Pi tg αi + K у Σ Qci - Σ Pi tg αi + ΣPitg ( αi - Ψpi ) = ( K у - 1) ΣPitg αi + K у Σ Qci + ΣPi tg ( αi - Ψpi );
E оп = ![]() ( 70-а)
( 70-а)
с учетом фильтрационного давления
E оп = K у Σ Pi tg αi + K у Σ ji cos β ф i + K у Σ Qci - Σ Pi tg αi + ΣPitg ( αi - Ψpi ) = ( K у - 1) ΣPitg αi + K у Σ ji cos β ф i + K у Σ Qci + ΣPi tg ( αi - Ψpi );
E оп = ![]() ( 70-б)
( 70-б)
Как видно из написанных формул, при определении E оп мы сдвигающие силы умножаем на коэффициент устойчивости K у , чтобы удерживающую конструкцию рассчитывать на расчетные усилия, а не на фактическое давление. В таком случае величина K у принимается в зависимости от класса всего сооружения, типа склона, грунтовых условий и т.д. (см. выражение ( 3) и подраздел 5.3), и его в написанных выражениях следует обозначать через K у э .
Следует отметить, что при определении E оп суммирование по отсекам необходимо вести последовательно, начиная с самого верхнего, для того чтобы выполнялось основное уравнение статики. Подробнее этот вопрос будет разобран при рассмотрении аналитического метода Г.М. Шахунянца.
При вычислении Kу или E оп при наличии грунтовых вод (в любом виде) для определения угла сдвига Ψр i принимаются сдвиговые характеристики c в i и φв i для грунта в замоченном состоянии.
Как и ранее, при значительном расхождении между наклонами депрессионной кривой (фильтрационного давления) и поверхности скольжения, после нахождения величины и направления равнодействующей сил фильтрационного давления на каждый расчетный отсек, рекомендуется учитывать уменьшение веса расчетного отсека на величину вертикальной составляющей равнодействующей гидродинамического давления и увеличение горизонтального сдвигающего усилия на величину горизонтальной составляющей этого давления (с учетом изменения гидравлического градиента в разных направлениях).
Метод горизонтальных сил весьма эффективен для условий рассматриваемой нами задачи, поскольку дает возможность определения величины результирующей сдвигающих и удерживающих сил для случая разнородной оползневой толщи грунтов и произвольного очертания поверхности скольжения. Причем метод этот выгодно использовать, когда контуры поверхности скольжения определены недостаточно четко. Например, когда поверхность скольжения частично совпадает с какой-либо ослабленной поверхностью, которая не выходит на поверхность земли или выходит далеко от бровки склона.
2.6 . Метод касательных сил
Употребляемые названия метода и его разновидностей [ 14, 15, 17, 19, 24, 30, 38, 39]: обычный метод, метод Г.М. Шахунянца, метод прислоненных отсеков, метод Петерсона, метод алгебраического суммирования, метод плоских поверхностей сдвига, метод алгебраического сложения сил, метод прислоненного откоса и т.д.
Метод наиболее часто применяется, когда поверхность скольжения каким-либо из имеющихся методов четко определена на всем протяжении. Например, когда делювий сползает по коренным породам, и кровля последних принимается за поверхность скольжения. В таком случае удобно учитывать фактически сдвигающие силы, направленные по касательной к поверхности скольжения. При этом поверхность скольжения представляют состоящей из ряда плоских участков, то есть в виде ломаной линии.
Г.М. Шахунянц, например, предложил использовать для определения коэффициента устойчивости массива грунта, сползающего по фиксированной поверхности скольжения, формулу, полученную для круглоцилиндрической поверхности:
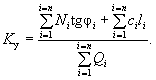 ( 71 )
( 71 )
К такому способу обращались и многие другие авторы, хотя математически он не совсем строг: в данном случае иногда складываются разнонаправленные силы.
Обращаясь к разложению сил, представленному на рис. 9, а, с учетом сейсмического воздействия получим:
при отсутствии грунтовых вод
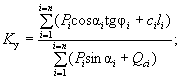 ( 72-а)
( 72-а)
при простом затоплении склона
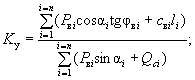 ( 72-б)
( 72-б)
при воздействии на склон фильтрационного потока
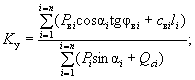 ( 72-в)
( 72-в)
Как и ранее, вес грунта с учетом взвешивания равен (при протяженности вырезанного участка склона, равной единице)
P в i = γ i lih ср. i - γ ω lihi = ( γ i h ср. i - γ ω hi ) li . ( 73)
Вес грунта без учета взвешивания
Pi = γ i lih ср. i . ( 74)
Если в пределах рассматриваемого отсека (на поверхности склона или на бровке) находятся какие-либо сооружения, то их вес следует добавлять к весу грунта в данном отсеке.
В частном случае, когда фиксированная поверхность скольжения всего оползня плоская, как представлено на рис. 9, а , в написанных формулах тригонометрические функции угла наклона этой поверхности к горизонту ( sin α и cos α) могут быть вынесены за знак суммы. Тогда в случае однородного грунта (постоянные сдвиговые характеристики) для всей оползающей призмы формула оползневого давления имеет простой вид (при отсутствии грунтовых вод):
E оп = K у ( P sin α + Q с ) - tg φ P cos α - cL , ( 75)
где P - вес всей сползающей призмы;
L - длина плоскости скольжения.
Чаще же на практике бывает, что поверхность скольжения не является плоской, а может быть представлена из отдельных участков, имеющих различные наклоны к горизонту. В этом случае удобно определять оползневое давление для отдельных отсеков, а затем строить эпюру его изменения.
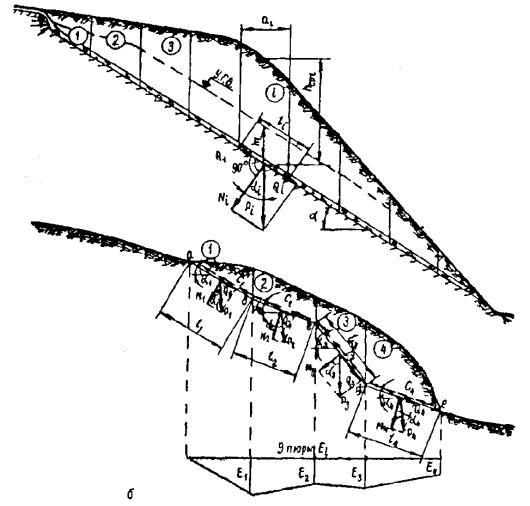
Рис. 9 . Метод касательных сил:
а - случай плоской поверхности скольжения; б - случай ломаной поверхности скольжения
Предположим, что оползневые массы движутся по поверхности abcde (рис. 9, б). Для определения коэффициента устойчивости и величины оползневого давления разбиваем весь оползающий массив на ряд отсеков таким образом, чтобы в пределах каждого отсека поверхность скольжения была плоской. Определяем далее вес каждого отсека Pi и раскладываем его на нормальную и касательную составляющие к плоскости скольжения данного отсека. Для определения оползневого давления рассмотрим условия равновесия отдельных отсеков оползня, взяв сумму проекций внешних сил на направление движения каждого отсека. Для удобства начнем это рассмотрение с верхнего отсека 1 , затем перейдем к соседнему 2 и т.д.
Для отсека 1 надо взять сумму проекций всех сил на плоскость скольжения ab , включая и неизвестное давление со стороны соседнего отсека 2 , и приравнять ее нулю. Таким образом найдем величину реакции E 1 , которая должна быть приложена к отсеку 1 со стороны отсека 2 по направлению ab , чтобы отсек 1 находился в равновесии. Величина E 1 и является оползневым давлением.
Приняв обозначения, указанные на рис. 9, б, найдем (первоначально без учета грунтовых вод и сейсмической силы):
E 1 + tg φ1N1 + c1l1 - Q1 = 0;
E 1 + tg φ1P1cos α1 + c1l1 - P1sin α1 = 0,
откуда получим
E 1 = P 1 sin α1 - tg φ1P1cos α1 - cl1 .
При рассмотрении равновесия отсека 2 необходимо учесть и действие силы E 1 , но с обратным знаком. Точно так же рассматривают условия равновесия для всех остальных отсеков. В общем случае для определения оползневого давления любого отсека оползня будет справедливо выражение:
E i = P i sin αi - tg φiPicos αi - cili + Ei-1, ( 76)
где Ei -1 - проекция оползневого давления предыдущего отсека на направление скольжения рассматриваемого отсека.
Определив величину оползневого давления для отдельных отсеков оползня, по полученным данным строим эпюру оползневых давлений (рис. 9, б), необходимую для выбора по длине оползня места заложения удерживающего сооружения, которое рационально расположить в сечении с минимумом E i . Для получения требуемого запаса устойчивости при вычислении оползневого давления, как и ранее, сдвигающие силы умножаем на расчетный коэффициент устойчивости K у .
В «обычном» методе расчета нередко Ei -1 принимают равным результирующей касательной силе в предыдущем отсеке, а не проекции ее на направление скольжения рассматриваемого отсека. При разнице в углах наклона к горизонту линий поверхности скольжения в соседних отсеках менее 10 % ошибка при таком способе расчета получается незначительной. При резких колебаниях наклона поверхности скольжения этой разницей пренебрегать нельзя. Однако, поскольку мы рассматриваем «Метод касательных сил», напишем формулы для определения оползневого давления в случае простого суммирования касательных сил. Если не забывать о том, что суммирование обязательно должно идти последовательно, начиная с самого верхнего отсека (так, чтобы Ei -1 входило в сумму), то формулы для определения оползневого давления будут иметь следующий вид.
При отсутствии грунтовых вод
E оп = ![]() [ K у э ( P i sin αi + Q с i ) - ( Pi cos αitg φi + cil i )]. ( 77-а)
[ K у э ( P i sin αi + Q с i ) - ( Pi cos αitg φi + cil i )]. ( 77-а)
При простом затоплении склона
E оп = ![]() [ K у э ( P в i sin αi + Q с i ) - ( P в i cos αitg φ в i + c в i l i )]. ( 77-б)
[ K у э ( P в i sin αi + Q с i ) - ( P в i cos αitg φ в i + c в i l i )]. ( 77-б)
При воздействии на склон фильтрационного потока
E оп = ![]() [ K у э ( P i sin αi + Q с i ) - ( P в i cos αitg φ в i + c в i l i )]. ( 77-в)
[ K у э ( P i sin αi + Q с i ) - ( P в i cos αitg φ в i + c в i l i )]. ( 77-в)
2.7 . Аналитический метод Г.М. Шахунянца
Данный метод [ 23, 36, 39], как и предыдущий, удобнее всего применять, когда конфигурация поверхности скольжения на всем протяжении уже установлена. Метод Г.М. Шахунянца в целом аналогичен методу касательных сил, однако в данном случае более строго соблюдены законы строительной механики. Как и ранее, оползневой блок для расчетов мысленно членится на ряд отсеков. Обычно отсеки принимают такими, чтобы без практической потери точности можно было в их пределах принимать поверхность за плоскость и чтобы состояние грунта, очертание склона, действие внешних сил и т.п. были практически однородными.
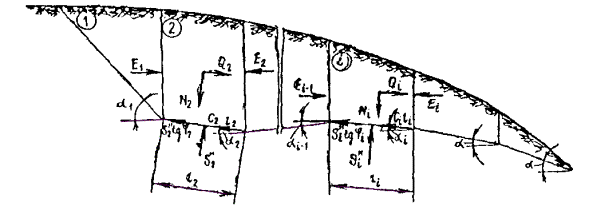
Рис. 10 . Аналитический метод Г.М. Шахунянца
Будем определять устойчивость блока при произвольной поверхности возможного смещения (рис. 10). Рассмотрим условие равновесия любого i -го отсека (например, второго). Все внешние активные силы (вес грунта в отсеке, внешняя нагрузка и т.д.), действующие на i -й отсек, приводим к равнодействующей Pi . Последнюю раскладываем в точке ее приложения на составляющие: нормальную Ni и тангенциальную Qi к плоскости возможного сдвига отсека. Г.М. Шахунянц в общем случае принимает, что равнодействующая внешних активных сил наклонена к вертикали под углом θi . Мы для упрощения рассуждений будем рассматривать случай, когда сила Pi вертикальна, то есть угол θi = 0, тогда
Ni = Picos αi; Qi = Pisin αi. ( 78)
При падении поверхностей скольжения в пределах каждого отсека в сторону возможного смещения блока значения αi берутся со знаком плюс, при падении поверхностей скольжения в обратную сторону - со знаком минус.
Следуя основным законам строительной механики, выделив для раздельного рассмотрения i -й отсек, мы обязаны заменить влияние на него вышележащей части блока силой Ei -1 , а влияние нижележащей части - аналогично силой Ei . В общем случае Г.М. Шахунянц принимает, что сила Ei -1 направлена под некоторым углом ηi -1 к горизонту, сила Ei - под углом ηi к горизонту и т.д. Мы же в данном случае допустим, что силы Ei направлены по прямым, параллельным направлению реакции удерживающей конструкции, которое примем горизонтальным (как это обычно принимается при вертикальности грани контакта грунта с удерживающей конструкцией). Поэтому все силы Ei рассматриваем ориентированными горизонтально, то есть ηi = 0. Сопротивляются сдвигу i -го отсека по плоскости его основания, наклоненной под углом αi к горизонту, сила сцепления cili и сила трения Si н tg φ i (где Si н - нормальная реакция основания).
Так как величина Ei -1 является, как это будет показано далее, известной из расчета предыдущего отсека, то неизвестными силами оказываются лишь Si н и Ei . Для их нахождения достаточно использовать два уравнения статики. Проектируя все силы на нормаль к основанию отсека и на направление самого основания, получим:
Si н = Ni + (Eisin αi - Ei-1sin αi); ( 79)
Qi = cili + Si н tg φi + (Eicos αi - Ei -1 cos αi). ( 80)
Подставляя найденное значение Si н в выражение для Qi и уве личив последнее в K у э раз, получим уравнение для определения Ei :
K у э Qi = Ni tg φi + cili + [ Ei ( cos αi + tg φisin αi ) - Ei -1 ( cos αi + tg φisin αi )]. ( 81)
Значение Qi увеличено в Kуэ раз для того, чтобы обеспечить каждому i -му отсеку в стабилизованном массиве заданный коэффициент устойчивости Kу против сдвига по своему основанию. В этом случае и весь блок возможного смещения будет иметь в целом тот же коэффициент устойчивости.
В дальнейшем эту тангенциальную составляющую Q i внешних активных сил Pi , если она стремится сдвинуть отсек по своему основанию, будем обозначать через Qi -сд . Если та же тангенциальная составляющая Qi направлена в сторону, обратную направлению возможного смещения блока, то она будет уже силой, удерживающей отсек от возможного смещения, и ее не следует увеличивать в K у э раз. Обозначим в этом случае Qi через Qi -уд .
Предыдущее уравнение можно упростить, помня, что
cos αi + tg φisin αi = ( cos αicos φi + sin αisin φi )/ cos φi = cos ( αi - φi )/ cos φi . ( 82)
После сделанных пояснений найдем значение Ei :
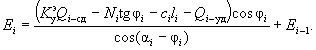 ( 83)
( 83)
Для отсеков, у которых Qi = Qi -сд , в формуле ( 83) следует значения Qi -уд принимать равным нулю; в случаях, когда Qi = Qi -уд , следует принимать равным нулю Qi -сд . Поскольку в большинстве практических случаев направление падения поверхности скольжения по всей протяженности совпадает с направлением возможного смещения оползневого блока (то есть является монотонным), в дальнейших формулах у нас будут фигурировать лишь Qi , которые мы будем подразумевать как Qi -сд , а Qi -уд будем принимать равными нулю. Однако в каждом конкретном случае при выполнении расчетов следует помнить о возможности появления сил Qi -уд .
Реакции Ei части блока, находящейся ниже i - го отсека, в общем случае можно определить последовательными расчетами, идя от первого отсека, для которого Ei -1 равно нулю, к последнему. Последовательное определение сил Ei , особенно целесообразно, когда без расчета невозможно заранее отделить на поперечнике устойчивые части склона от неустойчивых. Первый из отсеков, для которого Ei получилось равным нулю или даже отрицательным, отделяет вышележащую устойчивую часть блока (включая себя) от нижележащей. При недопущении в грунте растягивающих напряжений нижележащая часть должна рассматриваться отдельно. Анализируя последовательно значения Ei , нетрудно установить места возможных разрывов грунта (место перехода от устойчивых к неустойчивым частям блока), места целесообразного расположения удерживающих конструкций (например, места наименьших значений Ei и умеренных значений толщин смещающегося слоя) и т.п.
При принятии Qi -уд = 0 последняя написанная нами формула примет вид:
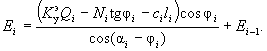 ( 84)
( 84)
Для первого отсека Ei -1 = 0, следовательно
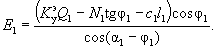
Для второго отсека
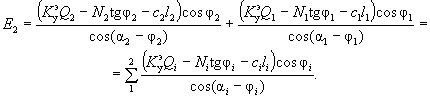
В общем случае оползневое давление равно:
![]() ( 85)
( 85)
Очевидно, что у свободного откоса сила E оп , поддерживающая последний отсек, должна быть равна нулю (так как ничто не поддерживает этот последний отсек). Исходя из этого, можно для свободного откоса получить значение коэффициента устойчивости, приравняв E оп = 0 (в данном случае, когда речь идет о степени устойчивости склона, а не о величине запаса его укреп ления, это будет Kу, а не Kуэ):
![]()
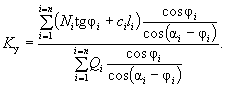 ( 86)
( 86)
Если поверхность возможного смещения - плоскость с неизменными характеристиками φ и c и разбивки на отсеки делать не требуется, то оползневое давление определяется по формуле
![]() ( 87 )
( 87 )
Таким образом можно определить не только активное давление грунта на удерживающее сооружение (обратное по направлению реакции конструкции) E а = E оп , но и пассивное давление (отпор) E о = E оп . Так как при отпоре тангенциальная сила Q становится силой, сопротивляющейся сдвигу, то при этом следует принять K у = 1.
Максимальное значение E а и минимальное значение E о могут быть найдены из
условия ![]() - при отрицательном значении второй
производной в первом случае и положительном во втором.
- при отрицательном значении второй
производной в первом случае и положительном во втором.
Для частного случая обычного кулоновского давления (призма обрушения у подпорной стенки с горизонтальной поверхностью засыпки) при Kу = 1 указанным способом получим общеизвестную формулу:
E оп = (1/2) γH 2 tg 2 (45 ± φ /2) + [ p tg (45 ± φ /2) - c ] H tg (45 ± φ /2), ( 88)
где p - вертикальная нагрузка на засыпку за стенкой. Здесь верхние знаки относятся к случаю E оп = E а , а нижние - к случаю E оп = E о .
Таким образом, метод Г.М. Шахунянца является единым как для расчета коэффициентов устойчивости свободных откосов (склонов), так и для определения сил, передаваемых на удерживающие конструкции.
Величина фильтрационной силы j , при наличии гидродинамического давления, и величина сейсмической силы Q с , при расположении склона в сейсмическом районе, определяются, как и ранее, по формулам
ji = γωωisin β ф i ; Qci = μPi . ( 89)
В этом методе также будем полагать приближенно (в запас), что фильтрационная и сейсмическая силы являются силами сдвигающими (т.е. направленными параллельно основанию отсека).
Вспомнив выражения ( 78) составляющих Ni и Qi через основную силу Pi , получим окончательные формулы для определения коэффициента устойчивости склона и величины оползневого давления. При отсутствии грунтовых вод
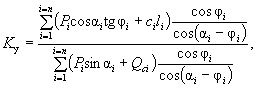 ( 90-а)
( 90-а)
![]() ( 91-а)
( 91-а)
При обычном водонасыщении склона
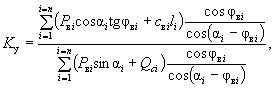 ( 90-б)
( 90-б)
![]() ( 91-б)
( 91-б)
При воздействии на склон фильтрационного потока
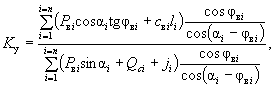 ( 90-в)
( 90-в)
![]() ( 91-в)
( 91-в)
Нередко на практике встречаются случаи воздействия на склон струйчатых потоков грунтовых вод (например, на Южном берегу Крыма или склонах Кавказских гор). В таком случае гидродинамическое давление необходимо учитывать, а взвешивание грунта - не учитывать, так как сплошное насыщение грунтов склона отсутствует. То есть следует применять формулы только с учетом фильтрационного давления:
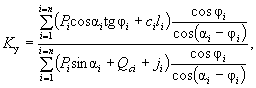 ( 90-г)
( 90-г)
![]() ( 91-г)
( 91-г)
При выводе формул для определения оползневого давления и коэффициента устойчивости были использованы два уравнения статики. Третье условие статики (уравнение моментов) дает возможность определить точку приложения реакции E оп удерживающего сооружения (или силы Ei для любого i -го отсека). Это решение является точным при круглоцилиндрической поверхности скольжения и приблизительным в других случаях. Указанный прием описан при рассмотрении метода многоугольников сил Г.М. Шахунянца.
Написанные расчетные формулы
могут быть использованы также для схемы, учитывающей, что силы E отклонены от горизонтали на
угол η , постоянный для всех отсеков. Поскольку угол η ограничен
величинами 0 < η < ψ ) (где ψ -
угол сдвига), то он может приближенно приниматься равным 0,5 ψ .
Для этой схемы в расчетных формулах выражение ![]() (отвечающее η = 0) заменяется на
(отвечающее η = 0) заменяется на ![]() (где η
= const ).
(где η
= const ).
2.8 . Графоаналитический метод многоугольников сил Г.М. Шахунянца
Если поверхность возможного смещения известна, например, предопределена геологической структурой склона, установлена при выполнении инженерных изысканий или принята с помощью различных теоретических методов, то расчет устойчивости массива нередко целесообразно вести способом многоугольников сил [ 23, 38, 39].
В основе расчета сохраняется гипотеза затвердевшего тела. Эта гипотеза нарушается, если поверхность смещения не плоскость и не поверхность круглого цилиндра (по которым вышележащий массив действительно может смещаться, как одно целое), так как при любом ином очертании поверхности при смещении в массиве возникают местные напряжения. Но эти местные напряжения могут при движении массива создавать лишь чисто местный эффект в виде отдельных трещин разрыва или местных уплотнений грунта. Так как расчет ведется для определения условий устойчивости массива, то представляется возможным сохранить как рабочую гипотезу предположение о затвердевшем теле. Данное предположение лежит в обычных рамках тех допущений, которые приняты практически в обычных расчетах строительной механики. В большом количестве случаев строительных расчетов деталь рассматривается как одно целое и рассчитывается на общие напряжения. Если требуется, то дополнительно учитывается влияние местных напряжений.
Этот способ покажем на примере определения давления на удерживающую конструкцию, исходя из предположения, что без взаимодействия с этим сооружением массив будет малоустойчив или неустойчив.
На рис. 11, а представлен грунтовый массив, на котором имеются какие-либо сооружения (на рисунке не показаны). Массив, поддерживаемый противооползневой конструкцией, находится в равновесии. Необходимо определить давление грунта на удерживающее сооружение, равное по величине и обратное по направлению реакции этого сооружения.
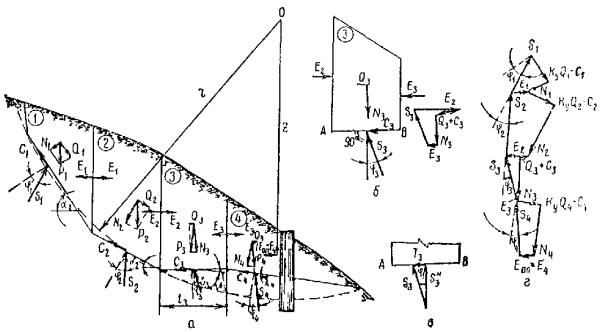
Рис. 11 . Метод многоугольников сил:
а - расчетная схема склона; б - схема одного из отсеков с многоугольником сил; в - деталь подошвы отсека; г - общий многоугольник сил
Разобьем весь массив на ряд отсеков. В веса полученных отсеков Pi включаем вес грунта и сооружений, находящихся над каждым отсеком. На каждый отсек действует тангенциальная Qi и нормальная Ni составляющие веса отсека Pi . Вырежем мысленно какой-либо отсек из массива (например, 3 - см. рис. 11, б) и приложим к нему, кроме указанных сил, силы E 2 и E 3 , заменяющие воздействие на него соседних отсеков. По поверхности АВ возможного смещения отсека действуют реакции со стороны этой поверхности, равные, в условиях предельного равновесия, силам сцепления и трения по этой поверхности (при условии полного проявления этих сил), и нормальная реакция. Силу сцепления обозначим через C 3 = c 3 l 3 . Силу трения T 3 и нормальную реакцию S 3 н поверхности АВ заменим их равнодействующей S 3 (см. рис. 11, в ). Сила трения T 3 = S 3 н tg φ 3 , а равнодействующая
S 3 = ![]() ( 92)
( 92)
Угол наклона равнодействующей S 3 к нормали к поверхности АВ будет при этом равен углу φ 3 внутреннего трения грунта по грунту на поверхности АВ (см. рис. 11, в ), так как тангенс этого угла равен отношению силы трения T 3 = tg φ 3 S 3 н к нормальной реакции S 3 н .
Весь массив будет иметь заданный коэффициент устойчивости Kу, если для каждого отсека будет выдержано это же требование.
Силами, сдвигающими весь массив по поверхности скольжения, будут тангенциальные составляющие Qi сил Pi , если они направлены в сторону возможного смещения массива. Все остальные силы, в том числе и реакция удерживающего сооружения, являются силами либо непосредственно не влияющими на устойчивость (как силы Ni ), либо сопротивляющимися возможному смещению.
Рассматриваем коэффициент устойчивости в отношении возможного смещения каждого отсека по поверхности скольжения (принимаемой для каждого отсека за плоскость) как отношение всех тангенциальных сил, удерживающих массив ( R уд ), ко всем тангенциальным силам, стремящимся вызвать смещение его ( Q сдв ). Тогда можно записать, что для обеспечения заданного коэффициента устойчивости необходимо, чтобы
R уд - Kу Q сдв = 0 (Kу = R уд / Q сдв ; R уд = Kу/ Q сдв ). ( 93)
Иначе говоря, задачу обеспечения заданного коэффициента устойчивости Kу можно свести к обычным условиям равновесия, если при рассмотрении действия сил вместо сдвигающих тангенциальных сил брать силы в Kу раз большие по величине и действующие в том же направлении.
Поэтому принимаем при составлении условий равновесия вместо тангенциальной составляющей Qi силы Pi величину K у Qi , если сила Qi стремится сдвинуть массив (как это имеет место в отсеках 1, 2 и 4). Значение силы Qi принимается без изменения, если она сопротивляется смещению (как это имеет место в отсеке 3).
При проведении расчета допускаем, что силы Ei направлены по прямым, параллельным направлению реакции удерживающего сооружения E оп . На рис. 11, а реакция E оп противооползневой конструкции принята направленной горизонтально, поэтому все силы Ei ориентированы горизонтально.
Решая задачу относительно каждого отсека самостоятельно (см. рис. 11, б), следует считать для каждого отсека силы Qi , Ci и E i-1 известными. При этом сила E i-1 известна в результате решения задачи для предыдущего отсека, имея в виду, что в первом отсеке сила отсутствует. Неизвестными силами в каждом отсеке являются, следовательно, силы Ei и Si .
Оставляя на время в стороне вопрос определения точек приложения сил, решим задачу по определению величин сил Ei и Si , которые заданы своими направлениями. Для этого достаточно двух условий статики. Эта задача может быть решена как аналитически (см. предыдущий способ расчета), так и построением многоугольника сил. Последнее решение обычно гарантирует достаточную точность. Оно и показано для третьего отсека на рис. 11, б. Для всего склона задача решается графически от отсека к отсеку, построением для каждого из них многоугольника сил. На рис. 11, г эти многоугольники показаны непрерывно следующими один за другим с общей стороной многоугольников Ei - для данного отсека и предыдущего. При переходе от одного отсека к другому следует лишь менять направление силы Ei -1 (являющейся реакцией данного отсека на предыдущий) на обратное, так как в этом случае сила Ei -1 передается от предыдущего отсека на данный.
Сила E 4 , определенная для последнего отсека, и будет представлять собой полную реакцию, которую должно обеспечить удерживающее сооружение, чтобы массив имел заданный коэффициент устойчивости Kу.
В связи с этим при расчете самого удерживающего сооружения следует требовать лишь выполнения обычных условий равновесия, ибо коэффициент устойчивости уже учтен при определении силы E оп .
Точку приложения реакции удерживающего сооружения E оп , уже известной по величине и направлению, можно приблизительно найти, используя оставшееся третье условие равновесия. Для этого следует найти центр круговой кривой, возможно ближе совпадающей с фактической кривой скольжения (на рис. 11, а заменяющая дуга круга радиуса r с центром О показана пунктиром). Плечо от центра О до направления силы E оп - реакции удерживающего сооружения - обозначено через z .
Беря момент всех сил относительно центра О , получим:
E оп × z = r (Kу ΣQi сдв - Σ C i - ΣSisin φi - ΣNitg φi - ΣQi уд );
z = (Kу ΣQi сдв - Σ C i - ΣSisin φi - ΣNitg φi - ΣQi уд ) × r / E оп . ( 94)
Многоугольник сил дает возможность определять также и наилучшее место расположения удерживающего сооружения, и места наиболее вероятных разрывов массива, и места возможных возникновений бугров и террас выпирания в случае сползания массива (то есть при Kу ≤ 1), и ряд других вопросов, представляющих на практике нередко большой интерес.
Из рассмотрения рисунка 11, г видно, например, что более рациональным было бы расположение удерживающей конструкции на границе не четвертого, а третьего отсека, так как при этом была бы меньше реакция E оп , ибо она равнялась бы E 3 , а не E 4 (а из многоугольника сил видно, что E 3 < E 4 ).
При построении многоугольника сил необходимо следить за тем, не становится ли в каком-то i -ом отсеке сила равной нулю или обратного знака, то есть не исчезает ли она или даже не становится ли вместо силы поддерживающей силой сдвигающей. Последнее физически быть не может (если в грунте не могут возникать растягивающие напряжения) и покажет лишь, что часть массива от начала и до границы где-то внутри данного отсека имеет не только заданный коэффициент устойчивости, но даже избыток. Таким образом, при построении многоугольника сил непосредственно определяются границы устойчивых участков массива. При наличии отрицательного значения силы (когда она имеет направление в i -ом отсеке в сторону смещения) и построении многоугольника сил для следующего отсека i + 1 сила Ei в этот многоугольник не включается (при условии недопущения растягивающих напряжений; при допущении растягивающих напряжений может учитываться лишь та часть силы Ei , при которой растягивающие напряжения не превосходят допускаемых).
Описанный прием построения многоугольников сил может быть применен и для решения задачи: имеет ли данный массив коэффициент устойчивости не менее заданного?
Если массив не будет иметь заданного коэффициента устойчивости Kу, то сила E оп , равная, например, в рассмотренном случае E 4 , которую надо приложить в конце последнего отсека, чтобы обеспечить массиву этот коэффициент, будет направлена на поддержание массива. Если фактический коэффициент устойчивости массива равен или более заданного, то сила E оп = E 4 будет или равна нулю или направлена в сторону возможного смещения массива. Последнее показывает, что для того, чтобы фактически большой коэффициент устойчивости снизить до заданного, нужно приложить сдвигающую силу E оп = E 4 . В разобранном примере массив не имеет заданного коэффициента устойчивости Kу, так как сила E оп = E 4 в многоугольнике сил оказалась направленной на поддержание откоса.
При наличии на склоне грунтовых вод или необходимости учета сейсмического воздействия силы ji и Q с i добавляются непосредственно к силам Qi и таким образом также участвуют в графическом построении. Взвешивание грунта учитывается аналогично тому, как это было описано в предыдущих методах расчета.
Как видно из сказанного, рассмотренный метод многоугольников сил дает возможность непосредственно определять величину оползневого давления, на которое должна рассчитываться противооползневая удерживающая конструкция.
2.9 . Ускоренный способ расчета методом Г.М. Шахунянца
Как показала практика расчетов, выполнявшихся при проектировании противооползневых удерживающих конструкций глубокого заложения, аналитический метод Г.М. Шахунянца весьма эффективен. Сооружения, рассчитанные на оползневое давление, вычисленное данным методом, нормально эксплуатируются в течение ряда лет. Особенно удобно применение написанных выше формул при использовании ЭЦВМ. В таком случае вычисления по разработанным типовым программам требуют минимальных трудовых затрат.
Однако нередко еще приходится выполнять указанные расчеты вручную (при отсутствии ЭВМ, при выполнении прикидочных расчетов, при сравнении вариантов, при выполнении расчетных прикидок непосредственно в натуре в процессе обследования оползней, при решении вопроса о возможности установки механизмов на склоне и т.д.), когда требуется оперативный счет и нет смысла или возможности выходить на машину. В таком случае формулы Г.М. Шахунянца выгодно применять в несколько преобразованном виде, предложенном автором данной работы [ 3].
Напишем для склона, представленного на рис. 12, выведенную ранее формулу ( 91-г)
![]()
Подставив в это уравнение значения: Pi = γi aih ср. i (причем γi должно учитывать не только объемный вес грунта, но и вес внешней нагрузки на отсеке при ее наличии); Q с i = γωaih ср. i μ ; ji = γωaihisin β ф i , после несложных преобразований получим
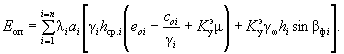 ( 95)
( 95)
Здесь обозначены:
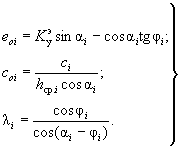 ( 96)
( 96)
Для этих трех соотношений с помощью ЭЦВМ могут быть построены графики по типу представленных на рисунках 13, 14, 15, облегчающие выполнение вычислений.
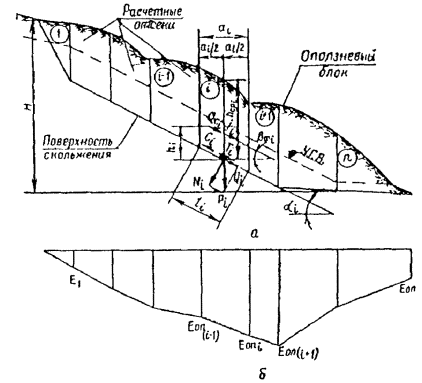
Рис. 12 . Ускоренный способ расчета методом Г.М. Шахунянца:
а - общая расчетная схема склона; б - эпюра оползневого давления
Из графика на рис. 13 ясна интересная деталь: при возрастании угла наклона поверхности скольжения α влияние изменения угла внутреннего трения φ уменьшается. Это естественно, ибо при возрастании угла α основную роль начинают играть силы гравитации, не зависящие от прочностных характеристик грунтов.
Если при выполнении реальных расчетов конкретный склон не уложится в приведенное выше допущение о монотонности поверхности скольжения и в каком-то отсеке она окажется не ниспадающей, а восходящей, то это может быть учтено принятием eoi из графика на рис. 13 при отрицательном угле αi .
При сплошном водонасыщении грунта, где это требуется, следует принимать физико-механические характеристики пород с учетом их замачивания водой: γ в i , c в i , φ в i . В таком случае сейсмические силы следует учитывать не только от веса грунта, но аналогичным образом и от веса воды.
Кроме приведенных графиков, автором данной работы составлены табл. 1 - 3 (см. приложение), способствующие выполнению достаточно точных расчетов. Кроме того, в таблицах приведены необходимые данные для более широкого, чем в графиках, диапазона исходных параметров.
При расположении склона в несейсмическом районе принима ется μ = 0, при отсутствии потока грунтовых вод - h i = 0. В таком случае формула ( 95) принимает вид:
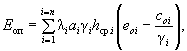 ( 97-а)
( 97-а)
или, что то же самое
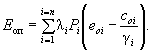 ( 97-б)
( 97-б)
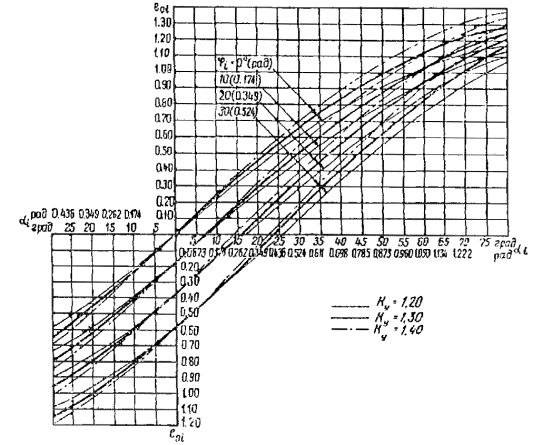
Рис. 13 . Графики зависимости eoi = Kуэ sin αi - cos α i tg φi
При пользовании приведенными выражениями следует помнить, что для определения полного оползневого давления в конце i -го отсека от части оползневого блока, расположенной выше по склону, необходимо последовательно суммировать все оползневые давления от каждого из вышележащих отсеков, начиная с первого (самого верхнего):
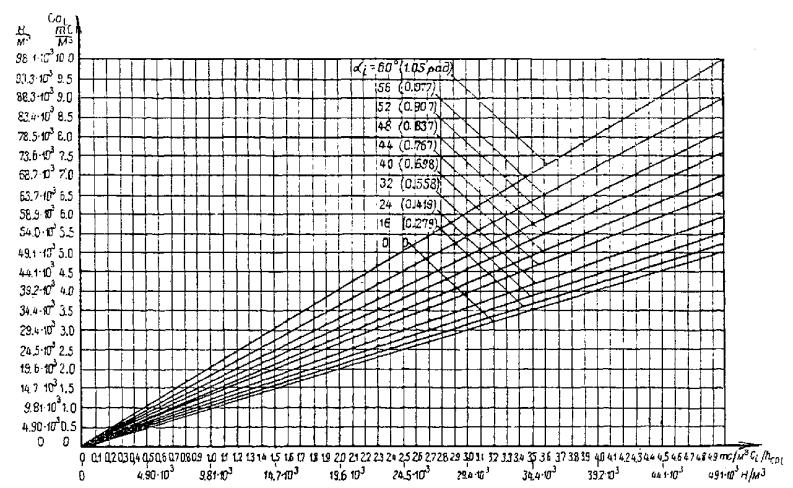
Рис. 14 . Графики зависимости coi = c i /( h ср. i cos αi )
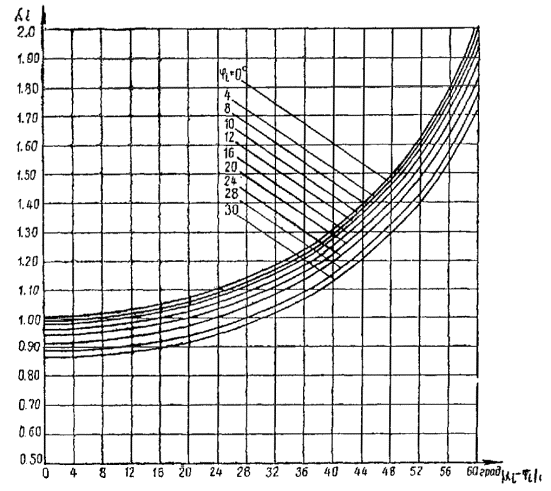
Рис. 15 . Графики зависимости λi = cos φi / cos ( αi - φi )
![]() ( 98)
( 98)
С помощью этих формул строится эпюра оползневого давления по длине всего склона (см. рис. 12, б). Вычисления при этом рекомендуется выполнять, используя заготовки табл. 2 и 3.
Несколько упрощена при этом способе может быть и формула ( 90-г) для определения коэффициента устойчивости склона. После несложных преобразований она приобретает следующий вид. В общем случае:
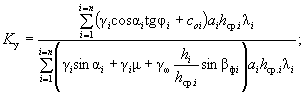 ( 99-а)
( 99-а)
при отсутствии грунтовых вод, в несейсмических районах:
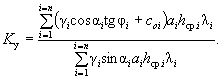 ( 99-б)
( 99-б)
Вычисления коэффициента устойчивости рекомендуется выполнять, используя заготовки табл. 4 и 5.
Таблица 2
Вычисление оползневого
давления по формуле ( 95) 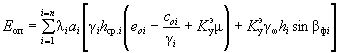

Таблица 3
Вычисление оползневого давления по формуле
( 97-а)
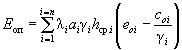

Таблица 4
Вычисление коэффициента устойчивости склона
по формуле ( 99-а) 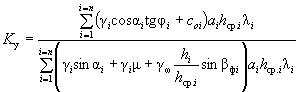

Таблица 5
Вычисление коэффициента устойчивости склона по формуле
( 99-б) 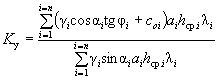

2.10 . Графостатический метод Л.Л. Перковского
Данный метод, по мнению его автора [ 19], удовлетворяет двум требованиям, которым не отвечает большинство иных методов расчета:
а) учитывается взаимодействие между отсеками;
б) удовлетворяются основные три уравнения статики: Σ x = 0; Σy = 0; ΣM = 0 (а не только одно и то не в полной мере, как это имеет место, например, в методе круглоцилиндрической поверхности скольжения).
Сущность его заключается в том, что для выяснения состояния устойчивости земляного массива строится многоугольник сил. Если он замыкается, то имеется или равновесие массива, или случай равномерного движения. Если в многоугольнике последняя сила (эта сила реактивная) не достигает точки замыкания (точка О на рис. 16), то это значит, что массив неустойчив, что имеется избыток сдвигающих сил, что должно быть движение; если последняя сила перейдет за точку замыкания, то здесь налицо избыток удерживающих сил, т.е. K у > 1, но движения не будет, так как это избыток пассивных, реактивных сил.
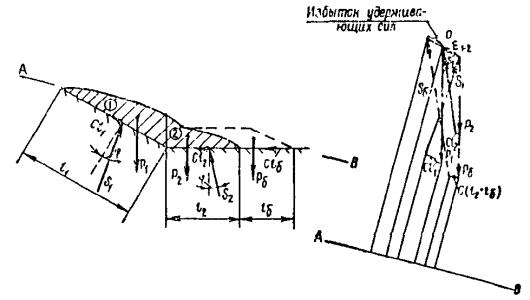
Рис. 16 . Графостатический метод Л.Л. Перковского
Построение силового многоугольника в графостатическом методе базируется на положении, что силы взаимодействия между расчетными отсеками направлены параллельно поверхности скольжения. Кроме того, здесь коэффициент устойчивости определяется непосредственно из многоугольника сил путем проектирования всех действующих на массив сил на некоторую условную линию АВ (см. рис. 16) - линию общего направления смещения - и исчисления отношения между суммами удерживающих и сдвигающих проекций сил.
На рис. 16 приведен схематизированный разрез оползневого массива, усиленного контрбанкетом. Здесь же показан многоугольник сил. Контрбанкет и относящаяся к нему часть силового многоугольника нанесены пунктиром.
Из рис. 16 видно, что при отсутствии контрбанкета многоугольник сил замкнут ( K у = 1); после сооружения контрбанкета многоугольник сил делается незамкнутым - «последняя сила зашла за точку О», т.е. появился избыток удерживающих сил и K у превысил единицу.
Вследствие того, что графостатический метод учитывает взаимодействие между отсеками, коэффициент устойчивости становится больше, чем в случае определения его, например, по обычному методу.
Следует отметить и недостатки рассмотренного метода:
условность выбора линии общего направления смещения, на которую проектируются все силы (и от которой, следовательно, зависят величины проекций и соотношений между ними);
сложность получаемого многоугольника сил при большом количестве отсеков;
отсутствие в прямом виде итоговой величины оползневого давления ( E оп ) на многоугольнике сил (как, например, в методе Г.М. Шахунянца);
отсутствие четкости и простоты из-за необходимости снятия по масштабу величин проекций, иногда накладывающихся одна на другую на линии АВ ;
трудность учета действия грунтовых вод.
2.11 . Метод блока и призм
Нередко непосредственно в основании откоса залегает пласт грунта с ярко выраженной пониженной сопротивляемостью сдвигу. В такой обстановке могут возникнуть условия, способствующие поступательному перемещению оползневого массива больше, чем вращательному. Для подобных условий применяется метод блока и призм [ 29].
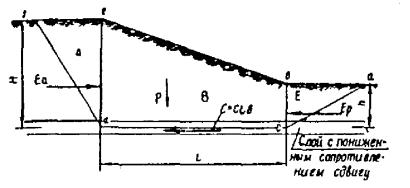
Рис. 17 . Метод блока и призм (расчетная схема)
В этом случае принимается, что оползневой массив слагается из центрального блока В и двух призм А и Е (рис. 17). Центральный блок В выполняет до некоторой степени функции гравитационной подпорной стенки, которая поддерживает толщу грунта, находящегося с левой стороны по грани ed . Вес грунта в призме А оказывает на центральный блок В боковое давление, которое известно под названием активного давления. Очевидно, что это давление стремится вызвать поступательное движение блока В . Этому движению противодействует пассивное давление (отпор), развиваемое призмой Е , а также сопротивление сдвигу по подошве центрального блока. При этом условии коэффициент запаса устойчивости откоса может быть определен по выражению
K у = (cLb + Ptg φ + E р )/Ea , ( 100)
где P - вес блока В толщиной b ;
E р - пассивное давление (отпор), действующее на блок В ;
Ea - активное давление на блок В .
Остальные обозначения прежние.
Для упрощенных условий последние величины определяются по выражениям
![]()
![]() ( 101)
( 101)
Оползневое давление по данному методу может быть определено следующим образом (примем b = 1,0):
E оп = Ea - cL - P tg φ - E р = ![]() - cL
- P tg φ . ( 102-а)
- cL
- P tg φ . ( 102-а)
При наличии сейсмического воздействия и напорных грунтовых вод выражение примет вид:
E оп = ![]() + Qc + j
+ Qc + j ![]() - cL
- P tg φ . ( 102-б)
- cL
- P tg φ . ( 102-б)
Естественно, данный метод применим лишь при несложной конфигурации поперечного сечения склона и пологом залегании пласта грунта с пониженной сопротивляемостью сдвигу. Ввиду его простоты метод может применяться для прикидочных расчетов.
2.12 . Метод Л.П. Ясюнас
Способ [ 12, 40] состоит в следующем: предполагается, что все оползневые массы движутся единым массивом по поверхности скольжения. Для определения оползневого давления рассматриваются условия равновесия оползневого массива в проекциях всех сил на направление движения.
Данный метод разработан для консеквентных оползней.
Для проведения расчета устойчивости весь оползень (рассматривается, как и ранее, 1 м ширины его) в соответствии с характером поверхности скольжения делится на отсеки (рис. 18), в пределах которых след поверхности скольжения может быть принят за прямую. Далее в каждом отсеке определяется вес ( Pi = γi aih ср. i ), тангенциальная ( Qi = Pi sin αi ) и нормальная ( Ni = Pi cos αi ) его составляющие и удерживающие силы: трения ( Ti = Ni tg φi ) и сцепления ( Ci = cili ).
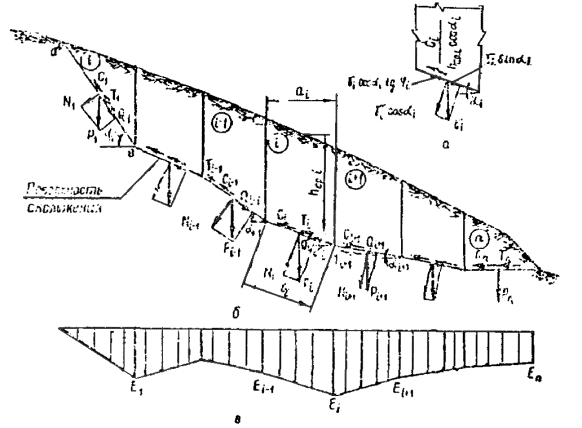
Рис. 18 . Метод Л.П. Ясюнас:
а - схема элементарного объема; б - схема оползневого склона; в - эпюра оползневого давления
Затем, идя сверху вниз от отсека 1, рассматривается последовательно равновесие каждого отсека, при этом берется сумма проекций всех сил на направление возможного смещения. Первоначально было принято в данном способе определять сумму проекций всех сил на горизонталь или на некоторое общее направление смещения. Однако при решении задачи в проекциях на это направление получались неизвестными реакции со стороны несмещаемого основания. В связи с этим в этом методе стали рассматриваться условия равновесия относительно направления возможного скольжения внутри каждого отсека и потому получаются проекции оползневого давления всей вышележащей части оползня, включая и рассматриваемый отсек, на направление скольжения в этом отсеке.
Задача решается, как указывалось, последовательно по отсекам. Так, для отсека 1 берется сумма проекций всех сил на направление a - b . Отсюда определяется величина реакции E 1 , которая должна быть приложена к отсеку 1 со стороны отсека 2 на направлении a - b для обеспечения равновесия отсека 1. Величина этой реакции равна давлению, передаваемому от первого отсека второму. Аналогично рассматривается равновесие 2-го, 3-го и т.д. отсеков в проекциях на соответствующие направления с учетом соответствующих давлений E 1 , E 2 , E 3 и т.д. от вышележащих отсеков. Таким образом определяется оползневое давление в конце каждого отсека от головы (вершины) до подошвы оползня ( E оп ).
Для наглядного представления об изменении оползневого давления по длине оползня и для нахождения давления в интервалах между границами отсеков здесь же, под разрезом по оползню, строится эпюра оползневого давления (см. рис. 18). Этой эпюрой можно также пользоваться, как будет показано ниже, для выбора места заложения сооружения по длине оползня.
Когда выбрано место заложения удерживающего сооружения и определена соответствующая этому месту величина оползневого давления, последнее, по Л.П. Ясюнас, затем увеличивается в K у раз, где K у - заданный коэффициент устойчивости, и на величину этого давления производится расчет удерживающей конструкции. Однако, как вытекает из работы [ 6], умножение на Kу величины результирующей силы (вместо суммарной величины сдвигающих сил) значительно снижает расчетную величину оползневого давления. По выполненному нами анализу при небольшой разнице между сдвигающими и удерживающими силами (до 20 %) оползневое давление может быть занижено в 6 - 7 раз. Поэтому такое использование коэффициента устойчивости следует считать неправильным. Это видно и из следующих соотношений:
K у = Ri / Qi ; E оп = K у Qi - Ri . ( 103)
Для упрощения вычислений Л.П. Ясюнас использует понятие единичного оползневого давления. Из рисунка 18, а, проектируя все силы на направление поверхности скольжения, получаем величину единичного оползневого давления от грунтового массива длиной, шириной и толщиной, равными единице:
e оп. i = γisin αi - γicos αitg φi - ![]() = ( γi / cos φi )( sin αicos φi - cos αisin φi ) -
= ( γi / cos φi )( sin αicos φi - cos αisin φi ) - ![]() ,
,
откуда
e оп. i = ( γi / cos φi ) sin ( αi - φi ) - ![]() . ( 104)
. ( 104)
Вычитаемое в написанном выражении получено из следующих соображений. Полное сцепление по подошве i -го отсека равно cili . Для получения сцепления по подошве единичного объема полное сцепление необходимо разделить на объем отсека:
![]()
Оползневое давление от одного отсека равно:
Ei = Pi sin αi - Pi cos αitg φi - cili = γiaih ср . i sin αi - γiaih ср . i cos αitg φi - cili =
[ γisin αi - γicos αitg φi - cili / aih ср . i ] aih ср . i = [( γi / cos φi ) sin ( αi - φi ) - ci / h ср . i cos αi ] aih ср . i . ( 105)
Как показано выше, выражение в квадратных скобках есть e оп. i , следовательно
Ei = e оп i aih ср . i . ( 106)
Определение оползневого давления рассматриваемым методом может выполняться двумя способами. По первому из них оползневое давление от одного отсека выражается через его вес
Ei = (Pi/cos φi)sin(αi - φ i ) - ciai/cos αi . ( 107-а)
Или с учетом коэффициента устойчивости, сейсмического воздействия и гидродинамической силы
Ei = K у [( P в i / cos φi ) sin ( αi - φ i ) + Qci + ji - c в i ai / cos αi ]. ( 107-б)
Как только что было показано, не строго в этой формуле то, что на коэффициент устойчивости умножены и сдвигающие и удерживающие гравитационные силы. Однако мы оставляем для анализа формулу в таком виде, в каком ее использовал автор.
Полное оползневое давление в конце каждого отсека складывается из оползневого давления от данного i - го отсека плюс проекция на направление поверхности скольжения в этом отсеке усилия от всей вышележащей части оползня:
E оп .i = Ei + E оп .(i-1) cos |αi -1 - αi|. ( 108)
Направление действия этого оползневого давления параллельно поверхности скольжения в i -ом отсеке.
По второму способу используется единичное оползневое давление. Из рассмотрения выражения e оп. i следует, что:
единичное оползневое давление не зависит от длины оползня;
ввиду наличия в оползневом грунте на поверхности скольжения сцепления единичное давление зависит от мощности оползающих масс; с увеличением мощности оползающих масс h ср. i влияние сцепления уменьшается;
при углах наклона плоскостей скольжения, равных углам трения грунта по этим плоскостям ( α = φ), даже при неучете влияния сцепления ( c = 0), единичное оползневое давление равно нулю, при учете же сцепления давление отрицательно, т.е. имеется некоторый «запас» сил сопротивления сдвигу. Учет этого обстоятельства имеет большое значение при проектировании удерживающих сооружений и планировочных работ на оползнях;
для случаев, когда единичное оползневое давление отрицательно, дополнительная нагрузка на склоне не приведет к нарушению его равновесия.
Оползневое давление от каждого отсека определится по формуле (при наличии гидродинамической силы и сейсмического воздействия)
Ei = Kу( e оп. i a i h ср. i + Q сi + ji ). ( 109)
При учете гидродинамического давления (фильтрационной силы), создаваемого сплошным потоком грунтовых вод, объемный вес грунта следует принимать взвешенным в воде. При струйчатых потоках грунтовых вод объемный вес грунта следует принимать в естественном состоянии. При отсутствии грунтовых вод в написанной формуле принимают ji = 0. При расположении склона в несейсмическом районе - Q сi = 0. K у в формуле ( 109) также оставлено, как у Л.П. Ясюнас, множителем ко всему выражению. Полное оползневое давление в конце каждого отсека, как и ранее, равно:
E оп .i = Ei + E оп .(i-1) cos |αi-1 - αi|.
Таким образом, последовательно добавляя (начиная от верхнего отсека) к E оп. i значения проекций на соответствующие направления всех E оп.( i -1) , определяется ΣE оп , т.е. значение оползневого давления в конце соответствующего i - го отсека от всей вышележащей части оползня на направлении поверхности скольжения в данном отсеке. Затем, как было показано выше, строится эпюра оползневого давления.
Единичное оползневое давление e оп. i = ( γi / cos φi ) sin ( αi - φi ) - ci /( h ср. i cos α ) Л.П. Ясюнас предлагает определять с помощью графиков зависимостей каждого из членов данного уравнения:
уменьшаемого - от φi при различных значениях αi (для каждого конкретного значения γi );
вычитаемого - от ci при различных значениях h ср. i ( cos αi в формуле Л.П. Ясюнас отсутствовал, так как h ср. i принималось перпендикулярно поверхности скольжения).
Поскольку первая зависимость строится для конкретного объемного веса грунта γ i , то такие графики удобны лишь для склона, сложенного полностью однородным грунтом. В противном случае необходимо для каждого отсека строить свои зависимости, что нерационально.
Общие графики для различных практических случаев автором не были построены.
2.13 . Метод ДИИТа
Данный метод разработан на кафедре оснований и фундаментов Днепропетровского института инженеров транспорта авторами Б.В. Веселовским, А.Г. Дорфманом, Д.В. Смирновым и М.И. Шевченко под руководством д-ра т. н. М.Н. Гольдштейна [ 1, 9].
Метод дает возможность рассчитывать оползневое давление и устойчивость склона против переползания грунта через удерживающую конструкцию (общий коэффициент устойчивости склона этим методом не вычисляется).
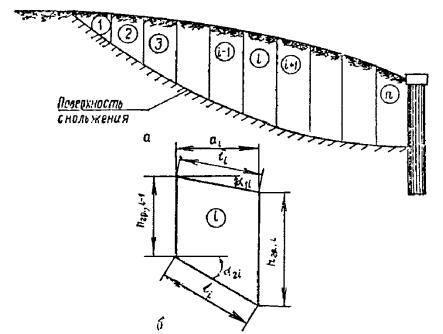
Рис. 19 . Метод ДИИТа:
а - оползневой склон; б - схема i -го отсека
Для определения оползневого давления и точки приложения оползневой силы весь массив грунта, ограниченный свободной поверхностью сверху и поверхностью скольжения снизу (которая предполагается известной), разбивается на отсеки (рис. 19, а). При этом считается, что грунт вдоль поверхности скольжения находится в предельном состоянии.
В соответствии с обозначениями, приведенными на рис. 19, б , размеры i -го отсека таковы:
h гр .,i = hh гр .,i-1 - aitg α1i + aitg α2i = h гр .,i-1 + ai(tg α2i - tg α1i); ( 110)
![]()
![]()
![]()
![]() = h гр .,i-1 + (ai /2)(tg α2i - tg α1i) = h гр .,i - ai(tg
α2i - tg α1i) + (ai /2)(tg
α2i - tg α1i) =
= h гр .,i-1 + (ai /2)(tg α2i - tg α1i) = h гр .,i - ai(tg
α2i - tg α1i) + (ai /2)(tg
α2i - tg α1i) = ![]() - (ai /2)(tg α2i
- tg α1i).
- (ai /2)(tg α2i
- tg α1i).
h гр., i ; h гр., i -1 - граничные вертикальные размеры отсека. Вес отсека равен:
![]() ( 111)
( 111)
Силы, действующие на отсек, показаны на рис. 20, а . Сцепление заменено сжимающим напряжением
![]() ( 112)
( 112)
Подобно тому, как это делалось в методе Р.Р. Чугаева, принимается, что реакции по боковым граням отсека отклоняются от нормали на угол φ/2. По условиям равновесия силовой многоугольник замкнут (см. рис. 20, б).
Рассматривая треугольники, находим:
СВ = ![]() KC =
KC = ![]() aitg
α2i; BK =
aitg
α2i; BK = ![]() ai ;
ai ;
Ð CAK = arctg ![]() ( 113)
( 113)
N' пр = AC = ![]()
β 1 = Ð DAC = α2i -
φ - arctg ![]() ( 114)
( 114)
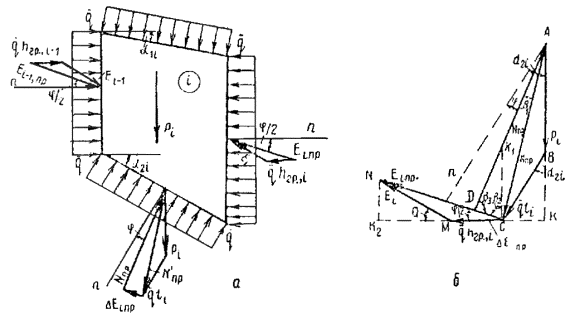
Рис. 20 . Схемы сил:
а - силы, действующие на отсек; б - силовой многоугольник
β2 = Ð DCA = π /2
- φ /2
+ arctg ![]()
β3 = Ð ADC = π - β 1 - β 2 = π /2 + 3 φ /2 - α 2 i ; ( 115)
![]()
![]() ( 116)
( 116)
Ei пр = Ei -1, пр + ΔEi пр ; Ei пр = ![]() ( 117)
( 117)
NK 2 = Ei пр sin ( φ /2);
CK 2 = Ei пр cos ( φ /2);
K 2 M = Ei пр cos ( φ /2)
- ![]() h гр., i ;
h гр., i ;
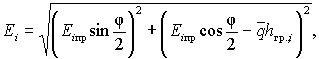 ( 118)
( 118)
где E iпр - приведенное боковое давление;
Ei - равнодействующая оползневого давления.
Угол наклона равнодействующей к горизонтали определяется по формуле
θ = Ð NMK 2 = 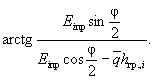 ( 119 )
( 119 )
Расстояние Д1А от нижней точки отсека до точки приложения силы Ei равно zi (рис. 21, б). Для первого отсека из рис. 21, а имеем:
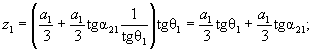
z 1 = (a1/3)(tg θ1 + tg α21). ( 120)
Для всех остальных отсеков zi определяется следующим образом.
Координата АД точки приложения равнодействующей оползневого давления определяется из условия равенства нулю моментов сил Ei и Ei -1 относительно точки О i . Плечи сил Ei и Ei -1 обозначим соответственно через Li и Li -1 . Условие равновесия запишется в виде
Ei -1 Li -1 + EiLi = 0. ( 121)
Расчет ведется последовательно от первого до последнего отсека. Для i -го отсека имеем:
L i -1 = Oi C'i; Li = Oi Ci .
Из расчета i - 1-го отсека известны плечи приложения силы Ei -1 : L ' i -1 = O i -1 C ' i -1 и zi -1 = A 1 F .
Из рис. 21, б имеем:
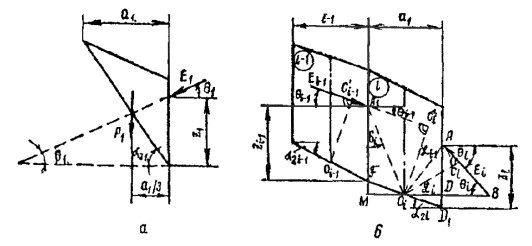
Рис. 21 . Определение точки приложения силы Ei :
а - для первого отсека; б - для i -го отсека
FM = (ai/2)tg α2i; A 1M = zi-1 + (ai/2)tg α2i. ( 122)
Для определения плеча Li соединяются точки приложения Ei -1 и Ei с точкой Оi отрезками А1О i и АОi; из точки Оi проводится горизонтальная линия до пересечения с линией действия силы Ei . Из полученных треугольников находятся:
δ i = Ð MA1Oi = arctg ![]()
A1Oi = ai/2 sin δi Ð OiA1C'i = π/2 - θi-1 - δi;
sin Ð OiA1C'i = cos(θi-1 + δi);
L i -1 = OiC'i (ai/2 sin δi ) cos(θi-1 + δi); Li = (Ei-1/Ei )Li-1;
L i = (Ei-1/E i ) × (ai/2 sin δi ) × cos(θi-1 + δi);
Ð ABO i = θi; OiB = Li/sin θi; ДВ = Li/sin θi - ai/2;
АД = ( Li /sin θi - ai/2)tgθi . ( 123)
АД - ордината точки приложения оползневого давления. Расстояние zi от нижней точки отсека до точки приложения силы E i выражается окончательно формулой
zi = ( Li / sin θi - a i /2) tgθi + ( a i /2) tg α 2 i . ( 124)
Таким образом, полностью определена по величине, направлению и точке приложения равнодействующая оползневого давления.
Для определения возможности переползания грунта через удерживающую конструкцию рассматриваются несколько призм выпора и для каждой находится требуемое давление E тр (критическая сила, сопротивляющаяся выпору, или сила выпора), которое затем сравнивается с оползневым давлением E оп . Если E тр > E оп - выпора нет, если E тр ≤ E оп - происходит выпор грунта и переползание его через удерживающую конструкцию. Предполагается, что линия выпора - прямая, и, начиная с отсеков, примыкающих к удерживающей конструкции, намечается несколько призм выпора. Согласно рис. 22, а определяются геометрические размеры и вес клина выпирания (на рисунке заштрихован). При этом размеры граничных сторон каждого отсека, в зависимости от его месторасположения, определяются по одной из следующих формул:
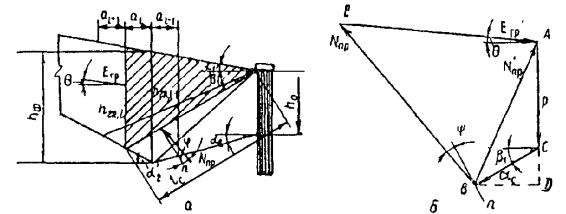
Рис. 22 . Определение силы выпора:
а - схема клина выпирания; б - силовой многоугольник
h гр .,i-1 = (h о + (tg α 1 + tg α 2 ) ![]() ; ( 125)
; ( 125)
h гр .,i = (h ф + (tg α 1 + tg α 2 ') ![]() , ( 126)
, ( 126)
где h о - высота грани отсека, примыкающей к удерживающей конструкции;
h ф - высота отсека в точке излома поверхности скольжения.
Вес клина ![]() , параметры линии выпора:
, параметры линии выпора:
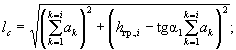
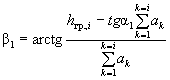 ( 127 )
( 127 )
На рис. 22, б построен силовой многоугольник, в котором АС = Р ; BC = C = cl с = q (сцепление грунта по поверхности выпирания); AB = N ' пр - равнодействующая веса и сцепления; BE = N пр - реакция неподвижного массива грунта; AE = E тр - требуемое давление. Реакция N пр отклоняется от нормали к плоскости сдвига на угол внутреннего трения грунта φ . Сила, необходимая для того, чтобы произошел выпор, E тр отклоняется от горизонтали на угол θ (способ его определения изложен выше). Дополнительно проводится отрезок ДВ ^ АС . Из рассмотрения полученных треугольников вытекает:
СД = q sin β 1 ; ДВ = q cos β 1 ; АД = P + q sin β 1 ;
N ' пр = ![]() Ð Д AB =
Ð Д AB =
![]() ;
;
Ð ACB = π /2 + β 1 ; Ð ABC = π /2 - ( β 1 + ![]() );
);
Ð CBE
= π/2 + φ; Ð BAE = π/2 + θ - ![]() ;
;
Ð ABE = π/2 - Ð ABC + φ = φ + β1 + ![]() ;
;
Ð AEB = π - Ð BAE - Ð ABE = π -
π/2 - θ + ![]() - φ - β1
-
- φ - β1
- ![]() = π/2 - θ -
φ - β1.
= π/2 - θ -
φ - β1.
По теореме синусов ![]() , откуда сила выпора вычисляется по формуле
, откуда сила выпора вычисляется по формуле
![]() ( 128 )
( 128 )
Данный аналитический метод определения оползневого давления может быть применен к расчетам оползневых склонов, имеющих различные рельеф и форму поверхности смещения, любое геологическое строение. При этом в расчет вводятся характеристики грунта, полученные с учетом увлажнения оползневых склонов и изменения их в результате сезонных колебаний климатических факторов. Ввиду того, что выведенные формулы достаточно просты, программирование расчета не вызывает особых затруднений. Программа вычислений состоит из операций последовательного определения всех параметров, участвующих в расчете.
Авторы данного метода не привели способа учета сейсмической и гидродинамической сил. Мы при вычислении настоящим методом оползневого давления в сейсмических районах и при наличии потока грунтовых вод будем, с некоторым приближением, пользоваться формулой для расчета приведенного бокового давления в каждом отсеке:
![]() ( 129 )
( 129 )
где Q ск и j к - соответственно сейсмическая и гидродинамическая силы в каждом отсеке, определяемые способами, изложенными в предыдущих методах расчета.
Авторы не привели стройного алгоритма для вычисления оползневого давления вручную. Это не дает возможности использовать данный метод при оперативных расчетах без применения ЭВМ.
К недостаткам метода следует отнести и отсутствие способа учета требуемого коэффициента устойчивости при вычислении расчетной величины оползневого давления (так как сдвигающие и удерживающие силы здесь не разделяются). Как было показано ранее, умножение на K у получаемой величины E оп является неправильным. Однако в вычислениях, которые нами будут выполняться для сравнения рассматриваемых методов, мы, за неимением иного способа, будем определять расчетное оползневое давление по формуле
E оп р = K у E оп . ( 130)
В целом же метод может быть опробован для расчета противооползневых удерживающих конструкций, хотя он и весьма сложен.
2.14 . Определение давления от призмы обрушения по теории Кулона
Как известно, в строительной механике давление на подпорную стену от ограждаемого ею грунта принято, основываясь на гипотезе Кулона, определять как активное давление сыпучего тела. Предполагается некоторая; весьма незначительная подвижка стены от массива, которая вызовет отделение от сыпучего тела некоторой призмы грунта. При этом предполагается, что сдвиг происходит по плоскости и сыпучее тело в объеме упомянутой призмы сдвигается, приняв форму затвердевшего клина. Давление E а , производимое сыпучим телом на смещающуюся стенку, то есть давление от этого затвердевшего клина, называется активным давлением грунта. На это давление E а обычно и рассчитываются подпорные стены, устои мостов, набережные и т.д. Наоборот, при надвижке подпорной стены на грунт (например, в уровне заделки стены ниже дневной поверхности) возникает так называемое пассивное давление грунта E п . В частном случае, при горизонтальной поверхности сыпучего тела (грунта), вертикальной задней грани подпорной стены и отсутствии сцепления, эти давления, как известно, равны:
E а = (1/2) γH 2 tg 2 (45° - φ /2); E п = (1/2) γH 2 tg 2 (45° + φ /2). ( 131)
При связном грунте (наличии сцепления) эти результирующие давления выражаются формулами:
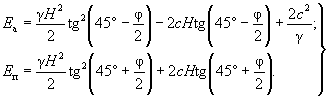 ( 132)
( 132)
Практика показала, что несмотря на ряд допущений, расчет на активное давление грунта в большинстве случаев дает достаточно надежные подпорные стены.
Однако так решается задача в обычных (неоползневых) условиях.
В практике проектирования удерживающих конструкций или подпорных стен на оползнях также нередко при определении давления на такое сооружение от оползня совершенно безосновательно пользуются приведенной выше формулой активного давления сыпучего тела, не имеющего ничего общего с действительным давлением на конструкцию в таких случаях. Такое определение оползневого давления для расчета противооползневых сооружений является глубоко ошибочным и вытекает из неправильного представ ления о сущности активного давления и давления от оползня на устраиваемую на нем удерживающую конструкцию.
Оползневое давление определяется из рассмотрения условий равновесия всего оползневого массива, а не части его, в том числе в виде клина, который, как легко понять, на оползне (неустойчивом и требующем удержания) не может иметь значения. Здесь должна предполагаться некоторая микроподвижка удерживающей конструкции, при которой произойдет смещение, но не части массива в виде клина, а всех оползневых масс. В таком случае для обеспечения устойчивого состояния оползня устройством удерживающей конструкции последняя должна дать в сторону, обратную движению оползня, реакцию, равную разности между активными (сдвигающими) и реактивными (сопротивляющимися сдвигу или удерживающими) силами по всей поверхности смещения оползня. Такая конструкция приведет оползень в состояние равновесия. На величину силы оползневого давления, равной этой потребной реакции, с учетом необходимого коэффициента запаса (или требуемого коэффициента устойчивости) и должна быть рассчитана противооползневая удерживающая конструкция.
Активное давление грунта по теории Кулона и оползневое давление от неустойчивого грунтового массива - величины совершенно различные и их не следует смешивать. Численно они могут совпадать, как мы увидим в дальнейшем, лишь в тех случаях, когда по закономерностям оползневых процессов рассчитывается вертикальный откос с горизонтальными (верхней и нижней) поверхностями грунта, при однородном сложении склона, без участия гидродинамических и сейсмических сил. Причем в грунтовом массиве при этом не должно быть никакой иной ослабленной поверхности скольжения, кроме получающейся по теории Кулона.
Кстати, совершенно непонятно, по каким соображениям проектировщики определяют оползневое давление именно как активное. Поскольку весь грунт надвигается на удерживающую конструкцию (что аналогично надвижке конструкции на грунт), то логичней уж было бы определять его как пассивное, хотя, разумеется, и оно не имеет ничего общего с оползневым давлением.
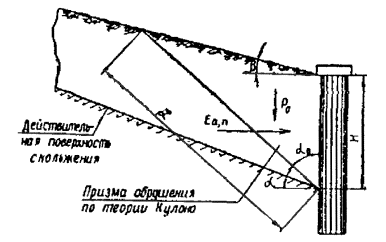
Рис. 23 . Методы, основанные на теории Кулона
Чтобы в дальнейшем у проектировщиков не возникало искушения применять гипотезу Кулона для определения оползневого давления, мы введем в общее численное сравнение рассматриваемых методов и давления, определенные, как активное и пассивное по Кулону. Повторяем - делается это только для того, чтобы выявить, насколько велика разница между этими способами расчета и методами определения истинного оползневого давления.
Формулы для определения активного и пассивного давления связного грунта при наклонной его поверхности (рис. 23) и принятии угла трения об удерживающую конструкцию равным нулю возьмем без выводов из нормативной литературы [ 21]:
![]() ( 133 )
( 133 )
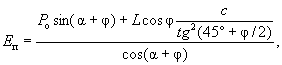 ( 134)
( 134)
где P о - вес призмы выпора;
L - длина плоскости выпора грунта.
Величины E а и E п по написанным формулам определяются подбором для нескольких величин углов α 0 и α . За расчетное принимается наибольшее из вычисленных таким образом значений E а или E п . При этом при определении активного давления расчеты методом подбора рекомендуется начинать с угла α 0 = 45° - φ /2, а при определении пассивного давления - с угла α = 45° - φ /2 (углы наклона плоскости скольжения по теории Кулона при горизонтальной поверхности грунта).
При наличии водонасыщения грунта физико-механические характеристики принимаются для грунта в замоченном состоянии. При наличии интенсивного потока грунтовых вод к значениям E а или E п следует добавлять величину гидродинамической силы, определенной приведенными выше методами. Также необходимо поступать и с сейсмической силой при рассмотрении склонов в сейсмических районах. Кроме того, допускается увеличенное значение давления грунта от землетрясения определять по формуле [ 11 , 16]
q а,п = (1 + 2 μtg φ ) E а,п , ( 135)
где q а,п - соответственно активное или пассивное давление грунта;
μ - коэффициент сейсмичности;
E а,п - активное или пассивное давление грунта без учета сейсмичности.
III . АНАЛИЗ И ВЫВОДЫ
3.1 . Сравнение методов расчета
Для численного сравнения применяемых методов расчета определялись фактические коэффициенты устойчивости и оползневые давления для пяти реальных склонов. Большой объем вычислительной работы был проделан с помощью ЭВМ «Минск-22М». На основании этих вычислений для всех склонов построены эпюры оползневого давления (рис. 24 - 28), которые и рассматривались при анализе методов расчета.
По эпюрам определялись величины оползневого давления для сечений I - I , в которых проектировались противооползневые удерживающие конструкции глубокого заложения. Эти величины, так же как и значения фактических коэффициентов устойчивости каждого склона, приведены в табл. 6.
На рисунках и в табл. 6 конкретные оползневые склоны обозначены условными шифрами. В разрезе склона построены две поверхности скольжения: сплошной линией - первоначально намечавшаяся по материалам инженерно-геологических изысканий, пунктирной - расчетная (экстремаль), полученная в результате вариационных расчетов.
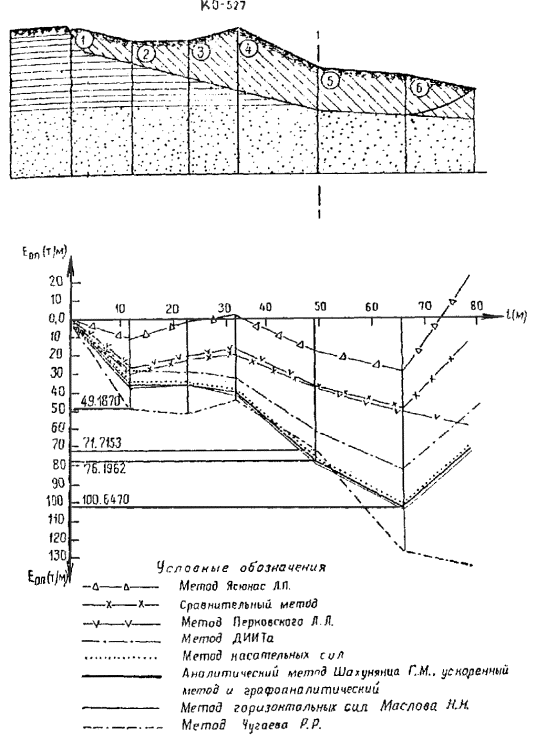
Рис. 24 . Сравнение эпюр оползневого давления, рассчитанного различными методами
К сожалению, в натурных условиях действительные максимальные оползневые давления практически определить не удается из-за несовершенства измерительных приборов, сложности установления момента появления предельного (критического) состояния в склоне и т.д. Все же в одном из склонов (КТ-1859) автору удалось замерить оползневое давление косвенным путем - с помощью измерения напряжений в тензосваях, оставленных в грунтовом массиве на длительный срок. Как видно из табл. 6, величина этого давления приближалась к значениям, определенным методами Н.Н. Маслова и Г.М. Шахунянца. Если учесть, что момент предельного состояния в склоне мог быть еще не достигнут и фактические давления со временем окажутся больше замеренных, то следует считать результаты, полученные методами Н.Н. Маслова (горизонтальных сил) и Г.М. Шахунянца, наиболее близкими к действительным.
В остальных случаях анализ методов расчета производился, исходя из реального состояния склонов. Например, по их оползневым подвижкам ориентировочно устанавливался коэффициент устойчивости, который сравнивался с величинами, определенными различными методами. При наличии оползневых подвижек и явной фактической неустойчивости склонов (или состояния, близкого к предельному) неприемлемым считался метод, который давал отрицательные величины оползневых давлений.
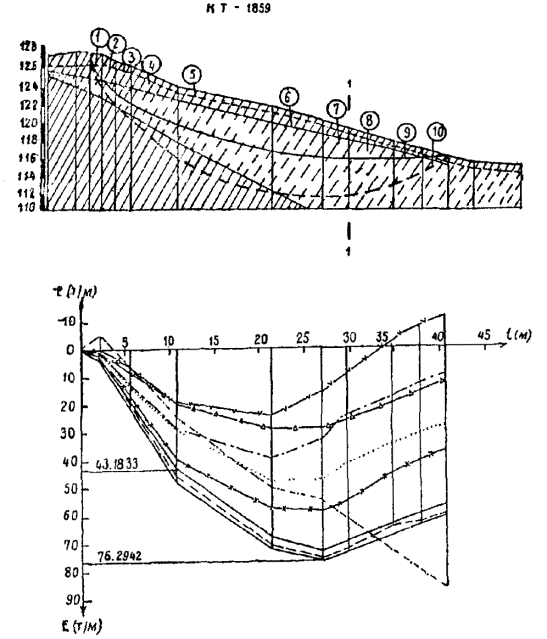
Рис. 25 . Продолжение сравнения
Важным фактором при анализе методов расчета являлась и абсолютная величина получаемых оползневых давлений. Ясно, что при прочих равных условиях предпочтение должно отдаваться тем методам, которые дают большие величины. Тогда любая имеющаяся неточность в исходных положениях в процессе выполнения расчетов пойдет в запас.
Кроме того, учитывались общие расчетные предпосылки, положенные в основу каждого метода (удовлетворение трем уравнениям статики, учет взаимодействия отсеков, правильное введение заданного коэффициента устойчивости и т.д.). Например, для сравнения способов учета заданного коэффициента устойчивости в общий анализ был введен так называемый сравнительный метод расчета, в котором на величину K у умножалась результирующая величина давления, а не сдвигающие силы. Проверка на многих склонах показала неверность такого способа учета K у .
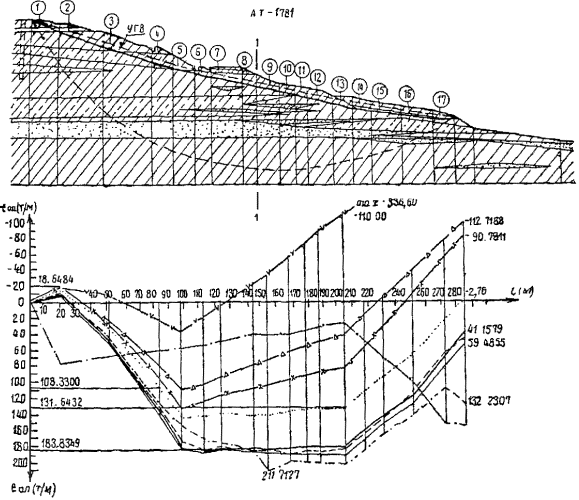
Рис. 26 . Продолжение сравнения
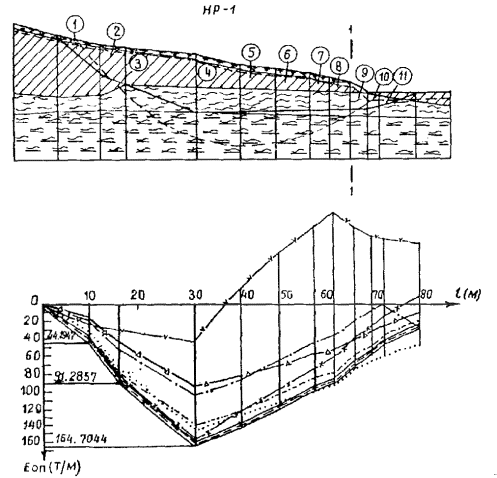
Рис. 27 . Продолжение сравнения
Анализировались и формы эпюр оползневого давления, приведенных на рис. 24 - 28. Ясно, что линия эпюры, как правило, должна, во-первых, быть относительно плавной, во-вторых, возрастать по направлению от бровки склона к его подошве, в-третьих, не переходить через нулевую линию в случае, когда склон находится в состоянии, близком к предельному.
Таблица 6
Сравнение методов расчета устойчивости склонов и величины оползневого давления
|
Шифр склона |
Рассчитываемая величина |
Метод определения |
|||||||||||||
|
Круглоцилиндрической поверхности скольжения |
Ю.И. Соловьева |
Р.Р. Чугаева |
Горизонтальных сил Н.Н. Маслова |
Касательных сил |
Аналитический Г.М. Шахунянца |
Графоаналитический Г.М. Шахунянца |
Ускоренный Г.М. Шахунянца |
Графостатический Л.П. Перковского |
Блока и призм Б.К. Хоу |
Л.П. Ясюнас |
ДИИТа |
Давление от призмы обрушения по Кулону E а / E п |
Ориентировочные величины по результатам натурного определения |
||
|
КТ-1859 |
K у |
0,766 |
0,846 |
0,466 |
0,786 |
0,889 |
0,736 |
- |
0,736 |
- |
- |
- |
- |
- |
0,7 ¸ 0,8 |
|
E оп |
- |
- |
50,7 |
69,4 |
49,2 |
73,2 |
72,6 |
73,2 |
25,0 |
80,0 |
29,7 |
40,7 |
15,9/43,5 |
58,3 |
|
|
НР-1 |
K у |
0,898 |
0,862 |
0,766 |
1,045 |
0,919 |
1,027 |
- |
1,027 |
- |
- |
- |
- |
- |
1,00 |
|
E оп |
- |
- |
58,3 |
67,2 |
76,7 |
70,2 |
70,0 |
70,2 |
-90,0 |
-60,0 |
41,1 |
48,9 |
32,0/66,5 |
- |
|
|
АТ-1781 |
K у |
0,635 |
1,126 |
1,000 |
1,054 |
1,103 |
1,067 |
- |
1,067 |
- |
- |
- |
- |
- |
1,00 |
|
E оп |
- |
- |
211,7 |
191,2 |
142,1 |
184,8 |
184,8 |
184,8 |
-31,0 |
- |
74,8 |
- |
28,0/55,0 |
- |
|
|
КО-527 |
K у |
0,799 |
0,998 |
1,150 |
0,979 |
1,007 |
1,014 |
- |
1,014 |
- |
- |
- |
- |
- |
1,02 |
|
E оп |
- |
- |
71,7 |
77,2 |
75,4 |
76,2 |
76,2 |
76,2 |
37,5 |
- |
17,9 |
60,0 |
93/196 |
- |
|
|
НР-2 |
K у |
0,983 |
1,037 |
1,110 |
1,172 |
1,099 |
1,154 |
- |
1,154 |
- |
- |
- |
- |
- |
1,00 |
|
E оп |
- |
- |
52,9 |
69,2 |
86,5 |
70,7 |
70,7 |
70,7 |
-70,1 |
-60,0 |
6,8 |
52,6 |
25,0/72,5 |
- |
|
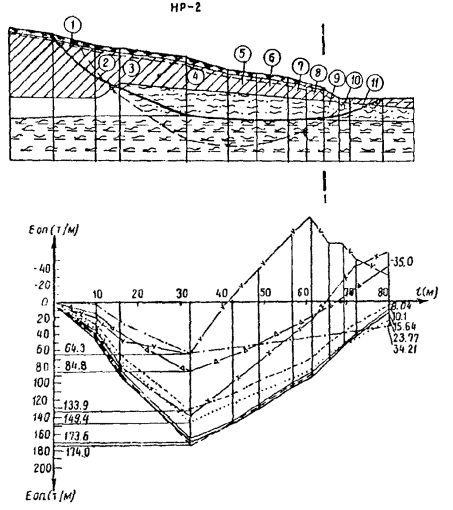
Рис. 28 . Продолжение сравнения
3.2 . Рекомендации по применению
На основе проведенного анализа сделаны следующие выводы. Для проектирования противооползневых удерживающих конструкций глубокого заложения наиболее приемлемыми являются методы Н.Н. Маслова и Г.М. Шахунянца. Причем при выполнении расчетов на ЭВМ следует применять метод горизонтальных сил Н.Н. Маслова или аналитический Г.М. Шахунянца. При расчетах вручную рекомендуется использовать разработанный автором ускоренный способ определения оползневого давления методом Г.М. Шахунянца.
Достоверность принятой методики проверена более чем на 60 противооползневых удерживающих конструкциях, запроектированных и построенных за последние 12 лет. Статистическая обработка результатов расчетов, а также наблюдения за поведением эксплуатируемых сооружений подтвердили, что методы Шахунянца и Маслова дают наиболее близко отвечающие действительным величины оползневого давления. В Укрспецстройпроекте разработаны программы для выполнения этих расчетов на ЭВМ.
Наиболее опасная поверхность скольжения (экстремаль) может быть установлена методом пробных попыток - путем расчета коэффициентов устойчивости склона для различных поверхностей и принятия той, для которой Kу минимален.
Когда поверхность скольжения не предопределена геологическим строением склона и наиболее опасное ее положение нельзя установить по материалам инженерно-геологических изысканий, оползневое давление можно определять вариационными методами расчета, которые в настоящей работе из-за ограниченности места не рассматриваются.
Для определения коэффициента устойчивости склона, кроме методов Г.М. Шахунянца и Н.Н. Маслова, допускается применять методы круглоцилиндрической поверхности скольжения (как правило, в однородных грунтах) и Ю.И. Соловьева.
3.3 . Принципы построения эпюры оползневого давления
В связи с освоением территорий, которые раньше считались непригодными, в последнее время все шире выполняются специальные монтажные работы, связанные с укреплением оползневых склонов.
Для расчета противооползневых сооружений и проверки устойчивости склона до его укрепления и после требуется по каждому из расчетных поперечников, как это указывалось выше, построить эпюру оползневого давления E оп (рис. 29). Построение этой эпюры должно производиться с одновременным уточнением сдвиговых (или прочностных) характеристик грунта в уровне поверхности скольжения (угла внутреннего трения φ и удельного сцепления c ), причем положение самой поверхности скольжения также уточняется методом подбора. Вычисление значений оползневого давления в каждом отсеке, на которые условно разбивается оползневой склон, производится по формулам, в которые, как мы видели ранее, непосредственно входят величины прочностных характеристик грунтов. В связи с этим порядок уточнения характеристик и положения поверхности скольжения, а также выполнение всех прочих расчетов имеет важное значение. Ниже излагается последовательность проведения вычислений, установленная на основе большого опыта проектирования противооползневых сооружений и наблюдения за поведением укрепленных склонов.
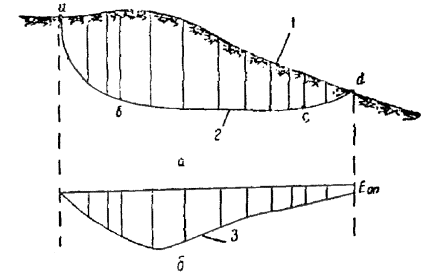
Рис. 29 . Расчетный поперечник (а) с эпюрой оползневого давления (б):
1 - поверхность склона; 2 - поверхность скольжения; 3 - контур эпюры оползневого давления
Положение поверхности скольжения, также как и значения прочностных характеристик грунтов (φ и c ), установленные по материалам инженерно-геологических изысканий, следует при практическом проектировании уточнять обратными расчетами, исходя из значения коэффициента устойчивости склона, приблизительно соответствующего его значению при фактическом состоянии склона. При этом используются известные из вышеприведенного соотношения:
K у = Σ R уд / ΣQ сдв ; ( 136)
E оп = K у з ΣQ сдв - Σ R уд , ( 137)
K у - задаваемый коэффициент устойчивости;
K у з - задаваемый коэффициент устойчивости;
Σ R уд - сумма удерживающих сил вдоль по склону (в расчетном поперечнике);
ΣQ сдв - сумма сдвигающих сил.
На практике могут встречаться следующие варианты расчетов.
1- й случай - склон неустойчив (проявляются четкие оползневые подвижки). При этом по фактически установленным в процессе инженерно-геологических изысканий поверхности скольжения и прочностным характеристикам грунтов по расчету получается, что Kу ≤ 1, т.е. расчеты соответствуют фактическому состоянию склона. В таком случае принимаются для расчета оползневого давления прочностные характеристики грунтов, определенные по материалам инженерно-геологических изысканий (при сдвиге образцов в естественном состоянии, отобранных на уровне предполагаемой поверхности скольжения): φ = φфакт; c = c факт , а положение наиболее опасной поверхности скольжения уточняется по этим характеристикам методом подбора (этот метод будет описан ниже), поскольку определенная изысканиями поверхность скольжения может быть не самой опасной. Эпюра оползневого давления строится для наиболее опасной поверхности скольжения по прочностным характеристикам φ = φфакт; c = c факт .
2- й случай - склон неустойчив, однако по установленным в процессе изысканий поверхности скольжения и прочностным характеристикам грунтов в естественном состоянии (φфакт, c факт ) получается Kу > 1. Это говорит о том, что в процессе инженерно-геологических изысканий какие-то параметры установлены не достоверно и требуют уточнения обратными расчетами, исходя из условия Kу ≈ 1, ибо это условие означает состояние предельного равновесия. В таком случае уточнение положения поверхности скольжения методом подбора и прочностных характеристик грунтов производится следующим образом.
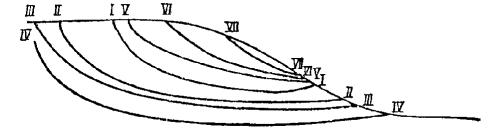
Рис. 30 . Нахождение экстремальной поверхности скольжения:
I - поверхность скольжения, найденная в процессе инженерно-геологических изысканий; II - VII - поверхности скольжения, намечаемые в процессе нахождения экстремали методом подбора
Сначала по установленным фактическим (для естественного состояния грунтов) прочностным характеристикам φфакт и c факт осуществляется поиск наиболее опасной поверхности скольжения. С этой целью строят целый ряд возможных поверхностей скольжения (рис. 30), которые намечают исходя, во-первых, из реального сложения склона (учитываются закольные трещины, имеющиеся ослабленные поверхности, участки возможного скольжения слоя по слою и т.д.), во-вторых, из получения диапазона величин коэффициента устойчивости с уменьшением и увеличением его при движении с возможными поверхностями в обе стороны от первоначально намеченной при геологических изысканиях. Если обратиться к рис. 30, то надо найти такие формы поверхностей скольжения, чтобы, например, выполнялись соотношения: K IV > K III < K II < K I ; K I > K V > K VI < K VII , где K I , K II , K III - коэффициенты устойчивости склона для соответствующих поверхностей скольжения. После нахождения семейства таких кривых для дальнейших расчетов оставляется та поверхность скольжения, для которой коэффициент устойчивости склона минимален ( K у min ). Такая поверхность скольжения склона называется экстремальной. Для этой поверхности скольжения, принимая для нее Kу ≈ 1, обратными расчетами уточняют значения φ и c . При этом прочностные характеристики подбираются в диапазоне:
 ( 138)
( 138)
где φ min , c min - минимальные прочностные характеристики грунтов в уровне поверхности скольжения, определенные по образцам грунтов в лаборатории при испытании на сдвиг, как правило, по схеме «плашка по плашке» по смоченной поверхности;
φ , c - прочностные характеристики грунтов, принимаемые для дальнейших вычислений (уточняются с помощью обратных расчетов);
φ факт , c факт - прочностные характеристики грунтов в естественном состоянии (определяются лабораторными или натурными методами).
Затем по найденным величинам φ и c для экстремальной поверхности скольжения определяются значения оползневого давления в каждом отсеке расчетного поперечника и под ним по этим значениям строится эпюра оползневого давления.
3- й случай - склон устойчив, в связи с чем действительной поверхности скольжения в натурных условиях не существует. Однако на склоне требуется выполнить какие-то планировочные работы, пригрузить его зданиями и сооружениями или учесть возможное изменение гидрологических условий, в результате чего напряженное состояние грунтов склона изменится. При этом по расчетам (с принятием φ факт , c факт и некоторой возможной поверхности скольжения) получается, что после указанных изменений склон может прийти к состоянию, близкому к предельному равновесию. В таком случае для новой конфигурации склона (с учетом планировочных работ) с учетом пригрузки от сооружений или изменения гидрогеологических условий производится поиск наиболее опасной поверхности скольжения методом подбора и уточнение обратными расчетами c и φ при экстремальной поверхности скольжения - аналогично тому, как это описано для 2-го случая.
4- й случай - склон устойчив при естественной его поверхности или с учетом планировочных и пригрузочных работ, а также прогнозируемых гидрогеологических условий. Однако этот склон находится в сейсмическом районе и если учесть сейсмические силы для соответствующей балльности района по сейсмике, то расчеты показывают, что склон может прийти к состоянию, близкому к предельному равновесию. В таком случае весь расчет производится аналогично описанному во 2-м случае, однако, во всех вычислениях учитывается сейсмическая сила. С ее учетом устанавливается экстремальная поверхность скольжения, уточняются прочностные характеристики φ и c (исходя из K у (с учетом сейсмики) ≈ 1) и по ним строится эпюра оползневого давления (причем при определении E оп также учитывается сейсмика).
5- й случай - склон, находящийся в сейсмическом районе, неустойчив по расчету даже без учета сейсмических сил. В таком случае все расчеты выполняются аналогично описанным во 2-м случае, без учета сейсмических сил - вплоть до построения эпюры оползневого давления. При определении же оползневого давления E оп учитываются и сейсмические силы.
6- й случай - в склоне действует гидродинамическое давление грунтовых вод. В этом случае все расчеты выполняются аналогично предыдущим, однако, во всех вычислениях добавляется величина гидродинамического давления.
Кстати, гидродинамическое давление должно учитываться всегда, когда есть наклонная депрессионная кривая уровня грунтовых вод (рис. 31). Для учета фильтрационных сил упрощенным способом, как указывалось в главе I , требуется лишь построение именно этой кривой депрессии. Напоминаем, что этот упрощенный способ заключается в следующем:
сдвиговые характеристики грунта в уровне поверхности скольжения принимаются для случая его водонасыщения ( c в , φ в );
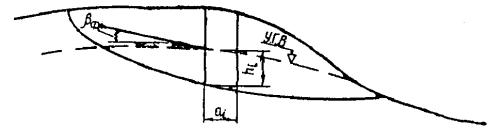
Рис. 31 . Учет действия грунтовых вод
собственный вес грунта во всех расчетах принимается с учетом взвешивания в воде части оползневого отсека между кривой депрессии и поверхностью скольжения, т.е. объемный вес грунта принимается за вычетом объемного веса воды ( γ - γω ); разумеется, взвешивание водой требуется учитывать для тех слоев оползневой толщи, для которых оно обычно учитывается в механике грунтов (например, для глин взвешивающее действие воды обычно не учитывается);
к величине сдвигающей силы в каждом отсеке добавляется величина гидродинамического давления (см. формулу ( 8)):
ji = aihi γωsin β ф i , ( 139)
где sin β ф i = ii есть градиент, т.е. падение напора на единицу длины тока воды (принимается, что уклон кривой депрессии совпадает с наклоном равнодействующей гидродинамического давления);
ai , hi , β ф i - параметры, понятные из рис. 31.
При отсутствии напорных грунтовых вод и наличии обычного водонасыщения грунтов откоса в расчете коэффициента устойчивости или величины оползневого давления учитываются лишь все физико-механические и прочностные характеристики пород в замоченном состоянии; взвешивающее же действие воды или гидродинамическое давление в таком случае не учитываются.
Нередко вызывает затруднение уточнение прочностных характеристик грунтов с помощью обратных расчетов, ибо не всегда ясно, что варьировать - φ или c . Обычно соотношение φ и c должно, как правило, исходить из принятия одного из минимальных значений φ и подбора c . Однако здесь возможны варианты - при преобладающем количестве песчаных частиц в грунтах, расположенных в уровне поверхности скольжения, следует минимизировать φ, а при глинистых грунтах следует минимизировать c . Здесь необходимо решать вопрос, исходя из конкретных условий и просчитывая на ЭВМ различные варианты. В самом начале расчета, вероятно, целесообразно исходить из условия, что в грунтах, которые можно отнести к щебенистым, супесчаным, пескам и т.д. следует принимать минимальное значение φ и с помощью обратных расчетов уточнять c ; в грунтах, которые можно отнести к глинистым (суглинки, глины и т.д.) необходимо принимать минимальное значение c и уточнять значение φ. При этом сдвиговые характеристики по основной протяженности поверхности скольжения (вс на рис. 29), как правило, принимаются постоянными, а на нисходящей (ав) и восходящей ( cd ) ветвях поверхности скольжения могут приниматься свои сдвиговые характеристики, определенные непосредственно для пересекаемых поверхностью скольжения грунтов и сниженные с учетом их возможного замачивания.
Кстати, при расчете устойчивости склона на переползание через противооползневую конструкцию сдвиговые характеристики принимаются: для грунтов в уровне основной протяженности поверхности скольжения - характеристики, уточненные обратными расчетами по устойчивости всего склона; для грунтов в уровне восходящей ветви поверхности скольжения - сдвиговые характеристики для естественного состояния грунтов.
При построении эпюры оползневого давления часто важным является учет отпора грунта, расположенного ниже проектируемых удерживающих конструкций.
Величина отпора определяется из рассмотрения устойчивости части склона, расположенной ниже самой нижней конструкции. Например, для склона, представленного на рис. 32, величина отпора может быть определена из рассмотрения удерживающих и сдвигающих сил для части склона СД :
E отп = ΣQ уд(СД) - K у(отп) ΣQ сдв(СД) , ( 140)
где K у(отп) - коэффициент устойчивости склона, принимаемый для данного расчета (см. ниже).
Получающаяся величина отпора E отп может отниматься от ординат ранее построенной эпюры оползневого давления, разделяясь пропорционально, например, жесткости удерживающих конструкций, под которыми эти ординаты расположены.
Дело в том, что во всех используемых методах расчета устойчивости, как было указано выше, принимается гипотеза затвердевшего тела - призма возможного смещения рассматривается в виде затвердевшего клина. При таком допущении в расчете общей устойчивости склона участвуют все силы по всей протяженности склона, в связи с чем отпор может быть определенным образом распределен между силами, действующими в вышележащей части склона.
После отнятия сил отпора первоначально построенная эпюра abcd оползневого давления заменяется уменьшенной эпюрой ab ' c ' d ' (см. рис. 32) и расчет удерживающих конструкций ведется на усилия, изображаемые уменьшенными на величину отпора ординатами (вместо ob - b ' ; вместо o ' c - o ' c ' ).
Величины коэффициентов устойчивости склона, в соответствии с указанным выше и работами [ 4, 6, 10], принимаются в зависимости от назначения их использования: для определения оползневого давления - Kуз = 1,01 - 1,10; для определения величины отпора - Kу(отп) = 1,1 - 1,2; при расчете общей устойчивости склона допускаемый коэффициент устойчивости [ K у ] ≥ 1,2 (в зависимости от класса сооружений на склоне).
При расчете коэффициента устойчивости укрепленного склона учитываются удерживающие и сдвигающие силы, действующие в грунтах по поверхности скольжения, а также любое другое противодействие смещению грунтов массива, выраженное в силовой или моментной форме [ 10]. При укреплении склона противооползневыми удерживающими свайными конструкциями такое противодействие удобней всего выражать в виде усилий среза свай, в то время как сами конструкции, для обеспечения их устойчивости, следует рассчитывать на изгиб от действия горизонтальной силы оползневого давления. Допускается противодействие конструкций учитывать в виде силы воспринимаемого ими оползневого давления.
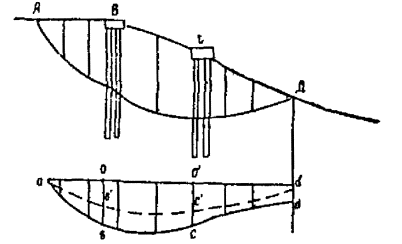
Рис. 32 . Учет отпора нижележащего грунта
Следует отметить, что при пользовании формулами ( 136), ( 137), ( 140), а также выражениями для определения оползневого давления по методам Маслова или Шахунянца, необходимо применять коэффициенты сочетания нагрузок, надежности и условий работы, приведенные в инструкции [ 10], увязывая их со значениями принимаемых коэффициентов Kуз и K у(отп) [ 6].
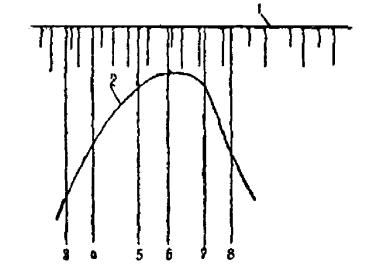
Рис. 33 . Схема оползневого склона в плане:
1 - бровка склона; 2 - контур оползня; 3 - 8 - расчетные поперечники
Требуется еще отметить, что указанные в настоящем параграфе расчеты должны на каждом конкретном склоне выполняться для серии расчетных поперечников (рис. 33), которые намечаются из таких соображений, чтобы как можно полнее охватить все разнообразие инженерно-геологических условий площадки, конфигураций поверхности склона и поверхности скольжения, возможное изменение контуров оползня в плане (на перспективу) и т.д. Расположение характерных поперечников, как правило, должно устанавливаться в процессе инженерно-геологических изысканий, и их подробные профили необходимо приводить в отчете по изысканиям. Если в процессе проектирования противооползневых конструкций станет ясно, что приведенных в отчете поперечников недостаточно, чтобы полнее охватить территорию склона, на которой возможны оползневые подвижки, проектировщикам следует самим строить дополнительные поперечники, исходя из имеющихся в отчете по инженерно-геологическим изысканиям отметок поверхности склона, геологических выработок, расположения литологических слоев, уровня подземных вод и т.д. В любом случае вся площадь оползнеопасной территории склона должна быть обсчитана по серии расчетных поперечников в соответствии с изложенными выше положениями.
При соблюдении приведенных принципов построения эпюры оползневого давления и расчета противооползневых сооружений по этим величинам давлений, как показывает опыт, обеспечивается надежное укрепление склонов.
ЗАКЛЮЧЕНИЕ
Настоящие рекомендации по выбору методов расчета коэффициента устойчивости склона и величины оползневого давления предназначены для проектирования противооползневых мероприятий и удерживающих конструкций, а также установления степени устойчивости склонов, на которых производятся специальные и монтажные работы.
По существу данные рекомендации заменят поиск необходимых способов расчета в технической литературе, который необходимо было производить в каждом случае расчета устойчивости склона и величины оползневого давления.
Рекомендуемые методы расчета, во-первых, проверены с помощью теоретических и экспериментальных исследований, во-вторых, апробированы с помощью большого количества практических случаев.
На основе приведенных рекомендаций Укрспецстройпроектом запроектированы противооползневые мероприятия и противооползневые удерживающие свайные конструкции более чем на 200 объектах в Крыму, на Кавказе, в Закарпатской области, в Смоленской области, на Украине и во многих других местах. На всех этих объектах укрепленные склоны нормально эксплуатируются.
В связи с этим предлагаемые методы расчета и принципы построения эпюры оползневого давления могут быть рекомендованы к самому широкому применению.
ПРИЛОЖЕНИЕ
ТАБЛИЦЫ ДЛЯ РАСЧЕТА ОПОЛЗНЕВОГО ДАВЛЕНИЯ УСКОРЕННЫМ СПОСОБОМ
Таблица 1
Значения e oi = K у sin α i - cos α i tg φi
|
αi град (рад) |
e oi при φ i в град (рад) |
||||||||||
|
0 (0) |
4 (0,0698) |
6 (0,105) |
8 (0,140) |
10 (0,174) |
12 (0,209) |
16 (0,279) |
20 (0,349) |
24 (0,419) |
28 (0,489) |
30 (0,524) |
|
|
K у = 1,00 |
|||||||||||
|
-30 (-0,524) |
-0,5000 |
-0,5606 |
-0,5910 |
-0,6217 |
-0,6527 |
-0,6841 |
-0,7483 |
-0,8152 |
-0,8856 |
-0,9605 |
-1,0000 |
|
-25 (-0,436) |
-0,4226 |
-0,4860 |
-0,5179 |
-0,5500 |
-0,5824 |
-0,6153 |
-0,6825 |
-0,7525 |
-0,8261 |
-0,9045 |
-0,9459 |
|
-20 (-0,349) |
-0,3420 |
-0,4077 |
-0,4408 |
-0,4741 |
-0,5077 |
-0,5418 |
-0,6115 |
-0,6840 |
-0,7604 |
-0,8417 |
-0,8846 |
|
-15 (-0,262) |
-0,2588 |
-0,3264 |
-0,3603 |
-0,3946 |
-0,4291 |
-0,4641 |
-0,5358 |
-0,6104 |
-0,6889 |
-0,7724 |
-0,8165 |
|
-10 (-0,174) |
-0,1736 |
-0,2425 |
-0,2772 |
-0,3121 |
-0,3473 |
-0,3830 |
-0,4560 |
-0,5321 |
-0,6121 |
-0,6973 |
-0,7422 |
|
-5 (-0,0873) |
-0,0872 |
-0,1568 |
-0,1919 |
-0,2272 |
-0,2628- |
-0,2989 |
-0,3728 |
-0,4497 |
-0,5307 |
-0,6168 |
-0,6623 |
|
0 (0,0000) |
-0,0000 |
-0,0699 |
-0,1051 |
-0,1405 |
-0,1763 |
-0,2126 |
-0,2867 |
-0,3640 |
-0,4452 |
-0,5317 |
-0,5774 |
|
5 (0,0873) |
0,0872 |
0,0175 |
-0,0175 |
-0,0529 |
-0,0885 |
-0,1246 |
-0,1985 |
-0,2754 |
-0,3564 |
-0,4425 |
-0,4880 |
|
10 (0,174) |
0,1736 |
0,1048 |
0,0701 |
0,0352 |
0,0000 |
-0,0357 |
-0,1087 |
-0,1848 |
-0,2648 |
-0,3500 |
-0,3949 |
|
15 (0,262) |
0,2588 |
0,1913 |
0,1573 |
0,1231 |
0,0885 |
0,0535 |
-0,0182 |
-0,0927 |
-0,1712 |
-0,2548 |
-0,2989 |
|
20 (0,349) |
0,3420 |
0,2763 |
0,2433 |
0,2100 |
0,1763 |
0,1423 |
0,0726 |
0,0000 |
-0,0764 |
-0,1576 |
-0,2005 |
|
25 (0,436) |
0,4226 |
0,3592 |
0,3274 |
0,2952 |
0,2628 |
0,2300 |
0,1627 |
0,0927 |
0,0191 |
-0,0593 |
-0,1006 |
|
30 (0,524) |
0,5000 |
0,4394 |
0,4090 |
0,3783 |
0,3473 |
0,3159 |
0,2517 |
0,1848 |
0,1144 |
0,0395 |
0,0000 |
|
35 (0,611) |
0,5736 |
0,5163 |
0,4875 |
0,4585 |
0,4291 |
0,3995 |
0,3387 |
0,2754 |
0,2089 |
0,1380 |
0,1006 |
|
40 (0,698) |
0,6428 |
0,5892 |
0,5623 |
0,5351 |
0,5077 |
0,4800 |
0,4231 |
0,3640 |
0,3017 |
0,2355 |
0,2005 |
|
45 (0,785) |
0,7071 |
0,6577 |
0,6328 |
0,6077 |
0,5824 |
0,5568 |
0,5043 |
0,4497 |
0,3923 |
0,3311 |
0,2989 |
|
50 (0,873) |
0,7660 |
0,7211 |
0,6985 |
0,6757 |
0,6527 |
0,6294 |
0,5817 |
0,5321 |
0,4799 |
0,4243 |
0,3949 |
|
55 (0,960) |
0,8192 |
0,7790 |
0,7589 |
0,7385 |
0,7180 |
0,6972 |
0,6547 |
0,6104 |
0,5638 |
0,5142 |
0,4880 |
|
60 (1,050) |
0,8660 |
0,8311 |
0,8135 |
0,7958 |
0,7779 |
0,7597 |
0,7227 |
0,6840 |
0,6434 |
0,6002 |
0,5774 |
|
65 (1,138) |
0,9063 |
0,8768 |
0,8619 |
0,8469 |
0,8318 |
0,8165 |
0,7851 |
0,7525 |
0,7181 |
0,6816 |
0,6623 |
|
70 (1,225) |
0,9397 |
0,9158 |
0,9037 |
0,8916 |
0,8794 |
0,8670 |
0,8416 |
0,8152 |
0,7874 |
0,7578 |
0,7422 |
|
75 (1,312) |
0,9659 |
0,9478 |
0,9387 |
0,9296 |
0,9203 |
0,9109 |
0,8917 |
0,8717 |
0,8507 |
0,8283 |
0,8165 |
|
80 (1,400) |
0,9848 |
0,9727 |
0,9666 |
0,9604 |
0,9542 |
0,9479 |
0,9350 |
0,9216 |
0,9075 |
0,8925 |
0,8846 |
|
K у = 1,03 |
|||||||||||
|
-30 (-0,524) |
-0,5150 |
-0,5756 |
-0,6060 |
-0,6367 |
-0,6677 |
-0,6991 |
-0,7633 |
-0,8302 |
-0,9006 |
-0,9755 |
-1,0150 |
|
-25 (-0,436) |
-0,4353 |
-0,4987 |
-0,5306 |
-0,5627 |
-0,5951 |
-0,6279 |
-0,6952 |
-0,7652 |
-0,8388 |
-0,9172 |
-0,9586 |
|
-20 (-0,349) |
-0,3523 |
-0,4180 |
-0,4510 |
-0,4843 |
-0,5180 |
-0,5520 |
-0,6217 |
-0,6943 |
-0,7707 |
-0,8519 |
-0,8948 |
|
-15 (-0,262) |
-0,2666 |
-0,3341 |
-0,3681 |
-0,4023 |
-0,4369 |
-0,4719 |
-0,5436 |
-0,6182 |
-0,6966 |
-0,7802 |
-0,8243 |
|
-10 (-0,174) |
-0,1789 |
-0,2477 |
-0,2824 |
-0,3173 |
-0,3525 |
-0,3882 |
-0,4612 |
-0,5373 |
-0,6173 |
-0,7025 |
-0,7474 |
|
-5 (-0,0873) |
-0,0898 |
-0,1594 |
-0,1945 |
-0,2298 |
-0,2654 |
-0,3015 |
-0,3754 |
-0,4524 |
-0,5333 |
-0,6195 |
-0,6649 |
|
0 (0,0000) |
0,0000 |
-0,0699 |
-0,1051 |
-0,1405 |
-0,1763 |
-0,2126 |
-0,2867 |
-0,3640 |
-0,4452 |
-0,5317 |
-0,5774 |
|
5 (0,0873) |
0,0898 |
0,0201 |
-0,0149 |
-0,0502 |
-0,0859 |
-0,1220 |
-0,1956 |
-0,2728 |
-0,3538 |
-0,4399 |
-0,4854 |
|
10 (0,174) |
0,1789 |
0,1100 |
0,0754 |
0,0405 |
0,0052 |
-0,0305 |
-0,1035 |
-0,1796 |
-0,2596 |
-0,3448 |
-0,3897 |
|
15 (0,262) |
0,2666 |
0,1990 |
0,1651 |
0,1308 |
0,0963 |
0,0613 |
-0,0104 |
-0,0850 |
-0,1635 |
-0,2470 |
-0,2911 |
|
20 (0,349) |
0,3523 |
0,2866 |
0,2535 |
0,2202 |
0,1866 |
0,1525 |
0,0828 |
0,0103 |
-0,0661 |
-0,1474 |
-0,1903 |
|
25 (0,436) |
0,4353 |
0,3719 |
0,3400 |
0,3079 |
0,2755 |
0,2427 |
0,1754 |
0,1054 |
0,0318 |
-0,0466 |
-0,0880 |
|
30 (0,524) |
0,5150 |
0,4544 |
0,4240 |
0,3933 |
0,3623 |
0,3309 |
0,2667 |
0,1998 |
0,1294 |
0,0545 |
0,0150 |
|
35 (0,611) |
0,5908 |
0,5335 |
0,5047 |
0,4757 |
0,4463 |
0,4167 |
0,3559 |
0,2926 |
0,2261 |
0,1552 |
0,1178 |
|
40 (0,698) |
0,6621 |
0,6085 |
0,5816 |
0,5544 |
0,5270 |
0,4992 |
0,4424 |
0,3833 |
0,3210 |
0,2548 |
0,2198 |
|
45 (0,785) |
0,7283 |
0,6789 |
0,6540 |
0,6289 |
0,6036 |
0,5780 |
0,5256 |
0,4710 |
0,4135 |
0,3523 |
0,3201 |
|
50 (0,873) |
0,7890 |
0,7441 |
0,7215 |
0,6987 |
0,6757 |
0,6524 |
0,6047 |
0,5551 |
0,5028 |
0,4472 |
0,4179 |
|
55 (0,960) |
0,8437 |
0,8036 |
0,7834 |
0,7631 |
0,7426 |
0,7218 |
0,6793 |
0,6350 |
0,5884 |
0,5388 |
0,5126 |
|
60 (1,050) |
0,8920 |
0,8570 |
0,8395 |
0,8217 |
0,8038 |
0,7857 |
0,7486 |
0,7100 |
0,6694 |
0,6262 |
0,6033 |
|
65 (1,138) |
0,9335 |
0,9039 |
0,8891 |
0,8741 |
0,8590 |
0,8437 |
0,8123 |
0,7797 |
0,7453 |
0,7088 |
0,6895 |
|
70 (1,225) |
0,9679 |
0,9440 |
0,9319 |
0,9198 |
0,9076 |
0,8952 |
0,8698 |
0,8434 |
0,8156 |
0,7860 |
0,7704 |
|
75 (1,312) |
0,9929 |
0,9768 |
0,9677 |
0,9585 |
0,9493 |
0,9399 |
0,9207 |
0,9007 |
0,8797 |
0,8573 |
0,8455 |
|
80 (1,400) |
1,0144 |
1,0022 |
0,9961 |
0,9899 |
0,9837 |
0,9774 |
0,9646 |
0,9511 |
0,9370 |
0,9220 |
0,9141 |
|
Kу = 1,05 |
|||||||||||
|
-30 (-0,524) |
-0,5250 |
-0,5856 |
-0,6160 |
-0,6467 |
-0,6777 |
-0,7091 |
-0,7733 |
-0,8402 |
-0,9106 |
-0,9855 |
-1,0250 |
|
-25 (-0,436) |
-0,4437 |
-0,507 |
-0,5390 |
-0,5711 |
-0,6036 |
-0,6364 |
-0,7036 |
-0,7736 |
-0,8473 |
-0,9256 |
-0,9670 |
|
-20 (-0,349) |
-0,3591 |
-0,4248 |
-0,4579 |
-0,4912 |
-0,5248 |
-0,5589 |
-0,6286 |
-0,7011 |
-0,7775 |
-0,8588 |
-0,9017 |
|
-15 (-0,262) |
-0,2718 |
-0,3393 |
-0,3733 |
-0,4075 |
-0,4421 |
-0,4771 |
-0,5487 |
-0,6233 |
-0,7018 |
-0,7854 |
-0,8294 |
|
-10 (-0,174) |
-0,1823 |
-0,2512 |
-0,2858 |
-0,3207 |
-0,3560 |
-0,3917 |
-0,4647 |
-0,5408 |
-0,6208 |
-0,7060 |
-0,7509 |
|
-5 (-0,0873) |
-0,0915 |
-6,1612 |
-0,1962 |
-0,2315 |
-0,2672 |
-0,3033 |
-0,3772 |
-0,4541 |
-0,5350 |
-0,6212 |
-0,6667 |
|
0 (0,0000) |
0,0000 |
-0,0699 |
-0,1051 |
-0,1405 |
-0,1763 |
-0,2126 |
-0,2867 |
-0,3640 |
-0,4452 |
-0,5317 |
-0,5774 |
|
5 (0,0873) |
0,0915 |
0,0219 |
-0,0132 |
-0,0485 |
-0,0841 |
-0,1202 |
-0,1941 |
-0,2711 |
-0,3520 |
-0,4382 |
-0,4836 |
|
10 (0,174) |
0,1823 |
0,1135 |
0,0788 |
0,0439 |
0,0087 |
-0,0270 |
-0,1001 |
-0,1761 |
-0,2561 |
-0,3413 |
-0,3862 |
|
15 (0,262) |
0,2718 |
0,2042 |
0,1702 |
0,1360 |
0,1011 |
0,0664 |
-0,0052 |
-0,0798 |
-0,1583 |
-0,2418 |
-0,2859 |
|
20 (0,349) |
0,3591 |
0,2934 |
0,2604 |
0,2271 |
0,1934 |
0,1594 |
0,0897 |
0,0171 |
-0,0593 |
-0,1405 |
-0,1834 |
|
25 (0,436) |
0,4437 |
0,3804 |
0,3485 |
0,3164 |
0,2839 |
0,2511 |
0,1839 |
0,1139 |
0,0402 |
-0,0381 |
-0,0795 |
|
30 (0,524) |
0,5250 |
0,4644 |
0,4340 |
0,4033 |
0,3723 |
0,3409 |
0,2767 |
0,2098 |
0,1394 |
0,0645 |
0,0250 |
|
35 (0,611) |
0,6023 |
0,5450 |
0,5162 |
0,4871 |
0,4578 |
0,4281 |
0,3674 |
0,3041 |
0,2375 |
0,1667 |
0,1293 |
|
40 (0,698) |
0,6749 |
0,6214 |
0,5944 |
0,5673 |
0,5399 |
0,5121 |
0,4553 |
0,3961 |
0,3339 |
0,2676 |
0,2327 |
|
45 (0,785) |
0,7425 |
0,6930 |
0,6681 |
0,6431 |
0,6178 |
0,5922 |
0,5397 |
0,4851 |
0,4276 |
0,3665 |
0,3342 |
|
50 (0,873) |
0,8043 |
0,7594 |
0,7368 |
0,7140 |
0,6910 |
0,6677 |
0,6200 |
0,5704 |
0,5182 |
0,4626 |
0,4332 |
|
55 (0,960) |
0,8601 |
0,8200 |
0,7998 |
0,7795 |
0,7590 |
0,7382 |
0,6956 |
0,6513 |
0,6047 |
0,5551 |
0,5290 |
|
60 (1,050) |
0,9093 |
0,8744 |
0,8568 |
0,8391 |
0,8212 |
0,8030 |
0,7660 |
0,7273 |
0,6867 |
0,6435 |
0,6207 |
|
65 (1,138) |
0,9516 |
0,9221 |
0,9072 |
0,8922 |
0,8771 |
0,8618 |
0,8304 |
0,7978 |
0,7635 |
0,7269 |
0,7076 |
|
70 (1,225) |
0,9867 |
0,9628 |
0,9507 |
0,9386 |
0,9264 |
0,9140 |
0,8886 |
0,8622 |
0,8344 |
0,8048 |
0,7892 |
|
75 (1,312) |
1,0142 |
0,9961 |
0,9870 |
0,9778 |
0,9686 |
0,9592 |
0,9400 |
0,9200 |
0,8990 |
0,8766 |
0,8648 |
|
80 (1,400) |
1,0340 |
1,0219 |
1,0158 |
1,0096 |
1,0034 |
0,9971 |
0,9843 |
0,9708 |
0,9567 |
0,9417 |
0,9338 |
|
Kу = 1,07 |
|||||||||||
|
-30 (-0,524) |
-0,5350 |
-0,5956 |
-0,6260 |
-0,6567 |
-0,6877 |
-0,7191 |
-0,7833 |
-0,8502 |
-0,9206 |
-0,9955 |
-1,0350 |
|
-25 (-0,436) |
-0,4522 |
-0,5156 |
-0,5475 |
-0,5796 |
-0,6120 |
-0,6448 |
-0,7121 |
-0,7821 |
-0,8557 |
-0,9341 |
-0,9755 |
|
-20 (-0,349) |
-0,3660 |
-0,4317 |
-0,4647 |
-0,4980 |
-0,5317 |
-0,5657 |
-0,6354 |
-0,7080 |
-0,7843 |
-0,8656 |
-0,9085 |
|
-15 (-0,262) |
-0,2769 |
-0,3445 |
-0,3785 |
-0,4127 |
-0,4473 |
-0,4823 |
-0,5539 |
-0,6285 |
-0,7070 |
-0,7905 |
-0,8346 |
|
-10 (-0,174) |
-0,1858 |
-0,2547 |
-0,2893 |
-0,3242 |
-0,3595 |
-0,3951 |
-0,4682 |
-0,5442 |
-0,6243 |
-0,7094 |
-0,7544 |
|
-5 (-0,0873) |
-0,0933 |
-0,1629 |
-0,1980 |
-0,2333 |
-0,2689 |
-0,3050 |
-0,3789 |
-0,4558 |
-0,5368 |
-0,6229 |
-0,6684 |
|
0 (0,0000) |
0,0000 |
-0,0699 |
-0,1051 |
-0,1405 |
-0,1763 |
-0,2126 |
-0,2867 |
-0,3640 |
-0,4452 |
-0,5317 |
-0,5774 |
|
5 (0,0873) |
0,0933 |
0,0236 |
-0,0114 |
-0,0467 |
-0,0824 |
-0,1185 |
-0,1924 |
-0,2693 |
-0,3503 |
-0,4364 |
-0,4819 |
|
10 (0,174) |
0,1858 |
0,1169» |
0,0823 |
0,0474 |
0,0122 |
-0,0235 |
-0,0966 |
-0,1726 |
-0,2527 |
-0,3378 |
-0,3828 |
|
15 (0,262) |
0,2769 |
0,2094 |
0,1754 |
0,1412 |
0,1066 |
0,0716 |
-0,0000 |
-0,0746 |
-0,1531 |
-0,2367 |
-0,2807 |
|
20 (0,349) |
0,3660 |
0,3003 |
0,2672 |
0,2339 |
0,2003 |
0,1662 |
0,0965 |
0,0239 |
-0,0524 |
-0,1337 |
-0,1766 |
|
25 (0,436) |
0,4522 |
0,3888 |
0,3569 |
0,3248 |
0,2924 |
0,2596 |
0,1923 |
0,1223 |
0,0487 |
-0,0297 |
-0,0711 |
|
30 (0,524) |
0,5350 |
0,4744 |
0,4440 |
0,4133 |
0,3823 |
0,3509 |
0,2867 |
0,2198 |
0,1494 |
0,0745 |
0,0350 |
|
35 (0,611) |
0,6137 |
0,5564 |
0,5276 |
0,4986 |
0,4693 |
0,4396 |
0,3788 |
0,3155 |
0,2490 |
0,1782 |
0,1408 |
|
40 (0,698) |
0,6878 |
0,6342 |
0,6073 |
0,5801 |
0,5527 |
0,5250 |
0,4681 |
0,4090 |
0,3467 |
0,2805 |
0,2455 |
|
45 (0,785) |
0,7566 |
0,7072 |
0,6823 |
0,6572 |
0,6319 |
0,6063 |
0,5538 |
0,4992 |
0,4418 |
0,3806 |
0,3484 |
|
50 (0,873) |
0,8197 |
0,7747 |
0,7521 |
0,7293 |
0,7063 |
0,6830 |
0,6354 |
0,5857 |
0,5335 |
0,4779 |
0,4486 |
|
55 (0,960) |
0,8765 |
0,8364 |
0,8162 |
0,7959 |
0,7754 |
0,7546 |
0,7120 |
0,6677 |
0,6211 |
0,5715 |
0,5453 |
|
60 (1,050) |
0,9266 |
0,8917 |
0,8741 |
0,8564 |
0,8385 |
0,8204 |
0,7833 |
0,7447 |
0,7040 |
0,6608 |
0,6380 |
|
65 (1,138) |
0,9697 |
0,9402 |
0,9253 |
0,9104 |
0,8952 |
0,8799 |
0,8486 |
0,8159 |
0,7816 |
0,7450 |
0,7258 |
|
70 (1,225) |
1,0055 |
0,9816 |
0,9695 |
0,9574 |
0,9452 |
0,9328 |
0,9074 |
0,8810 |
0,8532 |
6,8236 |
0,8080 |
|
75 (1,312) |
1,0335 |
1,0154 |
1,0063 |
0,9972 |
0,9879 |
0,9785 |
0,9593 |
0,9393 |
0,9183 |
0,8959 |
0,8841 |
|
80 (1,400) |
1,0537 |
1,0416 |
1,0355 |
1,0293 |
1,0231 |
1,0168 |
1,0040 |
0,9905 |
0,9764 |
0,9614 |
0,9535 |
|
Kу = 1,10 |
|||||||||||
|
-30 (-0,524) |
-0,5500 |
-0,6106 |
-0,6410 |
-0,6717 |
-0,7027 |
-0,7341 |
-0,7983 |
-0,8652 |
-0,9356 |
-1,0105 |
-1,0500 |
|
-25 (-0,436) |
-0,4649 |
-0,5283 |
-0,5601 |
-0,5923 |
-0,6247 |
-0,6575 |
-0,7248 |
-0,7947 |
-0,8684 |
-0,9463 |
-0,9881 |
|
-20 (0,349) |
-0,3762 |
-0,4419 |
-0,4750 |
-0,5083 |
-0,5419 |
-0,5760 |
-0,6457 |
-0,7182 |
-0,7946 |
-0,8759 |
-0,9188 |
|
-15 (-0,262) |
-0,2847 |
-0,3522 |
-0,3862 |
-0,4205 |
-0,4550 |
-0,4900 |
-0,5617 |
-0,6363 |
-0,7148 |
-0,7983 |
-0,8424 |
|
-10 (-0,174) |
-0,1910 |
-0,2599 |
-0,2945 |
-0,3294 |
-0,3647 |
-0,4003 |
-0,4734 |
-0,5495 |
-0,6295 |
-0,7146 |
-0,7596 |
|
-5 (-0,0873) |
-0,0959 |
-0,1655 |
-0,2006 |
-0,2359 |
-0,2715 |
-0,3076 |
-0,3815 |
-0,4585 |
-0,5394 |
-0,6256 |
-0,6710 |
|
0 (0) |
0,0000 |
-0,0699 |
-0,1051 |
-0,1405 |
-0,1763 |
-0,2126 |
-0,2857 |
-0,3640 |
-0,4452 |
-0,5317 |
-0,5774 |
|
5 (0,0873) |
0,0959 |
0,0262 |
-0,0088 |
-0,0441 |
-0,0798 |
-0,1159 |
-0,1898 |
-0,2667 |
-0,3477 |
-0,4338 |
-0,4793 |
|
10 (0,174) |
0,1910 |
0,1221 |
0,0875 |
0,0526 |
0,0174 |
-0,0183 |
-0,0914 |
-0,1674 |
-0,2475 |
-0,3326 |
-0,3776 |
|
15 (0,262) |
0,2847 |
0,2172 |
0,1832 |
0,1489 |
0,1144 |
0,0794 |
0,0077 |
-0,0669 |
-0,1454 |
-0,2289 |
-0,2730 |
|
20 (0,349) |
0,3762 |
0,3105 |
0,2775 |
0,2442 |
0,2105 |
0,1765 |
0,1068 |
0,0342 |
-0,0422 |
-0,1234 |
-0,1663 |
|
25 (0,436) |
0,4649 |
0,4015 |
0,3696 |
0,3375 |
0,3051 |
0,2722 |
0,2050 |
0,1350 |
0,0614 |
-0,0170 |
-0,0584 |
|
30 (0,524) |
0,5500 |
0,4894 |
0,4590 |
0,4283 |
0,3973 |
0,3659 |
0,3017 |
0,2348 |
0,1644 |
0,0895 |
0,0500 |
|
35 (0,611) |
0,6309 |
0,5737 |
0,5448 |
0,5158 |
0,4865 |
0,4568 |
0,3960 |
0,3328 |
0,2662 |
0,1954 |
0,1580 |
|
40 (0,698) |
0,7071 |
0,6535 |
0,6266 |
0,5994 |
0,5720 |
0,5442 |
0,4874 |
0,4282 |
0,3660 |
0,2998 |
0,2648 |
|
45 (0,785) |
0,7778 |
0,7284 |
0,7035 |
0,6784 |
0,6531 |
0,6275 |
0,5751 |
0,5205 |
0,4630 |
0,4018 |
0,3696 |
|
50 (0,873) |
0,8426 |
0,7977 |
0,7751 |
0,7523 |
0,7293 |
0,7060 |
0,6583 |
0,6087 |
0,5565 |
0,5009 |
0,4715 |
|
55 (0,960) |
0,9011 |
0,8610 |
0,8408 |
0,8205 |
0,7999 |
0,7791 |
0,7366 |
0,6923 |
0,6457 |
0,5961 |
0,5699 |
|
60 (1,050) |
0,9526 |
0,9177 |
0,9001 |
0,8824 |
0,8645 |
0,8463 |
0,8093 |
0,7706 |
0,7300 |
0,6868 |
0,6640 |
|
65 (1,138) |
0,9969 |
0,9674 |
0,9525 |
0,9375 |
0,9224 |
0,9071 |
0,8758 |
0,8431 |
0,8088 |
0,7722 |
0,7529 |
|
70 (1,225) |
1,0337 |
1,0097 |
0,9977 |
0,9856 |
0,9734 |
0,9610 |
0,9356 |
0,9092 |
0,8814 |
0,8518 |
0,8362 |
|
75 (1,312) |
1,0625 |
1,0444 |
1,0353 |
1,0261 |
1,0169 |
1,0075 |
0,9883 |
0,9683 |
0,9473 |
0,9249 |
0,9131 |
|
80 (1,400) |
1,0833 |
1,0711 |
1,0650 |
1,0589 |
1,0527 |
1,0464 |
1,0335 |
1,0201 |
1,0060 |
0,9910 |
0,9830 |
|
K у = 1,20 |
|||||||||||
|
-30 (-0,524) |
-0,6000 |
-0,6606 |
-0,6910 |
-0,7217 |
-0,7527 |
-0,7841 |
-0,8483 |
-0,9152 |
-0,9856 |
-1,0605 |
-1,1000 |
|
-25 (-0,436) |
-0,5071 |
-0,5705 |
-0,6024 |
-0,6345 |
-0,6669 |
-0,6998 |
-0,7670 |
-0,8370 |
-0,9107 |
-0,9890 |
-1,0304 |
|
-20 (-0,349) |
-0,4104 |
-0,4761 |
-0,5092 |
-0,5425 |
-0,5761 |
-0,6102 |
-0,6799 |
-0,7524 |
-0,8288 |
-0,9101 |
-0,9530 |
|
-15 (-0,262) |
-0,3106 |
-0,3781 |
-0,4121 |
-0,4463 |
-0,4809 |
-0,5159 |
-0,5876 |
-0,6622 |
-0,7406 |
-0,8242 |
-0,8683 |
|
-10 (-0,174) |
-0,2084 |
-0,2772 |
-0,3119 |
-0,3468 |
-0,3820 |
-0,4177 |
-0,4908 |
-0,5668 |
-0,6468 |
-0,7320 |
-0,7770 |
|
-5 (-0,0873) |
-0,1046 |
-0,1742 |
-0,2093 |
-0,2446 |
-0,2802 |
-0,3163 |
-0,3902 |
-0,4672 |
-0,5481 |
-0,6343 |
-0,6797 |
|
0 (0,0000) |
0,0000 |
-0,0699 |
-0,1051 |
-0,1405 |
-0,1763 |
-0,2126 |
-0,2867 |
-0,3460 |
-0,4452 |
-0,5317 |
-0,5774 |
|
5 (0,0873) |
0,1046 |
0,0349 |
-0,0001 |
-0,0354 |
-0,0711 |
-0,1072 |
-0,1811 |
-0,2580 |
-0,3389 |
-0,4251 |
-0,4706 |
|
10 (0,174) |
0,2084 |
0,1395 |
0,1049 |
0,0700 |
0,0347 |
-0,0009 |
-0,0740 |
-0,1501 |
-0,2301 |
-0,3153 |
-0,3602 |
|
15 (0,262) |
0,3106 |
0,2430 |
0,2091 |
0,1748 |
0,1403 |
0,1053 |
0,0336 |
-0,0410 |
-0,1195 |
-0,2030 |
-0,2471 |
|
20 (0,349) |
0,4104 |
0,3447 |
0,3117 |
0,2784 |
0,2447 |
0,2107 |
0,1410 |
0,0684 |
-0,0080 |
-0,0892 |
-0,1321 |
|
25,-(0,436) |
0,5071 |
0,4438 |
0,4119 |
0,3798 |
0,3473 |
0,3145 |
0,2473 |
0,1773 |
0,1036 |
0,0252 |
-0,0161 |
|
30 (0,524) |
0,6000 |
0,5394 |
0,5090 |
0,4783 |
0,4473 |
0,4159 |
0,3517 |
0,2848 |
0,2144 |
0,1395 |
0,1000 |
|
35 (0,611) |
0,6883 |
0,6310 |
0,6022 |
0,5732 |
0,5439 |
0,5142 |
0,4534 |
0,3901 |
0,3236 |
0,2527 |
0,2154 |
|
40 (0,698) |
0,7713 |
0,7178 |
0,6908 |
0,6637 |
0,6363 |
0,6085 |
0,5517 |
0,4925 |
0,4303 |
0,3640 |
0,3291 |
|
45 (0,785) |
0,8485 |
0,7991 |
0,7742 |
0,7492 |
0,7238 |
0,6982 |
0,6458 |
0,5912 |
0,5337 |
0,4726 |
0,4403 |
|
50 (0,873) |
0,9193 |
0,8743 |
0,8517 |
0,8289 |
0,8059 |
0,7826 |
0,7349 |
0,6853 |
0,6331 |
0,5775 |
0,5481 |
|
55 (0,960) |
0,9830 |
0,9429 |
0,9227 |
0,9024 |
0,8818 |
0,8611 |
0,8185 |
0,7742 |
0,7276 |
0,6780 |
0,6518 |
|
60 (1,050) |
1,0392 |
1,0043 |
0,9867 |
0,9690 |
0,9511 |
0,9330 |
0,8959 |
0,8572 |
0,8166 |
0,7734 |
0,7506 |
|
65 (1,138) |
1,0876 |
1,0580 |
1,0432 |
1,0282 |
1,0131 |
0,9977 |
0,9664 |
0,9337 |
0,8994 |
0,8629 |
0,8436 |
|
70 (1,225) |
1,1276 |
1,1037 |
1,0917 |
1,0796 |
1,0673 |
1,0549 |
1,0296 |
1,0031 |
0,9754 |
0,9458 |
0,9302 |
|
75 (1,312) |
1,1591 |
1,1410 |
1,1319 |
1,1227 |
1,1135 |
1,1041 |
1,0849 |
1,0649 |
1,0439 |
1,0215 |
1,0097 |
|
80 (1,400) |
1,1818 |
1,1696 |
1,1635 |
1,1574 |
1,1512 |
1,1449 |
1,1320 |
1,1186 |
1,1045 |
1,0894 |
1,0815 |
|
K у = 1,30 |
|||||||||||
|
-30 (-0,524) |
-0,6500 |
-0,7106 |
-0,7410 |
-0,7717 |
-0,8027 |
-0,8341 |
-0,8983 |
-0,9652 |
-1,0356 |
-1,1105 |
-1,1500 |
|
-25 (-0,436) |
-0,5494 |
-0,6128 |
-0,6447 |
-0,6768 |
-0,7092 |
-0,7420 |
-0,8093 |
-0,8793 |
-0,9529 |
-1,0313 |
-1,0727 |
|
-20 (-0,349) |
-0,4446 |
-0,5103 |
-0,5434 |
-0,5767 |
-0,6103 |
-0,6444 |
-0,7141 |
-0,7866 |
-0,8630 |
-0,9443 |
-0,9872 |
|
-15 (-0,262) |
-0,3365 |
-0,4040 |
-0,4380 |
-0,4722 |
-0,5068 |
-0,5418 |
-0,6134 |
-0,6880 |
-0,7665 |
-0,8501 |
-0,8941 |
|
-10 (-0,174) |
-0,2257 |
-0,2946 |
-0,3293 |
-0,3641 |
-0,3994 |
-0,4351 |
-0,5081 |
-0,5842 |
-0,6642 |
-0,7494 |
-0,7943 |
|
-5 (-0,0873) |
-0,1133 |
-0,1830 |
-0,2180 |
-0,2533 |
-0,2890 |
-0,3251 |
-0,3990 |
-0,4759 |
-0,5568 |
-0,6430 |
-0,6885 |
|
0 (0) |
0,0000 |
-0,0699 |
-0,1051 |
-0,1405 |
-0,1763 |
-0,2126 |
-0,2867 |
-0,3640 |
-0,4452 |
-0,5317 |
-0,5774 |
|
5 (0,0873) |
0,1133 |
0,0436 |
0,0086 |
-0,0267 |
-0,0624 |
-0,0984 |
-0,1724 |
-0,2493 |
-0,3302 |
-0,4164 |
-0,4619 |
|
10 (0,174) |
0,2257 |
0,1569 |
0,1222 |
0,0873 |
6,0521 |
0,0164 |
-0,0566 |
-0,1327 |
-0,2127 |
-0,2979 |
-0,3428 |
|
15 (0,262) |
0,3365 |
0,2689 |
0,2349 |
0,2007 |
0,1661 |
0,1312 |
0,0595 |
-0,0151 |
-0,0936 |
-0,1771 |
-0,2212 |
|
20 (0,349) |
0,4446 |
0,3789 |
0,3459 |
0,3126 |
0,2789 |
0,2449 |
0,1752 |
0,1026 |
0,0262 |
-0,0550 |
-0,0979 |
|
25 (0,436) |
0,5494 |
0,4860 |
0,4541 |
0,4220 |
0,3896 |
0,3568 |
0,2895 |
0,2195 |
0,1459 |
0,0675 |
0,0261 |
|
30 (0,524) |
0,6500 |
0,5894 |
0,5590 |
0,5283 |
0,4973 |
0,4659 |
0,4017 |
0,3348 |
0,2644 |
0,1895 |
0,1500 |
|
35 (0,611) |
0,7456 |
0,6884 |
0,6596 |
0,6305 |
0,6012 |
0,5715 |
0,5108 |
0,4475 |
0,3809 |
0,3101 |
0,2727 |
|
40 (0,698) |
0,8356 |
0,7821 |
0,7551 |
0,7280 |
0,7005 |
0,6728 |
0,6160 |
0,5568 |
0,4946 |
0,4283 |
0,3933 |
|
45 (0,785) |
0,9192 |
0,8698 |
0,8449 |
0,8199 |
0,7946 |
0,7689 |
0,7165 |
0,6619 |
0,6044 |
0,5433 |
0,5110 |
|
50 (0,873) |
0,9959 |
0,9509 |
0,9283 |
0,9055 |
0,8825 |
0,8592 |
0,8115 |
0,7619 |
0,7097 |
0,6541 |
0,6247 |
|
55 (0,960) |
1,0649 |
1,0248 |
1,0046 |
0,9843 |
0,9638 |
0,9430 |
0,9004 |
0,8561 |
0,8095 |
0,7599 |
0,7337 |
|
60 (1,050) |
1,1258 |
1,0909 |
1,0733 |
1,0556 |
1,0377 |
1,0196 |
0,9825 |
0,9438 |
0,9032 |
0,8600 |
0,8372 |
|
65 (1,138) |
1,1782 |
1,1486 |
1,1338 |
1,1188 |
1,1037 |
1,0884 |
1,0570 |
1,0244 |
0,9900 |
0,9535 |
0,9342 |
|
70 (1,225) |
1,2216 |
1,1977 |
1,1857 |
1,1735 |
1,1613 |
1,1489 |
1,1235 |
1,0971 |
1,0693 |
1,0397 |
1,0241 |
|
75 (1,312) |
1,2557 |
1,2376 |
1,2285 |
1,2193 |
1,2101 |
1,2007 |
1,1815 |
1,1615 |
1,1405 |
1,1181 |
1,1063 |
|
80 (1,400) |
1,2803 |
1,2681 |
1,2620 |
1,2558 |
1,2496 |
1,2433 |
1,2305 |
1,2170 |
1,2029 |
1,1879 |
1,1800 |
|
K у = 1,40 |
|||||||||||
|
-30 (-0,524) |
-0,7000 |
-0,7606 |
-0,7910 |
-0,8217 |
-0,8527 |
-0,8841 |
-0,9483 |
-1,0152 |
-1,0856 |
-1,1605 |
-1,2000 |
|
-25 (-0,436) |
-0,5917 |
-0,6550 |
-0,6869 |
-0,7190 |
-0,7515 |
-0,7843 |
-0,8515 |
-0,9215 |
-0,9952 |
-1,0736 |
-1,1149 |
|
-20 (-0,349) |
-0,4788 |
-0,5445 |
-0,5776 |
-0,6109 |
-0,6445 |
-0,6786 |
-0,7483 |
-0,8208 |
-0,8972 |
-0,9735 |
-1,0214 |
|
-15 (-0,262) |
-0,3623 |
-0,4299 |
-0,4639 |
-0,4981 |
-0,5327 |
-0,5677 |
-0,6393 |
-0,7139 |
-0,7924 |
-0,8759 |
-0,9200 |
|
-10 (-0,174) |
-0,2431 |
-0,3120 |
-0,3466 |
-0,3815 |
-0,4168 |
-0,4524 |
-0,5255 |
-0,6015 |
-0,6816 |
-0,7667 |
-0,8117 |
|
-5 (-0,0873) |
-0,1220 |
-0,1917 |
-0,2267 |
-0,2620 |
-0,2977 |
-0,3338 |
-0,4077 |
-0,4846 |
-0,5656 |
-0,6517 |
-0,6972 |
|
0 (0) |
0,0000 |
-0,0699 |
-0,1051 |
-0,1405 |
-0,1763 |
-0,2126 |
-0,2867 |
-0,3640 |
-0,4452 |
-0,5317 |
-0,5774 |
|
5 (0,0873) |
0,1220- |
0,0524 |
0,0173 |
-0,0180 |
-0,0536 |
-0,0897 |
-0,1636 |
-0,2406 |
-0,3215 |
-0,4077 |
-0,4531 |
|
10 (0,174) |
0,2431 |
0,1742 |
0,1396 |
0,1047 |
0,0695 |
0,0338 |
-0,0393 |
-0,1153 |
-0,1954 |
-0,2805 |
-0,3255 |
|
15 (0,262) |
0,3623 |
0,2948 |
0,2608 |
0,226 |
0,1920 |
0,1570 |
0,0854 |
0,0108 |
-0,0677 |
-0,1512 |
-0,1953 |
|
20 (0,349) |
0,4788 |
0,4131 |
0,3801 |
0,3468 |
0,3131 |
0,2791 |
0,2094 |
0,1368 |
0,0605 |
-0,0208 |
-0,0637 |
|
25 (0,436) |
0,5917 |
0,5283 |
0,4964 |
0,4643 |
0,4319 |
0,3990 |
0,3318 |
0,2618 |
0,1882 |
0,1098 |
0,0684 |
|
30 (0,524) |
0,7000 |
0,6394 |
0,6090 |
0,5783 |
0,5473 |
0,5159 |
0,4517 |
0,3848 |
0,3144 |
0,2395 |
0,2000 |
|
35 (0,611) |
0,8030 |
0,7457 |
0,7169 |
0,6879 |
0,6586 |
0,6289 |
0,5681 |
0,5049 |
0,4383 |
0,3675 |
0,3301 |
|
40 (0,698) |
0,8999 |
0,8463 |
0,8194 |
0,7922 |
0,7648 |
0,7371 |
0,6802 |
0,6211 |
0,5588 |
0,4926 |
0,4576 |
|
45 (0,785) |
0,9899 |
0,9405 |
0,9156 |
0,8906 |
0,8653 |
0,8396 |
0,7872 |
0,7326 |
0,6751 |
0,6140 |
0,5817 |
|
50 (0,873) |
1,0725 |
1,0275 |
1,0049 |
0,9821 |
0,9591 |
0,9358 |
0,8881 |
0,8385 |
0,7863 |
0,7307 |
0,7013 |
|
55 (0,960) |
1,1468 |
1,1067 |
1,0865 |
1,0662 |
1,0457 |
1,0249 |
0,9823 |
0,9380 |
0,8914 |
0,8418 |
0,8157 |
|
60 (1,050) |
1,2124 |
1,1775 |
1,1599 |
1,1422 |
1,1243 |
1,1062 |
1,0691 |
1,0305 |
0,9898 |
0,9466 |
0,9238 |
|
65 (1,138) |
1,2688 |
1,2393 |
1,2244 |
1,2094 |
1,1943 |
1,1790 |
1,1476 |
1,1150 |
1,0807 |
1,0441 |
1,0248 |
|
70 (1,225) |
1,3156 |
1,2917 |
1,2796 |
1,2675 |
1,2553 |
1,2429 |
1,2175 |
1,1911 |
1,1633 |
1,1337 |
1,1181 |
|
75 (1,312) |
1,3523 |
1,3342 |
1,3251 |
1,3159 |
1,3067 |
1,2973 |
1,2781 |
1,2581 |
1,2371 |
1,2147 |
1,2029 |
|
80 (1,400) |
1,3787 |
1,3666 |
1,3605 |
1,3543 |
1,3481 |
1,3418 |
1,3289 |
1,3155 |
1,3014 |
1,2864 |
1,2785 |
Таблица 2
Значения c oi = ci /( h ср. i cos αi ) , кН/м3
|
αi , град (рад) |
C oi при значениях ci/ hср. i в кН/м3 |
||||||||||
|
0,00 |
5,00 |
10,00 |
15,00 |
20,00 |
25,00 |
30,00 |
35,00 |
40,00 |
45,00 |
50,00 |
|
|
0 (0) |
0,0000 |
5,0000 |
10,0000 |
15,0000 |
20,0000 |
25,0000 |
30,0000 |
35,0000 |
40,0000 |
45,0000 |
50,0000 |
|
5 (0,0873) |
0,0000 |
5,0191 |
10,0382 |
15,0573 |
20,0764 |
25,0955 |
30,1146 |
35,1337 |
40,1528 |
45,1719 |
50,1910 |
|
10 (0,174) |
0,0000 |
5,0771 |
10,1543 |
15,2314 |
20,3085 |
25,3857 |
30,4628 |
35,5399 |
40,6171 |
45,6942 |
50,7713 |
|
15 (0,262) |
0,0000 |
5,1764 |
10,3528 |
15,5291 |
20,7055 |
25,8819 |
31,0583 |
36,2347 |
41,4110 |
46,5874 |
51,7638 |
|
20 (0,349) |
0,0000 |
5,3209 |
10,6418 |
15,9627 |
21,2836 |
26,6044 |
31,9253 |
37,2462 |
42,5671 |
47,8880 |
53,2089 |
|
25 (0,436) |
0,0000 |
5,5169 |
11,0338 |
16,5507 |
22,0676 |
27,5844 |
33,1013 |
38,6182 |
44,1351 |
49,6520 |
55,1689 |
|
30 (0,524) |
0,0000 |
5,7735 |
11,5470 |
17,3205 |
23,0940 |
28,8675 |
34,6410 |
40,4145 |
46,1880 |
51,9615 |
57,7350 |
|
35 (0,611) |
0,0000 |
6,1039 |
12,2077 |
18,3116 |
24,4155 |
30,5194 |
36,6232 |
42,7271 |
48,8310 |
54,9349 |
61,0387 |
|
40 (0,698) |
0,0000 |
6,5270 |
13,0541 |
19,5811 |
26,1081 |
32,6352 |
39,1622 |
45,6893 |
52,2163 |
58,7433 |
65,2704 |
|
45 (0,785) |
0,0000 |
7,0711 |
14,1421 |
21,2132 |
28,2843 |
35,3553 |
42,4264 |
49,4975 |
56,5685 |
63,6396 |
70,7107 |
|
50 (0,873) |
0,0000 |
7,7786 |
15,5572 |
23,3359 |
31,1145 |
38,8931 |
46,6717 |
54,4503 |
62,2290 |
70,0076 |
77,7862 |
|
55 (0,960) |
0,0000 |
8,7172 |
17,4345 |
26,1517 |
34,8689 |
43,5862 |
52,3034 |
61,0206 |
69,7379 |
78,4551 |
87,1723 |
|
60 (1,050) |
0,0000 |
10,0000 |
20,0000 |
30,0000 |
40,0000 |
50,0000 |
60,0000 |
70,0000 |
80,0000 |
90,0000 |
100,0000 |
|
65 (1,138) |
0,0000 |
11,8310 |
23,6620 |
35,4930 |
47,3240 |
59,1550 |
70,9860 |
82,8171 |
94,6481 |
106,4790 |
118,3100 |
|
70 (1,225) |
0,0000 |
14,6190 |
29,2380 |
43,8571 |
58,4761 |
73,0951 |
87,7141 |
102,3331 |
116,9521 |
131,5712 |
146,1902 |
|
75 (1,312) |
0,0000 |
19,3185 |
38,6370 |
57,9556 |
77,2741 |
96,5926 |
115,9111 |
135,2296 |
154,5481 |
173,8666 |
193,1851 |
|
80 (1,400) |
0,0000 |
28,7939 |
57,5877 |
86,3816 |
115,1754 |
143,9692 |
172,7631 |
201,5569 |
230,3508 |
259,1447 |
287,9385 |
|
Примечание . Для получения c oi в единицах тс/м3 значения из табл. 2 следует уменьшить в 10 раз (1 тс/м3 = 10 кН/м3). |
|||||||||||
Таблица 3
Значения λi = cos φ i / cos ( αi - φi )
|
αi , град (рад) |
λi при φ i в град (рад) |
||||||||||
|
0 (0) |
4 (0,0698) |
6 (0,105) |
8 (0,140) |
10 (0,174) |
12 (0,209) |
16 (0,279) |
20 (0,349) |
24 (0,419) |
28 (0,489) |
30 (0,524) |
|
|
-30 (-0,524) |
1,1547 |
1,2033 |
1,2293 |
1,2567 |
1,2856 |
1,3162 |
1,3838 |
1,4619 |
1,5542 |
1,6662 |
1,7321 |
|
-25 (-0,436) |
1,1034 |
1,1406 |
1,1602 |
1,1808 |
1,2022 |
1,2248 |
1,2737 |
1,3289 |
1,3925 |
1,4671 |
1,5099 |
|
-20 (-0,349) |
1,0642 |
1,0920 |
1,1065 |
1,1215 |
1,1372 |
1,1534 |
1,1882 |
1,2267 |
1,2700 |
1,3195 |
1,3473 |
|
-15 (-0,262) |
1,0353 |
1,0550 |
1,0653 |
1,0758 |
1,0866 |
1,0978 |
1,1214 |
1,1472 |
1,1755 |
1,2073 |
1,2247 |
|
-10 (-0,174) |
1,0154 |
1,0281 |
1,0346 |
1,0412 |
1,0480 |
1,0550 |
1,0695 |
1,0851 |
1,1019 |
1,1205 |
1,1305 |
|
-5 (-0,0873) |
1,0038 |
1,0100 |
1,0131 |
1,0163 |
1,0195 |
1,0228 |
1,0297 |
1,0368 |
1,0445 |
1,0528 |
1,0572 |
|
0 (0) |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
1,0000 |
|
5 (0,0873) |
1,0038 |
0,9977 |
0,9974 |
0,9916 |
0,9886 |
0,9855 |
0,9793 |
0,9728 |
0,9662 |
0,9592 |
0,9556 |
|
10 (0,174) |
1,0154 |
1,0031 |
0,9970 |
0,9909 |
0,9848 |
0,9787 |
0,9666 |
0,9542 |
0,9415 |
0,9284 |
0,9216 |
|
15 (0,262) |
1,0353 |
1,0162 |
1,0069 |
0,9977 |
0,9886 |
0,9795 |
0,9614 |
0,9433 |
0,9249 |
0,9062 |
0,8966 |
|
20 (0,349) |
1,0642 |
1,0378 |
1,0250 |
1,0124 |
1,0000 |
0,9878 |
0,9636 |
0,9397 |
0,9158 |
0,8916 |
0,8794 |
|
25 (0,436) |
1,1034 |
1,0685 |
1,0518 |
1,0355 |
1,0195 |
1,0039 |
0,9732 |
0,9433 |
0,9137 |
0,8842 |
0,8693 |
|
30 (0,524) |
1,1547 |
1,1099 |
1,0886 |
1,0680 |
1,0480 |
1,0285 |
0,9907 |
0,9542 |
0,9186 |
0,8835 |
0,8660 |
|
35 (0,611) |
1,2208 |
1,1638 |
1,1371 |
1,1114 |
1,0866 |
1,0626 |
1,0167 |
0,9728 |
0,9306 |
0,8896 |
0,8693 |
|
40 (0,698) |
1,3054 |
1,2331 |
1,1996 |
1,1677 |
1,1372 |
1,1078 |
1,0522 |
1,0000 |
0,9504 |
0,9027 |
0,8794 |
|
45 (0,785) |
1,4142 |
1,3218 |
1,2797 |
1,2399 |
1,2022 |
1,1663 |
1,0991 |
1,0368 |
0,9785 |
0,9233 |
0,8966 |
|
50 (0,873) |
1,5557 |
1,4360 |
1,3825 |
1,3325 |
1,2856 |
1,2413 |
1,1595 |
1,0851 |
1,0164 |
0,9523 |
0,9216 |
|
55 (0,960) |
1,7434 |
1,5851 |
1,5159 |
1,4520 |
1,3927 |
1,3374 |
1,2369 |
1,1472 |
1,0658 |
0,9910 |
0,9556 |
|
60 (1,050) |
2,0000 |
1,7839- |
1,6920 |
1,6085 |
1,5321 |
1,4618 |
1,3363 |
1,2267 |
1,1292 |
1,0412 |
1,0000 |
|
65 (1,138) |
2,3662 |
2,0576 |
1,9310 |
1,8182 |
1,7170 |
1,6253 |
1,4652 |
1,3289 |
1,2105 |
1,1056 |
1,0572 |
|
70 (1,225) |
2,9238 |
2,4526 |
2,2687 |
2,1093 |
1,9696 |
1,8458 |
1,6354 |
1,4619 |
1,3151 |
1,1881 |
1,1305 |
|
75 (1,312) |
3,8637 |
3,0641 |
2,7751 |
2,5344 |
2,3303 |
2,1546 |
1,8664 |
1,6383 |
1,4516 |
1,2946 |
1,2247 |
|
80 (1,400) |
5,7588 |
4,1235 |
3,6081 |
3,2046 |
2,8794 |
2,6111 |
2,1928 |
1,8794 |
1,6337 |
1,4341 |
1,3473 |
ЛИТЕРАТУРА
1 . Веселовский Б.В., Дорфман А.Г., Смирнов Д.В., Шевченко М.И. Расчет оползневого давления и устойчивости склона против переползания грунта через подпорную стену. - В сб.: Вопросы геотехники: Тр. /ДИИТ. - Днепропетровск, 1972, № 21.
2 . Вопросы геотехники: Тр. /ДИИТ. - Днепропетровск, 1969, № 14.
3 . Гинзбург Л.К. Расчет оползневого давления с учетом влияния сейсмики и гидродинамической силы. - Транспортное строительство, 1974, № 9.
4 . Гинзбург Л.К. Противооползневые удерживающие конструкции. - М.: Стройиздат, 1979.
5 . Гинзбург Л.К. Методы определения оползневого давления. - Промышленное строительство и инженерные сооружения, 1980, № 3.
6 . Гинзбург Л.К. Величина коэффициента устойчивости склона при расчете удерживающих конструкций. - Промышленное строительство и инженерные сооружения, 1984, № 1.
7 . Гольдштейн М.Н. Исследования устойчивости оползневых масс и способы ее повышения. - В сб.: Борьба с оползнями, обвалами и размывами на ж. д. Кавказа. - М.; 1961.
8 . Гольдштейн М.Н. Вариационный метод решения задач об устойчивости грунтов. - В сб.: Вопросы геотехники: Тр. /ДИИТ. - Киев, 1969, № 16.
9 . Дорфман А.Г. Оползневое давление и выпор грунта. - В сб.: Вопросы геотехники: Тр. /ДИИТ. - Днепропетровск, 1972, № 20.
10 . Инструкция по проектированию и строительству противооползневых и противообвальных защитных сооружений. СН 519-79 /Госстрой СССР. - М.: Стройиздат, 1981.
11 . Карцивадзе Г.Н. Сейсмостойкость дорожных искусственных сооружений. - М: Транспорт, 1974.
12 . Корольков Н.М., Еремин В.Л. Путь и сооружения на горных железных дорогах. - М.: Транспорт, 1968.
13 . Котов М.Ф . Механика грунтов в примерах. - М.: Высшая школа, 1968.
14 . Левин С.В. Механика грунтов. - М.: Недра, 1964.
15 . Маслов Н.Н. Механика грунтов в практике строительства. (Оползни и борьба с ними). - М.: Стройиздат, 1977.
16 . Медков Е.И., Березанцев В.Г., Гольдштейн М.Н., Царьков А.А. Механика грунтов, основания и фундаменты. - М.: Транспорт, 1970.
17 . Оползни и инженерная практика /Под ред. Э.Б. Эккеля: Сокращ. пер. с англ. проф. М.Н. Гольдштейна. - М.: Трансжелдориздат, 1960.
18 . Основания и фундаменты /Под ред. проф. Д.А. Леонардса: Пер. с англ. проф. М.Н. Гольдштейна. - М.: Стройиздат, 1968.
19 . Перковский Л.Л. Элементы расчета устойчивости оползневого массива. - В сб.: Оползни и борьба с ними: Тр. /Сев.-Кавказ. семинара. - Ставрополь, 1964.
20 . СНиП II-7-81 . Строительство в сейсмических районах /Госстрой СССР. - М.: Стройиздат, 1982.
21 . СНиП II-55-79 . Подпорные стены, судоходные шлюзы, рыбопропускные и рыбозащитные сооружения /Госстрой СССР. - М.: Стройиздат, 1980.
22 . Соловьев Ю.И. Устойчивость откосов из гипотетического грунта: Тр. /НИИЖТ. Новосибирск, 1962, вып. XXVIII .
23 . Справочник инженера-путейца /Под ред. В.В. Басилова, М.А. Чернышева. Т. 1. - М.: Транспорт, 1972.
24 . Справочник проектировщика: Сложные основания и фундаменты /Под ред. к. т. н. Ю.Г. Трофименкова. - М.: Стройиздат, 1969.
25 . Тейлор Д. Основы механики грунтов: Пер. с англ. инж. Г.Л. Игнатюка. - М.: Госстройиздат, 1960.
26 . Федоров И.В. Методы расчета устойчивости склонов и откосов. - М.: Госстройиздат, 1962.
27 . Федоров И.В. Учет фильтрационного воздействия при расчете устойчивости земляных откосов. - В сб.: Устойчивость фильтрующих откосов - Минск, 1969.
28 . Харр М.Е. Основы теоретической механики грунтов: Пер. с англ. проф. М.Н. Гольдштейна. - М.: Стройиздат, 1971.
29 . Хоу Б.К. Основы инженерного грунтоведения: Пер. с англ. проф. Н.Н. Маслова. - М.: Стройиздат, 1966.
30 . Цытович Н.А. Механика грунтов. - М.: Высшая школа, 1973.
31 . Чеботарев Г.П. Механика грунтов, основания и земляные сооружения: Пер. с англ. проф. Н.Н. Маслова. - М.: Стройиздат, 1968.
32 . Чугаев Р.Р. Дифференциальные уравнения неустановившегося движения жидкости и фильтрационные силы для общего случая слитно-пористого тела: Известия /ВНИИГ им. Веденеева Б.Е. - Л.: 1965, т. 78.
33 . Чугаев Р.Р. Расчет общей устойчивости откосов земляной плотины с учетом фильтрационных сил. - Гидротехническое строительство, 1965, № 5.
34 . Чугаев Р.Р. Земляные гидротехнические сооружения (теоретические основы расчета). - Л.: Энергия, 1967.
35 . Чугаев Р.Р. Об ошибках, допускаемых некоторыми авторами при замене фильтрационных сил поверхностными силами гидротехнического давления. - В сб.: Устойчивость фильтрующих откосов. - Минск, 1969.
36 . Шабанов А.Д. Крепление напорных земляных откосов. - М.: Стройиздат; 1971.
37 . Шахунянц Г.М. Расчет устойчивости склонов и откосов против скольжения пород. - В кн.: Материалы совещания по вопросам изучения оползней и мер борьбы с ними. - Киев, изд-во Киевского ун-та, 1964.
38 . Шахунянц Г.М. К вопросу выбора рациональных методов расчета склонов. - В сб.: Оползни и борьба с ними: Тр. /Сев.-Кавказ. семинара. - Ставрополь, 1964.
39 . Шахунянц Г.М. Железнодорожный путь. - М.: Транспорт, 1969.
40 . Ясюнас Л.П. Вопросы борьбы с оползнями на железных дорогах. - М.: Трансжелдориздат, 1949.
СОДЕРЖАНИЕ
|
Условные обозначения . 1 Предисловие . 2 I. Исходные положения . 3 1.1. Основные предпосылки . 3 1.2. Учет действия грунтовых вод . 6 1.3. Учет сейсмических воздействий . 11 II. Методы расчета . 13 2.1. Метод круглоцилиндрической поверхности скольжения . 13 2.2. Метод Ю.И. Соловьева . 15 2.3. Метод Fр 18 2.4. Метод Р.Р. Чугаева . 20 2.5. Метод горизонтальных сил . 28 2.6. Метод касательных сил . 31 2.7. Аналитический метод Г.М. Шахунянца . 34 2.8. Графоаналитический метод многоугольников сил Г.М. Шахунянца . 39 2.9. Ускоренный способ расчета методом Г.М. Шахунянца . 42 2.10. Графостатический метод Л.Л. Перковского . 49 2.11. Метод блока и призм .. 50 2.12. Метод Л.П. Ясюнас . 51 2.13. Метод ДИИТа . 54 2.14. Определение давления от призмы обрушения по теории Кулона . 60 III. Анализ и выводы .. 62 3.1. Сравнение методов расчета . 62 3.2. Рекомендации по применению .. 68 3.3. Принципы построения эпюры оползневого давления . 69 Заключение . 74 Приложение. Таблицы для расчета оползневого давления ускоренным способом .. 76 Литература . 83 |