Р 50.1.040-2002 Статистические методы. Планирование экспериментов. Термины и определения
Р 50 .1 .040 -2002
РЕКОМЕНДАЦИИ ПО СТАНДАРТИЗАЦИИ
Статистические методы
ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТОВ
Термины и определения
ГОССТАНДАРТ РОССИИ
Мо сква
Предисловие
1 РАЗРАБОТАНЫ И ВНЕСЕНЫ Техническим комитетом по стандартизации ТК 125 «Статистические методы в управлении качеством продукции»;
Акционерным обществом «Научно-исследовательский центр контроля и диагностики технических систем» (АО «НИЦ КД» )
2 ПРИНЯТЫ И ВВЕДЕНЫ В ДЕЙСТВИЕ Постановлением Госстандарта России от 2 октября 2002 г. № 362 -ст
3 Настоящие Рекомендации по стандартизации, за исключением разделов 1а , 1б и приложения А, представляют собой аутентичный текст международного стандарта И СО 3534 -3-99 «Статистика. Словарь и условные обозначения. Часть 3 . Планирование экспериментов»
4 ВВЕДЕНЫ ВПЕРВЫЕ
СОДЕРЖАНИЕ
|
1а Область применения . 2 1б Нормативные ссылки . 2 1 Общие термины .. 2 2 Расположения экспериментов . 4 3 Методы анализа . 7 Алфавитный указатель терминов на русском языке . 7 Алфавитный указатель терминов на английском языке . 9 Алфавитный указатель терминов на французском языке . 11 Приложение А. Пояснения и примеры к терминам, приведенным в настоящих рекомендациях . 12 |
Введение
Установленные в настоящих рекомендациях термины расположены в систематизированном порядке и отражают систему понятий в области планирования экспериментов.
Для каждого понятия установлен один стандартизованный термин.
Недопустимые термины-синонимы, набранные курсивом, приведены в круглых скобках после стандартизованного термина и обозначены пометой «Ндп .».
Термины-синонимы, набранные курсивом, но без пометы «Ндп.» приведены в качестве справочных данных и не являются стандартизованными.
Заключенная в круглые скобки часть термина может быть опущена при использовании термина в документах по стандартизации.
Наличие квадратных скобок в терминологической статье означает, что в нее включены два термина, имеющие общие термоэлементы. В алфавитных указателях данные термины приведены отдельно с указанием номера статьи.
Приведенные определения можно при необходимости изменять, вводя в них производные признаки , раскрывая значения используемых в них терминов, указывая объекты, входящие в объем определяемого понятия. Изменения не должны нарушать объем и содержание понятий, определенных в данных рекомендациях.
В рекомендациях приведены иноязы ч ные эквиваленты стандартизованных терминов на английском ( en ) и французском ( fr ) языках.
Стандартизованные термины набраны полужирным шрифтом, их краткие формы - светлым.
Приложение А содержит пояснения и примеры к терминам, установленным настоящими рекомендациям и.
Р 50.1.040-2002
РЕКОМЕНДАЦИИ ПО СТАНДАРТИЗАЦИИ
Статистические методы
ПЛАНИРОВАНИЕ ЭКСПЕРИМЕНТОВ
Термины и определения
Statistical methods .
Design of experiments . Terms and definitions
Дата введения 2003-07-01
1а Область применения
Настоящие рекомендации устана в ливают термины и определения понятий в области математической статистики по планированию экспериментов.
Термины, установленные настоящими рекомендациями, обязательны для применения во всех видах документации и литературы по планированию экспериментов, входящих в сферу работ по стандартизации и( ил и) использующих результаты этих работ.
1б Нормативные ссылки
В настоящих рекомендациях использованы ссылки на следующие стандарты:
ГОСТ Р 50779.10-2000 (ИСО 3534 -1-93 ) Статистические методы. Вероятность и основы статистики. Термины и определения
ГОСТ Р 50779.11-2000 (ИСО 3534 -2-93 ) Статистические методы. Статистическое управление качеством. Термины и определения
1 Общие термины
1.1 модель en model
Описание, связывающее отклик с предсказывающей fr mod é le
переменной или предсказывающими переменными и
включающее сопутствующие предположения
1 .2 отклик; выходная переменная (Ндп. зависимая en responze variable
переменная ) fr variable de résponse
Переменная, представляющая результат эксперимента
1 .3 предсказывающая переменная; предиктор ; en predictor variable
входная переменная (Ндп. независимая переменная.) fr variable de prédiction
Переменная, которая может помочь объяснить результат
эксперимента
1 .4 пространство планирования; область планирования en design region ;
Множество допустимых значений предсказывающей design space
переменной fr zone du plan espace
du plan
1 .5 фактор en factor
Предсказывающая переменная, варьируемая с целью fr facteur
определения ее влияния на отклик
1 .6 уровень (фактора) en level
Потенциальная установка, значение или назначение фактора fr niveau
1.7 ошибка опыта; ошибка эксперимента en experimental error
Вариация в откликах, которая не обусловлена факторами, fr erreur exp é rimentale
блоками или известными источниками в ходе проведения
эксперимента
1 .8 компонента дисперсии en variance component
Дисперсия случайной величины, описывающей эффект fr composante de variance
фактора или ошибку опыта
1 .9 экспериментальная единица en experimental unit
Объект, подвергаемый обработке, вследствие чего получают fr unit é exp é rimentale
значение отклика
1.10 обработка en treatment
Конкретная комбинация уровней всех факторов fr traitement
1.11 блок (плана) en block
Множество экспериментальных единиц, более однородных, fr bloc
чем все множество экспериментальных единиц
1.12 о дн офакторны й эксперимент en one -factor experiment
Эксперимент, в котором изучают влияние на отклик, если fr exp é rience á un facteur
оно есть, одного фактора
1 .13 главный эффект (фактора) en main effect
Влияние отдельного фактора на среднее значение отклика fr effet principal
1.14 эффект рассеивания en dispersion effect
Влияние отдельного фактора на дисперсию отклика fr effet de dispersion
1.15 дв у хфакторны й эксперимент en two -factor experiment
Эксперимент, в котором два разных фактора исследуют fr exp é rience á deux
одновременно для определения их влияния на отклик facteurs
1 .16 k -факторн ы й эксперимент ; многофакторный en k - factor experiment
эксперимент fr expérience á k facteurs
Эксперимент, в котором k ≥ 2 разных факторов изучают
одновременно для определения их влияния на отклик
1 .17 взаимодействие (факторов); дифференциальный en interaction
эффект fr interaction
Ситуаци я, когда проявленное влияние одного фактора на
отклик зависит от других факторов, одного или более
1.18 смешивание (эффектов) en confounding
Намеренное объединение двух и более эффектов - главного fr concomitance
и взаимодействий, так чтобы они были неразличимы
1.19 совместный эффект en alias
Статистический эффект - главный или взаимодействие, fr alise effet ins é parable
который полностью смешивается с другим главным
эффектом или взаимодействием из-за природы эксперимента
1 .20 нелинейность (модели); кривизна en curvature
Отклонение от прямой отношения между откликом и fr courbure
предсказывающей переменной
1 .21 остаток en residual
Разница между наблюдаемым и предсказанным или fr r é sidu
расчетным значениями отклика
1 .22 остаточная ошибка en residual error
Случайная величина, представляющая разность между fr r é siduelle
наблюдаемыми и предсказанными значениями отклика,
полученными на основе постулированной модели
1 .23 чистая ошибка en pure error
Случайная величина, отражающая вариабельность, fr erreur pure
связанную с повторными наблюдениями при фиксированной
обработке
1 .24 контраст en contrast
Статистическая линейная функция откликов, для которой fr contraste
сумма коэффициентов равна нулю, хотя не все они равны нулю
1 .25 ортогональн ый контраст en orthogonal contrast
Набор контрастов, коэффициенты которых удовлетворяют fr contraste orthogonal
условию, что, если перемножить соответствующие пары,
сумма произведений будет равна нулю
1 .26 ортогональное расположение en orthogonal array
Набор обработок, в котором для каждой пары факторов fr arrangement orthogonal
каждая комбинация обработок появляется одинаковое число
раз на каждом возможном уровне фактора
1 .27 повторение (эксперимента) en replication
Выполнение эксперимента более чем один раз для данного fr r é plique
набора предсказывающих переменных.
Примечание - В настоящих рекомендациях термин «повторение» дан
с точки зрения планирования экспериментов , он объединяет и уточняет
как термин «повторение», так и термин «реплика» по 2 .89 и 2 .90
ГОСТ Р 50779.10
1.28 разбиение на блоки; блокирование en blocking
Расположение экспериментальных единиц в от н осительно fr mise en blocs
однородных блоках таким образом, что внутри каждого
блока ошибку эксперимента предполагают меньшей, чем
можно было бы ожидать, если бы такое же число единиц
было случайно отобрано в данную обрабо т ку
1 .29 рандомизация (плана) en randomization
Процесс, используемый для назначения обработок fr randomisation
экспериментальным единицам таким образом, чтобы для
каждой экспериментальной единицы вероятность назначения
определенной обработки была одинаковой
Примечание - Более общее определение к термину «рандомизация»
дано в 2 .91 ГОСТ Р 50779. 10
1 .30 план эксперимента en experimental plan
Назначение обработок каждой экспериментальной единице fr plan d ' exp é rience
и порядка их выполнения
1 .31 спланированный эксперимент en designed experiment
План эксперимента, выбранный для достижения fr exp é rience planifi é e
определенной цели
1 .32 эволюционное планирование; ЭВОП en evolutionary operation ,
Последовательная форма проведения EVOP
экспериментирования на промышленном оборудовании fr exp é rimentation
в ходе нормальной работы производства é volutive , EVOP
1 .33 полностью рандомизированный план en completely randomized
План, в котором обработки назначают случайным design
образом для всего множества экспериментальных единиц fr plan compl é tement
randomise
1 .34 точка (плана) в вершине куба en cube point
Вектор заданных уровней факторов в виде ( а 1 , а2 , …, ak ) , fr point cubique
где каждое ai равно плюс 1 или минус 1, что означает
кодированные уровни факторов; где i = 1, …, k
1 .35 звездная точка (плана) en star point
Вектор заданных уровней факторов в виде ( а 1 , а2 , …, an ) , fr point é toile
где одно ai равно плюс α или минус α , а другие ai равны 0 ,
где α , минус α и 0 означают кодированные уровни факторов;
где i = 1, …, n
1 .36 центральная точка (плана) en centre point
Вектор заданных уровней факторов в виде ( а 1 , а2 , …, ak ), fr point central
где каждое ai = 0 , i = 1, …, n , а 0 означает кодированные
уровни факторов
1 .37 ротатабельность (плана) en rotatability
Характеристика плана, в котором отклики, предсказанные fr rotativit é
по подобранной модели, имеют одну и ту же дисперсию на
одинаковых расстояниях от центра плана
2 Расположения экспериментов
2.1 (полный) факторный эксперимент en full factorial
Эксперимент, состоящий из всех возможных обработок, experiment ; factorial
образованных двумя или более факторами, каждый из experiment
которых изучают на двух или более уровнях fr plan factoriel
complet ; plan factoriel
2 .1 .1 дробный факторный эксперимент en fractional factorial
Эксперимент, состоящий из подмножества полного experiment
факторного эксперимента fr plan factoriel fractionn é
2.1 .2 двухуровневый факторный эксперимент en two - level experiment
Факторный эксперимент, в котором все факторы варьируют fr plan á deux niveaux
на двух уровнях
2 .1.2.1 факторный эксперимент 2 k en 2 k factorial experiment
Факторный эксперимент, в котором изучают k факторов, fr plan factoriel 2 k
каждый на двух уровнях
2 .1 .2 .2 дробный факторный эксперимент 2 ( k - p ) ; en 2 k - p fractional factorial
дробная реплика experiment
Факторный эксперимент, использующий тщательно fr plan factoriel fractionn é
отобранное подмножество ( 2 k - p ) полного факторного 2 k - p
эксперимента 2 k , где k - число факторов полного
факторного эксперимента; p - число факторов
подмножества полного факторного эксперимента
2.1 .3 разрешающая способность плана en design resolution
Длина минимальной строки символов в генерирующем fr r é solution de plan
соотношении
2 .2 план отсеивания en screening design
Эксперимент, направленный на выявление подмножества fr plan de « screening »
из совокупности факторов для дальнейшего изучения
2.3 блочный план en block design
План эксперимента, который использует преимущества fr plan en blocs
однородности подмножеств из множества
экспериментальных единиц
2 .3.1 рандомизированный блочный план en randomized block
План эксперимента, состоящий из n блоков с p обработками, design
которые назначены внутри каждого блока случайным fr plan en blocs
образом randomisés
2 .3 .2 план « латинский квадрат » en latin square design
План с тремя факторами, каждый из которых имеет h fr plan en carr é latin
уровней, в котором комбинация уровней одного из
факторов с уровнями двух других факторов появляется
лишь однажды в эксперименте объема h 2
2 .3 .3 план греко-латинского квадрата en Graeco - Latin square
План, включающий 4 фактора, каждый из которых design
имеет h уровней, в котором комбинация уровней одного fr plan en carr é gr é co - latin
фактора с уровнями других трех факторов появляется
только однажды в эксперименте объема h 2
2 .3 .4 непол н облочны й план en incomplete block
План, в котором экспериментальные единицы design
разделены на блоки, которые недостаточны для проведения fr plan en blocs
полного набора обработок эксперимента incomplets
2 .3 .4 .1 сбалансированный неполн облочны й план en balanced incomplete
Неполноблочн ы й план, в котором каждый блок block design BIBD
содержит одинаковое число k различных уровней из fr plan en blocs
l уровней главного фактора, расположенных так, что каждая incomplets é quilibr é s
пара уровней встречается в λ , блоках из b блоков PBIE
2 .3 .4 .2 частично сбалансированный неполноблочный en partially balanced
план incomplete block design
Неполноблочный план, в котором каждый блок содержит PBIB
одинаковое число различных уровней k из l уровней fr plan en blocs
главного фактора, расположенных так, что не все пары incomplets partiellement
уровней появляются вместе в одинаковом числе блоков b é quilibr é s BIPE
2.3 .5 квадрат Юдена en Youden square
Блочный план, получаемый из латинского квадрата fr carr é de Youden
удалением или добавлением строк или столбцов таким
образом, чтобы получить рандомизированный блочный план
по отношению к одному блоковому фактору и неполноблочн ы й
план по отношению к другому
2.3 .6 план с расщепленной делянкой en split - plot design
План, в котором группа экспериментальных единиц или fr plan en parcelles
делянка с одним и тем же вариантом главного фактора subdivis é es
расщеплена таким образом, что внутри каждого варианта
этого фактора можно исследовать еще дополнительные
главные факторы
2 .3 .7 д ву хфакторный план с расщеп ленной делянкой ; en two - way split - plot
план с расщепленным блоком design ; split - block design
План с делянкой, расщепленной двумя разными fr plan en blocs
способами, в котором варианты фактора второго subdivis é es
этапа вместо независимой рандомизации внутри каждой
делянки расположены полосами, пересекающими делянки
в каждом повторении
2 .4 план поверхности отклика en response surface design
План, направленный на изучение функциональной fr plan á surface de
зависимости между откликом и набором предсказывающих r é ponse
переменных
2.5 план для смесей en mixture design
План, созданный для случая, когда на сумму fr plan pour l 'é tude
предсказывающих переменных наложено ограничение, de m é langes
требующее ее постоянства
2 .6 (гнездовой) э ксперимент с группировкой ; en nested design
иерархический эксперимент fr plan embo î t é
План эксперимента, в котором каждый уровень данного
фактора появляется только с одним уровнем любого другого
фактора
2 .6 .1 сбалансированный (гнездовой) эксперимент с en balanced nested design ;
группировкой ; полностью сгруппированный эксперимент fully nested design
Эксперимент, в котором число уровней факторов на fr plan embo î t é é quilibr é
каждом уровне иерархии одинаково
2 .6 .2 нерегулярный (гнездовой) эксперимент с en staggered nested design
группировкой ; нерегулярный иерархический эксперимент fr plan irr é guli é rement
Эксперимент, в котором второй вложенный фактор имеет embo î t é
два уровня в первом уровне первого фактора эксперимента с
группировкой, но только один уровень во втором уровне
первого фактора эксперимента с группировкой
2.7 оптимальный план en optimal design
План эксперимента, значения уровней факторов которого fr plan optimal
определены таким образом, чтобы оптимизировать
некоторый критерий, обычно какую-то функцию от матрицы
плана
2 .7 .1 матрица плана en design matrix
Матрица оптимального плана со строками, означающими fr matrice de plan
индивидуальные обработки, которые могут быть расширены
выведенными уровнями других функций от уровней
факторов, но зависят от постулированной модели
2 .7.1.1 D - о пти мал ьны й план en D -optimal design
Оптимальный план, максимизирующий определитель fr plan optimal D
матрицы плана
2 .7 .1 .2 А-о птимальный план en A - optimal design
Оптимальный план, максимизирующий след матрицы fr plan optimal A
плана
2 .7 .1 .3 G -о пти мал ьный план en G - optimal design
Оптимальный план , минимизирующий максимальную fr plan optimal G
дисперсию прогноза по всей области эксперимента
2.8 ортогональный план en orthogonal design
План, в котором каждая пара факторов ортогональна fr plan orthogonal
2 .9 насыщенный план en saturated design
План, матрица которого имеет столько же столбцов, fr plan satur é
сколько и обработок в эксперименте
3 Методы анализа
3.1 графический метод en graphical method
Метод анализа, основанный на графическом представлении fr m é thode graphique
результатов эксперимента
3.1.1 график главных эффектов en main effects plot
График, дающий средние отклики на разных уровнях fr trac é des effets
отдельных факторов principaux
3.1 .2 график взаимодействий en interaction plot
График, отображающий средние отклики на уровнях двух fr trac é d ' interaction
различных факторов
3 .1 .3 график квантилей эффектов en quantile plot of effects
График квантилей стандартного нормального закона fr trac é quantile des effets
распределения для оценок эффектов полного или дробного
факторного эксперимента
3.1 .4 график остатков en method of lest squares
График зависимости остатков от соответствующих fr trac é r é siduel
значений предсказывающих переменных или от уровней
конкретного фактора
3 .2 метод наименьших квадратов en residual plot
Метод оценки параметров, минимизирующий сумму fr m é thodedes moondres
квадратов ошибок, причем ошибку определяют как carr é s
разность между наблюдаемым значением и значением,
вычисленным исходя из постулированной модели, а сумму
берут по всем обработкам
3 .3 регрессионный анализ en regression analysis
Набор процедур, связанных с оцениванием моделей fr analyse de r é gression
зависимости отклика от предсказывающих переменных
3 .4 дисперсионный анализ en analysis of variance
Метод, который разделяет общую вариацию набора fr analyse de variance
данных на имеющие смысл компоненты, связанные
с конкретными источниками вариации
3 .4.1 модель дисперсионного анализа с постоянными en fixed effects
эффектами analysis of variance
Дисперсионный анализ, в котором уровни каждого fr analyse de variance
фактора выбраны заранее из множества значений á effets fix é s
факторов
3 .4 .2 модель дисперсионного анализа со случайными en random effects
эффектами analysis of variance
Дисперсионный анализ, в котором уровни каждого fr analyse de variance
фактора, как предполагается, выбраны случайным á effets al é atoires
образом из совокупности уровней этих факторов
3 .4 .3 смешанная модель дисперсионного анализа en mixed model
Дисперсионный анализ, в котором уровни некоторых analysis of variance
факторов постоянны, а для остальных - их выбирают fr analyse de variance
случайно из совокупности уровней факторов de mod é le mixte
3 .5 ковариационный анализ en analysis of covariance
Метод оценивания и испытания эффектов обработок, fr analyse de covariance
когда сопутствующие факторы влияют на отклик
АЛФАВИТНЫЙ УКАЗАТЕЛЬ ТЕРМИНОВ НА РУССКОМ ЯЗЫКЕ
анализ дисперсионный 3.4
анализ ковариационный 3.5
анализ регрессионный 3.3
блок (плана) 1.11
блокирование 1.28
взаимодействие (факторов) 1.17
график взаимодействий 3.1.2
график главных эффектов 3.1.1
график квантилей эффектов 3.1.3
график остатков 3.1.4
единица экспериментальная 1.9
квадрат Юдена 2.3.5
компонента дисперсии 1.8
контраст 1.24
контраст ортогональный 1.25
кривизна 1.20
матрица плана 2.7.1
метод графический 3.1
метод наименьших квадратов 3.2
модель 1.1
модель дисперсионного анализа с постоянными эффектами 3.4.1
модель дисперсионного анализа со случайными эффектами 3.4.2
модель дисперсионного анализа смешанная 3.4.3
нелинейность (модели) 1.20
область планирования 1.4
обработка 1.10
остаток 1.21
отклик 1.2
ошибка опыта 1.7
ошибка остаточная 1.22
ошибка чистая 1.23
ошибка эксперимента 1.7
переменная входная 1.3
переменная выходная 1.2
переменная зависимая (Нд) 1.2
переменная независимая (Нд) 1.3
переменная предсказывающая 1.3
план блочный 2.3
план греко-латинского квадрата 2.3.3
план для смесей 2.5
план «латинский квадрат» 2.3.2
план насыщенный 2.9
план неполноблочный 2.3.4
план неполноблочный сбалансированный 2.3.4.1
план неполноблочный частично сбалансированный 2.3.4.2
план оптимальный 2.7
план оптимальный А 2.7.1.2
план оптимальный D 2.7.1.1
план оптимальный G 2.7.1.3
план ортогональный 2.8
план отсеивания 2.2
план поверхности отклика 2.4
план полностью рандомизированный 1.33
план рандомизированный блочный 2.3.1
план с расщепленным блоком 2.3.7
план с расщепленной делянкой 2.3.6
план с расщепленной делянкой двухфакторный 2.3.7
план эксперимента 1.30
планирование эволюционное; ЭВОП 1.32
повторение (эксперимента) 1.27
предиктор 1.3
пространство планирования 1.4
разбиение на блоки 1.28
рандомизация (плана) 1.29
расположение ортогональное 1.26
реплика дробная 2.1.2.2
ротатабельность (плана) 1.37
смешивание (эффектов) 1.18
способность плана разрешающая 2.1.3
точка (плана) в вершине куба 1.34
точка (плана) звездная 1.35
точка (плана) центральная 1.36
уровень (фактора) 1.6
фактор 1.5
эксперимент двухфакторный 1.15
эксперимент 2( k - p ) дробный факторный 2.1.2.2
эксперимент (гнездовой) с группировкой 2.6
эксперимент (гнездовой) сбалансированный с группировкой 2.6.1
эксперимент (гнездовой) нерегулярный с группировкой 2.6.2
эксперимент двухуровневый факторный 2.1.2
эксперимент дробный факторный 2.1.1
эксперимент иерархический 2.6
эксперимент иерархический нерегулярный 2.6.2
эксперимент многофакторный 1.16
эксперимент однофакторный 1.12
эксперимент (полный) факторный 2.1
эксперимент полностью сгруппированный 2.6.1
эксперимент спланированный 1.31
эксперимент k -факторный 1.16
эксперимент 2 k -факторный 2.1.2.1
эффект (фактора) главный 1.13
эффект дифференциальный 1.17
эффект рассеивания 1.14
эффект совместный 1.19
АЛФАВИТНЫЙ УКАЗАТЕЛЬ ТЕРМИНОВ НА АНГЛИЙСКОМ ЯЗЫКЕ
A-optimal design 2.7.1.2
alias 1.19
analysis of covariance 3.5
analysis of variance 3.4
balanced incomplete block design 2.3.4.1
balanced nested design 2.6.1
block 1.11
block design 2.3
blocking 1.28
centre point 1.36
completely randomized design 1.33
confounding 1.18
contrast 1.24
cube point 1.34
curvature 1.20
D-optimal design 2.7.1.1
design matrix 2.7.1
design region 1.4
design resolution 2.1.3
design space 1.4
designed experiment 1.31
dispersion effect 1.14
evolutionary operation 1.32
experimental error 1.7
experimental plan 1.30
experimental unit 1.9
k -factor experiment 1.16
2k factorial experiment 2.1.2.1
2k -p fractional factorial experiment 2.1.2.2
factor 1.5
factorial experiment 2.1
fractional factorial experiment 2.1.1
full factorial experiment 2.1
fully nested design 2.6.1
G-optimal design 2.7.1.3
Graeco-Latin square design 2.3.3
graphical method 3.1
hierarchical design 2.6
incomplete block design 2.3.4
interaction 1.17
interaction plot 3.1.2
latin square design 2.3.2
level 1.6
main effect 1.13
main effects plot 3.1.1
method of least squares 3.2
mixture design 2.5
model 1.1
model 1 analysis of variance 3.4.1
model 2 analysis of variance 3.4.2
model 3 analysis of variance 3.4.3
nested design 2.6
one-factor experiment 1.12
optimal design 2.7
orthogonal array 1.26
orthogonal contrast 1.25
orthogonal design 2.8
partially balanced incomplete block design 2.3.4.2
predictor variable 1.3
pure error 1.23
quantile plot of effects 3.1.3
randomization 1.29
randomized block design 2.3.1
regression analysis 3.3
replication 1.27
residual 1.21
residual error 1.22
residual plot 3.1.4
response surface design 2.4
responze variable 1.2
rotatability 1.37
saturated design 2.9
screening design 2.2
split-block design 2.3.7
split-plot design 2.3.6
staggered nested design 2.6.2
star point 1.35
treatment 1.10
two-factor experiment 1.15
two-level experiment 2.1.2
two-way split-plot design 2.3.7
variance component 1.8
Youden square 2.3.5
АЛФАВИТНЫЙ УКАЗАТЕЛЬ ТЕРМИНОВ НА ФРАНЦУЗСКОМ ЯЗЫКЕ
aliase 1.19
analyse de covariance 3.5
analyse de regression 3.3
analyse de variance 3.4
analyse de variance de modéle 1 3.4.1
analyse de variance de modéle 2 3.4.2
analyse de variance de modéle 3 3.4.3
arrangement orthogonal 1.26
bloc 1.11
carré de Youden 2.3.5
composante de variance 1.8
concomitance 1.18
contraste 1.24
contraste orthogonal 1.25
courbure 1.20
effet de dispersion 1.14
effet inséparable 1.19
effet principal 1.13
erreur expérimentale 1.7
erreur pure 1.23
erreur résiduelle 1.22
espace du plan 1.4
expérience a deux facteurs 1.15
expérience a k facteurs 1.16
expérience a un facteur 1.12
expérience planifiée 1.31
expérimentation évolutive 1.32
facteur 1.5
interaction 1.17
matrice de plan 2.7.1
méthode des moindres carrés 3.2
méthode graphique 3.1
mise en blocs 1.28
modéle 1.1
niveau 1.6
plan a deux niveaux 2.1.2
plan a surface de réponse 2.4
plan complétement emboîté 2.6.1
plan complétement randomisé 1.33
plan d'expérience 1.30
plan de «screening» 2.2
plan emboîté 2.6
plan embooté équilibré 2.6.1
plan en blocs 2.3
plan en blocs incomplete 2.3.4
plan en blocs incomplets équilibrés 2.3.4.1
plan en blocs incomplets partiellement équilibrés 2.3.4.2
plan en blocs randomisés 2.3.1
plan en blocs subdivisés 2.3.7
plan en carré gréco-latin 2.3.3
plan en carré latin 2.3.2
plan en parcelles subdivisées 2.3.6
plan factoriel 2.1
plan factoriel 2k 2.1.2.1
plan factorial complet 2.1
plan factoriel fractionné 2.1.1
plan factorial fractionné 2k -p 2.1.2.2
plan hiérarchisé 2.6
plan irrégulierement emboîté 2.6.2
plan optimal 2.7
plan optimal A 2.7.1.2
plan optimal D 2.7.1.1
plan optimal G 2.7.1.3
plan orthogonal 2.8
plan pour l'étude de mélanges 2.5
plan saturé 2.9
point central 1.36
point cubique 1.34
point étoile 1.35
randomisation 1.29
réplique 1.27
résidu 1.21
résolution de plan 2.1.3
rotativité 1.37
tracé d'interaction 3.1.2
tracé des effets principaux 3.1.1
tracé quantile des effets 3.1.3
trac é r é sidual 3.1.4
traitement 1.10
unit é exp é rimentale 1.9
variable de pr é diction 1.3
variable de r é ponse 1.2
zone du plan 1.4
ПРИЛОЖЕНИЕ А
(справочное)
Пояснения и примеры к терминам, приведенным в настоящих рекомендациях
К термину «Модель» ( 1.1)
Моде л ь состоит из трех частей. Первая часть - сам отклик ( 1.2) - объект моделирования. Вторая часть - детерминистическая или систематическая часть модели, включающая предсказывающие переменные ( 1.3). И последняя - третья часть - случайная или ошибка опыта, стохастическая часть модели, которая может быть достаточно хорошо известна. Например, член «ошибка» опыта может включать эффект рассеивания ( 1.14), который приводит к увеличению изменчивости в отклике с ростом фактических значений отклика.
Примеры
1 Время жизни некоторого компонента связано с условиями, в которых он находится.
2 Рассмотрим следующую модель:
yij = μ + αi + βj + εij ,
где yij - отклик на уровне i - го фактора А и на уровне j - го фактора В;
μ - общий средний отклик;
αi - увеличивающий эффект фактора А на уровне i ;
βj - увеличивающий эффект фактора В на уровн е j ;
εij - ошибка.
Часть, соответствующая отклику, состоит просто из yij . Часть, включающая предсказывающую переменную, состоит из μ + αi + βj - общего среднего отклика и двух величин, имеющих отношение к влиянию факторов. Случайная часть или ошибка этой модели состоит из εij , которая включает собственную изменчивость (вариабельность) процесса, порождающего отклик.
3 Широко используется следующая модель:
yijk = αi + βj + τij + εijk ,
где yijk - отклик k - го повторения;
αi - поправка, обусловленная фактором 1;
βj - поправка, обусловленная фактором 2 ;
τij - поправка , обусловленная взаимодействием факторов;
εijk - ошибка.
Термин «Поправка» используют здесь вместо термина «увеличивающий эффект» примера 2 , так как это формальная математическая модель, не включающая член, соответствующий общему среднему отклику. Более того, в этом примере вместо yij ( εij ) применяют обозначение yijk ( εijk ) , чтобы учесть возможность повторений.
4 Другая формальная модель имеет вид:
![]()
где yi - оклик, соответствующий xi ;
xj - предсказывающая переменна я;
![]() - средний отклик,
соответствующий xi ;
- средний отклик,
соответствующий xi ;
εi - ошибка.
Приведенное выше описание модели применимо не только к классической линейной модели с аддитивной ошибкой, но и к обобщенным линейным моделям, где ошибки можно описывать различными распределениями, включая биномиальное распределение, распределение Пуассона, показательное, гамма- и нормальное распределения.
К термину «Отклик» ( 1.2)
Отклик может быть вектором, если в каждом опыте регистрируют несколько откликов.
К термину «Предсказывающая переменная» ( 1.3)
То, насколько данная предсказывающая переменная управляема, определяет ее потенциальную роль в плане эксперимента. Предсказывающие переменные могут быть управляемыми (фиксированными), частично управляемыми (управляемыми лишь в течение короткого интервала времени или за счет больших расходов) или неуправляемыми (случайными).
Предсказывающая переменная может включать случайную составляющую, а может, например, быть из некоторого набора качественных классов, которые могут наблюдаться или назначаться без случайной ошибки.
К термину «Фактор» ( 1.5)
Фактор может служить некоторой особой причиной, влияющей на результат эксперимента. Фактор может быть связан с созданием блоков плана.
Термин «предсказывающая переменная» является синонимом термина «фактор», но в более широком смысле.
К термину «Уровень» ( 1.6)
Уровень фактора - это значение предсказывающей переменной или предиктора.
Термин «уровень (фактора )» обычно ассоциируется с количественной характеристикой. Тем не менее, его также применяют как термин, описывающий вариант или значение качественной характеристики.
Пример - Уровнями катализатора могут быть его наличие или отсутствие. Четыре уровня термообработки - это: 100 °С, 120 °С, 140 °С и 160 °С .
Отклики, наблюдаемые на различных уровнях фактора, содержат информацию для определения главного эффекта фактора в области его варьирования (в диапазоне, задаваемом уровнями) в данном эксперименте. Экстраполяция за эту область обычно бесполезна, если только нет серьезных оснований в предполагаемой модели зависимостей. Интер п оляция внутри области зависит от числа уровней и от их расположения. Интерполяция обычно имеет смысл, хотя и возможны нарушения непрерывности или многомодальные зависимости, обусловленные резкими переменами внутри области экспериментирования. Уровни могут ограничиваться некоторыми выбранными постоянными значениями (которые могут быть или не быть известными) или могут отбираться чисто случайно в заданном для исследования диапазоне. Метод анализа зависит от способа отбора уровней.
К термину «Ошибка опыта» ( 1.7)
Эксперименты, как правило, характеризуются тем, что при их повторении результаты варьируют от опыта к опыту, хотя экспериментальные материалы, окружающие условия и операции эксперимента тщательно контролируются. Таким образом, ошибка опыта - обычное явление. Эта вариация повышает степень неопределенности выводов на основе результатов, и, следовательно, ее надо учесть при получении выводов.
Конкретные уточнения этого широкого концептуального определения ошибки для индивидуальных откликов даются терминами «остаток» ( 1.21), «остаточная ошибка» ( 1.22) и «чистая ошибка» ( 1.23).
В связи с ошибкой опыта представляют интерес термины «повторяемость стандартного отклонения» и «воспроизводимость стандартного отклонения», которые непосредственно применимы в контексте планирования эксперимента, если план эксперимента построен в соответствии с условиями повторяемости и воспроизводимости соответственно ( ГОСТ Р 50779.10).
К термину «Компонента дисперсии» ( 1.8)
В модели yi = μ + τj + εij ,
где μ - общий средний отклик;
τi - случайно выбранный из бесконечного множества значений уровень;
τi и εij - случайные величины, распределения которых независимы. Как только для τi сделан выбор из бесконечного множества возможных уровней, анализ продолжается на основе реализации τi . В силу вероятностной структуры разумно рассмотреть уравнение дисперсий:
Var(yij ) = Var (τi) + Var(εij ),
где справа стоит στ 2 + σε 2 - сумма компонент дисперсии yij ;
Var - обозначение дисперсии случайных величин.
Можно также рассматривать модели, включающие иерархические (вложенные) или пересекающиеся факторы.
К терми н у «Блок» ( 1.11)
Термин «блок» произошел вследствие экспериментов, проводимых в сельском хозяйстве, в которых поле делилось на участки , обладающие одинаковыми условиями, например выветривание, близость подземных вод или толщина пахотного слоя. В других ситуациях блоки основаны на партиях исходных материалов, операторах, числе единиц, изученных за день, и так далее.
Обычно наличие блоков может влиять на то, какие обработки будут назначены экспериментальным единицам.
К терми н у «Одн офакто рный эксперимент» ( 1.12)
Пример - Рассмотрим модель
y = μi + ε ,
где y - отклик;
μi - средний отклик i - го уровня фактора;
ε - случайная величина, описывающая все другие эффекты и источники изменчивости.
Эта модель связывает отклик y с эффектом μi (в зависимости от соответствующего уровня фактора) и ошибкой ε . Различия в μi отражают влияние фактора на отклик (в данном случае среднее значение отклика как функция уровня фактора).
Альтернативное представление этой модели:
y = μ + αi + ε ,
где y - отклик;
μ - общий средний отклик;
αi - эффект увеличения, обусловленный i - м уровнем фактора;
ε - случайная величина, описывающая все другие источники изменчивости.
К термину «Главный эффект» ( 1.13)
Для фактора с двумя уровнями главный эффект относят к изменениям отклика при переходе с одного уровня на другой. Если уровни обозначены: минус 1 (меньшее значение) и плюс 1 (большее значение), то главный эффект оценивают как среднее отклика, когда уровень фактора равен плюс 1; минус среднее отклика, когда уровень фактора равен минус 1. Рассмотрим модель:
y = μ + βX + ε ,
где y , μ и ε - те же величины, что и в примере для о дн офакт орного эксперимента;
X равен либо минус 1, либо плюс 1 ;
β - поправка фактора X .
Отметим, что оценка β равна 1 / 2 главного эффекта фактора X . Если β = 0 , то X не влияет на среднее отклика (оно не зависит от того, какие значения принимает X : плюс 1 или минус 1 ), так что главный эффект X равен нулю.
К термину «Эффект рассеивания» ( 1.14)
Важно понимать, что фактор, слабо влияющий на среднее отклика, может сильно влиять на дисперсию отклика. В таких ситуациях некоторый уровень фактора может быть предпочтительнее, так как обеспечивает малую вариабельность или стабильность отклика. Возможно также, что фактор влияет и на среднее, и на дисперсию отклика.
К термину « Дву хфакто рный эксперимент» ( 1.15)
Если два фактора действуют, не влияя друг на друга, то применим термин «главный эффект». А именно: для каждого фактора главный эффект - его вклад в среднее отклика.
К термину «Взаимодействие» ( 1.17)
Взаимодействие указывает на непостоянство главного эффекта фактора в зависимости от уровней других факторов. Возможные варианты взаимодействия представлены на рисунке А.1.
Наиболее часто рассматривают взаимодействие двух факторов, которые более точно называют парным взаимодействием или взаимодействием первого порядка. Возможно, что три фактора, например А, В и С, взаимодействуют так, что взаимодействие первого порядка А и В зависит от уровня фактора С. В этом случае есть взаимодействие второго порядка. Аналогично, можно рассмотреть взаимодействия третьего, четвертого и т.д. порядков.
На рисунке А.1 графически представлены варианты взаимодействия факторов для третьего примера к термину «модель» ( 1.1), в котором приведена формальная модель эксперимента с двумя факторами и д ву хф акторны м взаимодействием или взаимодействием первого порядка τij между ними.
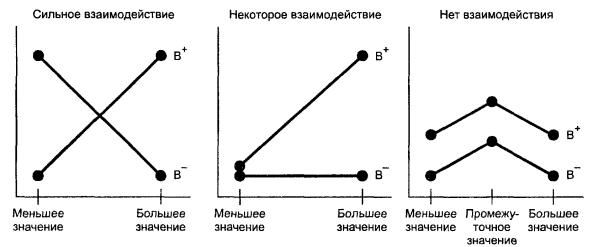
Обозначения:
В+ - большее значение уровня факторов;
В - - меньшее значение уровня факторов.
Рисунок А. 1 - Варианты взаимодействия
К термину «Смешивание» ( 1.18)
Смешивание - важный прием, позволяющий эффективно применять разбиение на блоки в некоторых планах экспериментов. Это достигают намеренным отнесением некоторых эффектов (главных) или взаимодействий к малосущественным и смешиванием их в планах с эффектами блоков так, чтобы сделать другие более важные факторы свободными от таких сложностей. Смешивание можно намеренно использовать для уменьшения числа опытов в плане эксперимента ( 1.30). Иногда смешивания возникают из-за изменений плана в процессе проведения эксперимента или из-за неполного планирования, что может уменьшить значимость эксперимента или совсем его обесценить.
К термину «Нелинейность» ( 1.20)
Понятие нелинейности имеет смысл в случае с количественной, а не качественной предсказывающей переменной. Обнаружение нелинейности требует, чтобы фактор мог варьировать более чем на двух уровнях. В некоторых случаях повторение центральной точки (фактор принимает значение посередине между минимальным и максимальным значениями) может обнаружить и оценить нелинейность. Увеличение числа уровней фактора может понадобиться для наблюдения нелинейности.
Возвращаясь к модели из примера для о дн офак торного эксперимента ( 1.12), нелинейность можно смоделировать в следующей форме:
Y = μ + β Х + γ Х 2 + ε ,
где γ - поправка фактора X 2 .
Если коэффициент у отличается от 0 , это свидетельствует о нелинейности по сравнению с простой линейной зависимостью.
К термину «Остаток» ( 1.21)
Предсказанное значение отклика определяют исходя из постулируемой модели, параметры которой оцениваются по имеющимся данным.
Примеры
1 ![]() - остаток,
соответствующий экспериментальной единице с фактором А, установленным на уровне
i , и фактором В, установленным на уровне j в соответствии с моделью примера 2 для термина
«модель» ( 1.1) .
- остаток,
соответствующий экспериментальной единице с фактором А, установленным на уровне
i , и фактором В, установленным на уровне j в соответствии с моделью примера 2 для термина
«модель» ( 1.1) .
2 ![]() - остаток в модели
примера 3 для термина «модель» ( 1.1).
- остаток в модели
примера 3 для термина «модель» ( 1.1).
3 ![]() - остаток в модели примера 4 для термина «модель» ( 1.1).
- остаток в модели примера 4 для термина «модель» ( 1.1).
К термину «Остаточная ошибка» ( 1.22)
Под предсказанным значением отклика понимают оценку отклика для данной обработк и, определенную по эмпирической модели, полученной по экспериментальным данным в соответствии с постулированной моделью.
Пример
- Если ![]() и
и ![]() - оценки μ и β [см. пояснение к термину «главный
эффект» ( 1.13 )],
то
- оценки μ и β [см. пояснение к термину «главный
эффект» ( 1.13 )],
то ![]() - остаточная ошибка
данного наблюденного значения y при данном значении предсказывающей переменной x .
- остаточная ошибка
данного наблюденного значения y при данном значении предсказывающей переменной x .
Остаточная ошибка включает экспериментальную ошибку и определенные источники вариации, не учитываемые данной моделью.
Дисперсию остаточной ошибки обычно оценивают в эксперименте путем вычитания объединенной суммы квадратов членов, включенных в постулированную модель, из общей суммы квадратов и делением полученной разности на соответствующую разность «степеней свободы» (см. пример 1 для термина «регрессионный анализ» и пример для термина « дисперсионный анализ»).
К термину «Чистая ошибка» ( 1.23)
Если повторения были проведены только для центральной точки плана, то выборочная дисперсия откликов в ней дает оценку дисперсии чистой ошибки. Если повторения были получены при различных обработках, то общую оценку дисперсии чистой ошибки можно получить объединением оценок для различных обработок.
Пример - Возвращаясь к примеру 3 для термина «модель», находим, что оценка дисперсии чистой ошибки для фиксированной пары ( i , j ) равна:
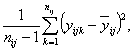
где
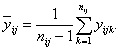
Если повторения проводились при разных обработках [при каждой паре ( i , j )], то объединенная оценка дисперсии чистой ошибки будет иметь вид:
![]()
где i = 1 , …, I ; j = 1 , …, J ; k = 1 , …, nij;
N - общее число уровней.
Термин «чистая ошибка» на практике используют в двух разных ситуациях. Иногда чистую ошибку относят к дисперсии генеральной совокупности ( σ 2 ) в связи с математической моделью. В других ситуациях чистую ошибку относят к «выборочной» или «эмпирической» чистой ошибке, которая вместе с оценкой остаточной ошибки обеспечивает основу для проверки адекватности модели. Из примеров, иллюстрирующих термин «модель », только пример 3 с повторениями позволит непосредственно провести оценку чистой ошибки. С математической точки зрения чистую ошибку можно рассматривать как Var ( εij ) в примере 2 , Var ( εijk ) - в примере 3, Var ( εi ) - в примере 4 .
К термину «Контраст» ( 1.24)
Для наблюдений у 1 , …, у n линейная функция a 1 y 1 + a 2 y 2 +, …, + anyn служит контрастом тогда и только тогда, когда a 1 + a 2 +, …, + an = 0 и не все ai равны нулю ( i = 1 , …, n ).
Примеры
1 Некоторый фактор варьировался на трех уровнях, а полученные результаты равны y 1 , y 2 и y 3 . Среди множества вопросов, которые можно обратить к полученным данным, рассмотрим следующие:
вопрос 1 - какова разность между откликом для первого и третьего уровней (временно игнорируем средний уровень)? Подходящий контраст для ответа на вопрос 1 требует значений y 1 и y 3 ;
вопрос 2 - если уровни равноудалены один от другого, то нет ли свидетельства того, что структура откликов указывает на квадратичную, а не на линейную зависимость? Здесь среднее из y 1 и y 3 можно сравнить с y 2 . (Если зависимость линейная, то y 2 должен лежать близко к линии, соединяющей y 1 и y 3 , то есть быть приблизительно равным их среднему).
Отклик y 1 y 2 y 3
Коэффициенты контраста для вопроса 1 -1 0 +1
Контраст 1 - y 1 + y 3
Коэффициенты контраста для вопроса 2 -1/2 +1 -1/2
Контраст 2 - y 1 /2 + y 2 - y 3 /2
Этот пример иллюстрирует регрессионный тип исследования непрерывных переменных величин. Часто удобнее использовать для коэффициентов контраста целые числа вместо дробей. В этом случае коэффициенты для контраста 2 будут (-1 , +2 , -1 ).
2 Пример с дискретными уровнями фактора может породить другую пару вопросов.
Предположим, что существуют три источника сырья, один из которых A 1 - использует новую технологию производства , а А2 и A 3 - применяют обычные методы. Вопрос 1 - отличается ли поставщик A 1 , использующий новую технологию, от А 2 и А 3 , работающих по старинке? Здесь y 1 сравнивают со средним из y 2 и y 3 (контраст 1 ). Вопрос 2 - различаются ли те два поставщика, которые используют старую технологию? Здесь сравнивают y 2 и y 3 (контраст 2 ). Структура коэффициентов контрастов аналогична предыдущему примеру, хотя интерпретация результатов иная.
Отклик y 1 y 2 y 3
Коэффициенты контраста для вопроса 1 -2 +1 +1
Контраст 1 -2 y 1 + y 2 + y 3
Коэффициенты контраста для вопроса 2 0 -1 +1
Контраст 2 - y 2 + y 3
К термину «Ортогональный контраст» ( 1.26)
Примеры
1 Пример неортогонального контраста
y 1 y 2 y 3
ai 1 Контраст 1 -1 0 +1
ai 2 Контраст 2 0 -1 +1
ai 1 ai 2 0 0 +1
Σai 1 ai 2 = 1 , где ai 1 ai 2 - коэффициенты контраста, то есть набор контрастов неортогонален.
2 Пример ортогонального контраста
y 1 y 2 y 3
ai 1 Контраст 1 -1 0 +1
ai 2 Контраст 2 -1 +2 -1
ai 1 ai 2 +1 0 -1
Σai 1 ai 2 = 0 , где ai 1 ai 2 - коэффициенты контраста, то есть набор контрастов ортогонален.
К термину «Ортогональное расположение» ( 1.26)
В связи с планом отсеивания (термин п. 2.2) возникает связанная с понятием «ортогональное расположение» концепция эффективности. Отметим, что план отсеивания - это одно из возможных применений ортогональных расположений. План эффективности d - это полный факторный план с любым числом факторов. Эффективность, равная единице, означает, что уровни каждого фактора появляются одинаковое число раз (это иногда называют сбалансированным фактором). Ортогонал ь ное расположение имеет эффективность, равную двум. Объем подмножества d известен как эффективность.
К термину «Повторение» ( 1.27)
Ограничения при проведении эксперимента могут потребовать , чтобы повторения проводились последовательно, а не случайно. Неформально подобная ситуация соответствует повторению, но общего согласия по поводу этого термина не существует. В настоящих рекомендациях термин «повторение» означает получение большого количества откликов для фиксированного набора уровней предсказывающих переменных.
К термину «Разбиение на блоки» ( 1.28)
Блоки обычно выбирают, чтобы учесть эффекты неслучайных причин в дополнение к тем, что введены для изучения как основные факторы, которые может быть сложно или даже невозможно поддерживать постоянными для всех экспериментальных единиц в полном эксперименте. Эффекты этих неслучайных причин можно минимизировать внутри этих блоков, что позволяет получить более однородное экспериментальное подпространство. При анализе экспериментальных результатов надо принимать во внимание эффект разбиения эксперимента на блоки.
Те блоки, которые включают полный набор обработок, называют полными блоками. Те, которые образуют только часть полного набора, называют неполными блоками. Когда обработки применяют к парам, эти пары становятся блоками.
К термину «Рандомизация» ( 1.29)
Рандомизация пытается защитить от смещений, обусловленных причинами, которые не были непосредственно учтены в эксперименте. Рандомизация может заметно снизить потенциально временные или пространственные эффекты.
К термину «Спланированный эксперимент» ( 1.31)
Цель планирования эксперимента состоит в том, чтобы обеспечить наиболее экономичный и эффективный метод достижения правильных и относящихся к делу выводов от эксперимента. Выбор соответствующего плана эксперимента зависит от рассматриваемых вопросов, таких как степень общности выводов, значимость эффектов, для которых требуются высокая вероятность обнаружения, однородность экспериментальных единиц и стоимость проведения эксперимента. Правильно спланированный эксперимент часто позволяет относительно легко проводить статистический анализ и интерпретировать его результаты.
К термину «Эволю ц ионное планирование» ( 1.32)
Главная цель эволюционного планирования - получение знаний для совершенствования процесса вместе с продукцией путем использования планируемых экспериментов с относительно малыми сдвигами в уровнях факторов (в пределах производственных допусков) при минимальных затратах. Диапазон варьирования факторов в любом отдельном эксперименте ЭВОП обычно весьма мал, чтобы избежать производства продукции за пределами поля допуска, и это может потребовать известного числа повторений для снижения эффекта случайной вариации.
К термину «Полностью ра н домизированный план» ( 1.33)
Полностью рандомизированный план применим только лишь в предположени и, что все экспериментальные единицы достаточно однородны (то есть отсутствуют систематические отличия) или же нет информации о возможной неоднородности.
К термину «Точка в вершине куба» ( 1.34)
Эти точки как раз тот тип точек , которые наблюдают в полном двухуровневом или дробном факторном плане ( 2.1). Всего 2 k точек в вершине куба можно использовать в центральном композиционном плане (см. пример 1 для термина «план поверхности отклика»).
К термину «Звездная точка» ( 1.35)
Все звездные точки имеют единственн ую ненулевую компоненту, равную (+ α ) или (- α ). В центральных композиционных планах обычно используют 2 k звездных точек.
К термину «Центральная точка» ( 1.36)
Все компоненты центральной точки равны нулю, так что вектор имеет вид ( 0 , 0 , …, 0 ), и соответствуют центру плана в кодированных переменных. Число этих точек, например n 0 , выбирают таким образом , чтобы достичь различных целей в планах поверхностей отклика. Центральные точки иногда повторяют для получения оценки чистой ошибки исследуемого процесса.
К термину «Полный факторный эксперимент» ( 2.1)
Из факторного эксперимента можно получить все взаимодействия и главные эффекты.
Факторный эксперимент в символьной записи обычно описывают как произведение числа уровней всех факторов. Например эксперимент, основанный на трех уровнях фактора А, двух уровнях фактора В и четырех уровнях фактора С, будет обозначен как 3 ×2×4 -факт орны й план. Произведение этих чисел дает число обработок.
Если факторный эксперимент включает факторы, варьируемые на одинаковом числе уровней, то описание обычно дают в форме числа уровней в степени числа факторов k . Так, эксперимент с двумя факторами на трех уровнях каждый будет обозначен как 32 -факт орны й эксперимент ( k = 2 ) и требует 9 экспериментальных единиц для всех данных обработок.
Полные факторные планы иногда называют также перекрестными планами.
К термину «Дроб н ый факторный эксперимент» ( 2.1.1)
Обычно дробный факторный эксперимент - это простая доля от всего множества возможных обработок. Например , половина, четверть и т.п.
К термину «Факторный эксперимент 2 k » ( 2.1.2.1)
Пример - Можно провести факторный эксперимент 24 для исследования влияния на процесс четырех факторов: давления, температуры, катализатора и оператора.
Пусть А - давление (высокое или низкое), В - температура (высокая или низкая ), С - катализатор (есть или нет), D - соответствует оператору (первый или второй).
Факторный эксперимент 24 состоит из 16 обработок, как указано в таблице А.1. Символы «-» и «+» означают два возможных уровня фактора. Как правило, «-» означает низкий уровень, а « +» - высокий, хотя выбор обозначений уровней произволен.
Порядок, указанный в таблице А.1 , известен как стандартный порядок Йейтса и может пригодиться на стадии анализа. Реальный порядок, в котором выполняют указанные обработки, надо определить с помощью рандомизации ( 1.29), Первый фактор А имеет чередующие знаки (-, +, -, + и т.д.). Второй фактор В имеет два минуса, два плюса. Третий фактор С имеет четыре минуса, четыре плюса. И последни й фактор D имеет 8 минусов и 8 плюсов. Далее в настоящих рекомендациях минус будет обозначаться как -1 , а плюс - как +1 .
Вторая графа таблицы содержит краткое обозначение обработок. Наличие прописной буквы соответствует высшему уровню фактора, а отсутствие - низшему. Случай, когда все факторы находятся на низшем уровне, обозначают « (1 )» .
Таблица А. 1 - Пример факторного эксперимента 24
|
Экспериментальная единица |
Обработка |
План |
|||
|
|
|
A |
В |
C |
D |
|
1 |
( 1 ) |
- |
- |
- |
- |
|
2 |
а |
+ |
- |
- |
- |
|
3 |
b |
- |
+ |
- |
- |
|
4 |
а b |
+ |
+ |
- |
- |
|
5 |
с |
- |
- |
+ |
- |
|
6 |
ас |
+ |
- |
+ |
- |
|
7 |
b с |
- |
+ |
+ |
- |
|
8 |
abc |
+ |
+ |
+ |
- |
|
9 |
d |
- |
- |
- |
+ |
|
10 |
ad |
+ |
- |
- |
+ |
|
11 |
bd |
- |
+ |
- |
+ |
|
12 |
abd |
- |
+ |
- |
+ |
|
13 |
cd |
- |
- |
+ |
+ |
|
14 |
acd |
+ |
- |
+ |
+ |
|
15 |
bcd |
- |
+ |
+ |
+ |
|
16 |
abcd |
+ |
+ |
+ |
+ |
Полный факторный эксперимент позволяет произвести оценку всех главных эффектов и взаимодействий. В приведенном примере есть 4 главных эффекта (А, В, С, D ), шесть взаимодействий первого порядка (АВ, АС, AD , BC , BD , CD ), четыре взаимодействия второго порядка ( ABC , ABD , ACD , BCD ) и одно взаимодействие третьего порядка ( ABCD ).
Каждый из эффектов (например эффект А, взаимодействие между А и В и даже взаимодействие третьего порядка между А, В, С и D ) можно оценить с помощью коэффициентов контрастов (см. пояснение к термину «регрессионный анализ »).
К термину «Дробный факторный эксперимент 2( k - p ) » ( 2.1.2.2)
Для большого числа факторов полный факторный эксперимент 2 k может потребовать большего числа обработок, чем это физически возможно. При тщательном отборе факторов дробный факторный эксперимент может дать почти столько же информации, как и полный факторный эксперимент. В частности, выбор производят таким образом, чтобы эффекты и взаимодействия, представляющие практический интерес, смешивались лишь с теми эффектами, которыми можно пренебречь.
Для p = 2 получаемый эксперимент будет полурепликой, при p = 4 - чет вертьрепл икой и т.д.
Дробный факторный эксперимент 3 2( k - p ) получают путем разделения факторов на две группы: главную, содержащую k - p факторов, и вторичную, содержащую p факторов. Для k - p факторов главной группы строят полный факторный эксперимент с 2( k - p ) экспериментальными единицами. Уровни каждого из факторов вторичной группы определяют в терминах уровней факторов главной группы. Множество из p уравнений, которые определяют факторы вторичной группы в терминах факторов главной группы, называют генерирующим соотношением, так как они генерируют план. Множество из p уравнений генерирующего соотношения можно использовать для вычисления 2( k - p ) - 1 уравнений определяющего соотношения (контраста), которое задает свойства плана.
Пример - Рассмотрим эксперимент с 6 факторами и 16 обработками. При этом можно провести дробный факторный эксперимент 26-2 ( k = 6 ; p = 2 ). 4 фактора (А, В, С, D ) можно выбрать как основу для полного факторного эксперимента. Два других фактора (Е и F ) можно выразить через А, В, С, D . Один из возможных вариантов: Е = ABC и F = BCD . (Отметим, что 4 буквенные последовательности или строки символов ABDE и BCDF , получаемые в этой конструкции, известны как слова. Например, ABC - трехбуквенное слово, ABCEG - п ятибук венное и т.д.). Используя для обозначений уровней факторов +1 и -1, уровни А, В, С определяют уровень фактора Е через их произведение, а уровни В, С, D - уровень фактора F через произведение BCD . Например, для экспериментальной единицы номер 1 уровни А, В, С, D даны в таблице А.1 Уровни Е и F для экспериментальной единицы номер 1 тоже находятся на нижних уровнях. Главный эффект Е - это совместный эффект со взаимодействием второго порядка ABC , а главный эффект F - совместный с BCD . Полный совместный эффект I (смешивающая структура) может быть найден из генерирующего соотношения I = АВСЕ = BCDF = ADEF .
К термину «Разрешающая способность плана» ( 2.1.3)
Разрешающая способность плана описывает степень смешивания в конкретном плане. Число, описывающее длину, обычно обозначают римскими цифрами. Наиболее часто встречающиеся на практике ситуации с разрешающей способностью - III , IV , V .
Для плана с разрешающей способностью III кратчайшая строка (кроме I ) имеет длину 3 символа и для этого плана главные эффекты не смешиваются с другими главными эффектами. По крайней мере один главный эффект смешивается с д ву хфакторны м.
Для плана с разрешающей способностью IV главные эффекты не смешиваются с другими главными эффектами, а также с д ву хфакт орны ми взаимодействиями.
Для плана с разрешающей способностью V главные эффекты и дв у хфакт орны е взаимодействия не смешиваются с другими главными эффектами и двухфакторными взаимодействиями.
Чем выше разрешающая способность, тем большее число эффектов (главных или взаимодействий) можно определить недвусмысленно. Если есть два плана с равным числом факторов и экспериментальных единиц, то надо выбирать тот, разрешающая способность которого выше.
Пример - Продолжим рассмотрение примера к термину «дробный факторный эксперимент» ( 2.1.2.2). Разрешающую способность плана для этого дробного факторного плана 26-2 ( k = 6 , р = 2 ) получим из его определяющего соотношения. Точнее, разрешающая способность плана - это длина самого короткого (кроме I ) слова в определяющем соотношении. При условии, что IA = AI = A ; IB = BI = В; I = А 2 = В 2 = = С 2 и так далее, генерирующее соотношение Е = ABC эквивалентно ЕЕ = АВСЕ, что в свою очередь эквивалентно I = АВСЕ. Аналогично F = BCD приводит к I = BCDF . Определяющее соотношение выводят из обобщенного взаимодействия АВСЕ × BCDF = ADEF . Самое короткое слово имеет длину 4 символа, а значит, разрешающая способность равна IV . Генераторы планов обычно называют генераторами Бокса-Хантера.
К термину «План отсеивания» ( 2.2)
Такие эксперименты обычно сосредоточены на исследовании главных эффектов, а наличие взаимодействий ведет к осложнениям при анализе и, как результат, к дополнительным экспериментам для разрешения неопределенности.
Примеры
1 Дробные факторные планы 2 k - p (особенно с высокой степенью дробности) могут рассматриваться как планы отсеивания.
2 Пл акк етт и Берман предложили набор таких двухуровневых планов с числом обработок, кратным 4 . Их планы обычно используют в тех ситуациях, когда число исследуемых главных эффектов приблизительно равно числу различных допустимых обработок. Например, 12 обработок плана Плаккетта-Б ерман а, приведенного в таблице А.2, можно использовать для выявления 11 главных эффектов. В этом плане наличие д ву хфакт орного взаимодействия (например АВ ) может повлиять на оценку главных эффектов С, D , … , К.
Таблица А. 2 - План эксперимента с числом обработок, кратным 4
|
Номер опыта |
Уровни факторов для главных эффектов |
||||||||||
|
А |
В |
С |
D |
Е |
F |
G |
Н |
I |
J |
K |
|
|
1 |
+ |
- |
+ |
- |
- |
- |
+ |
+ |
+ |
- |
+ |
|
2 |
+ |
+ |
- |
+ |
- |
- |
- |
+ |
+ |
+ |
- |
|
3 |
- |
+ |
+ |
- |
+ |
- |
- |
- |
+ |
+ |
+ |
|
4 |
+ |
- |
+ |
+ |
- |
+ |
- |
- |
- |
+ |
+ |
|
5 |
+ |
+ |
- |
+ |
- |
- |
+ |
- |
- |
- |
+ |
|
6 |
+ |
+ |
+ |
- |
+ |
+ |
- |
+ |
- |
- |
- |
|
7 |
- |
+ |
+ |
+ |
- |
+ |
+ |
- |
+ |
- |
- |
|
8 |
- |
- |
+ |
+ |
+ |
- |
+ |
+ |
- |
+ |
- |
|
9 |
- |
- |
- |
+ |
+ |
+ |
- |
+ |
+ |
- |
+ |
|
10 |
+ |
- |
- |
- |
+ |
+ |
+ |
- |
+ |
+ |
- |
|
11 |
- |
+ |
- |
- |
- |
+ |
+ |
+ |
- |
+ |
+ |
|
12 |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
- |
Многие планы Плаккетта -Б ермана связаны с матрицами Ад амара, которые первоначально были выведены теоретически, но позже оказались полезными в планировании эксперимента. Матрицы Адамара легко сконструировать, если известен один столбец (или строка) матрицы. Как возможный вариант предположим, что нижняя строка состоит из одних минусов. Остальные столбцы получают из первого столбца сдвигом его на одну позицию вправо вниз, при этом его элемент с номером 11 переходит в первую позицию. Эту процедуру повторяют до тех пор, пока не заполнится вся матрица. Примеры некоторых из этих матриц приведены ниже. Для каждого случая достаточно указать положение знака плюс в первом столбце (таблица А.3).
Таблица А .3 - Номер обработки, содержащей знак плюс в первом столбце условной таблицы уровней факторов
|
Число обработок п |
Номер опыта |
|
12 |
1 , 2 , 4 , 5 , 6 , 10 |
|
20 |
1 , 2 , 5 , 6 , 7 , 8 , 10 , 12 , 17 , 18 |
|
24 |
1 , 2 , 3 , 4 , 5 , 7 , 9 , 10 , 13 , 14 , 17 , 19 |
Отметим, что строки, указанные выше для п = 12 , согласованы с планом, описанным в примере 2 . Многие из планов Плаккетта-Б ермана можно построить, применяя этот общий подход с использованием элементов одного столбца как основы. В случаях, когда п = 28 , 52 , 76 , 92 и 100 , этот простой подход не работает.
Та гути популяризовал использование планов Плаккетта-Б ермана и ввел некоторые аббревиатуры: план L 12 эквивалентен плану Плаккетта-Б ермана с 12 обработками, приведенными выше. L 20 - это план Пл акк ет та-Берман а с 20 обработками. Следует отметить, что « L - пл ан» обычно описывает значение матрицы плана в другом порядке, чем в матрицах Адамара.
Планы Плаккетта -Б ермана можно адаптировать для использования в сверхнасыщенных планах, когда число факторов больше числа обработок.
К терми н у «Блочный план» ( 2.3)
Неоднородность экспериментальных единиц, в том случае если ее не учитывают в плане эксперимента, может уменьшить количество информации, получаемой из эксперимента из-за роста наблюдаемой вариации. Учет этого факта в плане может увеличить возможность эксперимента в достижении поставленной цели.
К термину «Рандомизированный блочный план» ( 2.3.1)
Рандомизированные блочные планы - это те, в которых экспериментальные единицы сгруппированы в блоки, причем единицы в одном блоке более однородны, чем единицы в разных блоках. В каждом блоке экспериментальным единицам назначают обработки случайным образом. Относительные эффекты обработок можно оценить без влияния эффектов других блоков.
К термину «План «латинский квадрат» ( 2.3.2)
План «латинский квадрат» включает три фактора: главный фактор, ассоциированный с обработкой, и два вторичных фактора, ассоциированных с эффектами блоков; все факторы имеют равное число уровней. Всего существует h 2 ( h ≥ 2 ) экспериментальных единиц, классифицированных в соответствии с двумя блоковыми факторами (фактор столбцов и фактор строк). Существуют h уровней главного фактора, которые распределены по h 2 экспериментальным единицам таким образом, что каждая строка и каждый столбец содержат каждый уровень обработки ровно один раз. Таким образом, план «латинский квадрат» - это обобщение рандомизированного блочного плана на случай двух блоковых факторов или источников внешней вариации. Ограничением служит то, что число уровней главного фактора и блоковых факторов должно быть одинаковым.
Пример - Ниже приведены три латинских квадрата 4 × 4 , каждый из которых может быть основой плана «латинский квадрат». 4 строки соответствуют уровням одного блочного фактора, а 4 столбца - другого. 4 уровня обработки обозначены буквами А, В, С и D .
ABCD ABCD ABCD
BADC DCBA CDAB
CDAB BADC DCBA
DCBA CDAB BADC
План «латинский квадрат» обычно используют для исключения влияния двух выраженных блоковых эффектов, не представляющих значительного интереса, путем взаимной нейтрализации их действия. Блоки связывают со строками и столбцами квадрата: например, строки могут означать дни, а столбцы - операторов. Число уровней главного фактора и каждого из блочных факторов должно быть одинаковым. Рандомизацию можно провести, назначая случайно уровни главного фактора буквам, случайно выбирая латинский квадрат из списка или с помощью специальных процедур и назначением уровней блочных факторов случайным строкам и столбцам квадрата. [Всего есть 1 (2 × 2 ); 12 (3 × 3 ); 576 (4 × 4 ); 161280 (5 × 5 ) латинских квадратов. Из них 1 (2 × 2 ); 1 (3 × 3 ); 4 (4 × 4 ); 56 (5 × 5 ) «стандартных» латинских квадратов, в которых первая строка и первый столбец записаны в алфавитном порядке и из которых остальные квадраты можно получить перестановками строк и столбцов].
Основное предположение состоит в том, что эти блочные факторы не взаимодействуют (не вызывают побочных эффектов) с главным изучаемым фактором или друг с другом. Если это предположение неверно, то мера остаточной ошибки возрастает и эффект фактора смешивается с такими взаимодействиями. Когда предположения верны, план полезен для минимизации числа экспериментов. Иногда другие главные факторы используют в качестве блочных факторов, так что может быть три главных фактора вообще без блочных факторов. Это эквивалентно дробному факторному эксперименту в предположении отсутствия взаимодействий. Некоторые планы дробных факторных экспериментов образуют латинские квадраты, и, может быть, лучше подходить к этой проблеме с точки зрения дробного факторного эксперимента для более полного понимания предположений, сделанных относительно взаимодействий.
К термину «План г реко-л атинский квадрат» ( 2.3.3)
План «греко-латинский квадрат» включает 4 фактора и всего существует h 2 ( h ≥ 3 ) экспериментальных единиц, классифицированных по трем блочным факторам (например, строчный фактор, столбцовый фактор и греческая буква), каждый из которых имеет h уровней. Имеем h уровней главного фактора, которые назначены h экспериментальным единицам случайным образом так, что каждая обработка появляется в каждой строке и столбце только один раз и с греческой буквой тоже только один раз.
Говорят, что два латинских квадрата ортогональны, если каждая буква в одном квадрате совпадает точно один раз с каждой буквой в другом квадрате. Пары ортогональных латинских квадратов можно скомбинировать для получения греко-латинских квадратов.
Греко-латинские квадраты позволяют объединять три блоковые переменные, каждая из которых имеет то же число уровней, что и главный фактор.
Пример - Греко-латинский квадрат 4 × 4 представлен ниже.
А α В β Cγ Dδ
Bδ Aγ Dβ Cα
С β Dα Aδ Bγ
Dγ Cδ В α А β
Фактор 1 задан строками, фактор 2 задан столбцами, а фактор 3 представлен греческими буквами. Главный фактор (4 ) представлен латинскими буквами.
К термину «Непо лн облочны й план » ( 2.3.4)
Рандомизированный блочный план ( 2.3.1) можно рассматриват ь как «полный» блочный план отдельного блока неполноблочного плана, подчеркивающий, что каждый блок имеет достаточное число экспериментальных единиц для данного числа обработок.
К термину «Сбалансированный непол но блочный план» ( 2.3.4.1)
Термин «сбалансированный» относят к постоянному числу пар, «неполный» - к невозможности исследовать каждый уровень каждого фактора в каждом блоке и термин «блок» относится к стратегии проведения эксперимента на однородных множествах экспериментальных единиц.
Примеры
1 Рассмотрим ситуацию с 4 обработками и 6 блоками, 2 обработками на блок ( l = 4 , k = 2 , b = 6 , λ = 1 ). Предположим более точно, что надо изучить 4 уровня ( T 1 , Т 2 , Т 3 , Т 4 ) главного фактора, но только 2 уровня можно рассмотреть в один день . Если для выполнения эксперимента отведено 6 дней, то применим следующий план, представленный в таблице А.4.
Таблица А. 4 - Сбалансированный неполноблочный план
|
День |
План эксперимента для уровней |
|||
|
Т1 |
Т2 |
Т3 |
Т4 |
|
|
1 |
* |
* |
|
|
|
2 |
|
|
* |
* |
|
3 |
* |
|
* |
|
|
4 |
|
* |
|
* |
|
5 |
* |
|
|
* |
|
6 |
|
* |
* |
|
В этом примере все возможные пары обработок (отмечены звездочками) появляются только один раз в каждом блоке.
2 Рассмотрим ситуацию с 6 уровнями главного фактора, с 10 блоками и с 3 уровнями на блок ( l = 6 , k = 3 , b = 10 , λ = 2 ). В этом случае можно предположить, что нужны 20 блоков, так как для 6 уровней существуют 20 возможных троек. Рассмотрим следующий набор обработок, где каждый блок задан тройкой:
( T 1 , Т 2 , Т3 ), (Т1, Т2, Т4 ), (Т1, Т3 , Т5 ), (Т1, Т4 , Т6 ), (Т1, Т5 , Т6 ),
(Т 2 , Т3 , Тб ), (Т2 , Т4, Т5 ), (Т2 , Т5, Т6 ), (Т3 , Т4 , Т5 ), (Т3 , Т4 , Т6 ).
Здесь каждая пара уровней появляется в каждом блоке ровно 2 раза, показывая, что 10 блоков может быть достаточно.
3 Рассмотрим ситуацию с 7 уровнями и 7 блоками с 4 уровнями на блок ( l = 7 , k = 4 , b = 7 , λ = 2 ) (таблица А.5).
Таблица А. 5 - Данные примера 3
|
Блок |
Уровни главного фактора |
|||
|
1 |
1 |
2 |
3 |
6 |
|
2 |
2 |
3 |
4 |
7 |
|
3 |
3 |
4 |
5 |
1 |
|
4 |
4 |
5 |
6 |
2 |
|
5 |
5 |
6 |
7 |
3 |
|
6 |
6 |
7 |
1 |
4 |
|
7 |
7 |
1 |
2 |
5 |
Сбалансированный неполноблоч ны й план подразумевает, что каждый уровень главного фактора появляется одинаковое число раз ( h ) в эксперименте и что имеют место следующие отношения:
bk = lh , b ≥ l и h ( k - 1 ) = λ ( l - 1 ).
Так как каждая буква в этих уравнениях представляет целое число, то ясно, что только ограниченный набор комбинаций ( l , k , b , h , λ ) подходит для конструирования сбалансированного неполноблочного плана. Однако наличие пятерки чисел ( l , k , b , h , λ ) не означает, что такой план существует.
Для рандомизации следует расположить блоки и уровни внутри каждого блока независимым случайным образом.
К термину «Частично сбалансированный неполноблочный план» ( 2.3.4.2)
Неполноблочный план с l уровнями и b блоками - это частично сбалансированный неполноблочный план с m ≥ 2 ассоциированными классами, если выполнены следующие условия:
а) каждый блок содержит k < l различных уровней;
б) каждый уровень появляется в h блоках;
в) между уровнями существует отношение, удовлетворяющее:
- любые два уровня: либо 1, либо 2 ,..., либо m ассоциированы, это отношение симметрично (если уровень αi ассоциирован с уровнем β , то βi ассоциирован с уровнем α );
- каждый уровень имеет ni i -а ссоциированных уровней, где i = 1, 2, … , m ; причем значения ni не зависят от выбранного уровня;
- для данной пары α и βi -ассоциированных элементов число уровней, которые j -ассоциирова ны с α и k , ассоциированными с β , равно pijk где i , j , k = 1 , …, m . Число pijk не зависит от пары ( α , β ) i - ассоциированных уровней;
г) любые два уровня, которые i - ассоциированы, появляются одновременно в λi блоках, причем все λi равны ( i = 1 , 2 , …, m ).
Целые числа l , b , h , k , λ 1 , λ 2 , …, λm ; n 1 , n 2 , … , nm ; pijk , где i , j , k = 1 , 2 , …, m связаны следующими соотношениями:
l·h = b·k ;
n 1 λ1 + n2λ2 +, …, + nmλm = h (k - 1 );
n 1 + n 2 +, …, + nm = l - 1 ;
nipijk = njpjik = nkpkij .
Пример - Рассмотрим ситуацию, когда l = 6 , k = 4 , b = 6 , h = 4 , ni = 1, n 2 = 4 , λ 1 = 4 , λ 2 = 2 , как это описано в таблице А.6.
Таблица А. 6 - Данные примера для частично сбалансированного неполноблочного плана
|
Блок |
Уровни главного фактора |
|||
|
1 |
1 |
4 |
2 |
5 |
|
2 |
2 |
5 |
3 |
6 |
|
3 |
3 |
6 |
1 |
4 |
|
4 |
4 |
1 |
5 |
2 |
|
5 |
5 |
2 |
6 |
3 |
|
6 |
6 |
3 |
4 |
1 |
В этом плане каждый уровень появляется четыре раза ( h = 4 ), начиная с любого уровня, например с первого уровня (п1 = 1 ). Например, уровень 4 появляется с уровнем 1 в четырех блоках ( λ 1 = 4 ) и на четырех уровнях ( n 2 = 4 ). Уровни 2 , 3 , 5 , 6 с уровнем 1 появляются в двух блоках ( λ 2 = 2 ). Параметры n 1 , n 2 , λ 1 , λ 2 одни и те же, независимо от начального уровня.
К термину «Квадрат Юдена» ( 2.3.5)
Квадрат Юдена можно рассматривать как план с двумя блоковыми факторами, ассоциированными со строками и столбцами матрицы, элементы которой представляют уровни главного фактора. Предположим, например, что этот план имеет такое же число столбцов, как и уровней, но меньшее число строк, чем столбцов. Каждый уровень появится лишь один раз в каждой строке, что дает рандомизированный блочный план относительно строкового блочного фактора. Тем не менее, обращаясь к столбцовому блоковому фактору, получаем сбалансированный неполноблочн ы й план. Удаление четвертой строки из латинского квадрата 4 × 4 дает квадрат Юдена 3 × 4 .
Примеры
1 Преобразование латинского квадрата 4 × 4 в квадрат Юдена 3 × 4
|
Блоковый фактор 1 (строки) |
Блоковый фактор 2 (столбцы) |
|||
|
1 |
2 |
3 |
4 |
|
|
1 |
А |
D |
C |
В |
|
2 |
В |
А |
D |
C |
|
3 |
С |
В |
А |
D |
|
|
|
|
|
|
где А, В, С и D - четыре уровня главного фактора;
А , В, С, D - уровни
фактора , удаленные из латинского квадрата.
2 Следующее расположение цифр описывает квадрат Юдена 4 × 7 :
3 4 5 6 7 1 2
5 6 7 1 2 3 4
6 7 1 2 3 4 5
7 1 2 3 4 5 6
В этом примере видны строки из рандомизированного блочного плана и столбцы из сбалансированного неполноблочного плана с параметрами l = b = 7, h = k = 4 и λ = 2 .
К термину «План с расщеплен н ой делян кой» ( 2.3.6)
Пример - Три варианта фактора А испытывают в двух повторениях. В каждом варианте фактора А изучают два одинаковых варианта фактора В.
|
Делянка |
Повторение 1 |
|
Повторение 2 |
||
|
А1 |
А1 В2 |
А1 В1 |
А1 В2 |
А1 В1 |
|
|
А2 |
А2 В1 |
А2 В2 |
А2 В1 |
А2 В2 |
|
|
А3 |
А3 В1 |
А3 В2 |
А3 В1 |
А3 В1 |
|
В этом примере повторения играют роль блоков для первого этапа главного фактора А и каждая делянка, связанная с одним из трех вариантов А, играет роль блоков на втором этапе дополнительного главного фактора В (фактор внутри делянки), изучаемого внутри варианта фактора А . Следовательно, ошибка опыта для фактора В внутри делянки должна быть меньше, чем для всего эксперимента. В плане с расщепленной делянкой получают разные меры остаточной ошибки для эффектов внутри делянки и между делянками. Можно обобщить такой план дальше за счет включения фактора третьего этапа в варианты фактора второго этапа. План такого типа часто используется, когда долговременные или крупномасштабные опыты проводятся с уровнями фактора, которые нелегко изменяются, а остальные факторы могут меняться без проблем в ходе опыта или на большой площади.
Такой тип расположения факторов обычен для промышленного экспериментирования, как, впрочем, и для сельскохозяйственного (откуда и пришло само название). Часто одна серия обработок требует большой партии исходного материала для эксперимента, в то время как остальные можно сравнивать на малых количествах. Например, сравнение различных типов металлургических печей , используемых для производства некоторого сплава, потребует большего количества сплава, чем сравнение разных типов литейных форм, в которые можно заливать этот сплав. Типы печей рассматривают как варианты фактора первого этапа, а варианты форм - как варианты фактора второго этапа (внутри делянки). Другой пример - большой станок, скорость которого можно поменять только заменив редуктор, что долго и дорого, поэтому желательна редкая перемена этого фактора. Но материал, обрабатываемый на данном станке на каждом этапе, можно подвергать различным способам термообработки, формовать при разных давлениях и полировать с помощью различных полировальных составов, то есть эти факторы относительно просто переводить с одного уровня на другой. Они и образуют факторы внутри делянки (факторы второго этапа), тогда как изменение скорости - это фактор между делянками (или фактор первого этапа).
К термину «Дву хфакт орны й план с расщепленной делянкой» ( 2.3.7)
Пример - Для плана 3 × 4 подходящие расположения после рандомизации могут выглядеть так:
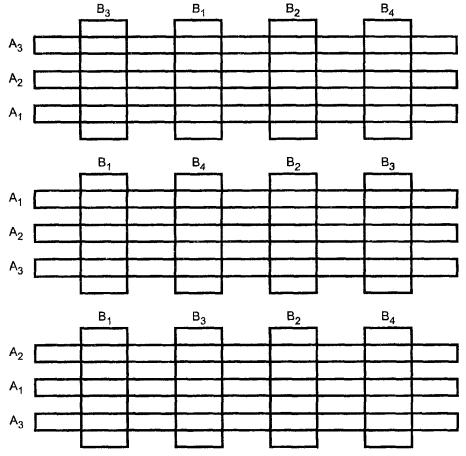
План с д вусторонн е расщепленной делянкой приводит к меньшей точности определения главных эффектов А и В, но обеспечивает большую точность измерения взаимодействий. Последние, как правило, определяются точнее, чем в рандомизированных блочных или обычных планах с расщепленной делянкой.
В промышленном экспериментировании их использование иногда неизбежно. Например, в текстильной промышленности фактором А могут быть различные методы отбеливания перокс ид ом хлора, а фактором В - различные количества перекиси водорода в процессе охлаждения.
К термину «План п оверхности отклика» ( 2.4)
Преимущество использования плана поверхности отклика заключается в том, что он предлагает поправку к предсказывающим переменным (которые по предположению непрерывны), что позволяет получать «улучшенные» отклики.
Примеры
1 Ниже приведены данные центрального композиционного плана. Это набор обработок, состоящий из кубических, звездных и центральной точек, выбран так, чтобы получить эффективный план (обычно ротатабельный). Для трех предикторов приведенный ниже набор образует центральный композиционный план.
Экспериментальные единицы x 1 x 2 x 3
1 -1 -1 -1
2 1 -1 -1
3 -1 1 -1
4 1 1 -1
5 -1 -1 1
6 1 -1 1
7 -1 1 1
8 1 1 1
9 0 0 0
10 0 0 0
11 -2 0 0
12 2 0 0
13 0 -2 0
14 0 2 0
15 0 0 -2
16 0 0 2
Экспериментальные единицы 1 - 8 образуют кубическую часть плана, эквивалентную факторному плану 23. Уровни предсказывающих переменных даны в кодированных значениях.
Экспериментальные единицы 9 и 10 - это обработки в центральных точках, а 11 - 16 - в звездных. Предполагают, что сначала можно реализовать первые 8 опытов, а затем выполнить остальные. Действительный порядок обработок надо ранд омизировать. Центральный композиционный план облегчает последовательную «сборку» компонентов плана. Подобранная по данным, полученным из эксперимента, модель может состоять из линейной ( x 1 , x 2 , x 3 ), квадратичной ( x 2 1 , x 2 2 , x 2 3 ) моделей и дв у хфак торны х взаимодействий ( x 1 x 2 , x 1 x 3 , x 2 x 3 ).
Распространенный вариант центрального композиционного плана состоит в использовании меньшего числа уровней факторов, это так называемый «сжатый» центральный композиционный план, получаемый выбором α = 1 для всех звездных точек. Меньшее число уровней факторов может привести к потере ротатабельности (в зависимости от числа факторов).
2 План Бокса-Бенкена получают соот ветствующей комбинацией факторного плана 2 k с сбалансированным неполноблочн ы м планом. Следующий набор образует план Бокса-Бенкена для трех переменных x 1 , x 2 , x 3.
Экспериментальные единицы x 1 x 2 x 3
1 0 -1 -1
2 0 1 -1
3 0 -1 1
4 0 1 1
5 -1 0 -1
6 1 0 -1
7 -1 0 1
8 1 0 1
9 -1 -1 0
10 1 -1 0
11 -1 1 0
12 1 1 0
13 0 0 0
14 0 0 0
15 0 0 0
3 Пятиугольный план - это дву хфакторны й план, в котором точки плана - это 5 равномерно расположенных на единичной окружности точек (используя кодированные уровни переменных) и, возможно дублированных, центральных точек. Набор 5 точек, удовлетворяющих этому условию, следующий: (1 ; 0 ), (0 ,309 ; 0 ,951 ), (-0 ,809 ; 0 ,588 ), (-0 ,809 ; -0 ,588 ), (0 ,309 ; -0 ,951 ). Отметим, что cos 72 ° = 0 ,309 , sin 72 ° = 0 ,951 и т.д.
4 Шестиугольный план - э то двухфакторный план, в котором точки плана - это 6 равномерно расположенных на единичной окружности точек (используя кодированные уровни переменных) и, возможно дублированных, центральных точек. Набор 6 точек, удовлетворяющих этому условию, следующий: (1 ; 0 ), (0 ,5 ; 0 ,866 ), (-1 ; 0 ), (-0 ,5 ; -0 ,866 ). Отметим, что cos 60° = 0 ,5 ; sin 60 ° = 0 ,866 и т.д.
Любой правильный многоугольник, вписанный в окружность единичного радиуса, может служить основой ротатабельного плана в классе планов поверхностей отклика.
К термину «План для смесей» ( 2.5)
Факторы, описывающие содержание доли металлов в сплаве, - типичный пример плана для смесей. Пространство плана должно удовлетворять условию X 1 + X 2 + , …,+ Xk = 1.
Специальные планы применимы при наличии дальнейших ограничений, например при минимизации доли выбранных факторов.
К термину «( Гнездовой) эксперимент с группировкой» ( 2.6)
Такие планы обычно используют для оценки компонентов дисперсии рассматриваемых факторов. В случае трех факторов А, В, С каждый уровень фактора В появляется только при одном уровне фактора А, а каждый уровень фактора С появляется только при одном уровне фактора В. Эксперимент с группировкой для k -фа к торов, где k ≥ 2 , еще называют k -с туп енчаты м экспериментом с группировкой.
Пример - Рассмотрим ситуацию, когда три различных поставщика предоставляют по 4 партии сырья компании, которая последовательно анализирует их на чистоту (рисунок А.2).
Рисунок А. 2 - Иллюстрация примера
Как видно из рисунка А.2, партии сгруппированы по поставщикам, так как партия 1 от первого поставщика отличается от партии 1 от второго поставщика. Хотя номер партии тот же самый, факторы партии и поставщика не пересекаются. Этот пример даст план с группировкой и в том случае, если каждый поставщик поставляет разное число партий. Следующий рисунок А.3 так же описывает эксперимент с группировкой.
Рисунок А .3 - Иллюстрация эксперимента с группировкой
Анализ намного упрощается в том случае , если число партий от каждого поставщика одинаково.
Как правило, эксперименты с группировкой используют в терминах компонент, дисперсии, а не в терминах различия уровней отклика или прогнозирующих моделей.
К термину «Сбалансированный (гнездовой) эксперимент с группировкой» ( 2.6.1)
Пример - На рисунке А.4 изображен сбалансированный эксперимент с группировкой.
Рисунок А. 4 - Сбалансированный (гнездовой) эксперимент с группировкой
Указанный эксперимент - это сбалансированный план с группировкой, поскольку каждая лаборатория тратит два дня (число уровней фактора В равно 2), а два результата измерения получают в каждой лаборатории за день (число уровней фактора С равно 2). Дни, используемые лабораториями, скорее всего будут разными, так как они по предположению были выбраны случайным образом из некоторого интервала.
Иногда допускается изменить определения уровней фактора таким образом, чтобы стало возможным сравнить их с другими факторами для получения более полной информации. B 1 может быть назначен на понедельник, а B 2 - на пятницу. Следовательн о, результаты, полученные в понедельник, можно сравнивать с результатами, полученными в пятницу. И, следовательно, для всех лабораторий это будет общим, в отличие от ситуации, рассмотренной выше, где назначения дней были не связаны. В этом случае мы получаем пересекающуюся (то есть каждый уровень фактора используют со всеми уровнями другого фактора), а не иерархическую классификацию и, следовательно, ее можно рассматривать как факторный эксперимент.
К термину «Нерегулярный (гнездовой) эксперимент с группировкой» ( 2.6.2)
Для нерегулярного эксперимента с группировкой все эффекты факторов оценивают приблизительно с тем же числом степеней свободы.
Пример - На рисунке А.5 изображен нерегулярный эксперимент с группировкой.
Рисунок А .5 - Уступчатый гнездовой эксперимент
К термину «Оптимальный план» ( 2.7)
При оптимизации определенного критерия следует отметить, что получаемый оптимальный план зависит от корректности принятой модели. Если эта модель неверна, то полученный план может быть теоретически (то есть математически) оптимальным, но практически он бесполезен.
К термину «Матрица плана» ( 2.7.1)
Индивидуальные обработки, составляющие строки матрицы плана, могут быть уже преобразованы в соответствии с постулируемой моделью.
Для данного плана эксперимента можно построить несколько матриц плана в зависимости от постулируемой модели.
Матрицу плана или модели обычно обозначают как X . Каждая строка X соответствует одной обработке. Первый столбец X может состоять из единиц, если общее среднее , например μ , присутствует в модели. Другие столбцы могут обозначать факторы или функции предсказывающих переменных.
К термину « D -оп ти мал ьны й план» ( 2.7.1.1)
Критерий D -оптима л ьного плана определяется объемом доверительного эллипсоида коэффициентов, связанных с матрицей плана X . Планы Пла кк етт а-Берман а из 2 .2 D -оп ти мал ьны относительно модели главных эффектов.
К термину « А-оп тимал ьны й план» ( 2.7.1.2 )
Критерий А-оптима л ьного плана объединяет меру объема доверительного эллипсоида и степень его сферичности.
К термину « G -оп т им ал ьны й план» ( 2.7.1.3)
Оптимальность данного плана не зависит явно от матрицы X . Можно доказать, что при некоторых условиях критерии D - и G -оптима л ьны х планов эквивалентны, так что можно использовать G -критерий, обеспечивающий процесс оптимизации для получения D -оптимального плана.
К термину «Ортогональ н ый план» ( 2.8)
Пара факторов ортогональна, если она удовлетворяет условию
nij = ( ni × nj ) /N
для каждой комбинации уровней ( i , j ) и каждой пары столбцов;
где nij - число появлений комбинации уровня ( i , j ) в любых двух столбцах;
ni - число появлений уровня i в одном столбце;
nj - число появлений уровня j в другом столбце;
N - общее число экспериментальных единиц.
К термину «Насыщенный план» ( 2.9)
Невозможно однозначно определить больше параметров, чем число экспериментальных единиц данного плана.
К термину «Графический метод» ( 3.1)
Простые графики могут представить начальную, но эффективную оценку результатов спланированного эксперимента.
К термину «График главных эффектов» ( 3.1.1)
Пример - Рисунок А.6 дает пример графика главных эффектов. Отклик - степень конверсии (в процентах ), а предсказывающие переменные - количество катализатора (А), температура (В), давление (С) и концентрация ( D ). Каждый предиктор был задан на двух уровнях, о б означенных как «-» - низкий и « +» - высокий. Таким образом был проведен полный факторный эксперимент 24. Из рисунка видно, что температура влияет на конверсию сильнее остальных предсказывающих переменных. Влияние катализатора стоит на втором месте, а влияние других двух факторов сравнимо и незначительно. Следует провести дополнительный анализ, чтобы определить, насколько наклон соединяющих линий на графике значимо отличается от нуля.
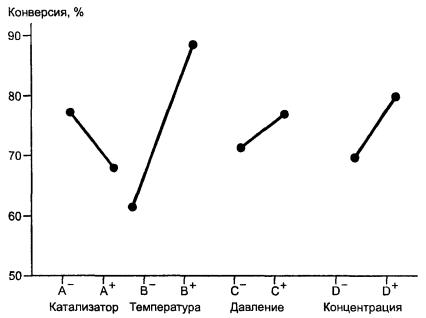
Рисунок А. 6 - График главных эффектов
График главных эффектов дает средний отклик на различных уровнях каждого фактора. Характер и величина влияния каждого фактора на отклик ясны из графика. Наличие взаимодействий может скрыть влияние различных факторов.
К термину «График взаимодействий» ( 3.1.2)
График взаимодействий дает инструмент для обнаружения и интерпретации взаимодействий. Отсутствие параллелизма на графике указывает на эффект взаимодействи я.
К термину «График квантилей эффектов» ( 3.1.3)
Пример - На рисунке А.7 представлены данные, взятые из примера к термину «график главных эффектов» ( 3.1.1).
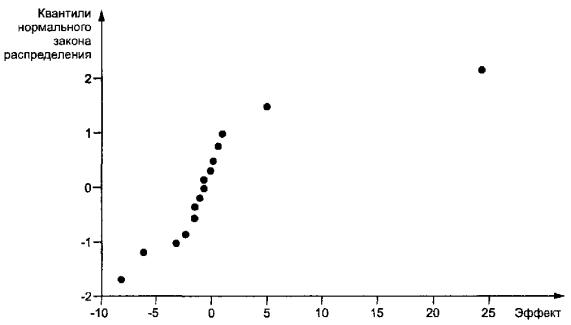
Рисунок А. 7 - График квантилей эффектов
Для экспериментов без повторений этот график может подсказать доминирующие эффекты (то есть те точки, которые лежат далеко вправо или далеко влево от «руководящей» линии, проходящей через массу нанесенных на график точек. На этом рисунке верхняя правая точка со значением, равным 5 , соответствует эффекту температуры.
К термину «График остатков» ( 3.1.4)
Пример - Продолжим рассмотрение примера к термину «график главных эффектов» ( 3.1.1). Используем модель с четырьмя главными эффектами и взаимодействием BD , где В - температура, D - концентрация. График остатков представлен на рисунке А.8.
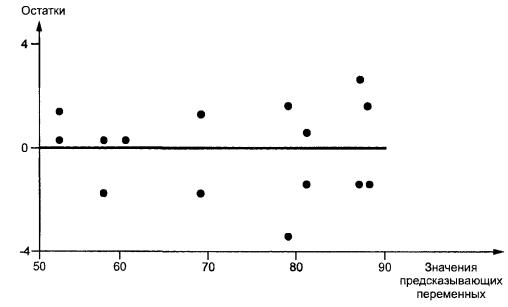
Рисунок А. 8 - График остатков
К термину «Метод наименьших квадратов» ( 3.2)
Ошибки эксперимента, связанные с отдельными наблюдениями, обычно предполагаются независимыми, хотя методы статистических выводов могут быть скорректированы с учетом корреляции ошибок. Обычный дисперсионный анализ, регрессионный анализ и ковариационный анализ - все основаны на методе наименьших квадратов и обладают различными преимуществами при вычислениях и интерпретации результатов, связанных со степенью некоторых балансов в расположениях экспериментов, которые допускают удобные группировки данных.
К термину «Регресс и онный анализ» ( 3.3)
Регрессионный анализ обычно связывают с процессом оценивания параметров постулируемой модели с помощью оптимизации значения целевой функции (например, минимизируя сумму квадратов разностей между наблюдаемыми откликами и предсказанными по модели). Существующее статистическое программное обеспечение, устранив большинство проблем, связанных с получением оценок параметров и их стандартных ошибок, содержит немало моделей диагностики. Регрессионный анализ также облегчает рассмотрение других мер для отклика. Например, если нас интересует дисперсия в факторном эксперименте с повторениями, то отклик логарифм Si 2 (где S 2 - выборочная дисперсия по параллельным точкам) может быть проанализирован и интерпретирован легче, чем сами отклики.
Регрессионный анализ играет роль, сходную с дисперсионным анализом, и особенно подходит для случая, когда уровни факторов непрерывны и важна явная предсказывающая модель. Регрессионный анализ можно также использовать в экспериментах с пропущенными данными в отличие от дисперсионного анализа, который требует сбалансированных данных. Однако потеря баланса увеличивает зависимость от порядка (общие элементы включаются в первый коррелированный член, а не в последующие члены проверок гипотез ), а также ведет к потере других преимуществ сбалансированного эксперимента. Для сбалансированных экспериментов обе методики - варианты метода наименьших квадратов, и они дают сравнимые результаты.
Пример - Рассмотрим ортогональный план с тремя факторами в факторном эксперименте 23 без повторений. Для экспериментальной единицы постулируется следующая модель:
Y = β 0 x 0 + β 1 x 1 + β 2 x 2 + β 3 x 3 + e ,
где x 0 = 1 ;
β 0 , β 1 , β 2 , β 3 - коэффициенты регрессии;
x 1 - уровень фактора А;
x 2 - уровень фактора В;
x 3 - уровень фактора С;
e - случайная ошибка.
Эту модель можно применить и для трех качественных факторов, уровни которых закодированы как -1 и +1 .
В таблицах А.7 и А.8 представлен регрессионный анализ для данного примера.
Таблица А. 7 - Регрессионный анализ для примера 1
|
Источник вариации |
Коэффициент регрессии |
Сумма квадратов |
Степень свободы |
Средний квадрат |
|
Всего |
- |
S T = ΣYi 2 |
8 |
- |
|
Постоянный ( X 0 ) |
|
Sx 0 = β 0 Σx 0 i Yi |
1 |
Sx 0 |
|
Регрессия на X 1 ( A ) |
|
Sx 1 = β1Σx1iYi |
1 |
Sx 1 |
|
Регрессия на X 2 (В) |
|
Sx 2 = β2Σx2iYi |
1 |
Sx 2 |
|
Регрессия на X 3 ( С ) |
|
Sx 3 = β 3 Σx 3 i Yi |
1 |
Sx 3 |
|
Остаток |
- |
S E = S T - Sx 0 - Sx1 - Sx2 - Sx3 |
4 |
S E /4 |
|
Примечание |
||||
Если в одном блоке эксперимент 23 был повторен, то степени свободы для строки «всего» (строка 1 ) будут равны 16 , а для строки «остаток» будут равны 12 . «Остаточную» сумму квадратов можно тогда разделить на 2 части: одна связана с «повторениями», а вторая - с «неадекватностью» и со степенями свободы 8 и 4 соответственно.
Таблица А. 8 - Дополнительные действия для эксперимента с повторениями
|
Источник вариации |
Сумма квадратов |
Степени свободы |
Средний квадрат |
F |
Ожидаемое |
|
Остаток |
S E |
12 |
S E /12 |
|
|
|
Повторения |
|
8 |
S E /8 |
|
|
|
Неадекватность |
S L = S E - S R |
4 |
S L /4 |
|
|
Статистическую значимость каждого источника можно проверить, используя F - стати стику для среднего квадрата этого источника и соответствующее значение ошибки, если подходит предположение о нормальности распределения. Для ситуации без повторений «остаточный» член сравнивается с регрессионным. Для ситуации с двумя повторениями член «неадекватность» сравнивается с «повторениями» («ошибка эксперимента») для определения, адекватна ли модель. «Повторение» представляет меру ошибки эксперимента, свободной от возможного вклада от неадекватности модели, который может смешиваться с «остатком».
К термину «Дисперсионный анализ» ( 3.4)
Дисперсионный анализ облегчает оценивание компонент дисперсии и проверку гипотез о параметрах модели. Таблица дисперсионного анализа обычно содержит столбцы для:
- источника вариации;
- сумм квадратов ( SS );
- степеней свободы ( DF );
- средних квадратов ( MS ) (сумм квадратов, деленных на число степеней свободы);
- F (отношения средних квадратов в строке к среднему квадрату, связанному с ошибкой );
- ожидаемых средних квадратов E ( MS ) (математического ожидания суммы квадратов данных в терминах параметров модели).
Строки таблицы представляют определенные эффекты факторов или взаимодействия, блоки (если в эксперименте применялось блокирование) или ошибки (остаточные эффекты, не учтенные моделью или блоками). Строка, обозначенная «всего», обычно содержит общую сумму квадратов относительно общего среднего и основана на числе степеней свободы, которое на единицу меньше, чем объем выборки.
Пример
Рассмотрим рандомизированный блочный план, в котором наблюдения получены с i - го уровня из l уровней фактора А в j -м блоке из h ; обозначены как: Yij = ( I = 1 , 2 , …, l ; j = 1 , 2 , …, h ). Основной фактор А обозначает постоянный эффект обработки; фактор В представляет постоянный эффект блока. Тогда выполняется следующая таблица А.9 дисперсионного анализа:
Таблица А. 9 - Дисперсионный анализ для примера
|
Источник вариации |
Сумма квадратов ( SS) |
Степени свободы ( DF ) |
Средний квадрат ( MS ) |
F |
Ожидаемый средний квадрат [ E ( MS )] |
|
Всего |
|
v T = hl - 1 |
- |
- |
- |
|
Фактор А (обработка) |
|
v A = l - 1 |
|
|
σ 2 + hK 2 A |
|
Фактор В (блок) |
|
v B = h - 1 |
|
|
σ2 + lK2B |
|
Ошибка |
|
v e = ( l - 1 )( h - 1 ) |
|
- |
σ 2 |
В таблице А.9:
S T = S A + SB + Se ;
v T = v A + vB - ve ;
F ( v A , v e ), F ( v B , v e ) - F -статистики.
Одна модель, связанная с наблюдениями, имеет следующий вид
Yij = μ + αi + βj + е ij ; i = 1 , 2 , …, l ; j = 1 , 2 , …, h ,
где Σα i = Σ βi = 0; eij ~ N ( 0 , σ 2 );
![]()
![]()
где μ - общее среднее;
αi - эффект i -й обработки;
βi - эффек т j -го блока;
eij - ошибка эксперимента;
σ 2 - дисперсия случайной величины;
N(0 , σ 2 ) - нормированное нормальное распределение с параметрами (0 , σ 2 ).
В этом примере предполагают, что назначены постоянные уровни. Оценки метода наименьших квадратов для μ , αi , βi и σ 2 получают по следующим формулам:
![]()
![]()
![]()
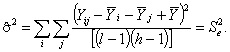
Формулы этого примера упрощенные, так как в рандомизированном блочном плане каждая ячейка должна содержать одинаковое число наблюдений.
Основы предположения дисперсионного анализа: эффекты всех источников вариации аддитивны и экспериментальные ошибки независимы и имеют нормальное распределение со средним, равным нулю, и равными дисперсиями. Этот метод вместе с F -отношением используется для проверки значимости этих источников вариации и для получения оценки дисперсии, связанной с этими источниками. Предположение о нормальности распределения необходимо только для этой проверки значимости и для вычисления доверительных интервалов. Средние арифметические и взаимодействия обычно получают суммированием в таблицах сопряженности с двумя (или k ) уровнями. Этот пример предполагает модель 1 (модель постоянных эффектов). Когда предположение о нормальности ошибок не проходит, допускается использовать преобразования (например логарифмирование) откликов или применять непараметрические процедуры.
К термину «Модель дисперсионного анализа с постоянными эффектами» ( 3.4.1)
При постоянных уровнях нельзя вычислить компоненты дисперсии. Эту модель также иногда называют «моделью 1 -го дисперсионного анализа».
К термину «Модель дисперсионного анализа со случайными эффектами» ( 3.4.2)
Случайные уровни в основном интересны при получении оценок компонентов дисперсии. Эту модель обычно называют «моделью 2 -го дисперсионного анализа».
Пример - Рассмотрим ситуацию, когда в процессе обрабатываются партии сырья.
Партию можно рассматривать как случайный фактор, когда несколько партий случайным образом выбраны из совокупности партий.
К термину «Смешанная модель дисперсионного анализа» ( 3.4.3)
Компоненты дисперсии имеют смысл только для случайных факторов. Более того, оценки эффектов применимы только для фиксированных факторов. Эту модель также называют «модель 3 -го дисперсионного анализа».
К термину «Ковариационный анализ» ( 3.5)
Ковариационный анализ можно рассматривать как комбинацию регрессионного и дисперсионного анализов.
Обычно сопутствующий фактор нельзя учесть при планировании эксперимента и нежелательное влияние на результаты приходится учитывать уже в анализе. Например, экспериментальные единицы могут различаться по количеству некоторого химического компонента от единицы к единице. Его можно измерить, но нельзя изменить.
Ключевые слова: статистические методы, эксперимент, план эксперимента, фактор, эффект, взаимодействие, отклик, опыты, регрессионный анализ, дисперсионный анализ