П 53-90 Рекомендации по прогнозированию деформаций сооружений гидроузлов на основе результатов геодезических наблюдений
МИНИСТЕРСТВО ЭНЕРГЕТИКИ И ЭЛЕКТРИФИКАЦИИ СССР
ВСЕСОЮЗНЫЙ ОРДЕНА ТРУДОВОГО КРАСНОГО ЗНАМЕНИ
НАУЧНО-ИССЛЕДОВАТЕЛЬСКИЙ ИНСТИТУТ ГИДРОТЕХНИКИ
имени Б. Е. ВЕДЕНЕЕВА
РЕКОМЕНДАЦИИ
ПО ПРОГНОЗИРОВАНИЮ ДЕФОРМАЦИЙ
СООРУЖЕНИЙ ГИДРОУЗЛОВ
НА ОСНОВЕ РЕЗУЛЬТАТОВ
ГЕОДЕЗИЧЕСКИХ НАБЛЮДЕНИЙ
П 53-90
ВНИИГ
ЛЕНИНГРАД 1991
Применение Рекомендаций предусматривается при наблюдениях за тектоническими и техногенными деформациями земной поверхности в районах крупных гидроузлов, а также в процессе геодезического контроля за поведением водоподпорных сооружений и агрегатных блоков зданий строящихся и эксплуатируемых ГЭС.
Рекомендации предназначены для сотрудников предприятий и экспедиций ГУГК СССР, выполняющих работы на геодинамических полигонах ГЭС, а также для сотрудников проектно-изыскательских экспедиций Минэнерго СССР, технических руководителей гидроцехов ГЭС, инженеров-гидротехников и инженеров-математиков, занимающихся моделированием наблюдаемых процессов деформаций сооружений ГЭС.
Разработка Рекомендаций выполнена во Всесоюзном производственном объединении «Инженерная геодезия» и в Алтайском политехническом институте Минвуза РСФСР коллективом авторов: доктором техн. наук Ю.П. Гуляевым, канд. техн. наук Е.А. Васильевым при участии канд. техн. наук А.Б. Васильева (раздел 3). Программное обеспечение разработано Л.А. Васильевой, М.В. Крайвановой, канд. техн. наук А.Д. Слободяном. Общее редактирование Рекомендаций выполнено Н.С. Чирятьевым.
Содержание
|
1. ВВЕДЕНИЕ 2. ОБЩИЕ ПОЛОЖЕНИЯ 3. ТРЕБОВАНИЯ К ИСХОДНЫМ ДАННЫМ ДЛЯ ПРОГНОЗИРОВАНИЯ 4. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПРОЦЕССА ДЕФОРМАЦИЙ, ОСНОВЫ ИХ ПОСТРОЕНИЯ И ПРИМЕНЕНИЯ 5. МЕТОДОЛОГИЧЕСКИЕ ПРИНЦИПЫ ПРОГНОЗИРОВАНИЯ Приложение 1 ПОЯСНЕНИЕ ИСПОЛЬЗУЕМЫХ ТЕРМИНОВ 1 Приложение 2 ПРИМЕР ПОСТРОЕНИЯ КИНЕМАТИЧЕСКОЙ МОДЕЛИ ПРОЦЕССА ОСАДКИ НА НИЖНЕКАМСКОЙ ГЭС И ВЫПОЛНЕНИЯ ПРОГНОЗИРОВАНИЯ Приложение 3 ПРИМЕР ПОСТРОЕНИЯ КОМПЛЕКСНОЙ ДИНАМИЧЕСКОЙ МОДЕЛИ ДЛЯ ПРОГНОЗИРОВАНИЯ ПРОЦЕССА ГОРИЗОНТАЛЬНОГО ПЕРЕМЕЩЕНИЯ ГРЕБНЯ ПЛОТИНЫ КРАСНОЯРСКОЙ ГЭС НА СЕКЦИИ № 22 Приложение 4 ПРИМЕР ИСПОЛЬЗОВАНИЯ ТАБЛИЦ ДЛЯ НАХОЖДЕНИЯ КРАТКОСРОЧНОГО ПРОГНОЗА И ОЦЕНКИ ЕГО ТОЧНОСТИ Приложение 5 ОПИСАНИЕ КОМПЛЕКСА ПРОГРАММ ПРОГНОЗИРОВАНИЯ ДЕФОРМАЦИЙ ОБЩИЕ СВЕДЕНИЯ
|
1. ВВЕДЕНИЕ
В Рекомендациях изложены основные принципы и методика прогнозирования наблюдаемых геодезическими методами процессов вертикальных и горизонтальных перемещений деформационных знаков, заложенных в сооружения ГЭС. Поскольку по этому виду работ предварительно не разрабатывались основные положения и инструкции, то они и нашли свое отражение в Рекомендациях.
Настоящие Рекомендации основываются на положениях прогностики, на теории динамических систем, теории случайных функций, теории статистического оценивания и требуют от пользователя соответствующей подготовки. В целях повышения доступности материала при его изложении даются необходимые исходные понятия, допускаются упрощенные описания и приводится в Приложении 1. пояснение используемой терминологии. В этих же целях математические модели демонстрируются в общей и наиболее понятной форме, а технология оценивания параметров моделей и прогнозирования показывается в приложениях на примере наиболее простых моделей. Такой характер представления материала позволяет читателю освоить на простых моделях технологию прогнозирования и использовать ее при построении более сложных моделей, которые можно осуществить лишь на ЭВМ. С этой целью разработано соответствующее программное обеспечение для ЕС ЭВМ. Описание программ и инструкция по их использованию даются в Приложении 5. Дополнительные сведения по программам, а также тексты исходных модулей могут быть получены по адресу: г. Новосибирск, Красный проспект, 35, НИИПГ.
|
Главное управление геодезии и картографии при СМ СССР и Министерство энергетики и электрификации СССР |
Рекомендации по прогнозированию деформаций сооружений гидроузлов на основе результатов геодезических наблюдений |
ВНИИГ П 53-90 |
2. ОБЩИЕ ПОЛОЖЕНИЯ
2.1. Объектом прогнозирования 1 (здесь и далее цифры сносок - порядковые номера терминов, приведенных в Приложении 1) является процесс деформации основания и несущих конструкций гидротехнического сооружения. Все изучаемые виды деформаций выражаются через линейные вертикальные и горизонтальные перемещения наблюдаемых, геодезических знаков, заложенных в характерных местах так, чтобы по значениям перемещений можно было вычислить любой необходимый конкретный вид деформации.
Прогнозирование производится на основе результатов геодезических наблюдений за деформациями статистическим методом прогнозной экстраполяции 2 и может выполняться с помощью кинематических или динамических моделей в зависимости от полноты и вида имеющихся исходных данных. Кинематические модели отражают зависимость величин деформаций от времени, а динамические модели описывают процессы деформаций с учетом совместного влияния времени и главных возмущающих факторов. Следовательно, кинематические модели строятся только по геодезическим данным, динамические модели по количественным данным комплексных натурных наблюдений.
2.2. Эндогенной переменной 3 объекта прогнозирования служит величина перемещения, получаемая из геодезических наблюдений в форме динамического ряда. 4 Геодезические данные рассматриваются как дискретное представление непрерывного случайного процесса, за отдельные реализации которого принимаются изменяющиеся от времени значения перемещения каждой наблюдаемой точки, а за сечение - случайная величина перемещения в данном цикле наблюдений. Таким образом, значения перемещений всех наблюдаемых деформационных знаков образуют семейство реализаций) случайного процесса, по которому можно в каждом цикле наблюдений установить эмпирический закон распределения случайной величины перемещения, а по распределению случайной величины перемещения в ряде циклов наблюдений - определить закон распределения случайного процесса перемещения. В результате будет получена наиболее полная математическая модель наблюдаемого процесса перемещения, которая может быть выражена через характеристики случайного процесса.
|
Внесены Всесоюзным производственным объединением «Инженерная геодезия» и ВНИИГом им. Б.Е. Веденеева |
Утверждены решением ВНИИГ им. Б.Е. Веденеева № 19 от 15.06.90 по согласованию с Главным управлением геодезии и картографии при СМ СССР |
Срок введения III кв. 1991 г. |
Эндогенная переменная в динамической модели является выходной переменной 5. При этом в построенной на основе геодезических данных динамической модели в качестве выходной переменной может использоваться не только процесс перемещения, но и связанный с ним функционально какой-либо другой наблюдаемый процесс, характеризующий напряженно-деформированное состояние конструкций сооружения.
2.3. В кинематических моделях за экзогенную переменную 6 принимается фактор времени, а к прогнозному фону 7 относятся инженерно-геологические, конструктивные, строительно-эксплуатационные и другие условия работы сооружений. Влияние прогнозного фона учитывается априорно при выборе периодов основания прогноза 8 и упреждения 9 , так чтобы оба периода схватывали одинаковую природу развития процесса деформации. В динамических моделях экзогенной переменной служат наряду с фактором времени наблюдаемые факторы прогнозного фона, используемые апостериорно в виде входных воздействий 10 .
При использовании кинематических моделей их гибкое реагирование на изменения, происходящие в объекте прогнозирования, должно обеспечиваться за счет выполнения принципа непрерывности прогнозирования 11 с учетом дисконтирования информации 12. Для динамических моделей также следует соблюдать принцип непрерывности, однако способность гибкого реагирования на изменения входных воздействий заложена в самих динамических моделях, и необходимость их корректировки возникает лишь в случаях недопустимого возрастания фактических ошибок прогноза 13 на контрольных периодах упреждения. 14
2.4. Прогнозирование деформаций гидротехнических сооружений, выполняемое на основе геодезических данных, обеспечивает получение всех предусмотренных современной прогностикой видов прогнозов: поискового 15 , нормативного 16 , интервального 17 , точечного 18 , оперативного 19 , краткосрочного 20 , среднесрочного 21 , долгосрочного 22 , дальнесрочного 23 . При этом продолжительность периодов упреждения прогнозов различной срочности в основном согласуется с принятой для других видов объектов.
Поисковое и нормативное прогнозирование должно осуществляться в целях своевременного принятия мер, повышающих надежность, долговечность гидротехнических сооружений, обеспечивающих безопасность их эксплуатации, а также для оптимизации объемов геодезических наблюдений за деформациями сооружений. Нормативное прогнозирование позволяет при этом получать оценки возможных сроков стабилизации осадок и других видов деформации сооружений, устанавливать путем моделирования 24 критерии допустимых значений наблюдаемых перемещений при данном состоянии сооружения в естественных условиях экстремального воздействия факторов, вызывающих перемещения.
С помощью прогнозной модели 25 в виде двух первых условных моментных функций случайного процесса 26 наблюдаемого перемещения достигается сочетание интервального и точечного прогнозов. Условное математическое ожидание, определяемое по плотности распределения случайного процесса, позволяет находить наилучшие прогнозы значений перемещения каждого наблюдаемого деформационного знака из числа включений в модель, а по условной корреляционной функции, отражающей рассеивание плотности условного распределения, можно предвычислить точность прогнозов 27.
2.5. Ошибки прогнозов и правильность предвычисленной точности прогнозов зависит прежде всего от продолжительности периодов упреждения и согласованности этих периодов с выбранными периодами основания прогноза. При этом существенное влияние оказывают сопутствующие факторы, такие, как условия функционирования сооружения, полнота и точность информации о будущем развитии прогнозного фона, а также вид применяемой математической модели. Например, на эксплуатируемых плотинах ГЭС для сезонных перемещений, имеющих инерционное запаздывание 28 продолжительностью до 5- 6 месяцев, можно выполнять с помощью динамических моделей краткосрочное прогнозирование по фактическим значениям входных воздействий. Для этого при построении моделей нужно ввести транспортное запаздывание 29 , заменяющее часть инерционного запаздывания, описываемого моделью. В результате такого подхода ошибки прогнозов будут незначительно превышать ошибки измерений и согласовываться с предвычисленной точностью прогнозов, что позволит сократить объем наблюдений, заменив их выборочно контролируемыми прогнозами.
На периодах упреждения среднесрочного прогнозирования можно достичь приемлемой точности прогнозов с помощью кинематических моделей лишь при подборе трендов 30, адекватно отражающих будущее развитие описываемых процессов деформации, при условии неизменности прогнозного фона в части, не учитываемой трендом. Динамические модели позволяют получить необходимую точность среднесрочных прогнозов, если с достаточной точностью будут известны значения входных воздействий на периоде упреждения. Отмеченные особенности распространяются на долгосрочные и дальнесрочные прогнозы, причем ошибки прогнозов будут возрастать за счет изменения состояния сооружений, если эти изменения не учитываются адаптирующимися моделями.
2.6. Принцип верифицируемости 31 прогнозирования заключается в определении достоверности 32, точности и обоснованности прогнозов. Поскольку точность прогнозов наблюдаемых процессов перемещений предвычисляется в виде средних квадратических отклонений, то достоверность прогнозов составляет 0,68 или 0,95 соответственно для одинарного или удвоенного коридора погрешности 33. При этом предполагается, что процесс является нормальным 34 или нормализованным 35.
На данном этапе развития прогнозирования процессов деформации гидротехнических сооружений основным видом определения обоснованности прогнозов является инверсная верификация 36, осуществляемая путем проверки адекватности модели на периоде основания прогноза по остаточным ошибкам ее построения и на периоде контрольного упреждения по ошибкам прогнозов, по их согласованности с предвычисленной точностью прогнозов. Кроме того, можно проверять обоснованность прогнозов, получая их по моделям, построенным на периодах основания прогноза разной длины. Дополнительную верификацию можно производить в отдельных случаях, сравнивая результаты прогнозирования одного и того же процесса, полученные по кинематическим и динамическим моделям, а также прогнозы различных, но взаимосвязанных характеристик деформации.
2.7. Организация выполнения прогнозирования зависит от уровня обеспечения гидроцехов ГЭС современными ЭВМ и подготовленными специалистами. На данном этапе целесообразно осуществлять разработку прогнозов в научно-исследовательских организациях и передавать результаты для использования в гидроцеха ГЭС/ Результаты прогнозипования могут быть представлены в виде распечаток с ЭВМ. Содержащих прогнозы и характеристики их точности в табличной Форме, позволяющей быстро находить прогнозы для конкретных условий без применения ЭВМ; в виде выраженных графически критериев допустимых значений наблюдаемых перемещений, возможных при данном состоянии сооружения. В последующем развитии организация прогнозирования должна быть ориентирована на применение в гидроцехах микро-ЭВМ, а в дальнейшем - на включение прогнозирующей подсистемы в информационно-измерительную автоматизированную систему геодезического контроля за состоянием сооружений ГЭС.
Табличную форму прогнозов удобно использовать в эксплуатационный период для краткосрочного прогнозирования наблюдаемых перемещений, имеющих характер сезонных гармонических колебаний. Таблицы разрабатываются с помощью динамических моделей на многолетних периодах основания прогноза, которые охватывают различные условия работы сооружения при его установившемся состоянии. В Приложении 4 к Рекомендациям приводится пример подготовки таблиц и использования табличного метода прогнозирования горизонтального перемещения гребня плотины, даются характеристики ошибок и точности краткосрочных прогнозов, полученных по таблицам и проконтролированных наблюдениями.
2.8. Критерии допустимых значений наблюдаемых перемещений при данном состоянии сооружения, могут определяться в результате непосредственного прогнозирования на ЭВМ по динамическим моделям или с помощью таблиц для возможного в условиях нормальной эксплуатации сочетания максимальных влияний основных воздействующих факторов. Выход измеренных значений перемещений за границы установленных критериев будет служить сигналом об изменении состояния гидротехнического сооружения и потребует тщательного специального обследования условий функционирования сооружения. Дополнительным критерием будут служить фактические ошибки прогнозов, возрастание которых связано с изменением состояния сооружения и служит одновременно указанием к обновлению модели.
3. ТРЕБОВАНИЯ К ИСХОДНЫМ ДАННЫМ ДЛЯ ПРОГНОЗИРОВАНИЯ
3.1. Исходной информацией для прогнозирования деформаций гидротехнических сооружений и земной поверхности в районе гидроузла является аналитический обзор результатов повторных геодезических наблюдений, оформляемый в виде научно-технического отчета по отдельному циклу или группе циклов наблюдений.
3.2. Общие требования, структура и правила составления отчетов должны соответствовать ГОСТ 7.32-81*. «Система стандартов по информации, библиотечному и издательскому делу. Отчет о научно-исследовательской работе. Общие требования и правила оформления». Разъяснения основных положений ГОСТ 7.32-81* даны в «Методических указаниях для составления отчетов о научно-исследовательских работах» (М: ВНТИЦ, 1981).
3.3. В состав отчета должны быть включены титульный лист, реферат, введение, основная часть, заключение и список используемых источников. Основная часть должна состоять из двух подразделов:
а) характеристики геодезических работ в районе гидроузла (в том числе автоматизированных инженерно-геодезических наблюдений за плотиной и наблюдений за движениями земной поверхности, выполняемых также и методами геодезической астрономии и геодезической гравиметрии);
б) интерпретации результатов геодезических измерений.
3.4. В первом подразделе основной части отчета представляются по видам работ сведения об используемых приборах, методах и точности измерений, сведения о предварительной обработке и уравнивании результатов наблюдений в каждом цикле. Данные могут быть представлены как в табличном виде, так и на машинном носителе информации (магнитной ленте, магнитном диске, перфокартах).
Во втором подразделе должен быть обоснован метод подготовки исходных данных для интерпретации и прогнозирования. Деформации и перемещения должны быть представлены в виде графиков и картосхем.
3.5. Научно-технический отчет должен быть согласован:
а) в части наблюдений за движениями и деформациями земной поверхности района гидроузла - с территориальным научно-исследовательским институтом курирующим геофизические работы в данном регионе;
б) в части наблюдений за гидротехническими сооружениями - с отраслевым научно-исследовательским или проектным институтом, курирующим работы по строительству и эксплуатации данного гидроузла.
3.6. Кроме общих требований, изложенных в пп. 3.1 - 3.5, исходные данные должны соответствовать техническому проекту на геодезические работы, включающему производственную программу выполнения всех видов геодезических наблюдений.
Геодезические сети в районе гидроузла объединяются в специальный техногенный геодинамический полигон ГЭС (ТГП ГЭС). Властности, для прогнозирования движений и деформаций земной поверхности с применением динамических моделей исходные данные должны быть освобождены от систематического влияния внешних условий, кроме этого, внешние факторы условий должны быть сгруппированы и оценены для возможного выполнения корреляционного и факторного анализа.
3.7. Подробное описание исходных данных должно сопровождаться следующим:
а) по плановым сетям:
описанием физической природы внешних условий на ТГП ГЭС и методики их учета при геодезических наблюдениях (характеристикой природных процессов в системе плотина - водохранилище - окружающая среда, влиянием метеорологических факторов на измерение линий светодальномерами, влиянием метеорологических факторов на угловые измерения, влиянием техногенных факторов на линейные и угловые измерения);
описанием рекогносцировки геодезической сети, заложенных центров сети и построенных знаков;
описанием методики угловых измерений;
описанием методики линейных измерений;
обоснованием принятой периодичности измерений;
б) по высотным сетям:
описанием рекогносцировки нивелирных линий и закладки реперов;
описанием приборов для нивелирования и методики их поверки;
описанием методики выполнения геометрического, тригонометрического, гидростатического и гидродинамического нивелирования;
в) по астрономическим определениям:
описанием выбора мест расположения и закладки астро-пунктов;
описанием астрономических приборов, методики их поверки и исследования;
описанием методики выполнения астрономических определений на ТГП ГЭС;
г) по гравиметрическим определениям:
описанием выбора мест расположения и закрепления гравиметрических пунктов;
описанием гравиметрических приборов и методики их поверки;
описанием методики гравиметрических определений в теле плотины ГЭС;
описанием методики гравиметрических определений на земной поверхности в районе ТГП ГЭС;
описанием методики математической обработки результатов гравиметрических определений в теле плотины и на земной поверхности;
д) по учету влияния неприливных изменений силы тяжести на результаты геодезических и гравиметрических измерений на ТГП ГЭС:
описанием методики оценки прилегающей к гидроузлу области, в которой следует учитывать влияние изменения поля силы тяжести на результаты гравиметрических определений;
описанием методики оценки прилегающей к гидроузлу области, в которой следует учитывать влияние изменения уклонений отвеса на результаты геодезических измерений;
рабочими таблицами поправок за изменение силы тяжести для конкретных геодезических и гравиметрических пунктов, попадающих в область влияния;
рабочими картосхемами поправок для области влияния (в зависимости от изменения уровня водохранилища ГЭС);
е) по математической обработке результатов: описанием предварительной обработки результатов астрономических, гравиметрических, геодезических измерений на ТГП ГЭС-описанием применяемой методики уравнивания результатов астрономических, гравиметрических и геодезических измерений; каталогами уравненных координат и высот пунктов геодезических сетей (внутриплотинной и наземной) на каждый цикл измерений;
корреляционными матрицами координат и высот пунктов сетей по каждому циклу и группам циклов (матрицами шума для учета при прогнозировании);
ведомостями уравненных результатов геодезических наблюдений для каждого цикла наблюдений относительно начального цикла изменений горизонтальных направлений, изменений зенитных расстояний, изменений астрономических азимутов, изменений расстояний, изменений превышений, изменений силы тяжести;
ведомостями оценки точности уравненных величин для каждого цикла.
3.8. Прогнозирование движений и деформаций земной поверхности в районе гидроузла и гидротехнических сооружений может выполняться как с использованием исходных данных по всему комплексу работ на ТГП ГЭС, представленному в п. 3.7, так и с частичным объемом исходных данных, подготовленных по одному из видов измерений (плановых, высотных, гравиметрических) либо по одному из участков работ (только водохранилищная зона, только приплотинная зона, только внутриплотинные измерения).
4. МАТЕМАТИЧЕСКИЕ МОДЕЛИ ПРОЦЕССА ДЕФОРМАЦИЙ, ОСНОВЫ ИХ ПОСТРОЕНИЯ И ПРИМЕНЕНИЯ
4.1. Материал данного раздела рассчитан на обязательное применение программного обеспечения для построения математических моделей процесса перемещений и прогнозирования по ним. Разработанный комплекс программ обеспечивает возможность прогнозирования процесса перемещений на основе кинематических и динамических моделей. Подробное описание используемого при этом математического аппарата и описание комплекса программ приведены в Приложении 5.
4.2. При прогнозировании с помощью кинематической модели линейного 37 статистически однородного нормального случайного процесса перемещения для любой i - й реализации должна использоваться прогнозная модель, представленная в виде условного математического ожидания и условной корреляцион ной функции. Для построения модели в каждом цикле наблюдений, попадающем на период основания прогноза, находят по общеизвестным формулам статистические оценки: математическое ожидание, среднее квадратическое отклонение и коэффициент корреляции. Найденные методом наименьших квадратов статистические оценки аппроксимируются на периоде основания прогноза системой аналитических функций. Экстраполированные по полученным выражениям на период упреждения прогноза оценки математических ожиданий, средних квадратических отклонений и коэффициентов корреляции в сочетании с уравнениями условного математического ожидания и условного среднего квадратического отклонения позволяют получить прогноз перемещения i -й марки и характеристику точности прогноза.
4.3. В случаях, когда с помощью кинематической модели нужно описать нелинейный случайный процесс 38, предварительно выполняются аппроксимация нелинейного тренда (например, в виде экспоненты) и центрирование процесса 39. После этого для центрированной части процесса, т. е. по остаточным погрешностям аппроксимации, строится модель, описанная в п. 4.2. С помощью указанной модели производится прогнозирование и оценка точности, однако окончательные прогнозы находятся в результате сложения значений прогнозов центрированной части процесса, полученных по каждой реализации, со значениями тренда, экстраполированными на конец периода упреждения прогноза. Если изучаемый процесс перемещений не имеет нормального распределения, то предварительно выполняется его нормализация, затем делается вышеуказанное моделирование, а в заключение производится преобразование процесса, обратное нормализующему.
4.4. Полный алгоритм построения кинематической модели и прогнозирования по ней процесса перемещения содержит: проверку и формирование статистически однородных семейств реализаций процесса; проверку нормальности распределения процесса в целом и по каждому сечению периода основания прогноза; выполнение в необходимых случаях нормализующих преобразований; аппроксимацию и исключение нелинейного тренда в виде экспоненты или синусоиды; оценивание параметров модели в соответствии с п. 4.2.; нахождение прогноза и его точности с учетом нелинейного тренда и преобразований, обратных нормализующим. В Приложении 2 приведен пример построения кинематической модели процесса осадки и прогнозирования по ней.
4.5. Динамические стохастические модели объединяют свойства ряда методов математического описания процессов деформации точек земной поверхности и гидротехнических сооружений и содержат три основные составляющие, из которых складывается развитие во времени наблюдаемого перемещения.
Первая составляющая отражает динамические свойства системы сооружение - среда 40, т.е. представляет долю перемещения, происходящего по инерции в результате возникшего ранее движения сооружения. Вторая составляющая динамической модели характеризует долю перемещения, возникающего под влиянием основных входных воздействий. Третья составляющая включает в себя долю перемещения, происходящего в результате действия всех не учтенных двумя первыми составляющими модели факторов. При этом процесс влияния неучтенных факторов, называемый шумовой компонентой, рассматривается как еще одно входное воздействие, выявленные закономерности развития которого описываются моделью в виде авторегрессии, дополняющей каждую динамическую модель.
4.6. Динамические модели представляются типами «вход - выход» 41 или в пространстве состояний 42 с операторами связи в виде дифференциальных или рекуррентных 43 уравнений, которые являются соответственно непрерывной и дискретной формами описания процессов. Кроме того, для описания линейных динамических систем могут использоваться эквивалентные вышеуказанным операторы связи в виде переходных характеристик 44. Между дискретной и непрерывной формами описания должна обеспечиваться связь путем совпадения переходных характеристик в узлах дискретизации процесса.
4.7. Наблюдаемые процессы деформации, в силу непрерывности и монотонности их развития, описываются с достаточной точностью Дифференциальными (рекуррентными) уравнениями первого и второго порядков, называемыми соответственно инерционными звеньями первого и второго порядков. Звено первого порядка учитывает инерционное запаздывание реакции сооружения на гармоническое входное воздействие продолжительностью до одной четверти гармоники, а звено второго порядка- до половины гармоники. Таким образом, для сезонных гармонических изменений температуры воздуха и гидростатического давления, являющихся основными входными воздействиями при описании годичных изменений перемещений, звено первого порядка учитывает инерционное запаздывание продолжительностью до 3 мес. звено второго порядка - продолжительностью до 6 мес.
4.8. Для прогнозирования процессов деформации земной поверхности и гидротехнических сооружений в разработанном программном комплексе предусмотрено использование трех модификаций динамических моделей. Эти модификации представлены комплексной динамической моделью, двузвеньевой моделью и нелинейной динамической моделью. Принципы построения комплексной динамической модели рассмотрены в пп. 4.9 - 4.13., двузвеньевой и нелинейной моделей - в пп. 4.14 - 4.17.
4.9. Прогнозирование процессов деформации земной поверхности и гидротехнических сооружений при эксплуатации водохранилищ в большинстве случаев обеспечивается с необходимой точностью применением линейных стационарных 45 динамических моделей, являющихся вариантами комплексной динамической модели. Так, например, модель типа «вход - выход» со структурой в виде инерционного звена второго порядка, описывающая процесс перемещения одной наблюдаемой точки под воздействием двух основных факторов, имеет следующее рекуррентное выражение:
x k = φ 1 x k -1 + φ 2 x k -2 + β1 u 1, k + β2 u 2, k + γω k , (1)
где x k - выходная переменная, т.е. значение перемещения на k -м шаге дискретизации; u 1, k , u 2, k - вход, выраженный значениями двух воздействующих факторов; ω k - шумовая компонента; φ1, φ2 - коэффициенты динамики, отражающие соответственно степень влияния на x k значений x k -1 , x k -2 , β1, β2, γ - коэффициенты, характеризующие соответственно степень влияния на x k значений u 1, k , u 2, k ω k .
В модели (1) путем предварительного центрирования процесса может выделяться постоянная составляющая x 0 , отражающая среднее влияние входных воздействий на величину перемещения в интервале периода основания прогноза; реализация такого приема показана в Приложении 3. Выделение x 0 улучшает обусловленность систем нормальных уравнений, решаемых для оценивания параметров, и повышает устойчивость 46 модели.
4.10. Модель шумовой компоненты, дополняющая динамическую модель (1), выражается авторегрессионными зависимостями первого порядка ( API ) или второго порядка (АР2), которые имеют соответственно следующий вид:
AP 1
![]() (2)
(2)
AP 2
![]() (3)
(3)
где ρ, μ, η, - коэффициенты соответствующих авторегрессий; ξ k - некоррелированный процесс, называемый белым шумом.
Выбор AP 1 или АР2 выполняется в зависимости от характера изменения остаточных погрешностей построения модели (1) и показан в Приложении 3.
4.11. Матричное выражение модели (1), используемой, например, совместно с моделью (2), будет представлять, по существу, рассматриваемые модели в пространстве состояний. При этом вектор состояний оказывается расширенным за счет включения модели шумовой компоненты. Динамическая модель, выраженная в пространстве состояний, имеет следующий общий вид:
X k = Ф X k-1 + BU k + Гξk, (4)
где X k = [ x 1, k , x 2 , k , ω k ] T - вектор состояний, x i , k = x ( k - i +1) , i = 1,2,3;
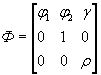 ;
;
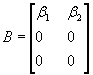 ;
; 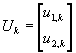 ;
; 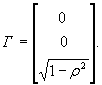 (5)
(5)
4.12. При построении модели (4), описывающей процесс в виде одной реализации, т.е. со структурой (1), нахождение статистических оценок производится путем осреднения значений реализации по времени. Определение параметров модели в этом случае осуществляется по вычисленному одношаговому прогнозу
![]() остаточным
погрешностям
остаточным
погрешностям ![]() и корреляционной
функции
и корреляционной
функции
![]() (6)
(6)
где N - число шагов дискретизации на периоде основания прогноза; (m = 0, 1, 2...) m < N - временной сдвиг.
Вначале оцениваются параметры φ1, φ2, β 1 , β2 путем минимизации функционала 47
![]() (7)
(7)
Для оценивания параметров γ, ρ минимизируется функционал
![]() (8)
(8)
где ![]() - коэффициенты корреляции, полученные
по аппроксимирующему уравнению.
- коэффициенты корреляции, полученные
по аппроксимирующему уравнению.
В случаях построения динамической модели для процесса, образованного семейством реализаций, значения оценок математического ожидания и корреляционной функции находятся по формулам
![]() (9)
(9)
![]() (10)
(10)
где L - число
реализаций; j - номер реализации; ![]()
При этом оценивание параметров модели со структурой (1) должно производиться в следующем порядке. Вначале, находятся параметры φ1, φ 2 путем минимизации функционала
![]() (11)
(11)
где через nm обозначены изменяющиеся моменты времени. Затем определяются параметры β1, β2 путем минимизации функционала
![]() (12)
(12)
Таким образом, в случае построения модели, описывающей процесс перемещения одного деформационного знака, следует прежде всего оценивать совместно параметры φ и β по математическому ожиданию (7). При построении модели, описывающей статистически однородный процесс перемещения семейства деформационных знаков, необходимо вначале оценивать параметр φ по корреляционной функции (11), а затем параметр β - по математическому ожиданию (12). Параметр у во всех моделях оценивается последним по корреляционной функции (8), одновременно с ним оцениваются по такой же корреляционной функции параметры моделей AP 1 или АР2. Указанный порядок построения моделей повышает в соответствии с их структурой точность математического описания и прогнозирования.
4.13. Прогнозы перемещения и их точность определяются по рекуррентной прогнозной модели последовательно шаг за шагом, начиная с последних на периоде основания прогноза значений перемещения и остаточных погрешностей. Так, например, для (4) прогнозы находятся по формуле
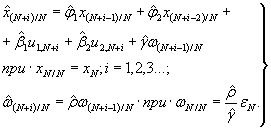 (13)
(13)
Точность прогнозов, выраженная через дисперсию D , предвычисляется по формуле
![]() (14)
(14)
где
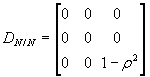
В Приложении 3 приведен пример, отражающий методы оценивания параметров комплексной динамической модели и прогнозирования по ней.
4.14. Двузвеньевая модель представляет собой последовательное соединение двух инерционных звеньев первого порядка. Такая структура модели позволяет учитывать инерционное запаздывание продолжительностью до половины основной гармоники, сохраняя при этом хорошие сглаживающие свойства математического описания, присущие звену первого порядка, и высокую точность описания, присущую звену второго порядка. Двузвеньевая модель во многих случаях декоррелирует входные воздействия и обладает устойчивостью.
4.15. Двузвеньевая стационарная модель непрерывного процесса одномерного перемещения x ( t ), включающая n входных воздействий, представленная типом «вход - выход», имеет вид
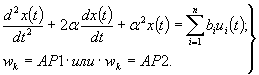 (15)
(15)
Модель (15) строится с помощью разработанного программного обеспечения. Описание процесса в непрерывном времени по данным дискретных наблюдений достигается при условии совпадения в узлах дискретизации переходных функций непрерывной и дискретной моделей. За счет выполнения этого условия обеспечивается также совместное использование непрерывной модели процесса перемещения x ( t ) с дискретной моделью процесса шумовой компоненты w k .
4.16. Нелинейная динамическая модель служит для описания и прогнозирования процессов деформации, протекающих при изменяющихся динамических свойствах системы сооружение - среда. В этой модели коэффициент динамики является переменным и поэтому обозначается через φ k . Поскольку параметр φ k не наблюдается, его приходится определять с помощью дополнительной динамической модели на каждом шаге дискретизации, начиная с первого, где φ k = φ0 находится как для линейной модели. В случае описания одномерного процесса, развивающегося под влиянием n динамических воздействий, нелинейная модель, представленная типом «вход - выход», имеет вид
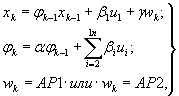 (16)
(16)
где обозначения соответствуют принятым выше для динамических моделей, коэффициент α характеризует динамику изменения параметра φ k .
4.17. Для определения параметров двузвеньевой и нелинейной моделей на периоде основания прогноза аппроксимируется условное математическое ожидание
![]() (17)
(17)
с применением последовательного симплекс-метода (ПСМ) 48 путем минимизации функционалов:
для двузвеньевой модели
![]() (18)
(18)
для нелинейной модели
![]() (19)
(19)
где α, β i , b i , φ 0 , γ - оцениваемые параметры моделей; N - количество сечений, попадающих на период основания прогноза.
При минимизации функционала (18) используются численные методы нахождения интегралов. Параметр γ и параметры моделей шума AP 1 или АР2 оцениваются в порядке, указанном в п. 4.12. Прогнозы и их точность по двузвеньевой, и нелинейной динамическим моделям определяются на ЭВМ с помощью разработанного комплекса программ.
4.18. Помимо описанных выше динамических моделей, построение которых выполняется с помощью разработанного комплекса программ, для прогнозирования процесса перемещения могут использоваться и другие виды динамических моделей. Так, например, в ряде случаев целесообразно строить модель, состоящую из системы комплексных моделей, предназначенных для решения общей сложной прогнозной задачи. Такой задачей является декорреляция основных входных воздействий, поскольку взаимозависимость входных воздействий приводит, как правило, к неустойчивости модели, если в ней учитываются совместно эти воздействия.
Хорошо зарекомендовала себя динамическая модель, декоррелирующая два входных воздействия, состоящая из следующей системы уравнений:
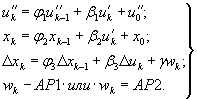
В модели (20) входными воздействиями u k ' и u k ", вызывающими перемещение x k , служат соответственно температура воздуха и гидростатическое давление, которое на многих эксплуатируемых ГЭС имеет высокую степень взаимной корреляционной зависимости. В таком случае два первых уравнения модели выражают зависимость гидростатического давления и перемещения от температуры воздуха. Третье уравнение описывает зависимость D x k от D u k , где D x k - вычисленные на периоде основания прогноза разности фактических и найденных по второму уравнению значений D x k , D u k - соответствующие разности между фактическими и найденными по первому уравнению значениями u k ". Модель (20), построенная с введением транспортного запаздывания, позволяет эффективно выполнять краткосрочные прогнозы. На ее основе разработана табличная форма прогнозирования, показанная в Приложении 4.
5. МЕТОДОЛОГИЧЕСКИЕ ПРИНЦИПЫ ПРОГНОЗИРОВАНИЯ
В Руководстве не представляется возможным рекомендовать общую методику прогнозирования, опирающуюся на единые требования к исходной информации, поскольку пока отсутствуют упорядоченные программы и схемы геодезических наблюдений за сооружениями ГЭС различных типов и приходится использовать исходную информацию в разнообразном имеющемся виде. В связи с этим даются методологические принципы, позволяющие определиться с методикой прогнозирования в зависимости от конкретных условий функционирования сооружений ГЭС и организации на них геодезических и других натурных наблюдений. Используя эти принципы, следует учитывать общие положения, изложенные в разделе 2, виды моделей и методы их построения, показанные в разделе 4, а также наличие разработанного программного обеспечения.
5.1. Согласно понятию прогностики содержание прогнозирования заключается в процессе разработки прогнозов. Разработку прогнозов следует начать с анализа исходных данных и выбора вида моделей в зависимости от полноты и формы имеющейся исходной информации. Во всех возможных случаях предпочтение следует отдавать динамическим моделям, так как свойственный гидротехническим сооружениям сезонный характер изменения перемещений существенно ограничивает возможности применения кинематических моделей, снижая точность прогнозирования по ним. Опыт показывает, что для эксплуатируемых в нормальных условиях плотин ГЭС пригодны комплексные стационарные динамические модели и двузвеньевая модель, которые обеспечивают высокую точность краткосрочных прогнозов различных наблюдаемых перемещений. Необхо димость использования нелинейной модели типа (16) возникает в случаях прогнозирования процессов, развивающихся в условиях быстроменяющихся свойств сооружения и величин перемещений, и когда требуется адаптация модели.
Анализ исходных данных заключается в изучении результатов натурных наблюдений за поведением несущих конструкций, за изменением воздействующих факторов, в увязывании этих результатов с конкретными инженерно-геологическими, конструктивными, строительно-эксплуатационными и другими условиями работы исследуемого сооружения. На основании совместного изучения графиков изменения наблюдаемых перемещений и воздействующих факторов, а также всех других данных о прогнозном фоне:
1) выбираются с учетом пп. 2.3, 2.4 периоды основания прогноза и периоды упреждения прогноза;
2) намечаются в соответствии с принципом конструктивного применения вероятностно-статистического аппарата 49 статистически однородные семейства перемещений и циклы наблюдений, необходимые для предварительного построения моделей с контрольным прогнозированием и для их окончательного построения;
3) определяется структура моделей (выбор входных воздействий и выходных переменных, порядок инерционных звеньев и величина транспортного запаздывания);
4) производится подготовка исходных данных для введения в ЭВМ.
Дальнейшие этапы разработки прогнозов заключаются в анализе полученных с ЭВМ результатов контрольного прогнозирования согласно принципу - верификации, указанному в п. 2.5, в построении окончательных моделей на полном периоде основания прогноза и их производственном использовании, если верификация подтвердила хорошее качество моделей. В случаях неудовлетворительного качества моделей повторяются все предыдущие этапы их разработки для того, чтобы найти вид и структуру моделей, адекватно описывающих исследуемые процессы.
5.2. Статистическая однородность реализаций процесса характеризуется примерно одинаковой интенсивностью изменения во времени изучаемого перемещения по заложенным в конструкции различным деформационным знакам, которые имеют общие условия работы. Статистическая неоднородность проявляется в существенно различном характере развития процесса по отдельным реализациям, а чаще - в разделении реализаций процесса на отдельные статистически однородные семейства. Если такое разделение вызвано лишь различием значений величины перемещения при одинаковой интенсивности их развития, то можно восстановить статистическую однородность путем перехода от значений перемещения к их при ращениям; если же семейства реализаций имеют различную интенсивность и форму развития, то, исходя из конструктивного применения вероятностно-статистических методов, необходимо строить модели для отдельных семейств реализаций даже при их малом количестве.
В разработанном программном обеспечении отбор статистически однородных семейств реализаций формализован и автоматизирован. Формализация отбора основывается на том, что геодезические данные о перемещении деформирующихся конструкций наиболее объективно отражают фактическую однородность комплекса условий работы сооружения. Одновременно с отбором статистически однородных семейств реализаций процесса в программном обеспечении предусмотрена проверка сформированных семейств на нормальность распределения, а в необходимых случаях - нормализация процесса. Таким образом, автоматически осуществляется проверка и подготовка исходной геодезической информации к моделированию при условии выполнения заданных предпосылок для обоснованного конструктивного применения вероятностно-статистических методов.
Продолжительность периодов основания прогноза и упреждения определяется их взаимной согласованностью, назначением и срочностью прогнозирования. Она зависнет также от неизменности прогнозного фона, не учитываемого трендом, для кинематических моделей и от неизменности общего состояния сооружения для динамических моделей. Увеличение продолжительности периода упреждения может быть достигнуто путем применения адаптирующейся нелинейной динамической модели типа (16). Кроме того, при описании гармонических процессов период основания прогноза должен охватывать не менее одного полного цикла сезонных изменений моделируемого процесса.
Число циклов наблюдений, необходимое для построения динамических моделей, зависит от того, какую динамику изменения перемещений должны описывать модели - сезонную или суточную. В случаях, когда моделируются процессы сезонных перемещений, характеризующих поведение сооружения в целом, достаточно иметь на годичном интервале 12 циклов наблюдении. Даже этот объем наблюдений можно при необходимости сократить так, чтобы охватывались лишь периоды возникновения экстремальных сезонных перемещений. Если же требуется моделировать процессы суточных изменений перемещений, характеризующие поверхностные деформации, то необходимо иметь не меньше 3 циклов наблюдений в сутки, соответствующих основной гармонике суточного изменения температуры воздуха. Продолжительность циклов наблюдений должна согласовываться со скоростью развития деформации.
В кинематических и динамических моделях количество циклов наблюдений на периоде основания прогноза должно также обеспечивать минимальное число степеней свободы для оценивания параметров моделей, а величина межциклового периода должна сохранять взаимосвязь между соседними значениями наблюдаемого перемещения. В таблице приведено наименьшее число наблюдений, необходимое для оценивания различного числа параметров моделей, рассмотренных в разделе 4. При этом в число оцениваемых параметров не входят параметры модели шумовой компоненты, оцениваемые по остаточным ошибкам построения динамической модели.
|
Вид модели |
Количество входных воздействий |
Число оцениваемых параметров |
Необходимое число циклов |
|
Кинематическая модель |
- |
5...9 |
6...10 |
|
|
Комплексная модель на базе рекуррентного уравнения |
|
|
|
|
|
|
|
|
|
|
|
1-го порядка |
1 |
2 |
3 |
|
|
2 |
3 |
4 |
|
|
|
3 |
4 |
5 |
|
|
|
4 |
5 |
6 |
|
|
|
5 |
6 |
7 |
|
|
|
2-го порядка |
1 |
3 |
4 |
|
|
2 |
4 |
5 |
|
|
|
3 |
5 |
6 |
|
|
|
4 |
6 |
7 |
|
|
|
5 |
7 |
8 |
|
|
Двузвеньевая модель |
1 |
2 |
3 |
|
|
2 |
3 |
4 |
|
|
|
3 |
4 |
5 |
|
|
|
4 |
5 |
6 |
|
|
|
5 |
6 |
7 |
|
|
|
Нелинейная модель с переменным коэффициентом динамики |
1 |
3 |
4 |
|
|
2 |
4 |
5 |
|
|
|
3 |
5 |
6 |
||
|
4 |
6 |
7 |
|
|
|
5 |
7 |
8 |
|
5.3. Выбор структуры кинематических моделей сводится в основном к выявлению вида нелинейного тренда или к кусочной линеаризации процесса, отражающей принцип непрерывности прогнозирования, рассмотренный в п. 2.3. В программном обеспечении кинематической модели предусмотрена аппроксимация и выделение трендов в виде экспоненты и синусоиды.
Важнейшим этапом определения структуры динамических моделей является выбор входа и выхода. Вид выходной переменной определяется наличием геодезических данных о перемещении конкретных несущих конструкций сооружения и представляется, как правило, результатами геодезических наблюдений за процессом деформации сооружения. За выходную переменную модели, строящейся на основе геодезических данных, может быть также взят и другой наблюдаемый процесс, связан ный функционально с использованными в модели геодезическими данными и характеризующий напряженно-деформированное состояние конструкций. Выбор входных воздействий производится на основании анализа теоретических предпосылок, особенностей конструкций и условий работы сооружений, накопленного опыта моделирования, а также исходя из сравнения графиков изменения предполагаемых входа и выхода.
В период эксплуатации гидротехнических сооружений за основные входные воздействия в большинстве случаев принимаются температура воздуха и гидростатическое давление, поскольку они прямо или косвенно представляют большинство воздействий, вызывающих перемещения при сложившихся начальных условиях. Если прогнозирование осуществляется на периоде строительства, то к отмеченным основным входным воздействиям добавляются рост нагрузки в процессе возведения сооружения и монтажа оборудования, изменение объема водохранилища в ходе его наполнения. В качестве входных воздействий могут использоваться и другие факторы, если в конкретных условиях они оказывают определяющее влияние на величины наблюдаемых перемещений.
Решение вопроса о выборе входных воздействий влияет на дальнейшие этапы разработки структуры динамической модели в части определения порядка инерционного звена и декорреляции входных воздействий. Порядок инерционного звена модели определяется в соответствии с пп. 2.4, 4.7 в зависимости от продолжительности инерционного запаздывания и необходимости включения в модель транспортного запаздывания. Продолжительность инерционного запаздывания определяется путем сопоставления графиков изменения входа и выхода модели, имеющих гармонический характер. Величина фазового сдвига выходной переменной относительно входного воздействия характеризует продолжительность инерционного запаздывания. В. случаях, когда гармонический характер входа и выхода слабо выражен, можно оценить продолжительность инерционного запаздывания по отдельным соответствующим выбросам, имеющим место в развитии входного и выходного процессов. Модель на основе звеньев 2-го порядка следует строить в случаях, когда инерционное запаздывание сезонных процессов превышает 3 месяца и предполагается использовать эти модели для анализа описываемого процесса перемещения. Если модель будет использоваться только для прогнозирования, следует отдавать предпочтение основе в виде инерционного звена 1-го порядка, вводя при необходимости транспортное запаздывание.
Корреляция основных входных воздействий возникает в результате того, что на многих эксплуатируемых ГЭС сезонные изменения температуры воздуха почти функционально связаны с изменениями гидростатического давления, а в период наполнения водохранилища гидростатическое давление зависит от ?. Имеются и другие подобные связи между воздействующими факторами. Одновременный вход коррелирующих входных воздействий в динамическую модель приводит, как правило, к ее неустойчивости. Декорреляция входных воздействий осуществляется преимущественно путем их последовательного ввода, как это сделано в модели (20), или в результате применения двузвеньевой модели (15). В отдельных случаях можно использовать одно из основных взаимозависимых воздействий, если оно не снижает точности прогнозирования и согласуется с целью исследования (см., например, Приложение 3).
5.4. Порядок формирования исходных данных геодезических и других натурных наблюдений для построения моделей на ЭВМ зависит от полноты, содержания и качества этих данных. Отправной позицией при формировании исходных данных являются циклы геодезических наблюдений. Интервал времени между циклами наблюдений может быть в принципе произвольным при условии, что выполненные геодезические наблюдения охватывают основные закономерности развития исследуемого процесса деформации, а результаты наблюдений за воздействующими факторами соответствуют циклам геодезических наблюдений. Произвольная циклограмма наблюдений полностью реализована в программном обеспечении кинематической модели. Однако для динамических моделей такой подход значительно увеличивает объем математической обработки, выполняемой при построении моделей. По этой причине желательно организовывать геодезические наблюдения с равными межцикловыми периодами, на которые рассчитано программное обеспечение. В случаях, когда межцикловые периоды оказываются неодинаковыми, необходимо интерполировать значения перемещения между непосредственными наблюдениями так, чтобы оцениваемый динамической моделью случайный процесс имел сечение через равные интервалы времени. Опыт подтверждает правильность такого методического приема, если непосредственные наблюдения охватывают характерные моменты развития процесса.
Развитие процессов основных воздействующих факторов (температуры воздуха, гидростатического давления и др.) наблюдается, как правило, несколько раз в сутки. При подготовке данных для построения динамических моделей необходимо сглаживать результаты наблюдений за воздействующими факторами путем осреднения их значений на интервалах между циклами геодезических наблюдений.
Для гармонических процессов перемещений, таких, как горизонтальные перемещения плотины, наблюдаемые по прямым и обратным отвесам, применяются два способа формирования исходных геодезических данных. По первому способу исходные геодезические данные используются в обычной последовательности их получения за ряд лет, попадающих на период основания прогноза. Однако модели процесса, построенные «а длинном интервале времени, охватывающем ряд основных гармоник, нередко оказываются неустойчивыми. Второй способ, повышающий устойчивость моделей гармонических процессов, заключается в том, что интервал периода основания прогноза ограничивается одним календарным годом, т.е. одной основной гармоникой, в пределах которой результаты наблюдений разных лет рассматриваются как отдельные реализации процесса. При этом в динамическую модель каждая реализация вводится со своими значениями входных воздействий. Таким способом строится, например, модель (20). В результате прогнозирования по построенной таким образом модели вводятся поправки за удаленность начала года, на который ищется прогноз, от конца периода основания прогноза. Поправки рассчитываются по специальной регрессионной или динамической модели.
В отдельных случаях возникает необходимость строить динамические модели по неполному объему геодезических данных при достаточной информации о воздействующих факторах. Имеется опыт успешного решения таких задач путем восстановления ненаблюдаемых сечений процесса или путем моделирования по сезонным огибающим. Восстановление сечений можно выполнять, если на концах интервала времени с упущенными наблюдениями измерены значения перемещения и в этом интервале; имеются наблюдения другого аналогичного процесса перемещения. Тогда, исходя из предположения о пропорциональности развития обоих процессов, вычисляется по концам интервала средний коэффициент пропорциональности между величинами перемещений двух процессов. С помощью этого коэффициента восстанавливаются ненаблюдавшиеся значения перемещения одного процесса по соответствующим наблюдавшимся значениям другого процесса перемещения. Построение моделей по сезонным огибающим выполняется на том основании, что только зимние или только летние результаты наблюдений отражают динамические и другие свойства процесса, присущие данному сезону, даже при недостаточном числе циклов наблюдений в целом на годичном интервале.
Приложение 1
ПОЯСНЕНИЕ ИСПОЛЬЗУЕМЫХ ТЕРМИНОВ 1
1 Термины прогностики даются в соответствии с работой Терминология: Прогностика/ АН СССР. - М.: Наука, 1978. – Вып. 92 :
|
№ п. п |
Термин |
Определение или упрощенное описание |
|
1 |
Объект прогнозирования |
В качестве объектов прогнозирования могут выступать процессы, явления, события, на которые направлена познавательная и практическая деятельность человека с целью получения научно обоснованных оценок состояния объекта в будущем |
|
2 |
Прогнозная экстраполяция |
Метод прогнозирования, основанный на математической экстраполяции, при котором выбор аппроксимирующей функции осуществляется с учетом условий и ограничений развития объекта прогнозирования |
|
3 |
Эндогенная переменная |
Количественная характеристика объекта прогнозирования, являющаяся изменяемой, принимаемая для описания объекта и отражающая его собственные свойства |
|
4 |
Динамический ряд |
Временная последовательность наблюдавшихся значений переменной объекта прогнозирования |
|
5 |
Выходная переменная динамической модели процесса деформации сооружения |
Количественная характеристика собственных свойств объекта прогнозирования в виде наблюдаемого процесса перемещения или зависящего от него другого наблюдаемого процесса, возникающего под влиянием входных воздействий (см. 10); между входными воздействиями и выходной переменной в динамической модели устанавливается, оператор связи. Можно называть просто «выход» |
|
6 |
Экзогенная переменная |
Количественная характеристика объекта прогнозирования, принимаемая для его описания, связанная со свойствами прогнозного фона, служащая в модели аргументом |
|
7 |
Прогнозный фон |
Совокупность внешних по отношению к объекту прогнозирования условий, существенных для решения задачи прогноза |
|
8 |
Период основания прогноза |
Промежуток времени, на базе которого строятся математическая модель. |
Продолжение таблицы
|
№ п.п. |
Термин |
Определение или упрощенное описание |
|
9 |
Период упреждения |
Промежуток времени, на который разрабатывается прогноз |
|
10 |
Входные воздействия динамической модели процесса |
Количественные характеристики основных факторов силового и несилового характера, вызывающих механическое движение сооружения в целом и его частей. Можно называть просто «вход» |
|
11 |
Принцип непрерывности прогнозирования |
Принцип прогнозирования, требующий корректировки прогнозов по мере поступления новых данных об объекте прогнозирования |
|
12 |
Дисконтирование информации об объекте прогнозирования |
Уменьшение информативности значений переменной объекта прогнозирования по мере удаления моментов их измерений в прошлое |
|
13 |
Ошибка прогноза |
Апостериорная величина отклонения прогноза от действительного состояния объекта |
|
14 |
Контрольный период |
Период упреждения прогноза, на котором измерены действительные значения процесса перемещения; создается для контроля первичного построения модели за счет невключения последних циклов наблюдений в период основания прогноза |
|
15 |
Поисковый прогноз |
Прогноз, содержанием которого является определение возможных состояний объекта прогнозирования в будущем |
|
16 |
Нормативный прогноз |
Прогноз, содержанием которого является определение путей и сроков достижения возможных состояний объекта прогнозирования в будущем, принимаемых в качестве цели |
|
17 |
Интервальный прогноз |
Прогноз, результат которого представлен в виде доверительного интервала характеристики объекта прогнозирования для заданной вероятности осуществления прогноза |
|
18 |
Точечный прогноз |
Прогноз, результат которого представлен в виде единственного значения характеристики объекта прогнозирования без указания доверительного интервала |
|
19 |
Оперативный прогноз |
Прогноз с периодом упреждения до 1 месяца |
|
20 |
Краткосрочный прогноз |
Прогноз с периодом упреждения от 1 месяца до 1 года |
|
21 |
Среднесрочный прогноз |
Прогноз, с периодом упреждения от 1 года до 5 лет |
|
22 |
Долгосрочный прогноз |
Прогноз с периодом упреждения от 5 до 15 лет |
|
23 |
Дальнесрочный прогноз |
Прогноз с периодом упреждения свыше 15 лет |
|
24 |
Моделирование |
Метод исследования процессов и явлений путем построения их моделей и экспериментирования на моделях. В содержание математического моделирования входит прогнозирование, в том числе по результатам «игры с моделью» |
Продолжение таблицы
|
№ п.п |
Термин |
Определение или упрощенное описание |
|
25 |
Прогнозная модель |
Модель объекта прогнозирования, исследование которой позволяет получить информацию о возможных состояниях объекта в будущем или путях и сроках их осуществления. По математической модели объекта не всегда можно получить непосредственно информацию в нужной форме, поэтому требуется переход к прогнозной модели. Например, от эмпирического закона распределения случайного процесса приходится переходить к его характеристикам в виде условных моментных функций (см. 26) |
|
26 |
Две первые условные моментные функции случайного процесса |
Условное математическое ожидание и условная корреляционная функция случайного процесса, используемые в виде прогнозной модели, позволяющие находить оптимальные прогнозы конкретных реализаций процесса и предвычислять точность прогнозов (см. 27). В динамической модели условные моментные функции определяются по ее решению |
|
27 |
Точность прогноза |
Оценка доверительного интервала прогноза для заданной вероятности его осуществления |
|
28 |
Инерционное запаздывание |
Запаздывание реакции сооружения на входные воздействия. Учитывается динамической моделью |
|
29 |
Транспортное запаздывание |
Здесь понимается как постоянный интервал времени, вводимый в динамическую модель за счет части инерционного запаздывания. Для этого при подготовке исходных данных к построению модели приводятся в соответствие значения входных воздействий и выходной переменной, удаленные друг от друга по времени на величину выбранного интервала транспортного запаздывания |
|
30 |
Тренд |
Аналитическое представление изменения, переменной во времени (а в динамической модели - и под влиянием входных воздействий), полученное в результате выделения детерминированной составляющей процесса из динамического ряда |
|
31 |
Верификация прогноза |
Оценка достоверности и точности или обоснованности прогноза |
|
32 |
Достоверность прогноза |
Оценка вероятности осуществления прогноза для заданного доверительного интервала |
|
33 |
Коридор погрешностей |
Изменение во времени предвычисленной по модели точности прогнозирования в виде одинарного или удвоенного среднего квадратического отклонения |
|
34 |
Нормальный процесс |
Случайный процесс, подчиняющийся нормальному закону распределения |
Продолжение таблицы
|
№ п.п. |
Термин |
Определение или упрощенное описание |
|
35 |
Нормализованный процесс |
Случайный процесс, не имеющий нормального распределения, но получивший его, например, после логарифмического или экспоненциального преобразования значений реализаций процесса в каждом сечении |
|
36 |
Инверсная верификация |
Верификация прогноза путем проверки адекватности прогнозной модели на периоде времени, имеющем выполненные наблюдения за объектом |
|
37 |
Линейность |
Понятию линейности можно придавать различное толкование при рассмотрении кинематических и динамических моделей. В кинематических моделях под линейностью обычно понимается линейная функциональная зависимость величины перемещения от времени, т.е. линейность тренда. В динамических моделях линейность означает соблюдение принципов пропорциональности и суперпозиции между входом и выходом, устанавливаемых с помощью линейного оператора, что позволяет описывать тренды нелинейной формы, возникающие под действием входа. Простейшим линейным оператором служит экспонента и с этой точки зрения кинематическая модель с нелинейным трендом в виде экспоненты является линейной в смысле линейного оператора. Кроме того, кинематические модели могут быть нелинейными по параметрам, если их оценки находятся из решения системы линейных уравнений; примером такой модели служит полиномиальная зависимость, а экспоненциальная зависимость является нелинейной по параметрам. |
|
38 |
Нелинейность |
С учетом 38 следует говорить о нелинейности динамических моделей, которая означает, что связь между входом и выходом нельзя представить при помощи одной прямой линии. При этом приращение выхода зависит не только от приращения входа, но и от других условий, таких, как начальный уровень входа или величина его приращения, нарушения в структуре системы сооружение - среда (см. 40) и т. п. |
|
39 |
Центрированный процесс |
Центрированным
случайным процессом |
Продолжение таблицы
|
№ п.п. |
Термин |
Определение или упрощенное описание |
|
40 |
Система сооружение - среда |
Состоит из трех основных подсистем: сооружения, грунтового основания, внешней среды в результате взаимодействия которых возникает процесс деформации сооружения. Динамическая модель процесса деформации является также системой, представляющей в упрощенной открытой форме результаты взаимодействия подсистем в системе сооружение - среда |
|
41 |
Динамическая модель типа «вход - выход» |
Дифференциальное или рекуррентное уравнение, определяющее соотношение между изменениями входных и выходных физических величин. Например, стационарная (см. 45) детерминированная модель линейной системы, связывающая вход u ( t ) с выходом x ( t ), задается дифференциальным уравнением n -го порядка где α i - коэффициенты, отражающие динамические свойства системы; b j - коэффициенты, характеризующие степень влияния входных воздействий |
|
42 |
Представление динамической модели в пространстве состояний |
Переход от модели типа «вход - выход» (см. 41) к модели в пространстве состояний выполняется путем преобразования дифференциального уравнения n -го порядка в систему дифференциальных уравнений 1-го порядка, выраженную в матричной форме. Система из n уравнений 1-го порядка определяется полностью, когда заданы все коэффициенты и известны n начальных условий. Начальные условия образуют n -мерный вектор, называемый вектором состояний системы в начальный момент t 0 - Дальнейшее изменение состояний системы задается значениями входа в произвольный момент t . В моделях процессов деформации сооружений переменными состояния являются наблюдаемые геодезическими методами перемещения и их производные |
|
43 |
Рекуррентное выражение |
Формула, выражающая любой член последовательности от некоторого начального члена через предшествующие члены |
|
44 |
Переходные характеристики динамической системы |
Показывают, как выход системы изменяется во времени под действием входа. В линейных системах используются характеристики в виде переходной функции, передаточной функции и частотной характеристики. Реакция системы на импульсное воздействие является импульсной переходной функцией |
Продолжение таблицы
|
№ п.п. |
Термин |
Определение или упрощенное описание |
|
|
|
Оператор, преобразующий воздействие на входе в реакцию системы на выходе, представляет передаточную функцию. Частотная характеристика отражает относительную реакцию системы на гармонические воздействия |
|
45 |
Стационарная модель |
Динамическая модель, имеющая постоянные параметры на исследуемом интервале времени |
|
46 |
Устойчивая модель |
Модель, у которой постепенно стабилизируется коридор погрешностей. Например, модель в виде инерционного звена 1-го порядка теряет устойчивость, когда коэффициент динамики φ > 1; в общем случае условием устойчивости системы является отрицательность действительной части всех корней характеристического уравнения |
|
47 |
Функционал |
Закон, по которому каждой функции из определенного класса числовых функций соответствует значение некоторого числового параметра. Понятие функционала совпадает с понятием функции, если класс функций состоит из констант, т. е. закон приводит в соответствие числа, выражающие значения аргумента и функции. В результате минимизации функционала находятся оптимальные оценки параметров модели при заданном условии |
|
48 |
Последовательный симплексный метод (ПСМ) |
Используется в данной работе для оценивания параметров моделей в случаях, когда минимизируемые функционалы оказываются сложными, имеют нелинейный, случайный характер. Сущность ПСМ. заключается в формировании в пространстве оцениваемых параметров многогранника, в вершинах которого вычисляются значения функционала. Уточнение значений функционала производится путем «отражения» наихудшей вершины многогранника относительно противоположной грани. Полученная совокупность вершин рассматривается как исходная для следующего шага оптимизации |
|
49 |
Конструктивное применение вероятностно- статистического аппарата |
Процесс деформации любого сооружения имеет преобладающую детерминированную основу, обусловленную упорядоченной структурой системы сооружение - среда и жесткими связями в ней. Это позволяет конструктивно использовать вероятностно-статистические аппарат для описания процессов деформаций т.е. не соблюдать критериев в отношении объема выборок при обязательном обеспечении статистической однородности моделируемых процессов, при правильности размещения деформационных знаков и назначений циклов наблюдений |
Приложение 2
ПРИМЕР ПОСТРОЕНИЯ КИНЕМАТИЧЕСКОЙ МОДЕЛИ
ПРОЦЕССА ОСАДКИ НА НИЖНЕКАМСКОЙ ГЭС
И ВЫПОЛНЕНИЯ ПРОГНОЗИРОВАНИЯ
Кинематическая модель строилась по результатам наблюдений за процессом вертикального перемещения шести поверхностных осадочных марок, заложенных в здание ГЭС, образующих семейство реализаций, которое можно принять за статистически однородное (рисунок). В связи с тем, что рассматриваемый
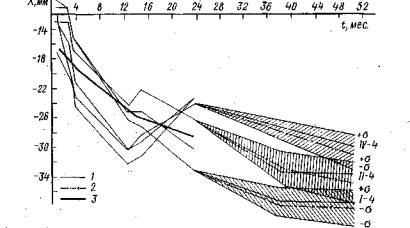
Прогнозирование процесса осадки Нижнекамской ГЭС по кинематической модели.
процесс вертикального перемещения имеет сезонные колебания, его описание в целом было бы целесообразно выполнять с помощью динамической модели. Для построения кинематической модели процесса осадки можно взять только результаты наблюдений, полученные в холодное время года, когда осадочные марки занимают самое низкое положение. Такой прием называется построением модели по сезонной огибающей наблюдаемого процесса.
Период основания прогноза охватывает 24 месяца - с января 1979 г. по декабрь 1980 г. - и включает в себя 6 используемых циклов, наблюдений, называемых в дальнейшем сечениями процесса. Конец периода контрольного прогнозирования приходится на март 1983 г., его продолжительность составляет 27 месяцев, т.е. весь исследуемый промежуток времени равен 51 месяцу. Прогнозный фон для обоих периодов можно считать
примерно одинаковым: до 1979 г. завершился основной рост нагрузки от строительных и монтажных работ, в 1979 г. осуществлена первая очередь наполнения водохранилища, в последующие 17 месяцев ведется вторая очередь наполнения водохранилища до проектной отметки.
В таблице приведены исходные данные, используемые для построения модели, а также следующие статистические параметры процесса по каждому сечению:
![]()
![]() - отношения асимметрии и эксцесса к своим средним
квадратическим отклонениям;
- отношения асимметрии и эксцесса к своим средним
квадратическим отклонениям; ![]() - оценка
математического ожидания процесса
- оценка
математического ожидания процесса ![]() ;
; ![]() - оценка
среднего квадратического отклонения;
- оценка
среднего квадратического отклонения; ![]() - экспоненциальный
тренд;
- экспоненциальный
тренд; ![]() - оценка математического ожидания
центрированного процесса.
- оценка математического ожидания
центрированного процесса.
Из таблицы видно, что значения процесса вертикального перемещения недостаточно четко выражают на периоде основания прогноза общую тенденцию развития осадки; в перемещении отдельных марок имеют место проявления динамического характера, затрудняющие точное описание процесса с помощью кинематической модели. В общем. характере развития осадки просматривается экспоненциальная форма тренда, аппроксимация которого дала следующее выражение:
![]() (1)
(1)
После
исключения тренда из приведенных в таблице результатов наблюдений образовался
центрированный процесс x ( t ),
для которого
были вычислены оценки математического ожидания ![]() , среднего
квадратического отклонения
, среднего
квадратического отклонения ![]() и нормированной корреляционной функции
и нормированной корреляционной функции
![]() Аппроксимация этих оценок, выполненная
на периоде основания прогноза, дала следующие результаты:
Аппроксимация этих оценок, выполненная
на периоде основания прогноза, дала следующие результаты:
![]() (2)
(2)
![]()
![]() (3)
(3)
![]()
![]() (4)
(4)
Невысокая теснота зависимости, полученная при аппроксимации математического ожидания и обусловленная динамическими колебаниями процесса, компенсируется достаточной тес нотой зависимости, полученной при аппроксимации корреляционной функции. Как показывает опыт, в таких случаях корреляционная функция, отражающая структуру развития процесса, нередко обеспечивает удовлетворительную точность прогнозирования.
|
№ марки |
№ сечения |
|||||
|
1 |
2 |
3 |
4 |
5 |
6 |
|
|
Месяц, год |
||||||
|
1.1979 |
3.1979 |
4.1979 |
1.1980 |
3.1980 |
12.1980 |
|
|
t , мес. |
||||||
|
1 |
3 |
4 |
13 |
15 |
24 |
|
|
Осадка, мм |
||||||
|
1-4 |
-10 |
-11 |
-15 |
-26 |
-27 |
-33 |
|
II - l |
-11 |
-11 |
-15 |
-25 |
-25 |
-30 |
|
II -4 |
-13 |
-13 |
-17 |
-24 |
-22 |
-26 |
|
III -4 |
-13 |
-16 |
- 21 |
-30 |
-29 |
-23 |
|
IV -1 |
-12 |
-19 |
- 24 |
-32 |
-31 |
-23 |
|
IV -4 |
-17 |
-20 |
-23 |
-30 |
-28 |
-24 |
|
Статистические параметры процесса |
Значения параметров |
|||||
|
|
0,74 |
0,16 |
0,06 |
0,04 |
0,35 |
0,56 |
|
|
1,93 |
2,77 |
2,83 |
2,78 |
2,31 |
2,50 |
|
|
-12,67 |
-15.00 |
-19,17 |
-27,83 |
-27,00 |
-26,50 |
|
|
2,899 |
2,422 |
3,950 |
4,021 |
3,251 |
3,162 |
|
|
-16,20 |
-18,16 |
-19,04 |
-24,78 |
-25,64 |
-28,34 |
|
|
3,53 |
3,16 |
-0,13 |
-3,05 |
-1,36 |
1,84 |
Для получения прогноза
центрированного процесса ![]() используется модель (25) Приложения 5,
а характеристика точности прогноза находится по (26) Приложения 5. При этом
значение
используется модель (25) Приложения 5,
а характеристика точности прогноза находится по (26) Приложения 5. При этом
значение ![]() вычисляется по (2) для t 2 , равного времени конца периода упреждения. Аналогично
находится
вычисляется по (2) для t 2 , равного времени конца периода упреждения. Аналогично
находится ![]() по (3), а также
по (3), а также ![]() по (4), где t m = t 1 -
время конца периода основания прогноза, t n
= t 2 . Центрированное значение осадки i -й марки в последнем сечении
периода основания прогноза находится по формуле
по (4), где t m = t 1 -
время конца периода основания прогноза, t n
= t 2 . Центрированное значение осадки i -й марки в последнем сечении
периода основания прогноза находится по формуле ![]() с использованием данных таблицы; из
той же таблицы берется
с использованием данных таблицы; из
той же таблицы берется ![]() . Вышеуказанные
данные позволяют вычислить прогноз
. Вышеуказанные
данные позволяют вычислить прогноз ![]() и его точность
и его точность ![]() . Окончательное
значение прогноза находится с учетом значения тренда, экстраполированного в t 2 :
. Окончательное
значение прогноза находится с учетом значения тренда, экстраполированного в t 2 :
![]() (5)
(5)
Приводим пример расчета контрольных прогнозов по модели (25) Приложения 5, (26) Приложения 5, (5) Приложения 2, подготовка данных для которого выполнена по вышеописанной методике. Прогнозы вычисляются для осадки марки 1-4 на периоды упреждения, равные 15 и 27 месяцам, т. е. Соответственно t 1 = 24 мес., t 2 = 39 мес. и t 1 - 24 мес., t 2 - 51 мес.
В соответствии с (5) Приложения 2 и (25) Приложения 5 имеем
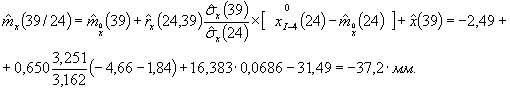
Фактическое значение осадки марки 1-4 в это время достигло 37 мм, т.е. ошибка прогноза ∆ (4) Приложения 5 равна - 0,2 мм.
По (26) Приложения 5 вычисляется точность прогноза:
![]()
Аналогично выполняется прогнозирование в t 2 = 51 сут:
![]()
Ошибка прогноза ∆ (16) Приложения 5 равна - 0,9 мм.
![]() Предвычисленный коридор точности
прогнозирования оказался широким из-за динамических колебаний отдельных марок
на периоде основания прогноза.
Предвычисленный коридор точности
прогнозирования оказался широким из-за динамических колебаний отдельных марок
на периоде основания прогноза.
Результаты контрольного прогнозирования осадки данной марки, а также марок П-4, IV -4 показаны на рисунке.
Приложение 3
ПРИМЕР ПОСТРОЕНИЯ КОМПЛЕКСНОЙ ДИНАМИЧЕСКОЙ МОДЕЛИ ДЛЯ ПРОГНОЗИРОВАНИЯ ПРОЦЕССА
ГОРИЗОНТАЛЬНОГО ПЕРЕМЕЩЕНИЯ ГРЕБНЯ ПЛОТИНЫ КРАСНОЯРСКОЙ ГЭС НА СЕКЦИИ № 22
Пример приводится с целью показа основных этапов технологии оценивания параметров динамической модели и прогнозирования по ней. Для этого взята наиболее простая модель в виде стохастического рекуррентного уравнения 1-го порядка, отражающего зависимость горизонтального перемещения лишь от температуры воздуха; влияние гидростатического давления учитывается косвенно через модель шумовой компоненты, дается подробный алгоритм, промежуточные и конечные результаты вычислений, позволяющие с контролем освоить технологический процесс путем повторения вычислений на ЭМК.
Построение модели ведется на периоде основания прогноза, охватывающем 1976 г., контрольное прогнозирование выполняется на 1977 г. При этом вводится транспортное запаздывание величиной 2 месяца, поскольку в модели используется инерционное звено 1-го порядка, а инерционное запаздывание, выявленное по графикам, достигает 5 месяцев. Исходные данные, используемые для построения модели, а также результаты промежуточных расчетов и контрольного прогнозирования приведены в таблице. Шаг дискретизации модели обозначен через k , равен одному месяцу и соответствует номеру цикла наблюдений. Значения горизонтального перемещения обозначены через x k и даны с точностью отсчитывания по координатометру отвеса. Среднемесячная температура воздуха, действовавшая за 2 месяца до наблюдения соответствующего значения перемещения, обозначена через u k
|
k |
1976 г . |
m |
k ε [m] |
1977 г . |
|||||
|
x k , |
y k , |
ε k , |
uk, ºC |
|
∆ k, |
|
|||
|
1 |
28,35 |
-3,36 |
- |
- |
- |
-10,48 |
27,43 |
-2,17 |
±0,77 |
|
2 |
26,85 |
-15,59 |
-1,15 |
0 |
+ 0,969 |
-8,35 |
26,37 |
-1,47 |
0,88 |
|
3 |
24,15 |
-9,46 |
+1,23 |
1 |
-0,597 |
-21,58 |
24,82 |
+1.41 |
±0,77 |
|
4 |
21,88 |
-19,46 |
+0,14 |
2 |
+0,099 |
-25,28 |
22,36 |
+1,26 |
0,88 |
|
5 |
21,47 |
-13,93 |
-0,43 |
3 |
+0,139 |
-9,43 |
21,18 |
+0,27 |
±0,77 |
|
6 |
21,65 |
-5,80 |
+0,16 |
4 |
-0,087 |
-4,06 |
21,96 |
-0,70 |
0,88 |
|
7 |
22,13 |
+5,59 |
+1,33 |
5 |
-0,285 |
+4,76 |
24,06 |
-0,87 |
±0,77 |
|
8 |
26,27 |
+10,66 |
-1,77 |
6 |
+ 0,312 |
+11,20 |
25,81 |
-1,46 |
0,88 |
|
9 |
27,29 |
+18,13 |
+1,31 |
7 |
-0,273 |
+17,50 |
28,94 |
-0,48 |
±0,77 |
|
10 |
30,26 |
+15,74 |
-1,21 |
8 |
+0,080 |
+15,71 |
30,00 |
-1,07 |
0,88 |
|
11 |
31,17 |
+11,69 |
-0,41 |
9 |
+ 0,094 |
+11,98 |
31,18 |
-1,60 |
±0,77 |
|
12 |
30,07 |
+5,39 |
+0,53 |
10 |
-0,051 |
+5,53 |
30,58 |
-2,59 |
0,88 |
Динамическая модель, записанная в вышеуказанных обозначениях и принятых в (1) основной части, имеет вид
x k = φx k -1 + βu k + yw k . (1)
В данной модели
выделяется составляющая x 0 путем замены x k ,
u k их центрированными
значениями ![]()
![]() , где
, где ![]() и - средние величины перемещения и
температуры воздуха на годичном интервале, взятом за период основания прогноза.
Такой прием повышает обусловленность нормальных уравнений, решаемых для
оценивания параметров, и упрощает вычисления.
и - средние величины перемещения и
температуры воздуха на годичном интервале, взятом за период основания прогноза.
Такой прием повышает обусловленность нормальных уравнений, решаемых для
оценивания параметров, и упрощает вычисления.
В. результате минимизации функционала (7) основной части получают следующую систему нормальных уравнений для оценивания параметров φ и β:
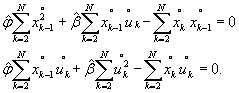 (2)
(2)
После
нахождения из (2) значений ![]() и
и ![]() вычисляют х 0 :
вычисляют х 0 :
![]() (3)
(3)
В рассматриваемом примере система (2) получила значение
![]()
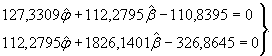
Решив данную
систему уравнений, получим ![]() = 0,7535,
= 0,7535, ![]() = 0,1327, а затем по
(3) находим х 0 = 6,40 мм.
= 0,1327, а затем по
(3) находим х 0 = 6,40 мм.
После
определения ![]() вычисляются остаточные
ошибки:
вычисляются остаточные
ошибки:
![]() (4)
(4)
где x k - фактические значения
перемещения на периоде основания прогноза; ![]() - соответствующие результаты
одношагового прогноза, т. е. прогноза, выполняемого на каждом шаге от
фактического значения перемещения предыдущего цикла наблюдений.
- соответствующие результаты
одношагового прогноза, т. е. прогноза, выполняемого на каждом шаге от
фактического значения перемещения предыдущего цикла наблюдений.
Остаточные
ошибки удобнее вычислять по центрированным значениям ![]() ;
; ![]() ; в этом
случае отпадает необходимость учитывать х0, т. е. прогнозы
вычисляются по формуле
; в этом
случае отпадает необходимость учитывать х0, т. е. прогнозы
вычисляются по формуле
![]() (5)
(5)
а в (4) вместо x k берется ![]() . Результаты
счета ε k даны в таблице.
. Результаты
счета ε k даны в таблице.
Далее по остаточным ошибкам вычисляются согласно (6) основной части значения корреляционной функции
![]()
Временные сдвиги m и вычисленные значения корреляционной функции показаны в таблице. По значениям k ε [ m ] строится график корреляционной функции. Если этот график асимптотически монотонно приближается к оси времени, то описание шумовой компоненты следует выполнять моделью AP 1 (2) основной части. В случае, когда асимптотическое приближение графика корреляционной функции к оси времени проходит колебательно около этой оси, описание шумовой компоненты должно производиться моделью АР2 (3) основной части. Корреляционная функция, незначительно и случайно колеблющаяся около оси времени, представляет белый шум, для которого не следует строить модель шумовой компоненты.
Характер изменения вычисленных в рассматриваемом примере значений корреляционной функции показывает, что шумовую компоненту следует описывать моделью АР2, т. е. уравнением (3) основной части:
w k = μw k -1 + ηw k -2 + ξ k .
В результате минимизации функционала аналогично (8) основной части получают следующие нормальные уравнения для оценивания параметров μ, η, γ :
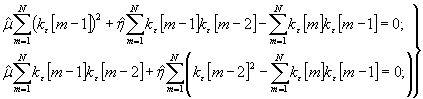 (6)
(6)
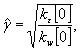 (7)
(7)
где
![]()
Необходимо отметить, что при составлении нормальных уравнений следует подставлять вместо образующихся значений k e [- 1] равные им симметричные значения k ε [1]. Система уравнений (6) получила такое значение:
![]()
Решение такой системы уравнений дает ![]() = -0,2127;
= -0,2127; ![]() = +0,3367, а
дальнейшее вычисление по (7) дает
= +0,3367, а
дальнейшее вычисление по (7) дает ![]() = 0,7708.
= 0,7708.
Таким образом, получены все оценки параметров строящейся модели, и она выражается в следующем виде:
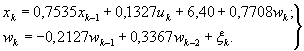 (8)
(8)
По аналогии с (13), (14) основной части алгоритм прогнозной модели имеет следующий вид:
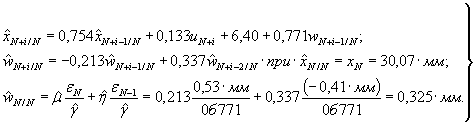 (9)
(9)
![]() ( 10)
( 10)
при
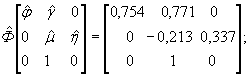
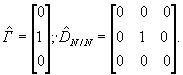
В таблице
показаны результаты краткосрочного прогнозирования x k / k -1 , выполненного
согласно (9) с двушаговым периодом упреждения по приведенным там же значениям
среднемесячной температуры воздуха u k за 1977 г., сдвинутой на величину транспортного
запаздывания. Двушаговый характер прогнозов определялся величиной транспортного
запаздывания, позволяющего получать прогнозы на два месяца вперед по фактическим
значениям входного воздействия. В таблице приведены фактические ошибки
прогнозов Δ k и точность прогнозов, предвычисленная на каждые два шага по
(10) в виде средней квадратической погрешности ![]() Ошибки прогноза лишь в 2 случаях из 12
оказались близкими к значению
Ошибки прогноза лишь в 2 случаях из 12
оказались близкими к значению ![]() а в остальных случаях
укладываются в коридор погрешностей, равный
а в остальных случаях
укладываются в коридор погрешностей, равный ![]() Значительные ошибки прогнозов
обусловлены тем, что в модели используется лишь одно основное входное
воздействие.
Значительные ошибки прогнозов
обусловлены тем, что в модели используется лишь одно основное входное
воздействие.
Приложение 4
ПРИМЕР ИСПОЛЬЗОВАНИЯ ТАБЛИЦ
ДЛЯ НАХОЖДЕНИЯ КРАТКОСРОЧНОГО ПРОГНОЗА
И ОЦЕНКИ ЕГО ТОЧНОСТИ
Таблицы составлены по периоду основания прогноза, охватывающему результаты наблюдений за горизонтальным перемещением гребня плотины Красноярской ГЭС на секции № 22 в промежуток времени с января 1976 г. по декабрь 1980 г. Для построения табл. 1 использовалась динамическая модель, отражающая среднюю зависимость перемещения и гидростатического напора от температуры воздуха и календарного месяца.
Из этой таблицы
выбираются по значению температуры воздуха предварительные значения перемещения
![]() и напора
и напора ![]()
В силу климатических особенностей каждого года и режима работы ГЭС фактические значения напора H ф и перемещения
Таблица 1
|
Температура воздуха, °С |
Гидростатический напор, Перемещения |
||
|
Месяцы |
|||
|
3 |
4 |
5 |
|
|
-11,5 |
86,58 25,19 |
85,52 23,26 |
84,54 20,97 |
|
-11,0 |
86,74 25,26 |
85,68 28,33 |
84,70 21,03 |
x ф отличались на периоде основания
прогноза от представленных в табл. 1. Поэтому строилась вторая динамическая
модель, отражающая зависимость значений ![]() по календарным
месяцам. Кроме того, строилась третья модель в виде авторегрессии, отражающая
влияние на перемещение всех неучтенных в предшествующих моделях факторов. По результатам
экспериментирования с двумя последними моделями составлена табл. 2, из которой по значениям
Δ H выбираются на соответствующий месяц оценки
по календарным
месяцам. Кроме того, строилась третья модель в виде авторегрессии, отражающая
влияние на перемещение всех неучтенных в предшествующих моделях факторов. По результатам
экспериментирования с двумя последними моделями составлена табл. 2, из которой по значениям
Δ H выбираются на соответствующий месяц оценки ![]() Внизу табл. 2
приведены коэффициент α t для вычисления поправки
Внизу табл. 2
приведены коэффициент α t для вычисления поправки ![]() на начало года и
коридор предвычисленных погрешностей δ x ( t ). Таблицы составлены по
моделям с введенным транспортным запаздыванием, равным двум месяцам.
на начало года и
коридор предвычисленных погрешностей δ x ( t ). Таблицы составлены по
моделям с введенным транспортным запаздыванием, равным двум месяцам.
Таблица 2
|
ΔH, м |
Приращение Δ x , мм |
||
|
Месяцы |
|||
|
3 |
4 |
5 |
|
|
0,6 |
0,29 |
0,05 |
0,72 |
|
0,7 |
0,32 |
0,08 |
0,76 |
|
- |
- |
- |
- |
|
α t |
0,590 |
0,495 |
0,416 |
|
δ x ( t ), мм |
1,24 |
1,29 |
1,32 |
Выбранный порядок и структура построения моделей для расчета таблиц позволили избежать отрицательного влияния на устойчивость моделей взаимной корреляции основных входных воздействий - температуры воздуха и гидростатического напора. Введенное транспортное запаздывание дало возможность выполнять краткосрочное прогнозирование по фактическим значениям входных воздействий, измеренным за 2 месяца до прогнозируемого перемещения.
Например,
требуется найти прогноз горизонтального перемещения гребня плотины на 15 апреля
1983 г. (число 15 - средняя дата ежемесячных наблюдений перемещения).
Определяем с учетом транспортного запаздывания средние температуры воздуха и
напора по результатам ежесуточных наблюдений в период с 15 января по 15 февраля
1983 г (при построении модели значения входных воздействий осреднялись между
датами геодезических наблюдений). Они получались равными соответственно-
11,28°С и 84,94 м, Из табл. 1 выбираем, интерполируя на - 11,3°С для 4-го
месяца, значения ![]() = 85,62 м,
= 85,62 м, ![]() = 23,30 мм. Вычисляем ΔН
= 84,94 - 85,62 = -0,68 м, а затем находим в табл. 2 по ΔН
на 4-й месяц значение Δ x = -0,07 мм. Для вычисления
= 23,30 мм. Вычисляем ΔН
= 84,94 - 85,62 = -0,68 м, а затем находим в табл. 2 по ΔН
на 4-й месяц значение Δ x = -0,07 мм. Для вычисления ![]() берется из табл. 2 на
4-й месяц коэффициент α t = 0,495 и умножается на
разность значений перемещений, наблюдавшихся в декабре 1982 г. и в конце
периода основания прогноза:
берется из табл. 2 на
4-й месяц коэффициент α t = 0,495 и умножается на
разность значений перемещений, наблюдавшихся в декабре 1982 г. и в конце
периода основания прогноза: ![]() = 0,495×(31,11 - 29,80) = 0,65
мм. Таким образом, получим значение прогноза:
= 0,495×(31,11 - 29,80) = 0,65
мм. Таким образом, получим значение прогноза: ![]() мм. Фактическое перемещение на 15 февраля 1983 г. равно 24,41
мм, т. е. ошибка прогноза составила Δ = -0,53 мм, точность прогноза
характеризуется σ x ( t ) = ±1,29 мм.
мм. Фактическое перемещение на 15 февраля 1983 г. равно 24,41
мм, т. е. ошибка прогноза составила Δ = -0,53 мм, точность прогноза
характеризуется σ x ( t ) = ±1,29 мм.
Приложение 5
ОПИСАНИЕ КОМПЛЕКСА ПРОГРАММ ПРОГНОЗИРОВАНИЯ ДЕФОРМАЦИЙ
ОБЩИЕ СВЕДЕНИЯ
1. Программы предназначены для обработки результатов уравнивания измерений в геодезических сетях, создаваемых для наблюдений за динамическими процессами перемещений участков земной коры, бетонных плотин ГЭС и других инженерных сооружений и технологического оборудования, а также для построения моделей прогнозирования перемещений пунктов/реперов сети. Функционирование программ обеспечивается при наличии в сети до 100 пунктов/реперов и 5 - 100 циклов измерений.
2. Обозначения и наименование программ:
OSVI 01 - «Программа прогнозирования деформаций по кинематической модели»;
OSVI 02 - «Программа прогнозирования деформаций по динамическим моделям».
Программы написаны на языке ФОРТРАН IV . Для их функционирования необходимы операционная система ОС ЕС (версия 6.1); одна из моделей ЕС ЭВМ с объемом оперативной памяти не менее 512 К; перфокарточное устройство ввода любого типа; печатающее устройство, обеспечивающее построечную печать с длиною строки не менее 120 символов; консоль любого типа (пишущая машинка или дисплей).
3. В алгоритмах программ использованы следующие методы: а) при группировании исходных данных использованы методы математической статистики (Уилкс С. Математическая статистика. - М.: Наука, 1967);
б) для аппроксимации параметров нелинейного тренда использован модифицированный последовательный симплексный метод (Горский В.Г., Адлер Ю.П. Планирование промышленных экспериментов. - М: Металлургия, 1974);
в) при вычислении оценок коэффициентов динамической и кинематической моделей использован метод наименьших квадратов (Линник Ю. В. Метод наименьших квадратов и основы теории обработки наблюдений. - М.: Физматгиз, 1962);
г) расчет прогноза перемещений пунктов/реперов выполнен на основе метода условного среднего (Гуляева Ю. П. Методология прогнозирования деформаций сооружений по геодезическим данным//Геодезия и картография. - 1980. - № 9. - С. 23- 26);
д) оценка параметров и прогноз шумовой составляющей выполнены в соответствии с теорией временных рядов (Бокс Дж., Дженкинс Г. Анализ временных рядов. Прогноз и управление. Вып. 1, 2. - М.: Мир, 1974).
АЛГОРИТМЫ ПРОГРАММ
Алгоритм выделения однородных групп пунктов/ pe п epo в
4. В основе алгоритма группирования пунктов/реперов лежит предположение о том, что отсчеты функции перемещений i -го пункта x i ( t j ), j = l , N принадлежат нормальной генеральной совокупности со средним m x ( t j ) и корреляционной матрицей k x ( t j , t k ), j = 1, N ; k x = l , N . Моментные функции m x ( t j ) и k x ( t j , t k ) заменяются оценками, найденными по n реализациям функций перемещений, принадлежащим однородной группе:
![]() ,
(1)
,
(1)
![]() (2)
(2)
Для выяснения, принадлежит ли l -й пункт с функцией перемещения X l ( t j ) той же генеральной совокупности, рассчитывается обобщенное расстояние Махалонобиса между двумя выборками с объемами n 1 = n и n 2 = 1.. Расстояние D l определяется соотношением
![]() (3)
(3)
где
![]()
![]()
![]()
Статистика
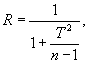 (4)
(4)
где величина T 2
Хоттелинга
определяется как ![]() подчиняется B -распределению
подчиняется B -распределению
![]() , ( N < n )
Решение о принадлежности l -го пункта той же
генеральной совокупности, что и пункты с номерами 1, 2, ..., n , принимается, если функции B -распределения F B ( y )
= P { R ≤ y } для у = Rl будет больше выбранного
уровня значимости α.
, ( N < n )
Решение о принадлежности l -го пункта той же
генеральной совокупности, что и пункты с номерами 1, 2, ..., n , принимается, если функции B -распределения F B ( y )
= P { R ≤ y } для у = Rl будет больше выбранного
уровня значимости α.
Процесс формирования однородных групп состоит из последовательной проверки функций перемещений всех пунктов и выделения из совокупности резко отличающихся (в смысле описанного выше критерия) реализаций. Оставшаяся совокупность образует однородную группу пунктов. Выделенные реализации вновь подвергаются анализу на однородность.
В целях сокращения объема вычислений обращение корреляционной матрицы К х выполняется один раз для каждой группы пунктов. Последующая корректировка обратной матрицы Кх-1 при удалении отдельной реализации выполняется на основе леммы об обратных матрицах
![]() (5)
(5)
где A - вектор-столбец.
Выделение однородных групп пунктов/реперов по данному алгоритму осуществляется только в случае, когда количество временных сечений меньше количества пунктов/реперов, в противном случае группирование должно быть выполнено до начала работы программ.
Алгоритмы построения динамических моделей и вычисления по ним прогноза перемещений
5. Программой OSVI 02 предусмотрена возможность прогнозирования процесса перемещений с использованием линейных динамических моделей 1-го и 2-го порядков, двузвеньевой динамической модели и нелинейной динамической модели, дополненных моделями шумовой компоненты 1-го и 2-го порядков.
Динамические модели процесса перемещений 1-го и 2-го порядков, а также нелинейная динамическая модель представляют собой дискретные динамические модели с расширенным за счет шумовой компоненты вектором состояния. Указанные динамические модели строятся на основе рекуррентного уравнения 1-го и 2-го порядков для одной реализации или для совокупности реализаций процесса перемещений при различном (не более 5) числе входных воздействий. В матричной форме динамическая модель имеет следующий вид:
X k = ФХ k -1 + BU k + Г ξk , (6)
где X k - вектор состояния; U k - вектор управляющих воздействий; ξ k - вектор белого шума.
Матрицы Ф, В, Г содержат искомые параметры динамической модели, причем матрица Ф для нелинейной динамической модели изменяется на каждом шаге. Для разных вариантов моделей процесса перемещений и шума матрицы имеют следующий вид:
а) модель процесса перемещений 1-го порядка, модель шумовой составляющей:
1-го порядка:
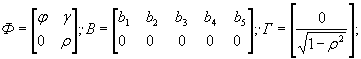 (7)
(7)
2-го порядка:
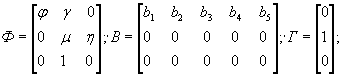 (8)
(8)
б) модель процесса перемещений 2-го порядка, модель шумовой составляющей:
1-го порядка:
![]()
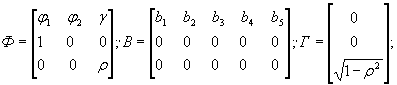 (9)
(9)
2-го порядка:
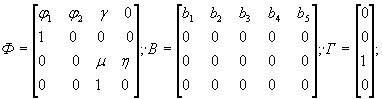 (10)
(10)
в) нелинейная модель процесса перемещения, модель шумовой составляющей:
1-го порядка:
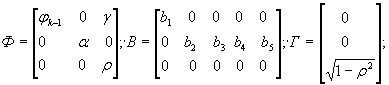 (11)
(11)
2-го порядка:
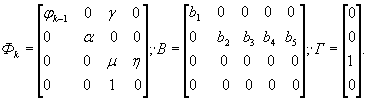 (12)
(12)
Двузвеньевая динамическая модель процесса перемещений представляет собой континуальную модель, построенную на основе дифференциального уравнения второго порядка, дополненного шумовой компонентой. В матричной форме модель имеет следующий вид:
![]() (13)
(13)
где X ( t ), U ( t ), W ( t ) - соответственно вектор состояния, вектор управляющих воздействий и вектор шума на момент времени t . Матрицы Ф, В, Г содержат искомые параметры двузвеньевой динамической модели.
Для линейных динамических моделей 1-го и 2-го порядков программой предусмотрено два возможных варианта порядка оценивания параметров модели:
1) на первом шаге по математическому ожиданию процесса перемещения оцениваются параметры φ, φ1, φ2, b i , i = 1,5; на втором шаге по остаточным ошибкам оцениваются параметры ρ , γ , μ , η ;
2) на первом шаге по корреляционной функции процесса перемещений оцениваются параметры φ, φ1, φ2, на втором шаге по математическому ожиданию процесса перемещений - параметры b i , i = 1,5 и только после этого по остаточным ошибкам оцениваются параметры ρ , γ , μ , η .
Оценивание параметров модели выполняется методом наименьших квадратов.
Построение двузвеньевой и нелинейной динамических моделей программой выполняется в единственном варианте. На первом шаге модифицированным симплекс-методом по математическому ожиданию процесса перемещений оцениваются параметры, описывающие динамические свойства системы и степень влияния управляющих воздействий. На втором шаге методом наименьших квадратов по остаточным ошибкам оцениваются параметры, описывающие шумовую составляющую процесса перемещений.
После оценивания параметров получают динамическую модель процесса перемещений наблюдаемых точек сооружения в виде уравнения условного математического ожидания, которое и является прогнозной моделью. Особенность двузвеньевой динамической модели заключается в том, что программой предусмотрена на этапе прогнозирования дискретизация непрерывной модели с постоянным шагом по времени Δ t . Таким образом, на этапе прогнозирования двузвеньевая динамическая модель описывается уравнением (6), где соответствующие матрицы имеют вид:
при шумовой составляющей, описываемой моделью 1-го порядка
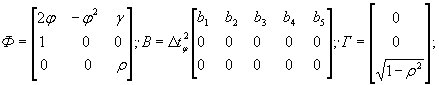 (14)
(14)
при шумовой составляющей, описываемой моделью 2-го порядка
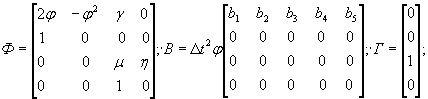 (15)
(15)
причем
φ = exp ( α Δt ), (16)
где α - параметр, описывающий динамические свойства двузвеньевой модели и оцененный на этапе построения модели; Δ t - дискрет времени.
Точность результатов прогнозирования выражается через дисперсию
![]() (17)
(17)
где N - номер последнего цикла основания прогноза; N + i - номер цикла, для которого вычисляется дисперсия ( i = 1, 2...).
Начальное
условие: ![]() Dn / n = ГГТ.
Dn / n = ГГТ.
Алгоритм анализа нормальности
случайной функции процесса перемещений
6. Проверка нормальности распределения случайной функции перемещений x ( t ) выполняется по оценке ее числовых характеристик: асимметрии и эксцессу. Вычисляются следующие характеристики:
а) оценка математического ожидания
![]() (18)
(18)
б) оценка центрального момента k -то порядка ( k = 2, 3, 4)
![]() (19)
(19)
в) оценка среднего квадратического отклонения
![]() (20)
(20)
г) оценка асимметрии
![]() (21)
(21)
д) оценка эксцесса
![]() (22)
(22)
Гипотеза о нормальности распределения реализаций перемещений в каждом временном сечении принимается как не противоречащая эмпирическим данным, если соблюдаются неравенства:
 (23)
(23)
где
![]()
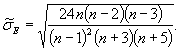
Если гипотеза не принимается для отдельных временных сечений, то эти сечения исключаются из рассмотрения. Если гипотеза не принимается для всех рассматриваемых сечений, то выполняется нормализующее преобразование: при асимметрии отрицательной - экспоненциальное, при асимметрии положительной- логарифмическое.
Алгоритм построения кинематической модели и вычисления по ней прогноза перемещений
7. Полный алгоритм кинематической модели включает в себя следующие этапы: выделение нелинейного тренда, оценку параметров кинематической модели и расчет прогноза процесса перемещений.
В программе предусмотрена аппроксимация тренда линейной функцией, экспонентой и синусоидой:
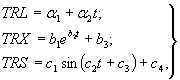 (24)
(24)
где α i ( i = 1, 2), b i ( i = 1, 3), c i ( i = 1, 4) - оцениваемые коэф фициенты соответственно линейного, экспоненциального и синусоидального трендов; t - время.
Оценка параметров тренда выполняется модифицированным симплекс-методом. Решение о наличии в исходных данных тренда того или иного вида принимается на основе сравнения значений остаточного функционала (суммы квадратов отклонений наблюдаемых величин от аппроксимирующей кривой) для каждой из трех функций (24). При наличии нелинейного тренда выполняется центрирование процесса. Для центрированного процесса перемещения, а также при наличии в исходных данных линейного тренда для любой i -й реализации прогнозная кинематическая модель записывается в виде уравнений условного математического ожидания и условного среднего квадратического отклонения:
![]() (25)
(25)
![]() (26)
(26)
где t 1 , t 2 -
соответственно время конца периода основания прогноза и цикла, для которого
вычисляется прогноз; ![]() - прогнозная оценка
значения перемещения i - ro знака
(марки) при его исходном значении в конце периода основания прогноза, равном
- прогнозная оценка
значения перемещения i - ro знака
(марки) при его исходном значении в конце периода основания прогноза, равном ![]()
![]() - оценка
математического ожидания процесса перемещения в момент времени t ;
- оценка
математического ожидания процесса перемещения в момент времени t ; ![]() - среднее квадратическое отклонение;
- среднее квадратическое отклонение; ![]() - коэффициент корреляции.
- коэффициент корреляции.
Оценка параметров кинематической модели выполняется путем аппроксимации соответствующих статистических оценок, полученных для сечений процесса перемещений на периоде основания прогноза. В качестве аппроксимирующих функций в программе используются следующие выражения:
![]() (27)
(27)
![]() (28)
(28)
![]() (29)
(29)
где α , b , с , d , k - коэффициенты аппроксимирующих функций, вычисляемые по способу наименьших квадратов; n ≥ m - номера циклов наблюдений на периоде основания прогноза.
Теснота зависимости между оценками параметров кинематической модели и аппроксимирующими кривыми характеризуется корреляционными отношениями, вычисляемыми по известным формулам.
Прогноз перемещения i -й марки выполняется следующим образом. По уравнениям
(27)...(29) определяют путем экстраполяции оценки ![]()
![]()
![]() и, подставляя их совместно с
и, подставляя их совместно с ![]() ,
, ![]()
![]() в уравнения (25) и
(26), получают прогноз i -г o значения перемещения
в уравнения (25) и
(26), получают прогноз i -г o значения перемещения ![]() и характеристику прогноза
и характеристику прогноза ![]()
Если при построении кинематической модели
исключался нелинейный тренд, прогнозное значение перемещения i -й марки находится путем суммирования оценки ![]() со значением тренда в момент времени t 2 . В случае
нормализующего преобразования исходных данных выполняется преобразование
прогнозных значений перемещений, обратное нормализующему.
со значением тренда в момент времени t 2 . В случае
нормализующего преобразования исходных данных выполняется преобразование
прогнозных значений перемещений, обратное нормализующему.
ВХОДНЫЕ ДАННЫЕ
Предварительная подготовка входных данных
8. Входные данные в программах OSVI 01 и OSVI 02 разделены на основные входные данные и исходные данные управления режимами.
Основные входные данные содержат уравненные результаты геодезических наблюдений и до начала работы должны быть записаны в библиотеку исходных модулей, например, с именем KRASTX , в раздел DANN . Исходные данные управления режимами вводятся с перфокарточного устройства в процессе работы программы.
Описание основных входных данных, записываемых в раздел DANN библиотеки исходных модулей с именем KRASTX
9. UP - параметр управления печатью, UP = 1 - полная печать результатов, UP = 0 - печать только результатов прогнозирования;
N - число пунктов/реперов;
М - число циклов наблюдений, при прогнозировании по динамическим моделям, включая циклы, для которых выполняется прогнозирование;
FOR - формат для ввода результатов геодезических наблюдений;
А - одномерный массив результатов геодезических наблюдений размером N >|< M , вводится последовательно строка за строкой, причем строка соответствует результатам геодезических наблюдений за перемещениями i -г o пункта/репера, т.е. i -й реализации перемещений. При прогнозировании по динамическим моделям для циклов на периоде упреждения прогноза можно принять нулевые значения перемещений;
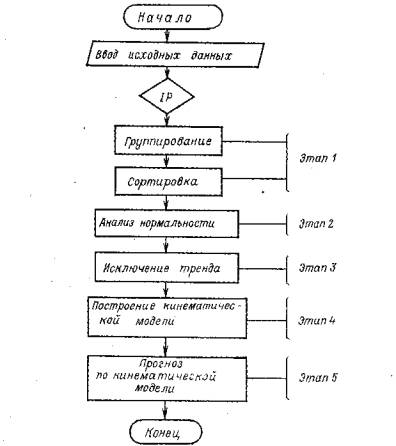
Рис. 1.
FOR - формат для ввода вектора моментов времени циклов наблюдений;
Т - вектор моментов времени циклов наблюдений длиной М;
IP - вектор признаков длиной 5 для программы OSVI 01 и длиной 3 для программы OSVI 02, IP ( I ) = 1 - 1-й этап программы выполняется, I Р(1)=0 - 1-й этап не выполняется. Схема программы OS , VI 01 с содержанием выполняемых вычислений по этапам приведена на рис. 1, программы OSVI 02 - на рис. 2. Возможные варианты задания вектора признаков для программы OSVI 01 приведены в табл. 1 и для программы OSVI 02 – в табл. 2.
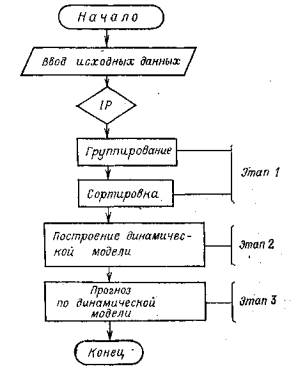
Рис. 2.
Таблица 1
|
Номер варианта |
Значение IP |
Выполняемые этапы |
||||||||
|
1 |
1 |
1 |
1 |
1 |
1 |
1, |
2, |
3, |
4, |
5 |
|
2 |
0 |
1 |
1 |
1 |
1 |
2, |
3, |
4 |
5 |
|
|
3 |
1 |
1 |
1 |
1 |
0 |
1, |
2, |
3, |
4 |
|
|
4 |
0 |
1 |
1 |
1 |
0 |
2, |
3, |
4 |
|
|
|
5 |
1 |
1 |
1 |
0 |
0 |
1, |
2, |
3 |
|
|
|
6 |
1 |
1 |
0 |
0 |
0 |
2, |
3 |
|
|
|
|
7 |
1 |
1 |
0 |
0 |
0 |
1, |
2 |
|
|
|
|
8 |
0 |
1 |
0 |
0 |
0 |
|
2 |
|
|
|
Таблица 2
|
Номер варианта |
Значение IP |
Выполняемые этапы |
||||
|
1 |
1 |
0 |
0 |
1 |
|
|
|
2 |
1 |
1 |
0 |
1, |
2 |
|
|
3 |
0 |
1 |
0 |
2 |
|
|
|
4 |
1 |
1 |
1 |
1, |
2, |
3 |
|
5 |
0 |
1 |
1 |
2, |
3 |
|
Другие варианты выполнения этапов в программах не предусмотрены.
Исходные данные управления режимами для программы OSVI 01.
Ввод с перфокарточного устройства
Исходные данные управления режимами вводятся по ходу выполнения расчетов в ответ на сообщения программы.
В случае, если i -й этап программы не выполняется, соответствующие ему исходные данные управления режимами не вводятся.
Этап 1. Группирование данных
ALF - уровень значимости при группировании данных;
KG - код продолжения, принимающий на этапе группирования исходных данных следующие значения: KG = 1 - ввести другое значение уровня значимости и повторить группирование; KG = 2 - дальнейшее выполнение программы; KG = 3 - конец программы; KG = 0 - переход к ручному группированию.
В случае отказа от выполнения 1-го этапа, т. е. IP ( I ) = 0, либо при переходе на 1-м этапе к ручному группированию вводятся следующие исходные данные:
NGR - число групп реализаций;
NR 1- вектор количества пунктов/реперов в группах длиной NGR ;
NR 2 - вектор номеров групп каждой реализации длиной N.
Этап 2. Анализ нормальности
NR (1)- число интервалов разбиения выборки при анализе нормальности распределения данных.
Этап 3. Исключение тренда
Е - точность аппроксимации нелинейного тренда;
KG - код продолжения, принимающий на этапе аппроксимации тренда следующие значения: KG < 0 - переход к обработке следующей группы наблюдений; KG = 0 - продолжение расчета; KG > 0 - повторить аппроксимацию нелинейного тренда с тем же значением точности аппроксимации.
Этап 4. Построение кинематической модели
Исходные данные управления режимами на этапе построения кинематической модели не требуются.
Этап 5. Прогноз по кинематической модели
NR - вектор параметров расчета прогноза по кинематической модели, длина вектора 4: NR (1) - число циклов контрольного прогноза; NR (3) - число циклов для прогноза за пределами интервала наблюдений; NR (4) - номер последнего цикла наблюдений на периоде основания прогноза;
DT - дискрет времени для прогноза за пределами интервала наблюдения;
KG - код продолжения: KG = 1- продолжить расчет для следующей группы марок; KG ≠ 1 - конец программы.
Исходные данные управления режимами для программы OSVI 02.
Ввод с перфокарточного устройства
11. Условия ввода исходных данных управления режимами для программы OSVI 02 такие же, как и для программы OSVI 01 (см. п. 10).
Этап 1. Группирование данных
Исходные данные аналогичны исходным данным этапа 1 для программы OSVI 01.
Этап 2. Построение динамической модели
NR - вектор размерностей динамической модели, длина вектора 5.
NR (1) - порядок оценивания параметров модели процесса перемещений: NR (1)=0 - оценивание по среднему; NR (1) = 1- оценивание по корреляционной функции;
NR (2) - размерность модели перемещений: NR (2) =0 - комплексная модель 1-го порядка; NR (2) = 1 - комплексная модель 2-го порядка; NR (2) =2 - двузвеньевая модель; NR (2) =3 - нелинейная модель;
NR (3) - размерность модели шума: NR (3) = 1 - модель шума 1-го порядка; NR (3) = 2 - модель шума 2-го порядка;
NR (4) - число временных сечений для построения модели;
NR (5) - число управляющих воздействий, не более 5;
FOR - формат для ввода управляющих воздействий;
R 22 - одномерный массив управляющих воздействий размером NR (5)>|< M , вводится последовательно строка за строкой, причем строка соответствует значениям i -го управляющего воздействия от первого цикла на периоде основания прогноза до последнего цикла на периоде упреждения прогноза;
Е - точность вычисления параметров двузвеньевой и нелинейной моделей, при построении комплексных моделей следует ввести любое число, например, Е = 0;
ВВ(1) - начальное значение коэффициента динамики нелинейной модели. При отказе от задания коэффициента динамики, определенного предварительным расчетом как для линейной модели (см. п. 4.16) ввести ВВ(1) = -999, в этом случае программой автоматически задается ВВ(1) = 0,7. При построении комплексных и двузвеньевой моделей ВВ(1) не вводится;
KG - код продолжения, принимающий на этапе построения двузвеньевой и нелинейной моделей следующие значения: KG = 0 - конец программы; KG = 1 - переход к обработке следующей группы марок; KG = 2 - продолжить расчет; KG = 3 - повторить вычисление параметров двузвеньевой и нелинейной моделей с дру гим значением точности; KG = 4 - продолжить аппроксимацию параметров двузвеньевой и нелинейной моделей с тем же значением точности. При построении комплексных моделей код продолжения на этапе 2 не вводится.
Этап 3. Построение прогноза по динамической модели
KG - код продолжения: KG = 1 - перейти к обработке следующей группы марок; KG ≠ 1 - конец программы.
ВЫХОДНЫЕ ДАННЫЕ
Характер и организация выходных данных
12. Результаты вычислений выводятся на печать через АЦПУ. В программе предусмотрены два варианта печати: полный и сокращенный. При полной печати выводятся все результаты вычислений, при сокращенной печати - только результаты прогноза перемещений. Входные данные выводятся на АЦПУ при обоих вариантах печати в форматах ввода. Сообщения программ о ходе выполнения расчетов выводятся на консоль.
Выходные данные» программы OSVI01
13. В табл. 3 приведены результаты, выводимые на печать, и соответствующие им форматы. В графе « UP » цифра 1 означает «полная печать», 0 - «сокращенная печать».
Таблица 3
|
Этап |
Результат |
Формат |
UP |
|
1 |
NGR - число однородных групп |
I 3 |
1 |
|
ALF - уровень значимости |
Е 12.5 |
1 |
|
|
NR 1 - массив чисел марок в группах длиной NGR |
I 3 |
1 |
|
|
R 20 - отсортированный массив наблюдений |
Е 12.5 |
1 |
|
|
IND - массив старых номеров строк матрицы А наблюдений |
I 3 |
1 |
|
|
2 |
КСН - количество неисключенных циклов |
I 3 |
1 |
|
К2 - тип нормализующего преобразования |
Текст сообщения |
1 |
|
|
А2 - константа сдвига |
Е 12.5 |
1 |
|
|
R 21- массив признаков исключенных циклов |
Е 12.5 |
1 |
|
|
3 |
NH - число шагов аппроксимации |
I 2 |
1 |
|
Е - точность аппроксимации |
Е 12.5 |
1 |
|
|
NR (1) - тип нелинейного тренда |
Текст сообщения |
1 |
|
|
R 12 - коэффициенты экспоненциального тренда |
Е 12.5 |
1 |
|
|
R 11 - коэффициенты синусоидального тренда |
Е 12.5 |
1 |
|
|
А - массив наблюдений после исключения тренда |
Е 12.5 |
1 |
|
|
4 |
R 13 - массив параметров кинематической модели |
Е 12.5 |
1 |
Продолжение таблицы 3
|
Этап |
Результат |
Формат |
UP |
|
5 |
NR - массив параметров прогноза перемещений |
I 3 |
0,1 |
|
DT - дискрет времени для прогноза за пределами интервала наблюдений |
Е 5.0 |
0,1 |
|
|
А - массив результатов прогноза перемещений |
Е 12.5 |
0,1 |
|
|
R 21 - массив верхних границ доверительного интервала |
Е 12.5 |
0,1 |
|
|
R 22 - массив нижних границ доверительного интервала |
Е 12.5 |
0,1 |
Выходные данные программы OSVI 02
14. Выходные данные приведены в табл. 4, 0 и 1 в графе « UP » означают, как и выше, соответственно «сокращенная печать» и «полная печать».
Таблица 4
|
Этап |
Результат |
Формат |
UP |
|
1 |
Результаты аналогичны результатам программы OSVI 01 на этапе I |
|
1 |
|
2 |
KLUCH - признак достижения точности аппроксимации параметров двузвеньевой или нелинейной моделей |
Текст сообщения |
0,1 |
|
ВВ - вектор параметров двузвеньевой или нелинейной моделей после аппроксимации |
Е 12.5 |
0,1 |
|
|
FQ - остаточный функционал |
Е 12.5 |
0,1 |
|
|
NR - вектор размерностей динамической модели |
I 2 |
1 |
|
|
NR (7) - признак устойчивости модели |
Текст сообщения |
1 |
|
|
R 22 - массив управляющих воздействий |
Е 12.5 |
1 |
|
|
R 12, RO , BZ - параметры модели шума |
Е 12.5 |
1 |
|
|
R 11 - коэффициенты модели перемещений |
Е 12.5 |
1 |
|
|
R 10 - вектор корреляционной функции |
Е12.5 |
1 |
|
|
3 |
NN - номер последнего временного сечения периода основания прогноза |
I 2 |
0,1 |
|
A - массив значений прогноза перемещений |
Е 12.5 |
0,1 |
|
|
R 21 - массив значений прогноза шума |
Е 12.5 |
0,1 |
|
|
R 20 - массив стандартных отклонений прогноза |
Е 12.5 |
0,1 |
Сообщения программы OSVI01
15. Расшифровка сообщений и действия оператора приведены в табл. 5.
Таблица 5
|
Этап |
Текст сообщения |
Действия оператора |
|
|
1 |
Ошибки в карте признаков, замените карту |
Заменить карту признаков IP , ответить U |
|
|
Задайте данные для группирования |
Подготовить на карточном вводе карты для группирования, ответить U |
||
|
Неправильно задано ALF , измените данные |
Заменить карту с ALF ответить U |
|
|
|
Задайте код продолжения, фаза 1 |
Задать код продолжения, ответить U 1 |
||
|
Неправильно задано KG , измените данные |
Заменить карту с KG , ответить U |
|
|
|
2 |
Задайте данные для анализа нормальности распределения |
Подготовить на карточном вводе данные для анализа нормальности распределения, ответить U |
|
|
3 |
Задайте данные для исключения тренда |
Подготовить на карточном вводе данные для исключения тренда, ответить U |
|
|
Задайте код продолжения, фаза 3 |
Задать код продолжения, ответить U 2 |
||
|
4 |
Задайте данные для прогноза перемещений |
Подготовить на карточном вводе данные для вычисления прогноза, ответить U |
|
|
Задайте код продолжения, фаза 5 |
Задать код продолжения, ответить U 3 |
|
1 Проанализировать результаты группирования данных и выбрать соответствующий код продолжения.
2 Проанализировать результаты аппроксимации нелинейного тренда и выбрать код продолжения.
3 Проанализировать результаты расчетов по группе марок и выбрать код продолжения.
Сообщения программы OSVI02
16. Расшифровка сообщений и действия оператора приведены в табл. 6.
Таблица 6
|
Этап |
Текст сообщения |
Действия оператора |
|
1 |
Сообщения программы и действия оператора аналогичны сообщениям программы OSVI 01 на этапе 1 |
|
|
2 |
Задайте данные для динамической модели |
Подготовить на карточном вводе данные для построения динамической модели, ответить U |
Продолжение таблицы 6
|
Этап |
Текст сообщения |
Действия оператора |
|
|
Не достигается точность аппроксимации |
Принять сообщение к сведению, ответить U |
|
Задайте код продолжения, фаза 2 |
Задать код продолжения, ответить U1 |
|
|
Неправильно задано KG, измените данные |
Заменить карту с KG, ответить U |
|
|
3 |
Задайте код продолжения, фаза 3 |
Задать код продолжения, ответить U2 |
1 Проанализировать результаты аппроксимации и выбранное ранее значение точности вычисления (Е) параметров двузвеньевой или нелинейной моделей и выбрать код продолжения. Если выбрано KG = 3, подготовить на карточном вводе карты с KG и новым значением Е, ответить U .
2 Проанализировать результаты расчетов по группе марок и выбрать код продолжения.